\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高一数学同步精品讲义与分层练习(人教A版2019)]
(https://www.zxxk.com/docpack/2921718.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第二册同步巩固,难度2颗星!
基础知识
向量加法的三角形法则
已知向量非零向量\(\vec{a}\), \(\vec{b}\), 在平面内取任意一点\(A\) , 作 \(\overrightarrow{A B}=\vec{a}\) , \(\overrightarrow{B C}=\vec{b}\),则向量 \(\overrightarrow{A C}\)叫做\(\vec{a}\)与\(\vec{b}\)的和,记作\(\vec{a}+\vec{b}\),即 \(\vec{a}+\vec{b}=\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\).
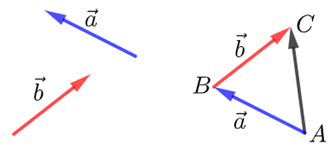
解释
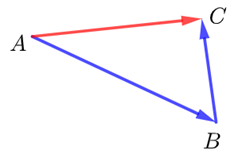
(1) 物理知识告诉我们,质点经过\(\overrightarrow{A B}\),\(\overrightarrow{B C}\)两次位移,相当于从点\(A\)直接到点\(C\)的位移\(\overrightarrow{A C}\)结果相同,位移的合成可以看作向量加法三角形法则的物理模型;

向量加法的平行四边形法则
以同一点\(O\)为起点的两个已知向量\(\vec{a}\), \(\vec{b}\),以\(OA\),\(OB\)为邻边作\(◻OACB\),则以\(O\)为起点的向量 \(\overrightarrow{O C}\)
(\(OC\)是\(◻OACB\)的对角线)就是向量\(\vec{a}\)与\(\vec{b}\)的和.
如下图, \(\overrightarrow{O A}=\vec{a}, \overrightarrow{O B}=\vec{b}\),则\(\vec{a}+\vec{b}=\overrightarrow{O A}+\overrightarrow{O B}=\overrightarrow{O C}\);

我们把这种作两个向量和的方法叫做向量加法的平行四边形法则.
解释
一个物体同时收到两个外力\(\overrightarrow{F_1}\)与\(\overrightarrow{F_2}\)的作用,那如何确定合力\(\overrightarrow{F}\)呢?由物理知识可知,合力\(\overrightarrow{F}\)在以\(OA\),\(OB\)为邻边的平行四边形的对角线上,并且大小等于这条对角线的长. 力的合成可以看作向量加法平行四边形法则的物理模型.

【例】 已知向量\(\vec{a}\), \(\vec{b}\),求作向量\(\vec{a}+\vec{b}\).

解 作法1 如图,在平面内任取一点\(O\),作\(\overrightarrow{O A}=\vec{a}\) , \(\overrightarrow{A B}=\vec{b}\),则\(\overrightarrow{O B}=\vec{a}+\vec{b}\);

作法2 如图,在平面内任取一点\(O\),作\(\overrightarrow{O A}=\vec{a}\) , \(\overrightarrow{A B}=\vec{b}\),以\(OA\),\(OB\)为邻边作\(◻OACB\),连接\(OC\),则 \(\overrightarrow{O C}=\overrightarrow{O A}+\overrightarrow{O B}=\vec{a}+\vec{b}\).

向量三角不等式
一般地 , 我们有
\(|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|\)
当且仅当\(\vec{a}\), \(\vec{b}\)方向相同时等号成立.
解释
当\(\vec{a}\), \(\vec{b}\)不共线时,由三角形三边关系\(AC+BC>AB\),可得 \(|\vec{a}|+|\vec{b}|>|\vec{a}+\vec{b}|\);

当\(\vec{a}\), \(\vec{b}\)反向时, \(|\vec{a}+\vec{b}|=|| \vec{a}|-| \vec{b}||<|\vec{a}|+|\vec{b}|\),
当\(\vec{a}\), \(\vec{b}\)同向时, \(|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|\),
综上 \(|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|\),当且仅当\(\vec{a}\), \(\vec{b}\)方向相同时等号成立.
同理易得 \(|\vec{a}+\vec{b}| \geq|| \vec{a}|-| \vec{b}||\),
故 \(|| \vec{a}|-| \vec{b}|| \leq|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|\).
运算律
向量的加法满足交换律和结合律,即 \(\vec{a}+\vec{b}=\vec{b}+\vec{a},(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})\).
基本方法
【题型1】 向量加法的理解
【典题1】如图,在正六边形\(ABCDEF\)中,\(O\)是其中心.

则① \(\overrightarrow{A B}+\overrightarrow{C D}=\)\(\underline{\quad \quad}\);② \(\overrightarrow{A B}+\overrightarrow{A F}+\overrightarrow{B C}=\)\(\underline{\quad \quad}\);③ \(\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{E F}=\)\(\underline{\quad \quad}\) .
解析 ①\(\overrightarrow{A B}+\overrightarrow{C D}=\overrightarrow{O C}+\overrightarrow{O E}=\overrightarrow{O D}\);
②\(\overrightarrow{A B}+\overrightarrow{A F}+\overrightarrow{B C}=\overrightarrow{A C}+\overrightarrow{A F}=\overrightarrow{A F}+\overrightarrow{F D}=\overrightarrow{A D}\);
③\(\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{E F}=\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{D O}=\overrightarrow{O C}\).
点拨 利用平行四边形法则或三角形法则求向量加法.
【典题2】向量\((\overrightarrow{P A}+\overrightarrow{M A})+(\overrightarrow{A O}+\overrightarrow{A C})+\overrightarrow{O M}\)化简后等于\(\underline{\quad \quad}\).
解析 向量\((\overrightarrow{P A}+\overrightarrow{M A})+(\overrightarrow{A O}+\overrightarrow{A C})+\overrightarrow{O M}=\overrightarrow{P A}+\overrightarrow{M A}+\overrightarrow{A O}+\overrightarrow{O M}+\overrightarrow{A C}=\overrightarrow{P O}+\overrightarrow{A C}=\overrightarrow{P C}\).
点拨 利用首尾相接法.
【典题3】\(O\)是平行四边形\(ABCD\)外一点,求证: \(\overrightarrow{O A}+\overrightarrow{O C}=\overrightarrow{O B}+\overrightarrow{O D}\).

**解析 ** \(\overrightarrow{O A}+\overrightarrow{O C}=\overrightarrow{O B}+\overrightarrow{B A}+\overrightarrow{O D}+\overrightarrow{D C}=(\overrightarrow{O B}+\overrightarrow{O D})+(\overrightarrow{B A}+\overrightarrow{D C})\),
因为\(ABCD\)是平行四边形,所以\(\overrightarrow{B A}+\overrightarrow{D C}=\overrightarrow{0}\),
所以\(\overrightarrow{O A}+\overrightarrow{O C}=\overrightarrow{O B}+\overrightarrow{O D}\).
【巩固练习】
1.在\(△ABC\)中,下列四个结论中正确的是( )
① \(\overrightarrow{A B}+\overrightarrow{B C}>\overrightarrow{A C}\) ② \(\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\) ③ \(|\overrightarrow{A B}|+|\overrightarrow{B C}|>|\overrightarrow{A C}|\) ④ \(|\overrightarrow{A B}|+|\overrightarrow{B C}|=|\overrightarrow{A C}|\).
A.①③ \(\qquad \qquad \qquad \qquad\) B.②③ \(\qquad \qquad \qquad \qquad\) C.①④ \(\qquad \qquad \qquad \qquad\) D.②④
2.在四边形\(ABCD\)中,若 \(\overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{A D}\),则四边形\(ABCD\)的形状一定是( )
A.平行四边形 \(\qquad \qquad \qquad \qquad\) B.菱形 \(\qquad \qquad \qquad \qquad\) C.矩形 \(\qquad \qquad \qquad \qquad\) D.正方形
3.化简 \((\overrightarrow{A B}+\overrightarrow{M B})+(\overrightarrow{B O}+\overrightarrow{B C})+\overrightarrow{O M}=\) .
4.若 \(\vec{a}=\)“向北走\(8 km\)”, \(\vec{b}=\)“向东走\(8 km\)”,则 \(|\vec{a}+\vec{b}|=\) \(\underline{\quad \quad}\) ; \(\vec{a}+\vec{b}\)的方向是\(\underline{\quad \quad}\) .
5.如图所示,中心为\(O\)的正八边形\(A_1 A_2…A_7 A_8\)中, \(\overrightarrow{a_{\imath}}=\overrightarrow{A_{\imath} A_{\imath+1}}(i=1,2, \ldots, 7)\), \(\overrightarrow{b_J}=\overrightarrow{O A_J}(j=1,2, \ldots, 8)\),试化简 \(\overrightarrow{a_2}+\overrightarrow{a_5}+\overrightarrow{b_2}+\overrightarrow{b_5}+\overrightarrow{b_7}\).

参考答案
-
答案 \(B\)
解析 \(\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\);\(∴\)结论②正确;
两边之和大于第三边, \(\therefore|\overrightarrow{A B}|+|\overrightarrow{B C}|>|\overrightarrow{A C}|\);即结论③正确;
\(∴\)结论正确的是②③.
故选:\(B\). -
答案 \(A\)
解析 在四边形ABCD中, \(\because \overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{A D}\),且 \(\overrightarrow{A C}=\overrightarrow{A B}+\overrightarrow{B C}\), \(\therefore \overrightarrow{A D}=\overrightarrow{B C}\);
即\(AD//BC\),且\(AD=BC\),如图所示;
\(∴\)四边形\(ABCD\)是平行四边形.
故选:\(A\).
-
答案 \(\overrightarrow{A C}\)
解析 原式 \(=(\overrightarrow{A B}+\overrightarrow{B O})+(\overrightarrow{O M}+\overrightarrow{M B})+\overrightarrow{B C}=\overrightarrow{A O}+\overrightarrow{O B}+\overrightarrow{B C}=\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\). -
答案 \(8 \sqrt{2}\),东北方向.
解析 由向量加法的平行四边形法则,知\(|\vec{a}+\vec{b}|=8 \sqrt{2}\),方向为东北方向. -
答案 \(\overrightarrow{b_6}\)
解析 因为\(\overrightarrow{a_{\imath}}=\overrightarrow{A_{\imath} A_{\imath+1}}(i=1,2, \ldots, 7)\), \(\overrightarrow{b_J}=\overrightarrow{O A_J}(j=1,2, \ldots, 8)\),
所以\(\overrightarrow{a_2}+\overrightarrow{a_5}+\overrightarrow{b_2}+\overrightarrow{b_5}+\overrightarrow{b_7}=\overrightarrow{A_2 A_3}+\overrightarrow{A_5 A_6}+\overrightarrow{O A_2}+\overrightarrow{O A_5}+\overrightarrow{O A_7}\)\(=\overrightarrow{O A_3}+\overrightarrow{O A_6}+\overrightarrow{O A_7}=\overrightarrow{O A_3}+\overrightarrow{O A_6}-\overrightarrow{O A_3}=\overrightarrow{O A_6}=\overrightarrow{b_6}\).
【题型2】 向量三角不等式
【典题1】 已知向量\(|\vec{a}|=2\), \(|\vec{b}|=8\),则\(|\vec{a}+\vec{b}|\)的最大值是\(\underline{\quad \quad}\) ,最小值是\(\underline{\quad \quad}\).
解析 因为 \(|| \vec{a}|-| \vec{b}|| \leq|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|\),所以 \(6 \leq|\vec{a}+\vec{b}| \leq 10\),
当\(\vec{a}\),\(\vec{b}\)方向相同,\(|\vec{a}+\vec{b}|\)取到最小值\(6\);
当\(\vec{a}\),\(\vec{b}\)方向相反,\(|\vec{a}+\vec{b}|\)取到最大值\(10\).
点拨 向量三角不等式\(|| \vec{a}|-| \vec{b}|| \leq|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|\).
【典题2】对于任意向量\(\vec{a}\),\(\vec{b}\),\(\vec{c}\),下列说法正确的是( )
A. \(|\vec{a}+\vec{b}+\vec{c}| \geqslant|\vec{a}|-|\vec{b}|-|\vec{c}|\)\(\qquad \qquad \qquad \qquad\) B. \(|\vec{a}+\vec{b}+\vec{c}| \geqslant|\vec{a}|+|\vec{b}|-|\vec{c}|\)
C. \(|\vec{a}+\vec{b}+\vec{c}| \geqslant|\vec{a}|+|\vec{b}|\) \(\qquad \qquad \qquad \qquad\) D. \(|\vec{a}+\vec{b}+\vec{c}| \geqslant|\vec{a}|-|\vec{b}|\)
解析 对于\(A\),任意向量\(\vec{a}\),\(\vec{b}\),\(\vec{c}\),都有 \(|\vec{a}+\vec{b}+\vec{c}| \geqslant|\vec{a}+\vec{b}|-|\vec{c}| \geqslant|\vec{a}|-|\vec{b}|-|\vec{c}|\),\(A\)正确;
对于\(B\),当向量\(\vec{a}\),\(\vec{b}\)是非零向量,且互为相反向量,\(\vec{c}=\overrightarrow{0}\)时, \(|\vec{a}+\vec{b}+\vec{c}|<|\vec{a}|+| \vec{b}|-| \vec{c} \mid\),\(B\)错误;
对于\(C\),当向量\(\vec{a}\),\(\vec{b}\)是非零向量,且互为相反向量,\(\vec{c}=\overrightarrow{0}\)时, \(|\vec{a}+\vec{b}+\vec{c}|<|\vec{a}|+|\vec{b}|\),\(C\)错误;
对于\(D\),当向量\(\vec{a}\),\(\vec{c}\)是非零向量,且互为相反向量,\(\vec{b}=\overrightarrow{0}\)时, \(|\vec{a}+\vec{b}+\vec{c}|<|\vec{a}|-|\vec{b}|\),\(D\)错误.
故选:\(A\).
【巩固练习】
1.下列各等式或不等式中,一定不能成立的个数是( )
①\(|\vec{a}|-|\vec{b}|<|\vec{a}+\vec{b}|<|\vec{a}|+|\vec{b}|\);② \(|\vec{a}|-|\vec{b}|=|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|\);
③ \(|\vec{a}|-|\vec{b}|=|\vec{a}+\vec{b}|<|\vec{a}|+|\vec{b}|\);④ \(|\vec{a}|-|\vec{b}|<|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}|\).
A.\(0\) \(\qquad \qquad \qquad \qquad\) B.\(1\) \(\qquad \qquad \qquad \qquad\) C.\(2\) \(\qquad \qquad \qquad \qquad\) D.\(3\)
2.向量\(\vec{a}\),\(\vec{b}\)满足\(|\vec{a}|=8\),\(|\vec{b}|=12\),则\(|\vec{a}+\vec{b}|\)的最大值是\(\underline{\quad \quad}\).
3.已知\(|\vec{a}|=2\),\(|\vec{b}|=1\),则\(|\vec{a}-\vec{b}|\)的取值范围是\(\underline{\quad \quad}\).
参考答案
-
答案 \(A\)
解析 如图:在边长为\(1\)的正方形中,设\(\vec{a}=\overrightarrow{A C}\),\(\vec{b}=\overrightarrow{A B}\),
则有\(|\vec{a}|-|\vec{b}|=0\), \(|\vec{a}+\vec{b}|=|\overrightarrow{A D}|=\sqrt{2}\),\(|\vec{a}|+|\vec{b}|=2\),故①可能正确;
当\(\vec{a}\),\(\vec{b}\)都是\(\vec{0}\)时,②正确,
如果在同一条直线上.两个向量相反③正确,
当\(\vec{a}\),\(\vec{b}\)同向且都不为\(\vec{0}\)时,④正确
综合选项,一定不能成立的个数是\(0\),
故选:\(A\).
-
答案 \(20\)
解析 由性质 \(\text { 卋 }|\vec{a}+\vec{b}| \leqslant|\vec{a}|+|\vec{b}|\),
可知当\(\vec{a}\),\(\vec{b}\)方向相同时,\(|\vec{a}+\vec{b}|\)取得最大值\(|\vec{a}|+|\vec{b}|=20\).
故答案 为:\(20\). -
答案 \([1,3]\)
解析 由\(|\vec{b}|=1\),得\(|-\vec{b}|=1\),
由 \(|| \vec{a}|-|-\vec{b}|| \leqslant|\vec{a}+(-\vec{b})| \leqslant|\vec{a}|+|-\vec{b}|\),
得 \(1 \leqslant|\vec{a}-\vec{b}| \leqslant 3\).
【题型3】 向量加法的运用
【典题1】 用向量方法证明对角线互相平分的四边形是平行四边形.
证明根据向量加法的三角形法则有\(\overrightarrow{A B}=\overrightarrow{A O}+\overrightarrow{O B}\), \(\overrightarrow{D C}=\overrightarrow{D O}+\overrightarrow{O C}\).

又\(\overrightarrow{A O}=\overrightarrow{O C}\), \(\overrightarrow{D O}=\overrightarrow{O B}\),
\(\therefore \overrightarrow{A O}+\overrightarrow{O B}=\overrightarrow{D O}+\overrightarrow{O C}\),
\(\therefore \overrightarrow{A B}=\overrightarrow{D C}\).
\(∴AB∥DC\)且\(AB=DC\),
即\(AB\)与\(DC\)平行且相等.
\(∴\)四边形\(ABCD\)是平行四边形.
【典题2】在长江某渡口上,江水以\(2 km/h\)的速度向东流,长江南岸的一艘渡船的速度为\(2 \sqrt{3} \mathrm{~km} / \mathrm{h}\),要使渡船渡江的时间最短,求渡船实际航行的速度的大小和方向.
解析 要使渡江的时间最短,渡船应向垂直于对岸的方向行驶,
设渡船速度为\(\overrightarrow{v_1}\),水流速度为\(\overrightarrow{v_2}\),船实际航行的速度为\(\overrightarrow{v}\),则 \(\vec{v}=\overrightarrow{v_1}+\overrightarrow{v_2}\).
依题意作出平行四边形,如图.

在\(Rt△ABC\)中 ,\(|\overrightarrow{B C}|=\left|\overrightarrow{v_1}\right|=2 \sqrt{3}\), \(|\overrightarrow{A B}|=\left|\overrightarrow{v_2}\right|=2\),
\(\therefore|\overrightarrow{A C}|=|\vec{v}|=\sqrt{|\overrightarrow{A B}|^2+|\overrightarrow{B C}|^2}=\sqrt{2^2+(2 \sqrt{3})^2}=4\),
\(\tan \theta=\dfrac{|\overrightarrow{B C}|}{|\overrightarrow{A B}|}=\dfrac{2 \sqrt{3}}{2}=\sqrt{3}\).
.
\(∴\)渡船实际航行的速度大小为\(4 km/h\),方向为东偏北\(60°\).
【巩固练习】
1.一艘船以\(4km/h\)的速度沿着与水流方向成\(120^∘\)的方向航行,已知河水流速为\(2km/h\),则经过\(\sqrt{3} h\),该船实际航程为\(\underline{\quad \quad}\) \(km\).
2.一条河两岸平行,河的宽度为\(240 \sqrt{2}\)米,一个人从岸边游向对岸,已知他在静水中游泳时,速度大小为每分钟\(12 \sqrt{3}\)米,水流速度大小为每分钟\(12\)米.
①当此人垂直游向河对岸,那么他实际前进速度的大小为每分钟 \(\underline{\quad \quad}\)米;
②当此人游泳距离最短时,他游到河对岸需要\(\underline{\quad \quad}\)分钟.
参考答案
-
答案 \(6\)
解析 根据题意,画出示意图,如图所示,\(\overrightarrow{O A}\)表示水流速度,\(\overrightarrow{O B}\)表示船在静水中的速度,
则\(\overrightarrow{O C}\)表示船的实际速度,
又\(|\overrightarrow{O A}|=2\), \(|\overrightarrow{O B}|=4\), \(\angle A O B=120^{\circ}\),
则\(∠CBO=60^∘\),
所以 \(|\overrightarrow{O C}|=2 \sqrt{3}\),\(∠AOC=∠BCO=90^∘\).
所以实际速度为\(2 \sqrt{3} \mathrm{~km} / \mathrm{h}\),则实际航程为 \(2 \sqrt{3} \times \sqrt{3}=6 \mathrm{~km}\).
故答案 为:\(6\).
-
答案 ①\(24\),②\(20\).
解析 ①由题意作图如下,
由图可知,他实际前进速度的大小为每分钟 \(\sqrt{(12 \sqrt{3})^2+12^2}=24 m\),
②由题意作图如下,

此时实际前进速度的大小为 \(\sqrt{(12 \sqrt{3})^2-12^2}=12 \sqrt{2} \mathrm{~m}\),
故他游到河对岸需要\(\dfrac{240 \sqrt{2}}{12 \sqrt{2}}=20\)分钟,
故答案 为:①\(24\),②\(20\).
分层练习
【A组---基础题】
- \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D E}+\overrightarrow{E F}+\overrightarrow{F A}=\) ( )

A.\(0\) \(\qquad \qquad \qquad \qquad\) B. \(\overrightarrow{0}\) \(\qquad \qquad \qquad \qquad\) C. \(2 \overrightarrow{A D}\) \(\qquad \qquad \qquad \qquad\) D. \(-2 \overrightarrow{A D}\)
2.如图,正六边形\(ABCDEF\)中, \(\overrightarrow{B A}+\overrightarrow{C D}+\overrightarrow{F E}=\)( )

A.\(\overrightarrow{0}\) \(\qquad \qquad \qquad \qquad\) B. \(\overrightarrow{B E}\) \(\qquad \qquad \qquad \qquad\) C. \(\overrightarrow{AD}\) \(\qquad \qquad \qquad \qquad\) D. \(\overrightarrow{DF}\)
3.如图所示,点\(O\)是正六边形\(ABCDEF\)的中心,则 \(\overrightarrow{O A}+\overrightarrow{O C}+\overrightarrow{O E}=\)( )

A.\(\overrightarrow{0}\) \(\qquad \qquad \qquad \qquad\) B.\(0\) \(\qquad \qquad \qquad \qquad\)C. \(\overrightarrow{A E}\) \(\qquad \qquad \qquad \qquad\) D. \(\overrightarrow{ EA}\)
4.当两人共提重为\(|G|\)的书包时,夹角为\(θ\),用力为\(|F|\),则三者的关系为( )
A. \(|F|=\dfrac{|G|}{2 \cos \theta}\) \(\qquad \qquad \qquad \qquad\)B. \(|F|=\dfrac{|G|}{2 \sin \theta}\) \(\qquad \qquad \qquad \qquad\) C. \(|F|=\dfrac{|G|}{2 \cos \dfrac{\theta}{2}}\) \(\qquad \qquad \qquad \qquad\) D. \(|F|=\dfrac{|G|}{2 \sin \dfrac{\theta}{2}}\)
5.河中水流自西向东每小时\(10km\),小船自南岸\(A\)点出发,想要沿直线驶向正北岸的\(B\)点,并使它的实际速度达到每小时\(10 \sqrt{3} \mathrm{~km}\),该小船行驶的方向和静水速度分别为( )
A.西偏北\(30^∘\),速度为\(20km/h\) B.北偏西\(30^∘\),速度为\(20km/h\)
C.西偏北\(30^∘\),速度为\(20 \sqrt{3} \mathrm{~km} / \mathrm{h}\) D.北偏西\(30^∘\),速度为\(20 \sqrt{3} \mathrm{~km} / \mathrm{h}\)
6.在平行四边形\(ABCD\)中, \(\overrightarrow{B C}+\overrightarrow{C A}+\overrightarrow{A B}=\)\(\underline{\quad \quad}\).
7.如图所示的方格纸中有定点\(O\),\(P\),\(Q\),\(E\),\(F\),\(G\),\(H\),则 \(\overrightarrow{O P}+\overrightarrow{O Q}=\)\(\underline{\quad \quad}\) .

8.一艘船在静水中的航行速度为\(5km/h\),河水的流速为\(3km/h\),则船的实际航行的速度范围为 \(\underline{\quad \quad}\) .
9.2012年全国中学生机器人大赛选选拔赛中,机器人刚开始在原点位置,为了让机器人完成某项任务,学生给机器人设置了以下指令:先逆时针旋转\(α\)角,然后向前进\(1\)米,将该指令进行一次称为一次操作,试用向量解决以下问题.
(1)当\(\alpha=\dfrac{\pi}{3}\)时,经过几次操作才能回到原点?
(2)是否存在\(α\),使机器人经过\(10\)次操作,能首次回到原点?
10.在平行四边形\(ABCD\)的对角线\(BD\)的延长线及反向延长线上,分别取点\(F\),\(E\),使\(BE=DF\)(如图),用向量的方法证明四边形\(AECF\)也是平行四边形.

11.已知桥是南北方向,受落潮影响,海水以\(12.5km/h\)的速度向东流,现有一艘工作艇,在海面上航行检查桥墩的状况,已知艇的速度是\(25km/h\),若艇要沿着与桥平行的方向由南向北航行,则艇的航向如何确定?
12.某人在静水中游泳的速度为\(4 \sqrt{3}\)千米 时,他现在水流速度为\(4\)千米 时的河中游泳.
(1)如果他垂直游向河对岸,那么他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
参考答案
-
答案 \(B\)
解析 由向量加法的运算法则可知 \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{D E}+\overrightarrow{E F}+\overrightarrow{F A}=\overrightarrow{0}\). -
答案 \(B\)
解析 如图,正六边形\(ABCDEF\)中, \(\overrightarrow{B A}+\overrightarrow{C D}+\overrightarrow{F E}=\overrightarrow{B A}+\overrightarrow{A F}+\overrightarrow{F E}=\overrightarrow{B F}+\overrightarrow{F E}=\overrightarrow{B E}\).
故选:\(B\).
-
答案 \(A\)
解析 连接\(OB\),由正六边形的性质可得:四边形\(AOCB\)是平行四边形,
\(\therefore \overrightarrow{O A}+\overrightarrow{O C}=\overrightarrow{O B}\) , \(\overrightarrow{O B}=-\overrightarrow{O E}\),
\(\therefore \overrightarrow{O A}+\overrightarrow{O C}+\overrightarrow{O E}=\overrightarrow{O B}+\overrightarrow{O E}=\overrightarrow{0}\) ,
故选:\(A\).
-
答案 \(C\)
解析 书包受到重力和两人的拉力,
当两人共提重为\(|G|\)的书包时,人的胳膊与垂直方向的夹角为\(\dfrac{\theta}{2}\),
根据力的合成法则,则\(|F| \cdot \cos \dfrac{\theta}{2}=\dfrac{|G|}{2}\),
\(\therefore|F|=\dfrac{|G|}{2 \cos \dfrac{\theta}{2}}\),
故选:\(C\). -
答案 \(B\)
解析 如图,设水流速度为\(\overrightarrow{A C}\),静水速度为\(\overrightarrow{A D}\),实际速度为\(\overrightarrow{A B}\),
则四边形\(ABCD\)是平行四边形,\(∠BAC=90^∘\),
\(A B=10 \sqrt{3}\),\(AC=BD=10\),
\(\therefore \tan \angle B A D=\dfrac{B D}{A B}=\dfrac{\sqrt{3}}{3}\), \(\therefore \angle B A D=30^{\circ}\),\(A D=\sqrt{A B^2+B D^2}=20\).
\(∴\)小船行驶方向为北偏西\(30^∘\),速度为\(20km/h\).
故选:\(B\).
-
答案 \(\overrightarrow{0}\)
解析 \(\overrightarrow{B C}+\overrightarrow{C A}+\overrightarrow{A B}=\overrightarrow{B C}+\overrightarrow{C B}=\overrightarrow{0}\),故答案 为: \(\overrightarrow{0}\). -
答案 \(\overrightarrow{F O}\)
解析 设\(\vec{a}=\overrightarrow{O P}+\overrightarrow{O Q}\),以\(OP\)、\(OQ\)为邻边作平行四边形,
则夹在\(OP\)、\(OQ\)之间的对角线对应的向量即为向量\(\vec{a}=\overrightarrow{O P}+\overrightarrow{O Q}\),
由\(\vec{a}\)和\(\overrightarrow{F O}\)长度相等,方向相同,
\(\therefore \vec{a}=\overrightarrow{F O}\). -
答案 \([2,8](\mathrm{km} / \mathrm{h})\)
解析 一艘船在静水中的航行速度为\(5km/h\),河水的流速为\(3km/h\),
则船的实际航行的速度可能为\([2,8](\mathrm{km} / \mathrm{h})\). -
答案 (1) \(6\);(2) \(\dfrac{\pi}{5}\).
解析 (1)如图所示,
当\(\alpha=\dfrac{\pi}{3}\)时,经过\(1\)次操作到\(A_1\)点,经过\(2\)次操作到\(A_2\)点,
\(6α=2π\)(多边形外角和定理).
\(\therefore \overrightarrow{O A_1}+\overrightarrow{A_1 A_2}+\cdots+\overrightarrow{A_5 A_6}=\overrightarrow{0}\),
因此当\(\alpha=\dfrac{\pi}{3}\)时,经过\(6\)次操作才能回到原点.
(2)根据多边形外角和定理\(\alpha=\dfrac{2 \pi}{10}=\dfrac{\pi}{5}\).
\(∴\)存在 \(\alpha=\dfrac{\pi}{5}\),使机器人经过\(10\)次操作,能首次回到原点.
-
证明 \(\overrightarrow{A E}=\overrightarrow{A B}+\overrightarrow{B E}\), \(\overrightarrow{F C}=\overrightarrow{F D}+\overrightarrow{D C}\),
又 \(\overrightarrow{A B}=\overrightarrow{D C}\), \(\overrightarrow{B E}=\overrightarrow{F D}\),
\(\therefore \overrightarrow{A E}=\overrightarrow{F C}\) ,即\(AE\),\(FC\)平行且相等.
故四边形\(AECF\)是平行四边形. -
答案 北偏西\(30^∘\)
解析 如图,设渡艇速度为 \(\overrightarrow{O B}\),水流速度为 \(\overrightarrow{OA}\),
则艇实际垂直过江的速度为 \(\overrightarrow{O D}\),
由题意知, \(|\overrightarrow{O A}|=12.5\), \(|\overrightarrow{O B}|=25\),
\(∵\)四边形\(OADB\)为平行四边形,
\(\therefore|\overrightarrow{B D}|=|\overrightarrow{O A}|\),
又\(∵OD⊥BD\),
\(∴\)在\(Rt△OBD\)中,\(∠BOD=30^∘\),
则航向为北偏西\(30^∘\).
-
答案 (1) 与河岸成\(60^∘\)角的方向前进,实际前进速度的大小为\(18km/h\);
(2) 与水流方向成\(90^∘+θ\)(锐角\(θ\)满足\(\tan \theta=\dfrac{\sqrt{2}}{2}\),或 \(\sin \theta=\dfrac{\sqrt{3}}{3}\)等)方向航行,实际前进速度的大小为\(4 \sqrt{2}(\mathrm{~km} / \mathrm{h})\).
解析 (1)如图①,由于\(V_{\text {实 }}=V_{\text {水 }}+V_{\text {人 }}\),
\(\therefore\left|V_{\text {买 }}\right|=\sqrt{(4 \sqrt{3})^2+4^2}=8(\mathrm{~km} / \mathrm{h})\),
又 \(\tan \theta=\dfrac{\left|v_{\text {人 }}\right|}{\left|v_{\text {水 }}\right|}=\dfrac{4 \sqrt{3}}{4}=\sqrt{3}\),
\(∴θ=60^∘\),
\(∴\)他必须沿与河岸成\(60^∘\)角的方向前进,实际前进速度的大小为\(18km/h\).
(2)如图②,解直角三角形可得 \(\left|v_{\text {实 }}\right|=\sqrt{(4 \sqrt{3})^2-4^2}=4 \sqrt{2}(\mathrm{~km} / \mathrm{h})\),
又 \(\tan \theta=\dfrac{\left|v_{\text {人 }}\right|}{\left|v_{\text {实 }}\right|}=\dfrac{4}{4 \sqrt{2}}=\dfrac{\sqrt{2}}{2}\),
\(∴\)他必须沿与水流方向成\(90^∘+θ\)(锐角\(θ\)满足\(\tan \theta=\dfrac{\sqrt{2}}{2}\),或 \(\sin \theta=\dfrac{\sqrt{3}}{3}\)等)方向航行,实际前进速度的大小为\(4 \sqrt{2}(\mathrm{~km} / \mathrm{h})\).
【B组---提高题】
1.点\(O\)是\(△ABC\)所在平面上一点,且满足\(\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{0}\),则点\(O\)为\(△ABC\)的( )
A.外心 \(\qquad \qquad \qquad \qquad\) B.内心 \(\qquad \qquad \qquad \qquad\) C.重心 \(\qquad \qquad \qquad \qquad\) D.垂心
2.已知向量\(\vec{a}\),\(\vec{b}\)满足 \(|\vec{a}-\vec{b}|=|\vec{a}+3 \vec{b}|=2\),则\(|\vec{a}|\)的取值范围是\(\underline{\quad \quad}\).
3.平面上三个力\(F_1,F_2,F_3\)作用一点\(O\), \(\left|F_1\right|=1 N\), \(\left|F_2\right|=\dfrac{\sqrt{6}+\sqrt{2}}{2} N\), \(\left|F_3\right|=(\sqrt{3}+1) N\),若使这三个力作用于点\(O\)处于平衡状态,则三个力之间的夹角分别为多少?
参考答案
-
答案 \(C\)
解析 作\(BD//OC\),\(CD//OB\),连结\(OD\),\(OD\)与\(BC\)相交于\(G\),则\(BG=CG\),
\(\therefore \overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O D}\),
又 \(\because \overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{0}\),可得: \(\overrightarrow{O B}+\overrightarrow{O C}=-\overrightarrow{O A}\),
\(\therefore \overrightarrow{O D}=-\overrightarrow{O A}\) ,
\(∴A,O,G\)在一条直线上,可得\(AG\)是\(BC\)边上的中线,
同理:\(BO\),\(CO\)的延长线也为\(△ABC\)的中线.
\(∴O\)为三角形\(ABC\)的重心.
故选:\(C\).
-
答案 \([1,2]\)
解析 \(\because|\vec{a}-\vec{b}|=|\vec{a}+3 \vec{b}|=2\), \(\therefore|3 \vec{a}-3 \vec{b}|=6\),
\(\therefore 2+6=|\vec{a}+3 \vec{b}|+|3 \vec{a}-3 \vec{b}| \geqslant|\vec{a}+3 \vec{b}+3 \vec{a}-3 \vec{b}| \geqslant|4 \vec{a}|\), \(\therefore|\vec{a}| \leqslant 2\),
\(\because|3 \vec{b}-3 \vec{a}|-|\vec{a}+3 \vec{b}| \leqslant|3 \vec{b}-3 \vec{a}-\vec{a}-3 \vec{b}|=|3 \vec{b}-\overrightarrow{3 a}| \leqslant|4 \vec{a}|\),
\(\therefore|\vec{a}| \geqslant 1\),
\(\therefore|\vec{a}|\)的取值范围是 \([1,2]\),
故答案 为: \([1,2]\). -
答案 \(\vec{F_1 }\)与\(\vec{F_2 }\)的夹角为\(45^∘\), \(\vec{F_1 }\)与\(\vec{F_3}\)的夹角为\(150^∘\).
解析 如图所示,
分别作\(\overrightarrow{O A}=\vec{F_1 }\),\(\overrightarrow{O B}=\overrightarrow{F_2}\), \(\overrightarrow{O C}=\overrightarrow{F_3}\). \(\angle A O B=\alpha\), \(\angle A O C=\beta\).
假设这三个力作用于点\(O\)处于平衡状态,
\(\therefore \dfrac{\sqrt{6}+\sqrt{2}}{2} \cos \alpha+(\sqrt{3}+1) \cos \beta+1=0\), \(\dfrac{\sqrt{6}+\sqrt{2}}{2} \sin \alpha-(\sqrt{3}+1) \sin \beta=0\),
化为 \(\left(\dfrac{\sqrt{6}+\sqrt{2}}{2}\right)^2+(\sqrt{3}+1)^2+\sqrt{2}(\sqrt{3}+1)^2 \cos (\alpha-\beta)=1 \cdot \dfrac{\sin \alpha}{\sin \beta}=\sqrt{2}\).
\(\therefore \cos (\alpha+\beta)=\dfrac{-5-3 \sqrt{3}}{2 \sqrt{2}(2+\sqrt{3})}=-\dfrac{\sqrt{6}+\sqrt{2}}{4}=\cos 195^{\circ}\),
\(∴α+β=195^∘\),
\(\therefore \sin \left(195^{\circ}-\beta\right)=\sqrt{2} \sin \beta\),化为\(\tan \beta=-\dfrac{\sqrt{3}}{3}\),解得 \(β=150^∘\),\(α=45^∘\).
\(∴\vec{F_1 }\)与\(\vec{F_2 }\)的夹角为\(45^∘\), \(\vec{F_1 }\)与\(\vec{F_3}\)的夹角为\(150^∘\).