标签：gcd 数论 dfrac 知识 pmod cdots 事件一些 2n

欧拉函数

定义

$1-N$中与 $N$ 互质的个数被称为欧拉函数，记为 $φ(n)$。

公式

设 $n={p_1}^{c_1}*{p_2}\cdots^{c_m}$
则 $φ(n)=n\dfrac{p_1-1}{p_1}\dfrac{p_2-1}{p_2}\cdots\dfrac{p_m-1}{p_m}$

性质

$φ(1)=1$，
因为 $1$ 的质因数个数为 $0$，
所以原式$=1$
$n$ 为质数，则 $φ(n)=n-1$，
因为原式$=n*\dfrac{n-1}{n}=n-1$
$n$ 为质数，则 $φ(n^k)=(n-1)*n$，
因为原式$=n^{k*\dfrac{n-1}{n}=n}*(n-1)$
当 $n,m$ 互质，$φ(nm)=φ(n)φ(m)$，
因为如果设
$n={p_1}^{c_1}*{p_2}\cdots^{c_x}$，
$m={q_1}^{d_1}*{q_2}\cdots^{d_y}$，
则 $φ(nm)=nm\dfrac{p_1-1}{p_1}\dfrac{p_2-1}{p_2}\cdots\dfrac{p_x-1}{p_x}\dfrac{q_1-1}{q_1}\dfrac{q_2-1}{q_2}\cdots\dfrac{q_y-1}{q_y}$
$=n\dfrac{p_1-1}{p_1}\dfrac{p_2-1}{p_2}\cdots\dfrac{p_x-1}{p_x}m\dfrac{q_1-1}{q_1}\dfrac{q_2-1}{q_2}\cdots\dfrac{q_y-1}{q_y}$
$=φ(n)φ(m)$
$n$ 为质数，$\begin{cases}p%n=0,φ(pn)=φ(p)n\p%n\neq0,φ(pn)=φ(p)(n-1)\end{cases}$
因为，第二条由④与②得。而当 $n%p=0$ 时，每增加 $n$ 就会少一个互质数，所以最终少 $φ(n)$ 个。
当 $n>1$ 时，$s=1-n$ 与 $n$ 互质的整数和 $=nφ(n)/2$
令 $x<n,gcd(x,n)=1$ 则 $gcd(n,n-x)$ ，所以 $x∈{1,a2,\cdots ,aφ(n)/2,- n-aφ(n)/2,\cdots,n-a2,n-1}$ ，等差数列得 $nφ(n)/2$
$\sum_{d|n} φ(d)=n$

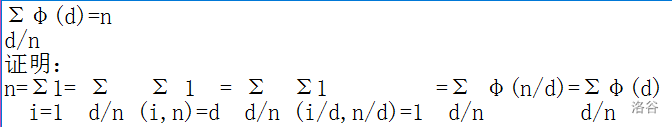
同余

定义

当 $a%m=b%m$ 时，我们称 $a,b$ 关于 $mod$ $m$ 同余。记作 $a\equiv b\pmod{m}$。

定理

$a\equiv b\pmod{m}$ ，当且仅当 $m|(a-b)$。
$a\equiv b\pmod{m}$ ，当且仅当存在整数 $k$，使得 $a=b+k*m$。

性质

1、自反性：$a≡a\pmod m$
2、对称性：若 $a ≡ b\pmod m$，则 $b ≡ a\pmod m$
3、传递性：若 $a ≡ b\pmod m$，$b ≡ \pmod m$，则 $a ≡ c\pmod m$
4、同加性：若 $a ≡ b\pmod m$，则 $a+c ≡ b+c\pmod m$
5、同乘性：若 $a ≡ b\pmod m$，则 $ac ≡ bc\pmod m$
6、同幂性：若 $a ≡ b\pmod m$，则 $a^n ≡ b^n\pmod m$
7、若 $a % p=x,a % q=x,\gcd(p,q)=1$，则$a %(p*q)=x$

欧拉定理

当 $gcd(a,m)=1$ ，会有 $a^{\varphi(m)}≡1\pmod m$。
证明:
既约剩余系：所有关于 $m$ 同余的数组成的集合称为模 $m$ 的一个剩余类。在模 $m$ 的每个互质剩余类中任取一数，我们称所有的数所组成的集为模 $m$ 的一个既约剩余系，项数为 $\varphi(m)$。

设 $S={b_1,b_2,\cdots b_{\varphi (m)}}$ 为模 $m$ 的一个既约剩余系。
因为 $gcd(a,m)=1,gcd(b_i,m)=1(1 \le i \le \varphi (m))$
所以 $S'={ab_1,ab_2,\cdots ab_{\varphi (m)}}$ 也为模 $m$ 的一个既约剩余系，$S=S'$。
所以 $S≡S'\pmod m$
$\prod_{i=1}^{φ(m)}b_i ≡ \prod_{i=1}^{φ(m)}(ab_i)\pmod m$
$ \prod_{i=1}^{φ(m)}(a*b_i) ≡ \prod_{i=1}^{φ(m)}b_i\pmod m$
$m|\prod_{i=1}^{{φ(m)}(a*b_i)-\prod_{i=1}}b_i\pmod m$
$m|(a^{{φ(m)}-1)\prod_{i=1}}b_i\pmod m$
因为 $S$ 为模 $m$ 的一个既约剩余系
所以 $m|\prod_{i=1}^{φ(m)}b_i\pmod m$
所以 $m|(a^{φ(m)}-1)\pmod m$
$a^{φ(m)}-1≡0\pmod m$
$a^{φ(m)}≡1\pmod m$

费马小定理

当 $p$ 为质数，$a^p≡a\pmod p$。
证明:
当 $\gcd(p,a)=1$ ，根据欧拉定理，$a^{φ(p)}≡1\pmod p$
因为 $φ(p)=p-1$
所以 $a^{p-1}≡1\pmod p$
$a^p≡a\pmod p$
当 $\gcd(p,a)\neq 1$，即 $a$ 为 $p$ 的倍数。
所以 $a^p|p,a|p$
所以 $a^p≡a\pmod p$

扩展欧几里得

贝祖定理

对于任意整数 $a,b$ 存在整数 $x,y$，满足 $ax+by=\gcd(a,b)$
在辗转相除中求解：$ax+by=\gcd(a,b)=\gcd(b,a%b)=bx'+(a%b)y'$
$=bx'+(a-\lfloor\dfrac{a}{b}\rfloorb)y'$
$=bx'+ay'-\lfloor\dfrac{a}{b}\rfloorby'$
$=ay'+b(x'-\lfloor\dfrac{a}{b}\rfloory')$
所以 $x=y'$，$y=x'-\lfloor\dfrac{a}{b}\rfloory'$。递归求解
通解：
设辗转相除中的解为 $x_0,y_0$ ，则通解满足：
$x=x_0+b/\gcd(a,b)t$
$y=y_0-a/\gcd(a,b)t$
$t$ 为任意整数
证明：
设 $x=x_0+k_1,y=y_0+k_2$
则 $ax_0+ak_1+by_0+bk_2=\gcd(a,b)$
$ak_1+bk_2=0$
有特殊解 $k_1=b,k_2=-a$
有最小解 $k_{1_0}=\dfrac{b}{\gcd(a,b)},k_{2_0}=\dfrac{a}{\gcd(a,b)}$
其他解扩倍则 $t(\dfrac{b}{\gcd(a,b)}+\dfrac{a}{\gcd(a,b)})=0$
所以 $x=x_0+b/\gcd(a,b)t$，$y=y_0-a/\gcd(a,b)t$
最小非负整数解：
$x_0$ 每次移动 $b/\gcd(a,b)$ 单位，最终 $x_0-b/\gcd(a,b)i>0$ 并且 $x_0-b/\gcd(a,b)(i+1)<0$。
则 $x=(\underline{x_0%(b/\gcd(a,b)}+\underline{b/\gcd(a,b))%(b/\gcd(a,b))}$
(限定范围)(取非负)

解方程 $ax+by=n$

条件：$\gcd(a,b)|n$
过程：

扩欧求得 $ax+by=gcd(a,b)$ 的解 $x_0,y_0$
求得原方程特解 $x_1=x_0n/\gcd(a,b),y_1=y_0n/\gcd(a,b)$
套用通解 $x=x_1+b/\gcd(a,b)t$ $y=y_1-a/\gcd(a,b)t$

线性同余方程

基本形式：$ax≡\pmod m$
条件：$\gcd(a,m)|b$
转化：$ax≡b\pmod m ->m|(ax-b)->ax-my=b->ax+m*y=b$

逆元

定义：当 $\gcd(m,b)=1$ 且 $b|a$，则有整数 $x$ ，满足 $\dfrac{a}{b}≡ax\pmod m$ ，称 $x$ 为 $b$ 的模 $m$ 乘法逆元，记为 $b^{-1}\pmod m$。
扩欧求逆元：
当 $\gcd(a,m)=1$ 时，
$\dfrac{a}{b}≡\dfrac{a}{b}bb^{-1}\pmod m$
$1≡bx\pmod m$
解方程
费马小求逆元：
当 $m$ 为质数，$b<m$ 时，由费马小定理得 $b^m≡b\pmod m$
$b^{m-1}≡1\pmod m$
$bb^{m-2}≡1\pmod m$
$x=b^{m-2}$
递推求逆元：
当 $i<p$，$p$ 为质数时，$p=ki+r$，其中 $k=p/i,r=p%i$
$(ki+r)≡0\pmod p$
$(kii^{-1}+r*i) ≡0\pmod p$
$ri^{-1} ≡-k\pmod p$
$i^{-1} ≡-kr^{-1}\pmod p$
$i^{-1} ≡-(p/i)(p%i)^{-1}\pmod p$
$i^{-1} ≡(p-p/i)(p%i)^{-1}\pmod p$
则 $ny_i=(p-p/i)ny_{p%i}%p$

中国剩余定理

CRT

定义：
$\begin{cases}x≡a_1\pmod {m_1}\x≡a_2\pmod {m_2}\\cdots\x≡a_n\pmod {m_n}\end{cases}$
当 $m_1,m_2,\cdots,m_n$ 两两互质，$\dfrac{\prod_{i=1}^{n}m_i}{m_i}t_i≡a_i\pmod {m_i}$，解为 $x=\sum_{i=1}^n (a_it_i\dfrac{\prod_{i=1}^{n}m_i}{m_i})$
证明：
当 $m_1,m_2,\cdots,m_n$ 两两互质：
设 $m_{i_{lcm}}=lcm(m_1,m_2,\cdots,m_n)/m_i=\dfrac{\prod_{i=1}^{n}m_i}{m_i}$
则 $m_{i_{lcm}}t_i≡a_i\pmod {m_i}$
$m_{i_{lcm}}(t_i/a_i)≡1\pmod {m_i}$
解出 $(t_i/a_i)$
则该方程最终的解为 $m_{i_{lcm}}(t_i/a_i)a_i$
则最终解为 $x=\sum_{i=1}^n (a_it_i*m_{i_{lcm}})$

EXCRT

定义：
$\begin{cases}x≡a_1\pmod {m_1}\x≡a_2\pmod {m_2}\\cdots\x≡a_n\pmod {m_n}\end{cases}$
求解的过程
过程：
从第一个方程开始，逐个满足
设 $m=lcm(m_1,m_2,\cdots,m_i)$ ，初始 $x_1=a_1$ 。
则 $x+tm$ 是前 $i-1$ 个方程的解。
当前方程满足 $x_{i-1}+t'm≡a_i\pmod {m_i}$
即 $t'm≡a_i-1\pmod {m_i}$
求解或无解，若有解，则 $x_i=x_{i-1}+t'm$
最终输出 $x_n$

Catalan 数

定义：将 $n$ 个 $0$ 和 $n$ 个 $1$ 按照某种顺序排成长度为2n的序列，满足任意前缀 $0$ 的个数都不少于 $1$ 的个数的序列的数量。
组合公式：$Cat_n=\dfrac{1}{n+1}C^{n}{2n}$
证明：
$n$ 个 $0$ 和 $n$ 个 $1$ 组成的排列个数为 $C^{n}$。
对于一个由 $n$ 个 $0$ 和 $n$ 个 $1$ 组成的序列，必然有一个前缀有 $p$ 个 $0$ ，$p+1$ 个 $1$。对于一个由 $n'-1$ 个 $0$ 和 $n'+1$ 个 $1$ 组成的序列，也必然存在一个前缀有 $p'$ 个 $0$ ，$p'+1$ 个 $1$。所以由 $n$ 个 $0$ 和 $n$ 个 $1$ 组成的序列和由 $n'-1$ 个 $0$ 和 $n'+1$ 个 $1$ 组成的序列一一对应。由 $n'-1$ 个 $0$ 和 $n'+1$ 个 $1$ 组成的序列有 $\dfrac{(2n)!}{(n-1)!(n+1)!}=C^{{n-1}_{2n}$，则：$Cat_n=C}{2n}-C^{{n-1}_{2n}=\dfrac{(2n)!}{n!*n!}-\dfrac{(2n)!}{(n-1)!*(n+1)!}=\dfrac{1}{n+1}*C}$
递推公式：$Cat_n=\dfrac{4n-2}{n+1}Cat_{n-1}$
证明：
$Cat_n-Cat_{n-1}=(\dfrac{1}{n+1}C^{{n}_{2n})/(\dfrac{1}{n}*C}{2n-2})$
$=\dfrac{1}{n+1}*C^{{n}_{2n}*\dfrac{1}{n}/C}$
$=\dfrac{1}{n+1}\dfrac{(2n)!}{n!n!}\dfrac{1}{n}/\dfrac{(2n-2)!}{(n-1)!(n-1)!}$
$=\dfrac{4n-2}{n+1}$
所以 $Cat_n=\dfrac{4n-2}{n+1}*Cat_{n-1}$

概率与数学期望

随机试验

条件：

试验可以在相同条件下重复进行
试验可能出现的结果有多个，试验之前知道所有可能的结果
试验结束后会出现哪一个结果是随机的

定义：

基本事件($ω$)：一次试验可能出现的每一个直接的结果，也就是随机试验不能够再分解的结果。
样本空间($Ω$)：全体基本事件的集合。
标记：每个事件使用大写字母标记。
事件发生：事件 $A$ 中包含的任意基本时间发生，我们称事件 $A$ 发生。
必然事件：必然发生的事件($Ω$)。
不可能事件：必然不发生的事件($Φ$)。

运算：

$A⊂B$ 或 $B⊃A$ : 事件 $A$ 发生必然导致事件 $B$ 发生。
$A\cup B$ 或 $A+B$：事件 $A$ 与事件 $B$ 至少有一个发生。
$A\cap B$ 或 $A*B$：事件 $A$ 与事件 $B$ 同时发生。
$A-B$：事件 $A$ 发生而事件 $B$ 不发生。
$B=A$ 或 $A=B$：事件 $A$ 与事件 $B$ 不能同时发生。($A\cap B=Φ,A\cup B=Ω$)
$A|B$：$A$ 和 $B$ 为两事件，且 $P(A)>0$，则称 $P(AB)/P(A)$ 为事件 $A$ 发生的条件下事件 $B$ 发生的条件概率，记作 $P(B|A)$，即 $P(B|A)= P(AB)/P(A)$

离散概率模型

定义：

试验中所有可能出现的基本事件只有有限个。
试验中每个基本事件出现的可能性相等。

公式：
设 $A$ 由 $m$ 个基本事件组成，共 $n$ 个基本事件
则发生 $A$ 的概率 $P(A)=\dfrac{m}{n}$

连续概率模型

定义：

试验中所有可能出现的基本事件有无限个。
试验中每个基本事件出现的可能性相等。

公式：
设 $A$ 长 $m$ ，共长 $n$ 。
则发生 $A$ 的概率 $P(A)=\dfrac{m}{n}$

公式

划分：
$A_1,A_2,\cdots,A_n$ 为样本空间 $S$ 的划分当：

$U_{i=1}^na_i=S$
$A_i*A_j=Φ(1 \le i,j \le n,i\neq j)$

全概率公式：
设 $A_1,A_2\cdots,A_n$ 为 $S$ 的一个划分且 $P(A_i)>0$，则：
$P(A)$
$=\sum_{i=1}^nP(AB_i)$
$=\sum_{i=1}^nP(B_i)P(A|B_i)$
贝叶斯公式:
$P(A_j|B)=\dfrac{P(A_jB)}{P(B)}=\dfrac{P(A_j)P(B)}{\sum_{i=1}^nP(A_i)*P(B|A_i)}(1 \le i \le n)$

数学期望

定义：设 $X$ 为离散的随机边量，它的值为 $X_i(1 \le i \le n)$ 的概率为 $P_i$ 。则数学期望 $E[X]=\sum_{i=1}^n(X_i*P_i)$
性质：

$E[X+c]=E[X]+c$
$E[Xc]=E[X]c$
$E[X+Y]=E[X]+E[Y]$
$E[aX+bY]=aE[X]+bE[Y]$

方差

定义：“期望值离散程度”的期望值
公式：设 $X$ 为离散的随机边量，它的值为 $X_i(1 \le i \le n)$ 的概率为 $P_i$ 。则方差 $V[X]=E[(X-\mu)^{2]=\sum_{i=0}}nP(x_i)*(x_i-\mu)^2$。其中 $\mu=E[X]$
性质：

$V[X+c]=V[X]$
$V[Xc]=c^2V[x]$
$V[X]=E[X^2]-E[X]2$

标签：gcd,数论,dfrac,知识,pmod,cdots,事件,一些,2n
From： https://www.cnblogs.com/lizhous/p/17369084.html

一些数论知识