割点与割边

定义

连通分量：在一张无向图中的极大连通子图即为该图的连通分量。

割点：去掉这个点后，这张无向图的连通分量数量增加，则这个点称为这个图的割点。

割边：去掉这条边后，这张无向图的连通分量数量增加，则这条边称为这个图的割边。

求割点

主要思路

以下提到的有关树的内容，全部指的是对连通分量做 DFS 得到的 DFS 生成树上的内容。

我们对一个连通分量做一次 DFS，可以得到一棵搜索树。这里引入两个定理：

1. 如果这棵 DFS 生成树的根节点至少有两个儿子节点，那么这个根节点是割点。

2. 这棵 DFS 生成树中的非根节点的一个儿子节点不能不通过它们之间的连边回到这个点的祖先，那么这个点就是割点。

先看定理 \(1\)：

这个很好理解，如果这个根节点不是割点，说明根节点只有一个儿子，因为其他点都可以在不经过根节点的情况下两两到达。看图：

图中黑色边为以 \(1\) 为根的搜索树边，红色边为原图中的边。由于 \(1\) 只有一个儿子，所以 \(1\) 不为割点。

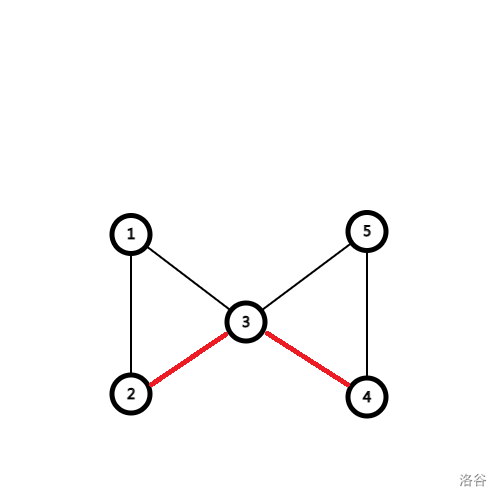
否则将这个节点删掉，一定会使连通分量的数量增加，因为有节点必须通过根节点才能到达别的节点。如图：

、

黑色边是以 \(3\) 为根的搜索树边，红色边为原图中的边。可以看到，根节点 \(3\) 拥有两个儿子，因为 \(1\) 与 \(4\)，\(2\) 与 \(5\) 等都不能在不经过 \(3\) 的情况下互达，所以 \(3\) 为割点。

我们再看定理 \(2\)：

如果删掉这个点，连通分量数量变多，说明有点不再与其他点连通，即没有返祖边连回这个点的祖先。否则一定可以通过这条返祖边连回这个点的祖先，那么连通分量数量也不会增加。

在这个图中，搜索树以 \(1\) 为根，可以发现，节点 \(4\) 无法不通过 \(4 - 5\) 这条边返回 \(5\) 的祖先，所以 \(5\) 是割点。如果加上 \(1 - 4\) 的一条边，再将 \(5\) 节点删去：

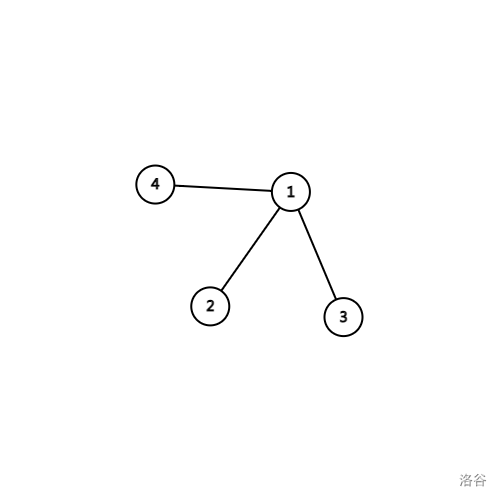
可以看到，连通分量数量并没有增加。因为节点 \(4\) 可以通过 \(1-4\) 的返祖边退回 \(5\) 的祖先 \(1\)，所以并不会断开。

那么要如何实现呢？我们可以在 dfs 时记录一个点的 \(dfn\)（dfs 序），以及这个点的儿子节点中能回到的祖先的最小的 \(dfn\)，记为 \(low\)。

那么如何更新 \(low\)？假如现在遍历到节点 \(u\)，下一步要遍历节点 \(v\)：

1. 在遍历完 \(v\) 后回溯时，用 \(low_v\) 更新 \(low_u\)。

2. 如果 \(u - v\) 是返祖边，用 \(dfn_v\) 更新 \(low_u\)。

那么判断割点也很好判断了，根据定理 \(2\)，如果这时 \(low_v \ge dfn_u\)，那么 \(u\) 是割点，因为 \(v\) 不能通返祖边回到 \(u\) 的祖先节点。对于定理 \(1\) 记录儿子个数特判即可。

举个例子：

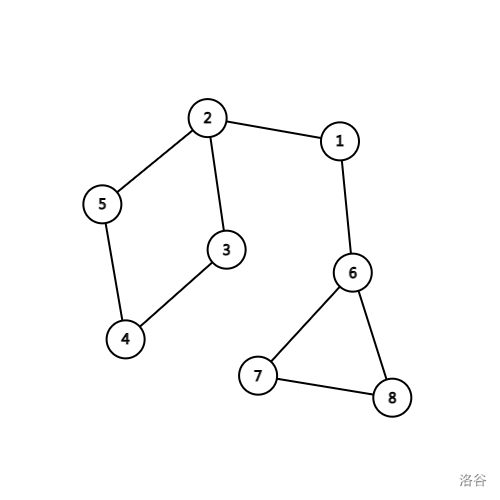
对于上图，我们从 \(1\) 开始 dfs，整个算法过程如下：

遍历节点 \(1\)，\(dfn_1\) 赋值为 \(1\)，\(low_1\) 赋值为 \(1\)；

遍历节点 \(2\)，\(dfn_2\) 赋值为 \(2\)，\(low_2\) 赋值为 \(2\)，根节点 \(1\) 的儿子数更新为 \(1\)；

遍历节点 \(5\)，\(dfn_5\) 赋值为 \(3\)，\(low_5\) 赋值为 \(3\)；

遍历节点 \(4\)，\(dfn_4\) 赋值为 \(4\)，\(low_4\) 赋值为 \(4\)；

遍历节点 \(3\)，\(dfn_3\) 赋值为 \(5\)，\(low_3\) 赋值为 \(5\)；

发现节点 \(2\) 已经被遍历，所以 \(3 - 2\) 是一条返祖边，将 \(low_3\) 更新为 \(2\)；

回溯至节点 \(4\)，将 \(low_4\) 更新为 \(2\)；

回溯至节点 \(5\)，将 \(low_5\) 更新为 \(2\)；

回溯至节点 \(2\)；

回溯至节点 \(1\)，由于 \(low_2 \ge dfn_1\)，所以 \(2\) 是割点；

遍历节点 \(6\)，\(dfn_6\) 赋值为 \(6\)，\(low_6\) 赋值为 \(6\)，根节点 \(1\) 的儿子数更新为 \(2\)；

遍历节点 \(7\)，\(dfn_7\) 赋值为 \(7\)，\(low_7\) 赋值为 \(7\)；

遍历节点 \(8\)，\(dfn_8\) 赋值为 \(8\)，\(low_8\) 赋值为 \(8\)；

发现节点 \(6\) 已经被遍历，所以 \(8-6\) 是一条返祖边，将 \(low_8\) 更新为 \(6\)；

回溯至节点 \(7\)，将 \(low_7\) 更新为 \(6\)；

回溯至节点 \(6\)；

回溯至节点 \(1\)，由于 \(low_6 \ge dfn_1\)，所以 \(6\) 是割点；

由于根节点 \(1\) 的儿子数 \(\ge 2\)，所以根节点 \(1\) 是割点。

所以这张图上的割点为 \(1,2,6\)。

code

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,dfn[maxn],low[maxn],f[maxn],cnt;
vector<int> G[maxn];
void dfs(int cur,int u,int fa){
	dfn[u]=low[u]=++cnt;
	int sum=0;
	for(int i=0;i<G[u].size();i++){
		int v=G[u][i];
		if(!dfn[v]){
			sum++;
			dfs(cur,v,u);
			low[u]=min(low[u],low[v]);
			if(low[v]>=dfn[u]&&u!=cur){
				f[u]=1;
			}
		}
		else if(dfn[v]<dfn[u]&&v!=fa){
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(u==cur&&sum>=2){
		f[cur]=1;
	}
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v;
		cin>>u>>v;
		G[u].push_back(v);
		G[v].push_back(u); 
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]){
			dfs(i,i,-1);
		}
	} 
	int ans=0;
	for(int i=1;i<=n;i++){
		if(f[i]) ans++;
	}
	cout<<ans<<endl;
	for(int i=1;i<=n;i++){
		if(f[i]) cout<<i<<" "; 
	} 
	return 0;
}

求割边

求割边，只要将求割点的条件从 \(low_v \ge dfn_u\) 改为 \(low_v > dfn_u\) 就可以了。

为什么？

考虑何时 \(low_v = dfn_u\)。

当从 \(v\) 出发不经过 \(u-v\) 能到达 \(dfn\) 最小的点为 \(u\) 时，\(low_v = dfn_u\)。也就意味着 \(v\) 不通过 \(u-v\) 最多只能返回父亲 \(u\)。如图：

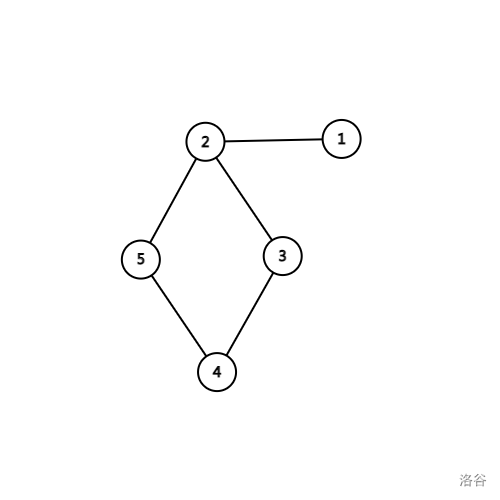
图中节点 \(2\) 是一个割点。它的 \(dfn\) 为 \(2\)，而它在 dfs 树上的儿子 \(5\) 的 \(low=2\)，节点 \(5\) 不经过 \(5-2\) 最多只能返回 \(2\)，所以 \(2\) 是割点。

但是我们注意到 \(1-2\) 这一条边：它是一条割边。图中 \(dfn_1=1\)，而 \(low_2=2\)，说明 \(2\) 不经过 \(1-2\) 最多只能到 \(2\)，连父亲节点也回不去了，所以 \(1-2\) 自然就是割边。

双连通分量

定义

点双连通分量：如果一个连通分量中不存在割点，则这个连通分量称为点双连通分量。

边双连通分量：如果一个连通分量中不存在割边，则这个连通分量称为边双连通分量。

求点双连通分量

问题：在一张无向图 \(G\) 上，有多少个点双？

这里有一个性质：割点会把一个连通分量分为若干个点双。

所以我们在求解割点的时候，使用栈来记录已经遍历过的边。当我们找到割点的时候，我们已经完成了对一个点双的遍历，所以此时栈中的元素就是一个点双。

为什么放入栈中的不是点，是边？

因为一条边只属于一个点双，而一个点可以属于多个点双，当这个点被弹出，就意味着这个点不能属于其他点双，所以存点会错。