埃氏筛法
说到筛质数,就不得不提到大名鼎鼎的埃氏筛法了
思想非常简单,就是对于每一个素数pri[i],我们都把它的倍数筛去,
譬如对于素数2来说,我们就把\(2*2, 2*3, 2*4, 2*5 .... 2*n\) 的数全部筛掉
代码
void zhishu(int n){
for(int i=2;i<=n;i++){
if(p[i]==0)
for(int j=i*2;j<=n;j+=i)
p[j]=1;
}
}
实际上我们可以发现,对于30来说,它被2筛过,被3筛过,被5筛过,
显然这种算法并不是最优的,因为对于同样的一个数,它被筛了多次
它的时间复杂度是\(O(n\ log\ log n)\)
线性筛
分析
对于每一个数,我们都希望它只被它最小的质因子筛掉,
譬如说我们希望18被2筛掉,而不是被3筛掉,
而30被2筛掉,不是被3,5筛掉
举个例子,当\(pri[]={2,3,5},i=6\)时,我们先把$12=2*6 $筛去,
但是我们发现,对于$18=3 * 6 $来说,我们没有必要把18筛掉,
因为$ 18=3* 6=3(3 2)=2 * 9 $,也就是说当i=9的时候,我们会把\(18=2* 9\)筛掉,所以现在就没有必要筛掉18
对于 i%prime[j] ==0 就break的解释 :
当 i是prime[j]的倍数时,i = k * prime[j],
如果继续运算 j+1,i * prime[j+1] = prime[j] * k * prime[j+1],
这里i * prime[j+1] 应该被 prime[j] 筛掉而不是prime[j+1]
所以才跳出循环。
因此,对于任意一个数,它都会只访问一次,所以时间复杂度就达到了\(O(n)\)的级别
欧拉筛还有一个优点,就是它在筛质数的过程中会把质数都存储下来,就比埃氏筛法更加的方便
线性筛的本质就是对于一个i,我们先把质数表中和i互质的数筛掉,然后再筛一个最大公约数为当前质数的数就退出循环
代码
void ols(){
for(int i=2;i<=n;i++){
if(!d[i])pri[++len]=i;
for(int j=1;pri[j]*i<=n&&j<=len;j++){
d[pri[j]*i]=true;
if(i%pri[j]==0)break;
}
}
}
欧拉函数
欧拉函数\(φ(n)\)表示小于等于n,且与n互质的正整数的个数。
如何求\(φ(n)\)?
比如\(φ(12)\)
把12质因数分解,\(12=2^2*3\),其实就是得到了2和3两个互异的质因子
然后把2的倍数和3的倍数都删掉
2的倍数:\(2,4,6,8,10,12\)
3的倍数:\(3,6,9,12\)
但是是6和12重复减了
所以还要把即是2的倍数又是3的倍数的数加回来
所以这样写\(12 - \frac{12}{2} -\frac{ 12}{3} +\frac{ 12}{2*3}\)
这是容斥原理!
特别地, \(\varphi(1) = 1\)

代码
//求n的欧拉函数值: phi[n]
int getPhi(int n){
int ans = n;
for(int i = 2; i*i <= n; i++){
if(n % i == 0){
ans = ans * (i-1)/i;
while(n % i == 0) n /= i;
}
}
if(n > 1) ans = ans * (n-1)/n ;
return ans;
}
//时间复杂度:sqrt(n)
欧拉函数的一些性质
性质
1、\(对于任意一个质数p,\varphi(n)=n-1\)
2、\(当gcd(n,m)=1时,\varphi(nm)=\varphi(n)\varphi(m)\)
3、\(若n=p^k 其中p为质数,则\varphi(n)=p^k-p^{k-1}=(p-1)p^{k-1}\)
4、$n= p_1{k_1}p_2 \dots p_{m-1}{k_{m-1}}p_m 其中 p_m^{k_m} 为n所分解的质因数(k_m为每个质因数的个数) ,则\varphi(n) = n \prod_{i=1}^m(1- \frac{1}{p_i}) $
5、\(所有小于n与n互质的数的和sum=n \times \frac{\varphi(n)}{2}=\sum\limits_{d=1}^{n}[gcd(d,n)=1]\)
6、\(如果i\mod p = 0,其中p为质数则\varphi(i*p)=p*\varphi(i)否则\varphi(i*p)=(p-1)\varphi(i)\)
7、\(n= \sum_{d|n}\varphi(d)\)
8、$欧拉定理:对于互质的整数a,m,有a^{\varphi(m)} \equiv 1 $
9、\(欧拉降幂公式 A^K\equiv A^{K \%\phi(m) +\phi(m)}(\mod \ m);\)$ K > \phi(m) $
10、\(\varphi(a*b)=\varphi(a)*\varphi(b)*\frac{d}{\varphi(d)},其中d=gcd(a,b)\)
证明

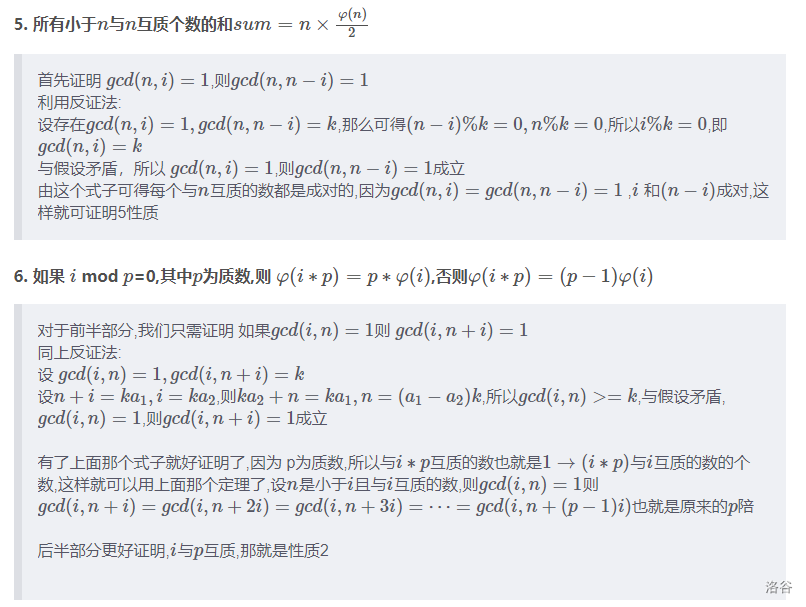

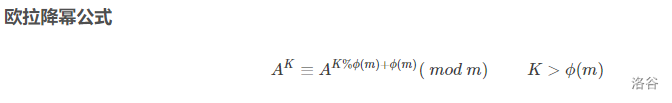

积性函数
定义
\[如果一个数论函数 f(n)满足 f(pq)=f(p)\times f(q),\gcd(p,q)=1,则称 f(n) 是一个积性函数。\\ 特别的,如果不要求 \gcd(p,q)=1 且依然满足上述式子的话,则称 f(n) 是一个完全积性函数。 \]
性质
若$ f(n)$和 \(g(n)\) 都是积性函数,则以下函数也为积性函数:
\[\begin{aligned} & h(x) = f(x^p)\\ & h(x) = f^p(x)\\ & h(x) = f(x)g(x)\\ & h(x) = \sum_{d\mid x} f(d)g\left(\dfrac{x}{d}\right) \end{aligned} \]
积性函数的证明

P1403 [AHOI2005]约数研究(数据范围1e7)



艾佛森括号
\[[P] = \begin{cases} 1 &\text{If P is true}\\ 0 &\text{Otherwise} \end{cases} \]
此处 \(P\)是一个可真可假的命题。
整除分块
时间复杂度
时间复杂度\(O(\sqrt n)\),证明见下
引理
\[\forall a,b,c\in \mathbb{Z},\left\lfloor\dfrac{a}{bc}\right\rfloor = \left\lfloor{\dfrac{\left\lfloor\dfrac{a}{b}\right\rfloor}{c}}\right\rfloor \]
证明
\[\left\lfloor\dfrac{a}{bc}\right\rfloor = \left\lfloor\dfrac{a}{b}\times\dfrac{1}{c}\right\rfloor = \left\lfloor{\dfrac{1}{c}\times\left({\left\lfloor{\dfrac{a}{b}}\right\rfloor + r}\right)}\right\rfloor = \left\lfloor{\dfrac{\left\lfloor\dfrac{a}{b}\right\rfloor}{c} + \dfrac{r}{c}}\right\rfloor = \left\lfloor{\dfrac{\left\lfloor{\dfrac{a}{b}}\right\rfloor}{c}}\right\rfloor \]


关于右端点r的证明
\(首先,我们已经知道上一个端点的r,那我们现在的l=r+1,因此我们可以得到现在的值\)\(k=\left \lfloor \dfrac nl\right\rfloor\)
而\(\lfloor\frac{n}{l}\rfloor=\lfloor\frac{n}{r}\rfloor=k\)
实际上就是\(k \leq \frac{n}{l} \leq \frac{n}{r} < k+1\)
显然,我们需要找到一个r,使得\(r*k\leq n\),所以\(r=\left \lfloor \dfrac nk\right\rfloor\)
所以最终我们就有
\(r=\left \lfloor \dfrac {n}{\left \lfloor \dfrac nl\right\rfloor}\right\rfloor\)
例题一 H(n)
代码
#include<bits stdc++.h="">
using namespace std;
long long t,n,ans,l,r,k;
int main(){
cin>>t;
while(t--){
cin>>n;
r=0;
ans=0;
while(r+1<=n){
l=r+1;
k=n/l;
r=min(n,n/k);
ans+=k*(r-l+1);
}
cout<<ans<<endl; }="" return="" 0;="" ```="" ##="" [例题二="" p2261="" [cqoi2007]余数求和](https:="" www.luogu.com.cn="" problem="" p2261)="" ###="" 分析="" 对于这题而言,我们显然有="" $ans="\sum\limits_{i=1}^{n}k-i*\lfloor\frac{k}{i}\rfloor=n*k-\sum\limits_{i=1}^{n}i*\lfloor\frac{k}{i}\rfloor$" 所以我们只用分块计算$\sum\limits_{i="1}^{n}i*\lfloor\frac{k}{i}\rfloor$即可" 显然,对于其中的第一项$i$我们可以很好地进行计算,主要是后面的$\sum\limits_{i="1}^{n}\lfloor\frac{k}{i}\rfloor$我们要如何计算" 考虑我们已知$l$,求$r$,显然,当前的$num="\lfloor\frac{k}{l}\rfloor$" 而$\lfloor\frac{k}{l}\rfloor="\lfloor\frac{k}{r}\rfloor=num$,实际上就是$num" \leq="" \frac{k}{l}="" \frac{k}{r}="" <="" num+1$="" 因此就有$num="" \frac="" {k}{r}$,所以$r="" {k}{num}="" $,最终有$r="\lfloor\frac{k}{num}\rfloor" $="" 所以最终是$r="\left" \lfloor="" \dfrac="" {k}{\left="" kl\right\rfloor}\right\rfloor$,而不是$r="\left" {n}{\left="" kl\right\rfloor}\right\rfloor$="" 还有一个问题,当$num="0$时,求和项一定为0,所以我们不用去计算它的$r$,还要注意$r$要和$n$取$min$" 实际上我们还可以这样考虑:当$n\leq="" k="" $时,直接计算便可,当$n=""> k$时,$\lfloor\frac{k}{i}\rfloor=0$所以显然是$r=\left \lfloor \dfrac {k}{\left \lfloor \dfrac kl\right\rfloor}\right\rfloor$
### 代码
```cpp
#include<bits stdc++.h="">
#define int long long
using namespace std;
int n,k,l,r,num=0,ans=0;
signed main(){
cin>>n>>k;
r=0;
while(r+1<=n){
l=r+1;
num=k/l;
if(num==0)break;
r=min(n,k/(k/l));
ans=ans+(r+l)*(r-l+1)/2*num;
}
cout<<n*k-ans; return="" 0;="" }="" ```="" ##="" 扩展="" **分块的实质就是把能分块的求出来,然后剩下的项我们先预处理前缀和,然后计算贡献**="" 有时候我们要求形如$\sum\limits_{t="1}^{n}\left\lfloor\frac{n}{T}\right\rfloor\left\lfloor\frac{m}{T}\right\rfloor$的式子,实际上就是把相交的部分一起计算" 理论上时间复杂度最大为$o(4\sqrt="" n)$="" ###="" 代码="" ```cpp="" cin="">>n>>m;
if(n>=m)swap(n,m);
int l,r=0,num1,num2,r1,r2;
while(r+1<=n){
l=r+1;
num1=n/l,num2=m/l;
r1=n/num1,r2=m/num2;
r=min(n,min(r1,r2));
ans+=num1*num2*(sum_f[r]-sum_f[l-1]);
}
cout<<ans<<endl; ```="" #="" 莫比乌斯函数="" ="" me8rjsaj.png)="" f1bl0o7z.png)="" 莫比乌斯反演="" ~~**其实并没有什么用**~~="" ##="" 形式一="" 如果有="" $="" f(n)="\sum\limits_{d|n}g(d)$" 就有="" g(n)="\sum\limits_{d|n}" \mu(d)f(\frac{n}{d})$="" $这种形式下,数论函数f(n)称为数论函数="" 的莫比乌斯变换,数论函数="" g(n)称为数论函数="" f(n)的莫比乌斯逆变换(反演)。$="" 形式二="" \mu(\frac{d}{n})f(d)$="" 做题中最重要的公式="" 1、$="" [n="1]=\sum\limits_{d|" n}="" \mu(d)$="" **证明:**="" bwun89o3.png)="" 2、$="" n="\sum\limits_{d|n}\varphi(d)$" [**证明**](https:="" www.cnblogs.com="" xxzh="" p="" 9285771.html#:~:text="%E4%BB%BB%E4%BD%95%E6%AD%A3%E6%95%B4%E6%95%B0n%E7%AD%89%E4%BA%8E%E5%85%B6%E5%9B%A0%E6%95%B0%E7%9A%84%E6%AC%A7%E6%8B%89%E5%87%BD%E6%95%B0%E5%80%BC%E4%B9%8B%E5%92%8C%EF%BC%8C%E5%8D%B3%E2%88%91d%7Cn%CF%86,%28d%29%3Dn)" 设一个集合${1="" n,2="" n,3="" n,...,(n-1)="" n,n="" n}$="" 对于上述的分式集合,若我们都将其化简至最简形式,设其中一个最简形式是a="" b,那么我们一定有:="" $b|n="" $①="" $(a,b)="1$" ②="" $a<="b$" ③="" 由②③可得,对于一个确定的b,它对应的a的个数为$\varphi(b)$(根据欧拉函数的定义:φ(n)="1到n中与n互质的数的个数)" 那么我们再考虑,每一个最简形式a="" b都是互相不同的,因为它们都是最简形式="" 而且,对于上述分数集合来说每一个元素都可以化简成最简形式(完备性),而元素的个数正好就是n="" 于是定理得证="" 3、$\frac{\varphi(n)}{n}="\sum\limits_{d|n}\frac{\mu(d)}{d}$" 考虑证明该式子="" 欧拉函数的定义式$\varphi(n)="\sum\limits_{i=1}^{n}[gcd(n,i)=1]$" 莫比乌斯函数的求和式$="" 我们用$gcd(n,i)$代替$n$就有="" [gcd(n,i)="1]=\sum\limits_{d|gcd(n,i)}" 所以="" $$="" \begin{aligned}="" \varphi(n)="" &="\sum\limits_{i=1}^{n}[gcd(n,i)=1]\\" \mu(d)\\="" \\="" \lfloor="" \frac{n}{d}\rfloor\\="" \frac{n}{d}\\="" \end{aligned}="" 所以就有$\frac{\varphi(n)}{n}="\sum\limits_{d|n}\frac{\mu(d)}{d}$" 手推式子(默认$n\leq="" m$)="" 一些基础的东西="" 1、$[n|\gcd(a,b)]\iff[n|a][n|b]$="" 令$a="dp,b=dq$,其中$\gcd(p,q)=1$" 考虑证明充分性="" 当$n|\gcd(a,b)$时,就相当于$n|d$="" $[n|\gcd(a,b)]="[n|d]$" $[n|a][n|b]="[n|dp][n|dq]$" 若$[n|d]="1,则[n|dp][n|dq]=1$" \nmid="" d,若要使[n|dp][n|dq]="1,则要n\mid" 且n\mid="" q="" ,又因\gcd(p,q)="1,所以n=1,[n|d]=1,矛盾$" 所以充分性得证="" 考虑证明必要性="" 若有$[n|a][n|b],则有[n|dp][n|dq]$="" 若$n|d,则命题得证$="" 若$n\nmid="" d,则有[n|p][n|q],且[n|\gcd(a,b)]="0$" 若此时$[n|p][n|q]="1,则由\gcd(p,q)=1,有n=1,但此时[1|\gcd(a,b)]=1,矛盾$" 故得证="" 2、$f(x)="\sum\limits_{i=1}^{n}[x|i]=\lfloor" \frac="" nx="" \rfloor$="" 用人话来说就是求1到n中x的倍数,证明显然="" [例题一="" p3935="" calculating](https:="" www.luogu.com.cn="" problem="" p3935)="" 若$x$分解质因数的结果为$x="\prod\limits_{i=1}^{z}{p_i}^{k_i}$,令$f(x)=\prod\limits_{i=1}^{z}(k_i+1)$" 求$\sum\limits_{i="l}^{r}f(i)$对$998244353$取模的结果" 上面的可以简化为:="" ans="\sum\limits_{i=1}^{r}f(i)-\sum\limits_{j=1}^{l-1}f(j)" 考虑求="" \sum\limits_{i="1}^{n}f(i)&=\sum\limits_{i=1}^{n}\sum\limits_{j|i}1\\" \rfloor\\="" \rfloor="" 最后再数论分块即可。="" 时间复杂度="" $\mathcal="" o(\sqrt{n})$。="" [例题二="" p2260="" [清华集训2012]模积和](https:="" p2260)="" 求="" $$\sum_{i="1}^{n}" \sum_{j="1}^{m}" (n="" \bmod="" i)="" \times="" (m="" j),="" i="" \neq="" j$$="" mod="" 19940417="" 的值="" 首先不妨设$n<m$="" 注意到后面的$i="" j$,则可以将式子变成="" i)\times="" j)-\sum\limits_{i="1}^{n}(n" 然后显然就有="" \sum\limits_{j="1}^{m}(m" 根据取模的定义,$a="" b="a-b" \left\lfloor\frac{a}{b}\right\rfloor$,就有="" \left\lfloor\frac{n}{i}\right\rfloor)\times\sum\limits_{j="1}^{m}(m" -="" j="" \left\lfloor\frac{m}{j}\right\rfloor)-\sum\limits_{i="1}^{n}(n-i" \left\lfloor\frac{n}{i}\right\rfloor)\times(m-i\times="" \left\lfloor\frac{m}{i}\right\rfloor)="" 拆括号="" (n^2-\sum\limits_{i="1}^{n}i" \left\lfloor\frac{n}{i}\right\rfloor)\times(m^2-\sum\limits_{j="1}^{m}j" 例题三="" 考虑使用公式$="" \mu(d)$进行化简="" &\sum\limits_{i="1}^{n}\sum\limits_{j=1}^{m}[\gcd(i,j)=1]\\" &注意此时d的枚举范围并不影响结果\\="" &可以证明[d|\gcd(i,j)]的充要变换是[d|i][d|j]\\="" &观察到当d="[n+1,m]时式子为0,无意义\\" &所以上界取n即可\\="" 例题四="" 化简="" ###="" 方法一(采用欧拉函数):="" 方法二(采用莫比乌斯函数):="" &令i="da,j=db\\" \mu(k)\\="" [k|a][k|b]\mu(k)\\="" [k|b]\\="" &令l="kd\\" (l\sum\limits_{k|l}\frac{\mu(k)}{k})\\="" &实际上就是\\="" 例题五="" 方法:="" &使用例题四\sum\limits_{i="1}^{n}\sum\limits_{j=1}^{m}\gcd(i,j)=\sum\limits_{l=1}^{m}\varphi(l)\lfloor\frac{n}{l}\rfloor\lfloor\frac{m}{l}\rfloor的结论\\" &令dk="T\\" 例题六="" [p1829="" [国家集训队]crash的数字表格="" jzptab](https:="" p1829)="" 求(对="" 20101009="" 取模):="" 易得:="" \cdot="" j}{\gcd(i,j)}\\="" j}{d}[\gcd(i,j)="d]\\" db}{d}[\gcd(da,db)="d]\\" &令a="ik,b=jk\\" k^2\sum\limits_{i="1}^{\left\lfloor\frac{n}{kd}\right\rfloor}i\sum\limits_{j=1}^{\left\lfloor\frac{m}{kd}\right\rfloor}j\\" k^2\frac{(1+\left\lfloor\frac{n}{kd}\right\rfloor)\cdot="" \left\lfloor\frac{n}{kd}\right\rfloor}{2}\frac{(1+\left\lfloor\frac{m}{kd}\right\rfloor)\cdot="" \left\lfloor\frac{m}{kd}\right\rfloor}{2}\\="" &令t="kd\\" \left\lfloor\frac{n}{t}\right\rfloor}{2}\frac{(1+\left\lfloor\frac{m}{t}\right\rfloor)\cdot="" \left\lfloor\frac{m}{t}\right\rfloor}{2}\sum\limits_{k|t}\frac{t}{k}\mu(k)\cdot="" k^2\\="" \left\lfloor\frac{m}{t}\right\rfloor}{2}\sum\limits_{k|t}\mu(k)\cdot="" k\\="" 例题七="" 题目描述="" fhhqr99r.png)="" 分析="" 实际上这个就是例题五,重要的是我们要怎么处理最后的$$\sum\limits_{k|t}\mu(\frac{t}{k})f(k)$$="" 考虑如下操作="" &令g(t)="\sum\limits_{k|T}\mu(\frac{T}{k})f(k)\\" &显然g(1)="0\\" &我们分类讨论\\="" &1,t为质数时,g(t)="\mu(1)*f(T)+\mu(T)*f(1)=1\\" &令now="T*p,T=T'*p^{u+1}\\" &2,当t不为质数:\\="" &g(t*p)\\="" f(d)\\="" f(d)+\sum\limits_{d|t'}\mu(\frac{t'*p^{u+1}}{d*p^{u+1}})*="" f(d*p^{u+1})\\="" &此时由于后面的f(d*p^{u+1}),我们无法继续计算,因此我们考虑换一种思考方式\\="" &我们看回式子本身g(now)="\sum\limits_{k|now}\mu(\frac{now}{k})f(k),此时now不为质数,now=T*p\\" &我们可以让p="p_1,T=" p_1^{a_1-1}p_2^{a_2}="" \dots="" p_n^{a_n}="" ,k="p_1^{b_1}p_2^{b_2}" p_n^{b_n},\frac{t*p}{k}="p_1^{c_1}p_2^{c_2}" p_n^{c_n}\\="" &很显然,如果要对答案有贡献,那么c_i="0或1\\" &分类讨论:\\="" &1、如果对于任意的i\not="1,都有a_1+1<a_i,那么b_1是否为a_1+1都不会对f(k)产生影响,假设b_1=a_1时有f(k)的贡献,那么b_1=a_1+1时就有-f(k)的贡献,所以g(now)=0\\" &2、如果对于任意的i\not="1,都有a_1+1">a_i,那么b_1是否为a_1+1都不会对f(k)产生影响,假设b_1=a_1时有f(k)的贡献,那么b_1=a_1+1时就有-f(k)的贡献,所以g(now)=0\\
&3、如果对于任意的i\not=1,都有a_1+1=a_i,如果我们让若在b_1=a_1时贡献依然为f(k),且在b_1=a_1+1时看做有-f(k)的贡献时,就会发现在b_1=a_1+1,且b_i=a_i-1的时候,贡献会有1的差别\\
&原来的总贡献为0,若n为奇数,则\mu中有奇数个质因子,为-1,减去这个多出来的贡献就可以算出最终贡献为1
&因此,当now的质因子个数相同,且有偶数个质因子时,g(now)=-1\\
&有奇数个质因子时g(now)=1\\
&其余情况下g(now)=0\\
&剩下的做法就简单了
\end{aligned}
$$
### 代码
```cpp
#include<bits stdc++.h="">
#define int long long
using namespace std;
const int maxn=1e7+10,maxm=664579+10;
int g[maxn],gg[maxn],MAX[maxn],f[maxn],sum_f[maxn];
bool vis[maxn]={false};
int pri[maxm],cnt=0;
int T,n,m;
void init(){
g[1]=1;
gg[1]=1;
MAX[1]=0;
f[1]=-1;
sum_f[1]=0;
for(int i=2;i<=maxn;i++){
if(!vis[i]){
pri[++cnt]=i;
g[i]=i;
gg[i]=1;
MAX[i]=1;
f[i]=1;
// cout<<i<<" ";="" }="" for(int="" j="1;j<=cnt&&pri[j]*i<=maxn;j++){" int="" num="pri[j]*i;" vis[num]="true;" if(i%pri[j]="=0){" g[num]="pri[j]*g[i];" gg[num]="gg[i]+1;" max[num]="max(MAX[num/g[num]],gg[num]);" f[num]="(f[num/g[num]]!=0&&(gg[num]==MAX[num/g[num]]||num/g[num]==1))?(-f[num/g[num]]):0;" break;="" sum_f[i]="sum_f[i-1]+f[i];" cout<<i<<"="" "<<g[i]<<"="" "<<gg[i]<<"="" "<<max[i]<<"="" "<<f[i]<<endl;;="" return="" ;="" signed="" main(){="" cin="">>n>>m;
init();
cin>>T;
while(T--){
int ans=0;
cin>>n>>m;
if(n>=m)swap(n,m);
int l,r=0,num1,num2,r1,r2;
while(r+1<=n){
l=r+1;
num1=n/l,num2=m/l;
r1=n/num1,r2=m/num2;
r=min(n,min(r1,r2));
ans+=num1*num2*(sum_f[r]-sum_f[l-1]);
}
cout<<ans<<endl; }="" cout<<cnt<<endl;="" cout<<ans;="" return="" 0;="" ```="" ##="" 例题八="" [p3312="" [sdoi2014]数表](https:="" www.luogu.com.cn="" problem="" p3312)="" ###="" 代码="" ```cpp="" #include<bits="" stdc++.h="">
#define int long long
using namespace std;
const int maxn=1e5+10,maxm=664579+10,maxT=2*1e4+5;
int g[maxn],mu[maxn],ANS[maxn];
bool vis[maxn]={false};
int pri[maxm],cnt=0;
int TT,n,m;
struct edge{
int v,pos;
}f[maxn];
bool cmp2(edge x,edge y){
if(x.v==y.v)return x.pos<y.pos; return="" x.v<y.v;="" }="" void="" init(){="" mu[1]="1;" g[1]="1;" f[1].v="1;" f[1].pos="1;" for(int="" i="2;i<=maxn;i++){" if(!vis[i]){="" pri[++cnt]="i;" mu[i]="-1;" g[i]="i;" f[i].v="i+1;" cout<<i<<"="" ";="" j="1;j<=cnt&&pri[j]*i<=maxn;j++){" int="" num="pri[j]*i;" vis[num]="true;" if(i%pri[j]="=0){" mu[num]="0;" g[num]="g[i]*pri[j];" f[num].v="f[i].v+f[num/g[num]].v*g[num];" break;="" f[i].pos="i;" "<<g[i]<<"="" "<<f[i].v<<endl;;="" ;="" struct="" node{="" x,y,lim,pos;="" }a[maxn];="" bool="" cmp1(node="" x,node="" y){="" x.lim<y.lim;="" tree{="" tr[maxn];="" update(int="" now,int="" num){="" for(;now<="maxn;now+=now&(-now))tr[now]+=num;" check(int="" now){="" ans="0;" for(;now="">0;now-=now&(-now))ans+=tr[now];
return ans;
}
}T;
signed main(){
// cin>>n>>m;
init();
sort(f+1,f+maxn+1,cmp2);
// for(int i=1;i<=maxn;i++)cout<<f[i].pos<<" "<<f[i].v<<endl;="" cin="">>TT;
for(int i=1;i<=TT;i++){
cin>>a[i].x>>a[i].y>>a[i].lim;
a[i].pos=i;
if(a[i].x>a[i].y)swap(a[i].x,a[i].y);
}
sort(a+1,a+TT+1,cmp1);
int now=0;
for(int i=1;i<=TT;i++){
while(f[now+1].v<=a[i].lim){
now++;
// cout<</f[i].pos<<"></y.pos;></ans<<endl;></i<<"></bits></ans<<endl;></n*k-ans;></bits></ans<<endl;></bits>