双因素方差分析流程
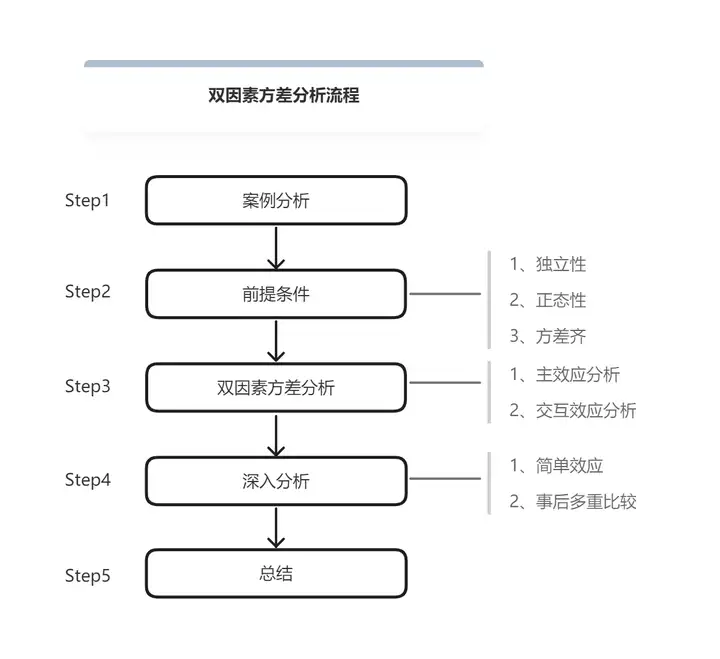
一、案例分析
当前收集了39名志愿者减重效果的相关数据,他们的生活方式可分为3种,现在研究人员想要研究生活方式和性别对于减重的影响,想要知道不同的生活方式和性别它们的减重效果之间是否具有显著性差异,收集的部分数据如下:
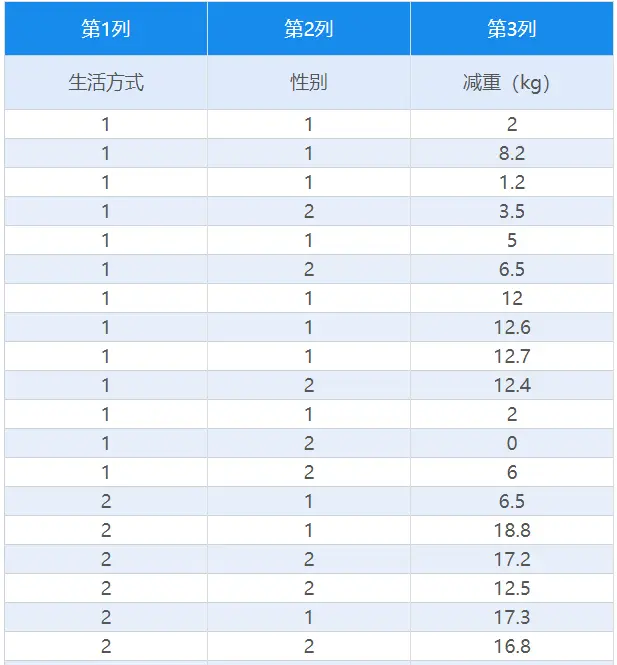
研究中的“生活方式”、“性别”均为定类数据,“减重”为定量数据,想要研究不同生活方式、不同性别下减重效果的差异性可以使用双因素方差分析进行。
二、前提条件
双因素方差分析用于研究2个定类数据与定量数据之间的关系情况,但是使用双因素方差分析有三个前提条件,分析的数据需要满足独立性、正态性和方差齐性。接下来需要逐个进行检验,判断是否能够使用双因素方差分析进行研究。
(1)独立性
由于39名志愿者之间减重过程中相互独立、互不干扰,所以独立性检验通过。
(2)正态性
正态性检验的方法有很多种,常见的方法有统计检验法、图示法(直方图、P-P图、Q-Q图)等,其中统计检验法最为严格,故此次分析使用该方法进行正态性检验。
首先对不同组别减重效果进行正态性检验,SPSSAU正态性检验结果如下:

SPSSAU正态性检验共提供Kolmogorov-Smirnov检验、Shapiro-Wilk检验、Jarque-Bera检验三类正态性检验结果。因为本次分析样本量较小(<50),故使用Shapiro-Wilk检验结果进行判断。从上表可以得到,不同组别对应p值均大于0.05,说明数据具有正态性特征,通过正态性检验。如果样本量较大时,可以使用其他两种方法进行检验。
不同性别正态性检验结果如下:

从上表分析结果可知,不同性别下减重效果也通过正态性检验,综上,本案例数据通过正态性检验。接下来进行方差齐检验。
(3)方差齐
方差齐检验可以使用SPSSAU方差分析中的方差齐进行分析。不同生活方式减重效果的方差齐分析SPSSAU操作如下:
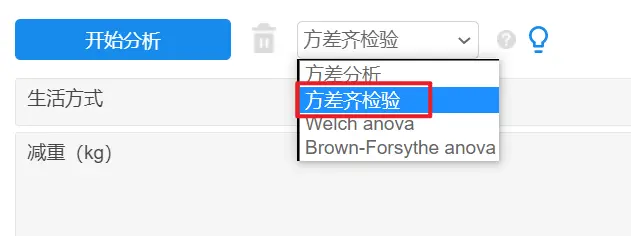
SPSSAU输出结果如下:

使用方差齐检验分析不同生活方式下减重效果的数据波动情况是否有显著差异,从上表可以看出:不同生活方式下减重效果均不会表现出显著性差异(p>0.05),即不同生活方式样本数据的波动性均呈现出一致性,并没有差异性,数据通过方差齐检验。
同上,对不同性别样本减重效果进行方差齐检验,得到结果如下:

从上表可知,不同性别样本数据的波动性也呈现出一致性,数据通过方差齐检验。综上,本案例数据通过方差齐检验。
综上,案例数据满足双因素方差分析的三个前提条件,可以进行双因素方差分析。
三、双因素方差分析
在进行双因素方差分析过程中,可以分别针对主效应和交互效应进行分析。主效应是指单独的自变量X对因变量Y的影响的差异;交互效应是指X1和X2的交互项X1*X2对Y的影响的差异。
(1)主效应分析
进行某因素的主效应分析时,即排除分析项之外的所有因素的干扰,比如在本案例中,主效应即为分别判断“生活方式”和“性别”对于减重的影响。
SPSSAU双因素方差分析结果如下:
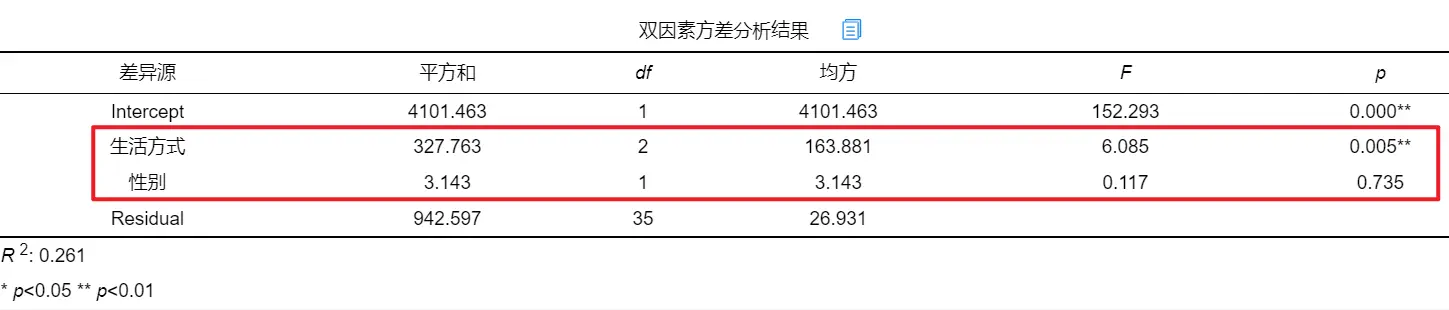
从上表可以看出,生活方式呈现出显著性(p<0.05),说明主效应存在,即不同生活方式会对减重产生差异影响。而性别没有呈现出显著性(p=0.735>0.05),说明性别不具有主效应,即不同性别并不会对减重产生差异影响。接下来查看生活方式与性别的交互项是否会对减重产生新的差异影响。
(2)交互效应分析
交互效应是研究不同自变量之间相互搭配是否会对因变量产生新的影响,例如本例中查看“生活方式*性别”对于减重的影响。如果要查看交互效应,需要在分析时勾选【二阶效应】(也称交互效应),如下图:
SPSSAU输出交互效应分析结果如下:
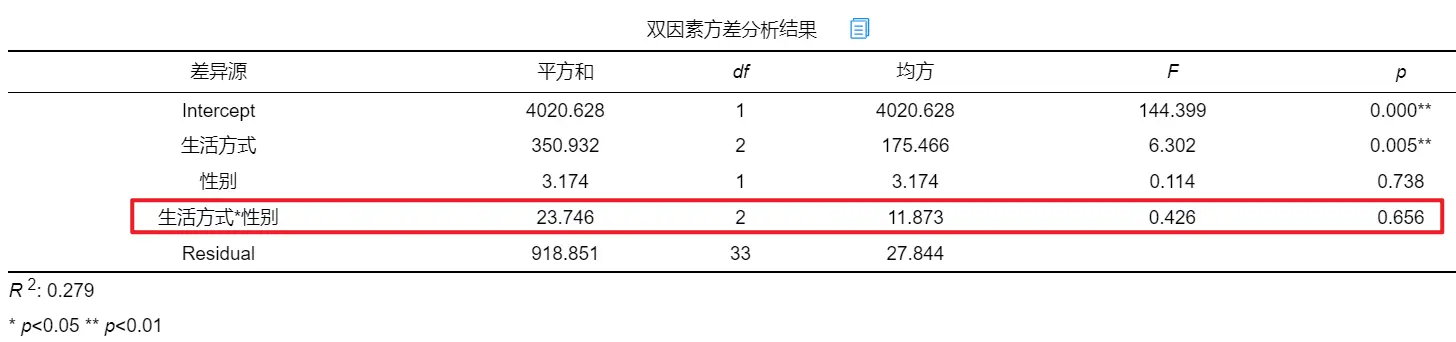
从上表可以看出,交互项“生活方式*性别”并没有呈现出显著性(p=0.656>0.05),说明不存在交互效应。
综上所述,本次分析生活方式会对减重产生显著差异影响,性别不会对减重产生显著差异影响,且不存在交互效应。接下来进行进一步分析。
四、深入分析
对于双因素方差分析,如果交互效应存在,可以进一步进行简单效应分析。简单效应是指自变量X1在某水平时,自变量X2不同水平之间的差异比较。而当主效应存在是,可以进行事后多重比较。事后多重比较是指存在主效应的自变量X,其不同水平两两之间的差异对比。
(1)简单效应
本案例中交互效应不存在,所以一般不进行简单效应分析。为做讲解使用,使用分析结果进行简单效应分析说明。本案例中,举例说明简单效应分析如:当生活方式为1时,研究不同性别之间减重的差异;或当性别为1时,生活方式为1和2的二者之间减重的差异。
当交互效应存在时,进行简单效应分析,在分析时勾选【简单效应】,如下图:
此时SPSSAU会输出简单效应分析结果,如下图:

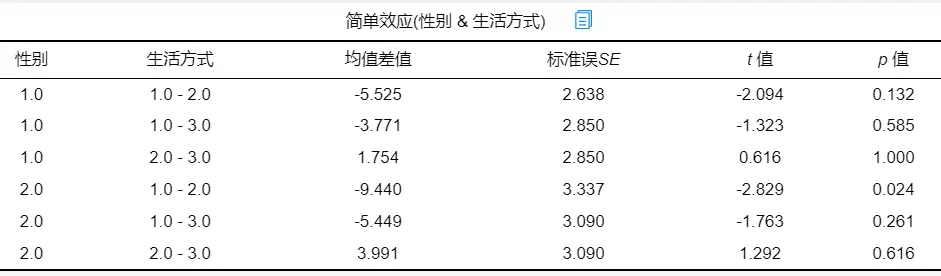
如果交互效应存在,那么可以查看简单效应分析对应的p值,查看具体生活方式与性别组合下的减重差异。由于本例交互效应不存在,故不再进行说明。接下来进行事后多重比较。
(2)事后多重比较
本例中,生活方式的主效应存在,可以进行事后多重比较,比较不同生活方式两两之间减重的差异情况。事后多重比较的方法有很多种,常见的有LSD法、Scheffe法、Tukey法、Bonferroni校正法等等,因为LSD法使用最为广泛,检验效能较高,所以本案例使用该方法进行事后多重比较。SPSSAU操作如下:
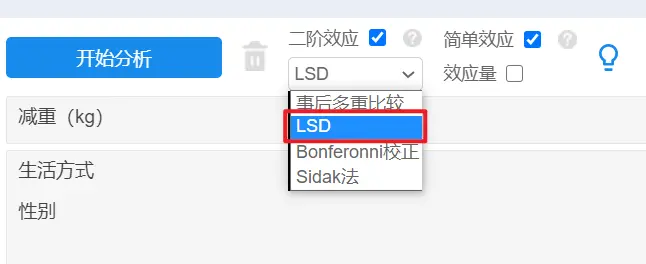
SPSSAU输出结果如下:

从上表可以看出,针对生活方式进行事后多重比较,生活方式1和生活方式2之间呈现出显著性差异(p=0.001<0.05);生活方式1和生活方式3之间呈现出显著差异(p=0.035<0.05);而生活方式2和生活方式3之间并没有呈现出显著性差异(p=0.181>0.05)。具体对比均值差值,可以看出生活方式2的均值最大,即说明生活方式2的减重效果最好。
因为性别的主效应并不存在,故不进行事后多重比较。
五、总结
使用双因素方差分析研究不同生活方式、不同性别对于减重的影响是否存在差异;研究发现生活方式对减重有显著性影响,而性别对于减重并没有显著影响,且生活方式和性别二者交互效应不存在。利用事后多重比较深入分析不同生活方式之间的差异,研究得到,生活方式2的减重效果最好。所以如果想要得到更好的减重效果,可以按照生活方式2进行减重。
标签:减重,交互,流程,因素,效应,方差分析,检验,性别 From: https://www.cnblogs.com/spssau/p/17266270.html