AHP层次分析法分析流程:
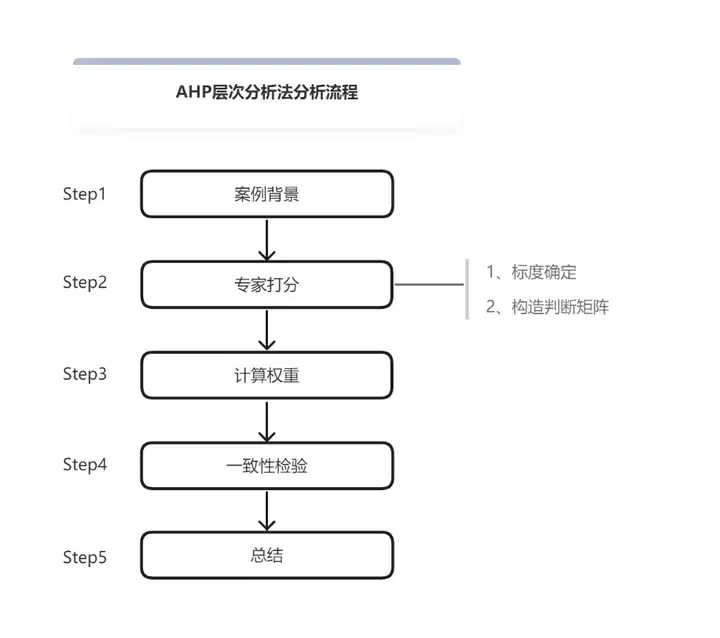
一、案例背景
当前有一项研究,想要构建公司绩效评价指标体系,将一级指标分为4个,分别是:服务质量、管理水平、运行成本、安全生产,现在想要确定4个指标的权重。
AHP层次分析法是一种主观赋权法和客观赋权法相结合的方法,近年来,被广泛应用于指标权重的确定。该方法将定量分析和定性分析方法结合,先用专家经验判断指标相对重要程度,再计算权重,比较适合解决难以用定量方法应对的问题。因此本案例使用AHP层次分析法进行4个指标权重的确定。
二、专家打分
AHP层次分析法通过专家打分,确定各个指标之间的相对重要程度。此步骤包括两部分内容,分别是判断指标重要程度的标度确定,以及根据专家打分构造判断矩阵。
- 标度确定
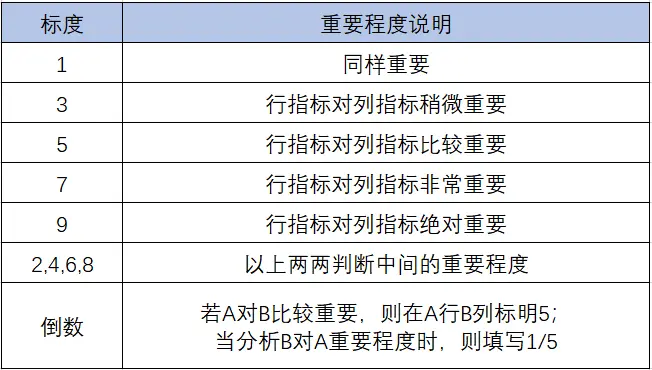
多位专家将各个指标进行相互比较后,使用一个判断值来表示相对重要程度,常见的标度法有1-5分标度法(最低为1分,最高为5分),和1-9分标度法(最低为1分,最高为9分).本案例使用1-9分标度法,取值说明如下表:
- 构造判断矩阵
当前共有20位专家对4个指标进行打分,采用1-9分标度法,将20位专家的打分进行计算平均分,得到最终判断矩阵表格,如下表:
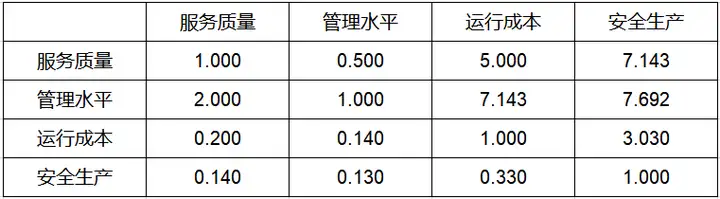
上表格显示,管理水平相比于服务质量一般重要,为2分;相反服务质量相比于管理水平来讲,则为0.5分。运行成本相比于服务质量不太重要,为0.2分;相反,服务质量相比于运行成本比较重要,则为5分。其余指标相对重要程度解读也类似。
判断矩阵构造完成后,接下来就可以进行权重计算。
三、计算权重
计算权重需要依次计算特征根、最大特征根值、最后得到一致性指标CI值,用于下一步一致性检验使用。计算过程如下:
① 判断矩阵每一行元素的乘积:
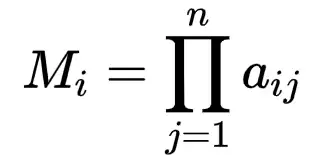
上式中 aij第i个元素与第j个元素的关系比值。
② 计算Mi的n次方根:
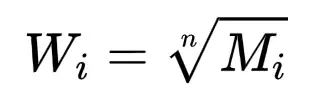
③ 对向量进行归一化处理:
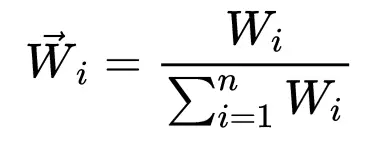
④ 计算判断矩阵的特征根:
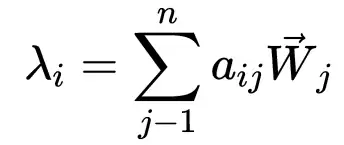
⑤ 计算判断矩阵的最大特征根:

⑥ 计算一致性指标CI值:
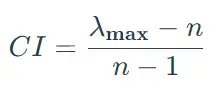
在实际研究中,计算过程比较复杂,使用SPSSAU软件计算即可。在SPSSAU系统中,选择AHP层次分析法,将判断矩阵填写完成,如下图:
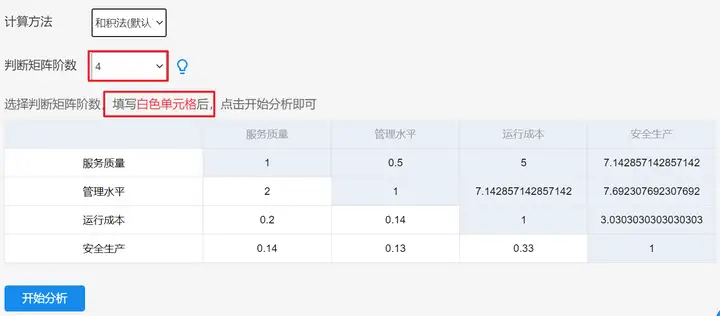
提示:SPSSAU只需要填写白色单元格,蓝色单元格会自动变化。
得到AHP层次分析结果如下表:

从上表可以得到,服务质量、管理水平、运行成本、安全生产4个指标使用AHP层次分析法计算权重(计算方法为:和积法),分析得到特征向量为(1.332,2.102,0.374,0.193);得到权重值分别为33.29%、52.54%、9.35%、4.82%;结合特征向量计算出最大特征根为4.139;接着利用最大特征根值计算得到CI值为0.046【CI=(最大特征根-n)/(n-1)】,CI值用于下述的一致性检验使用。
四、一致性检验
在构造判断矩阵时,有可能会出现逻辑错误,比如A比B重要,B比C重要,但是又出现C比A重要的情况,因此需要进行一致性检验。一致性检验使用一致性比率CR值进行分析。CR值小于0.1说明数据通过一致性检验,反之没有通过。
CR=CI/RI,CI值在上一步已经得到,为0.046,RI值直接通过查表得到,RI指标见下表:

本案例为4阶(4个指标),找到对应RI值为0.89,进行一致性检验,结果如下:

从上表可知,CR值=0.052<0.1,所以本次研究案例通过一致性检验,计算所得权重具有一致性。如果未通过一致性检验,需要检查判断矩阵是否存在逻辑问题,如果存在,则重新录入判断矩阵后再次进行分析。
五、总结
AHP层次分析法为定量分析与定性分析相结合的权重计算方法,通过专家打分,构造判断矩阵后,使用AHP层次分析法计算得到服务质量、管理水平、运行成本、安全生产4个指标的权重分别为:33.29%、52.54%、9.35%、4.82%。同时AHP层次分析法需要进行一致性检验,检验判断矩阵是否存在逻辑问题。经过计算,CR值小于0.1,通过一致性检验,说明判断矩阵不存在逻辑问题,计算权重具有科学性。
参考文献:
城镇污水处理厂绩效评价研究_魏星星
整体托管煤矿安全管理水平评价研究_张建强
标签:指标,流程,矩阵,分析法,AHP,计算,一致性 From: https://www.cnblogs.com/spssau/p/17265962.html