正态分布说明
正态分布在统计学中是一个很重要的概率分布类型,哪怕是在实际生活中也有着重要的指导与应用作用,比如:某学校学生的成绩分布,男子身高、工厂生产产品的尺寸等等。同时,正态分布也是许多检验的基础,在实际使用统计分析时,人们总是乐于正态检验。比如F检验以及t检验等在总体不是正态分布时一般没有意义。所以检验数据是否服从正态分布一直都是统计学比较重要的问题。所以本篇文章分别进行对检验正态分布的方法进行说明。
检验正态分布方法
检验数据是否服从正态分布的方法有很多,常用的有正态性检验(S-W检验、K-S检验),查看峰度与偏度以及图示化(直方图、p-p/q-q图)等。接下来一一说明。
正态性检验
正态性检验顾名思义判断总体是否服从正态分布的检验。它是统计判决中重要的一种特殊的拟合优度的假设检验。SPSSAU提供的正态性检验方法有三个如下:

针对三种正态性检验方法的区别如下:
S-W检验检验一般需要样本量小于50,如果样本量大于50建议使用K-S检验,J-B检验基于数据样本的偏度(统计数据分布偏斜方向和程度的度量)和峰度分析(表征概率密度分布曲线在平均值处峰值高低的特征数),一般用于大样本分析。正态性检验属于非参数检验,原假设为“样本来自的总体与正态分布无显著差异就符合正态分布”,即当p<0.05是拒绝原假设,数据不符合正态分布,p>0.05是接受原假设,数据符合正态分布。接下来进行查看
‘峰度和偏度’如何进行数据正态分布的检验。
偏度和峰度
偏度也称偏斜度,描述数据分布的偏斜程度和方向,峰度描述数据分布曲线陡峭平缓程度的统计量,理论上讲,标准正态分布偏度和峰度均为0,但现实中数据无法满足标准正态分布,因而如果峰度绝对值小于10并且偏度绝对值小于3,则说明数据虽然不是绝对正态,但基本可接受为正态分布。【参考文献:Kline R , Kline R B , Kline R . Principles and Practice of Structural Equation Modelling[J]. Journal of the American Statistical Association, 2011, 101(12).】。除此之外,还有图示化可以进行验证,比如直方图、p-p/q-q图。
图示化
除了用正态性检验和偏度和峰度的方法,还可以结合图形进行分析数据是否符合正态分布。其中包括直方图和p-p/q-q图。
直方图
如果使用直方图,直方图若呈现‘中间高,两边低,左右基本对称的钟形图’则基本服从正态分析,但是数据量过少等也可能影响结果导致很难呈现出标准的正态分布,如果是这种情况如果看见‘钟形’也可以接受的。比如:
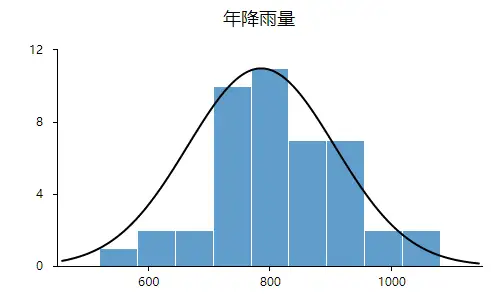
上图可以看出,数据呈现的分布并不是很对称,但是也出现近似‘钟形’曲线,所以也可以勉强接受。
p-p/q-q图
p-p图和q-q图都是根据累计分布函数理论计算的,使用它们可以进行数据是何种分布的检验,但是常用于检验数据是否服从正态分布。如果图形中所有店都聚集在直线上,则说明变量分布服从于所要检验的分布,直观说法就是如果散点分布近似‘对角线’则可以认为正态分布。比如:
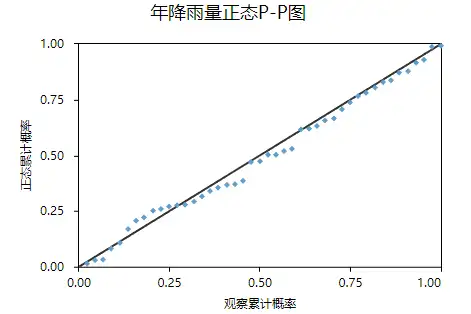
从上图可以看出散点分布近似‘对角线’则可以认为正态分布。q-q图也是如此。
几种方法说明
上述展示几种正态检验的方法,大体可以分为正态性检验,偏度与峰度以及图示化三种,其中正态性检验要求最为严格,但是从实用性角度,正态性检验远不如偏度与峰度以及图示化这俩种实用,有时常常会出现这样的结果,明明数据偏度绝对值小于3峰度绝对值小于10,或者p-p图呈现近似“对角线”的结果,但是正态性检验并不通过。此时建议不要对正态性检验过于依赖,因为正态性检验要求严格通常无法满足,所以在分析中可以使用其它两种方法辅助进行判断。
举例正态检验
前面已经提到过方差等需要数据服从正态分布,所以接下来进行举例说明,比如想要研究不同品牌洗发水的销量情况。已知需要使用方差分析,现在想要查看数据是否服从正态分布。此例子中使用直方图进行判断。结果如下:
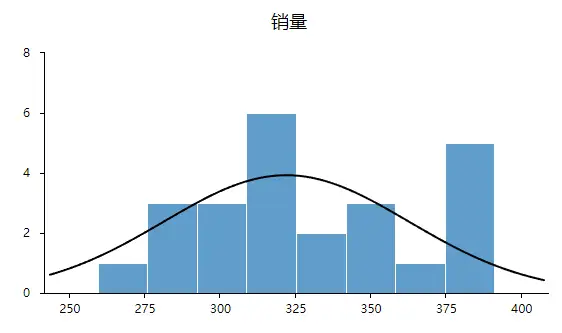
从上图中可以看出,“销量”数据直方图呈现‘中间高,两边低,并且左右基本对称的钟形图’则基本服从正态分析。所以可以进行后续分析。
总结
本篇文章主要对数据进行检验是否服从正态分布,检验正态分布的数据概括成三个一个正态性检验,一个是利用偏度和峰度进行说明,还有一种是图示化来表示,其中正态性检验条件最为严格,但是从实用性角度来看,却不如其它两种,如果在实证分析中,可以利用偏度与峰度和图示化进行辅助判断。
标签:偏度,流程,检验,直方图,峰度,正态性,正态分布 From: https://www.cnblogs.com/spssau/p/17266099.html