\(\color{purple}\text{P6348 [PA2011]Journeys}\)

\(\color{green}\text{2023.1.10 10:58}\)
线段树优化建边。
题意：给定一个图，每次对区间 \([a,b]\) 至区间 \([c,d]\) 建边。如果你很蠢，之间暴力建边，那么边复杂度是 \(O(n^2)\) ；如果你聪明一点，对每种边新建两个端点，那么 \([a,b]\) 连起点，\([c,d]\) 连终点，复杂度为 \(O(n)\) ；如果你想通过这道题，那就要用到线段树建边，假设每个点都已经连向某个区间了，那么你只要对区间建边即可。套用线段树，复杂度 \(O(\text{log n})\) 。

具体实现：

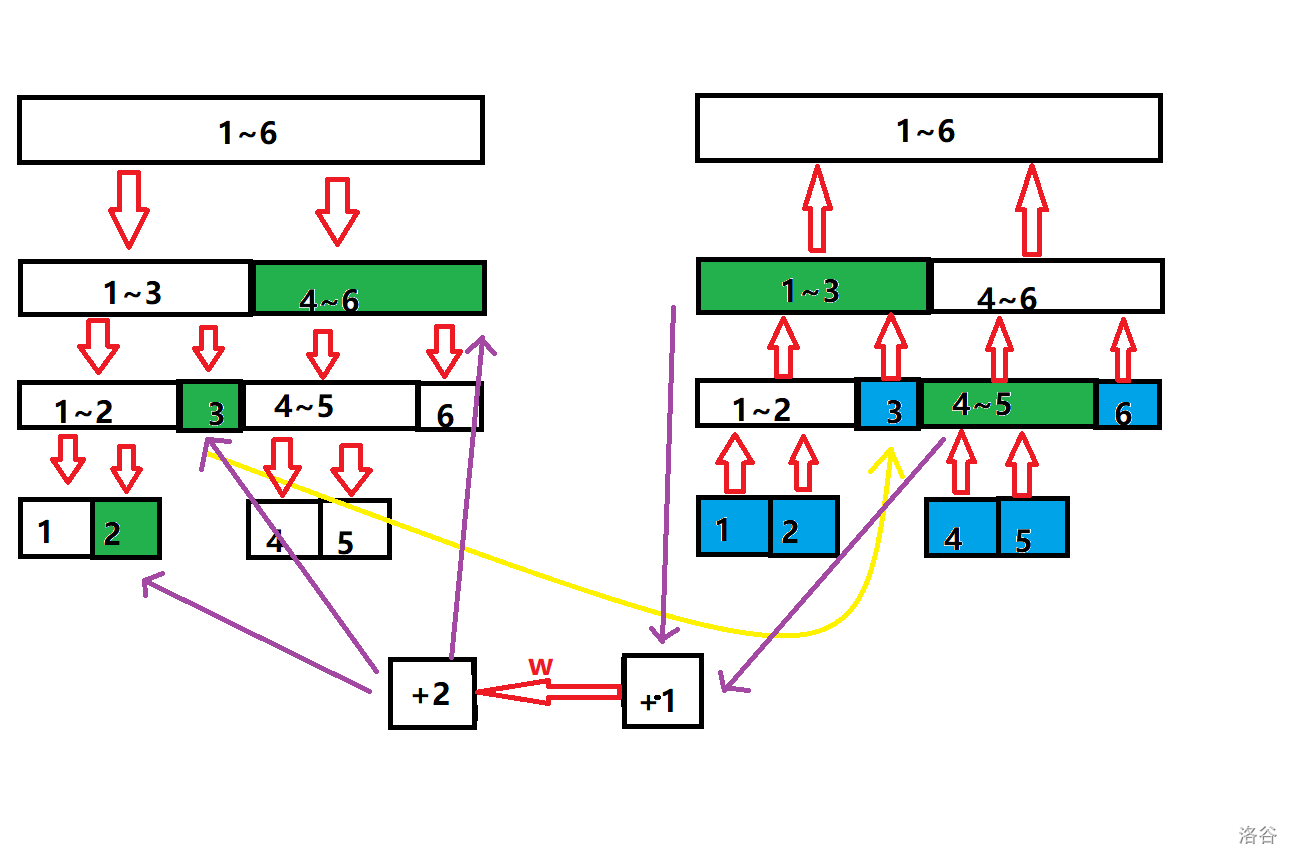
在这个例子中，给定 \(6\) 个点，对 \([1,5]\) 到 \([2,6]\) 建单向边。

真实的点是图中的蓝色点，而真实的边是图中的 \(w\) 边。（其他都是辅助点和边）

如图右边构成了一棵“入树”，其中的每个区间，是对应真实点可以到达的，
如图左边构成了一棵“出树”，其中的每个区间，能到达对应真实点。
（出树的叶子节点连向对应的真实点，即图中的黄边）（图中只标出了“3号点”的黄边，其他省略）。

建边：
首先新建这条边的两端点。（“+1点”和“+2点”）。
然后把入树上的 \([1,5]\) 连向“+1”。
然后把“+2”连向出树上的 \([2,6]\) 。
然后恭喜你学会了“\(\color{red}\text{线段树优化建边}\)”。

建完图后，发现真实边权为 \(1\) ，辅助边权为 \(0\) 。那么使用 \(\color{red}\text{01bfs}\) 求最短路最佳。