标签：plt eig 机器人 mu matmul 课后 np 习题 sigma

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from matplotlib.patches import Circle

第一题

第1问

为了方便，把状态记为\(x\)，位移、速度、加速度分别记为\(s\)、\(v\)、\(a\)。

状态向量为\([s_t,v_t]^T\)，状态转移矩阵为

\[A=\begin{bmatrix} 1&1\\ 0&1\\ \end{bmatrix} \]

第2问

控制量\(u_t\)设为0。近似认为单位时间内速度与加速度都是恒定值，则有

\[\begin{aligned} &s_{t+1}=s_t+v_{t}+\frac{1}{2}a_{t}\\ &s_{t+1}=v_{t}+a_{t} \end{aligned} \]

写成矩阵的形式有

\[x_{t+1}=Ax_{t}+\begin{bmatrix}\frac{1}{2}\\1\end{bmatrix}a_t \]

进一步可有定义以计算协方差矩阵\(R\)：

\[\begin{aligned} R&=\begin{bmatrix} Cov(\frac{1}{2}A_t)&E([\frac{1}{2}A_t-0][A_t-0])\\ E([\frac{1}{2}A_t-0][A_t-0])&Cov(A_t) \end{bmatrix}\\ &=\begin{bmatrix} \frac{1}{4}&\frac{1}{2}[Cov(A_t)+E(A)^2]\\ \frac{1}{2}[Cov(A_t)+E(A)^2]&1 \end{bmatrix}\\ &=\begin{bmatrix} \frac{1}{4}&\frac{1}{2}\\ \frac{1}{2}&1 \end{bmatrix} \end{aligned} \]

可以发现这个结果就是\([1,\frac{1}{2}]^T[1,\frac{1}{2}]\)，但是我概率论知识不扎实，不知道为什么可以这样算。
最后仿照3.4式可以写出状态转移概率

\[p(x_t\mid u_t,x_{t-1})=(2\pi R)^{-\frac{1}{2}}\exp\left[ (x_t-Ax_{t-1})^TR^{-1}(x_t-Ax_{t-1}) \right] \]

第3问

此时未作测量，只能计算先验估计，关系如下：

\[\begin{aligned} &\bar\mu_t=A\bar\mu_{t-1}\\ &\bar\Sigma_t=A\bar\Sigma_{t-1}A^T+R \end{aligned} \]

初始条件为\(\bar\mu_0=[0],\bar\Sigma=[0]\)，故不难知道均值始终为\([0]\)，只计算方差如下：

A = np.array([[1, 1], [0, 1]])
R = np.array([[1/4, 1/2], [1/2, 1]])
covar = np.zeros((2, 2))
ITER = 5

for i in range(ITER):
    covar = np.matmul(np.matmul(A, covar), A.T) + R
    print(covar)

[[0.25 0.5 ]
 [0.5  1.  ]]
[[2.5 2. ]
 [2.  2. ]]
[[8.75 4.5 ]
 [4.5  3.  ]]
[[21.  8.]
 [ 8.  4.]]
[[41.25 12.5 ]
 [12.5   5.  ]]

第4问

x_plot = []
y_plot = []
for theta in np.linspace(0, 2*np.pi, 100):
    u = np.array([[np.cos(theta)], [np.sin(theta)]])
    sig = np.matmul(np.matmul(u.T, covar), u)
    x_plot.append(np.sqrt(sig) * np.cos(theta))
    y_plot.append(np.sqrt(sig) * np.sin(theta))

eig, eig_vecs = np.linalg.eig(covar)
print("eigen value is %.4f and %.4f"%(eig[0], eig[1]))
print("corresponding sigma^2 is %.4f and %.4f"
    %(np.matmul(np.matmul(eig_vecs[:, 0].T, covar), eig_vecs[:, 0]), 
    np.matmul(np.matmul(eig_vecs[:, 1].T, covar), eig_vecs[:, 1])))
plt.arrow(0, 0, eig_vecs[0, 0] * np.sqrt(eig[0]), eig_vecs[1, 0] * np.sqrt(eig[0]),
    width=0.1, head_width=0.3, length_includes_head=True, color='red')
plt.arrow(0, 0, eig_vecs[0, 1] * np.sqrt(eig[1]), eig_vecs[1, 1] * np.sqrt(eig[1]),
    width=0.1, head_width=0.3, length_includes_head=True, color='purple')

plt.scatter(x_plot, y_plot, 2)
plt.grid()
plt.gca().set_aspect('equal')
plt.show()

eigen value is 45.1424 and 1.1076
corresponding sigma^2 is 45.1424 and 1.1076

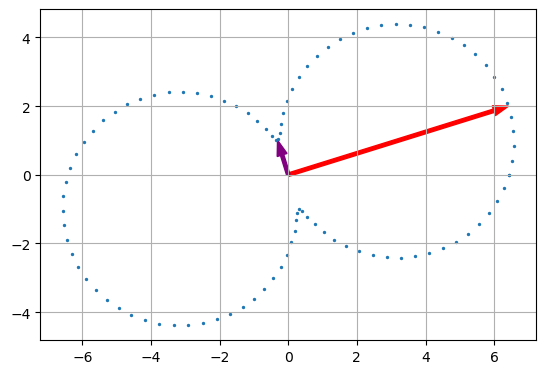
然而这个东西（每个方向上一个数据点投影后的标准差）并不是椭圆

标签：plt,eig,机器人,mu,matmul,课后,np,习题,sigma
From： https://www.cnblogs.com/harold-lu/p/16704434.html