FFT快速傅里叶变换<NTT
FFT和NTT是 \(O(nlogn)\) 处理两个多项式相乘的算法(FFT<NTT)
前置知识
复数
一个复数可以表示为
\[z=a+ib~~a,b\in R \]我们把他看做平面上的一个点,横轴代表实数部分,纵轴代表虚数部分
这个点就是 \((a,b)\)
我们把它放在极坐标上
[没事,不会极坐标这里有](极坐标系 - 知乎 (zhihu.com))
令\(\theta = \arctan{\frac a b} , x=\sqrt {a^2+b^2}\)
那么这个点就是 \((x,\theta)\)
则有
\[a=x\cos{\theta},~~b=x\sin{\theta} \]虚数变为了
\[z=x\cos{\theta}+ix\sin{\theta}=x(\cos\theta+i\sin\theta) \]由欧拉公式得(欧拉公式)
\[z=xe^{i\theta} \]这样任意一个虚数可以表示成这样
以上是复数前置知识
正式FFT
单位根
下文中,默认\(n\) 为 \(2\) 的正整数次幂
在复平面上,以原点为圆心,\(1\) 为半径作圆,所得的圆叫单位圆。以圆点为起点,圆的 \(n\) 等分点为终点,做 \(n\) 个向量,设幅角为正且最小的向量对应的复数为 \(\omega_n^0\) ,称为 \(n\) 次单位根,n代表长度。
根据复数乘法的运算法则,其余 \(n−1\) 个复数为 \(\omega_n^1,\omega_n^2,…,\omega_n^{n-1}\)
上面是我在别的地方看到的内容,学习FFT的时候我一直不太懂上面的部分,我今天用一个更加简单的方式让大家理解这部分内容
我们本来的多项式是这样的:
\[A(x)=c_0+c_1x+c_2x^2+…+c_nx^n \]因为复数\(\omega\)有一些特殊性质,我们需要用,并且我们把 \(x\) 直接替换 \(\omega\) 是没有关系的
所以就变成了:
\[A(\omega)=c_0+c_1\omega+c_2\omega^2+…+c_n\omega^n \]\(\omega_1,\omega_2,\omega_3,...,\omega_n\)不是一样的数,下面的n代表当前数列长度,算法里面不同时候用不同的,这个和他的性质有关系。
说了这么久 \(\omega\) 的性质,到底是什么性质呢?
通过欧拉定理
\[\omega_{n}^{k}=\cos\ k \frac{2\pi}{n}+i\sin k\frac{2\pi}{n} \]证明一些单位根性质,下面需要用
\(1.\omega_n^0=\omega_n^n=1\)
这显而易见。
\(2.\omega_n^{k+\frac n 2}=-\omega_n^k\)
证明:
\(3.\omega_{2n}^{2k}=\omega_n^k\)
证明:
\[\omega_{2n}^{2k}= \cos 2k \frac{2\pi}{2n}+i\sin 2k\frac {2\pi} {2n} =\cos k\frac {2\pi} n+i\sin k\frac {2\pi} n =\omega_{n}^k \]\(4.\sum_{i=0}^{n-1}(\omega_n^k)^i=0\)
证明:
第一步是根据等比数列求和公式:
下面我们把多项式每个系数放进一个数列里面
\[c_0+c_1x+c_2x^2+...+c_nx^n \rightarrow ~~ <c_0,c_1,c_2,...,c_n> \]傅里叶变换(学名不重要)
定义一个函数 \(h\) 表示
\(h(\omega_n^k)=c_0+c_1\omega^k+c_2\omega^{2k}+...+c_{n-1}\omega^{n-1}\)
这个函数其实有一个学名叫某数列的k次离散傅里叶级数,但不重要,草履虫不需要了解这些
这里和多项式乘法终于有关系了!
我们把两个多项式和他们乘起来的答案都先转换成数列
\[a_0+a_1x+a_2x^2+...+a_nx^n \rightarrow ~~ <a_0,a_1,a_2,...,a_n> \]\[b_0+b_1x+b_2x^2+...+b_nx^n \rightarrow ~~ <b_0,b_1,b_2,...,b_n> \]\[a_0b_0+(a_0b_1+a_1b_0)x+(a_0b_2+a_1b_1+a_2*b_0)x^2+... \rightarrow ~~ <a_0b_0,a_0b_1+a_1b_0,a_0b_2+a_1b_1+a_2b_0,...,> \]分别写出这两个数列的k次离散傅里叶级数的 h 函数
如果我们把两个玩意儿分别乘起来会惊奇的发现:
\[h_a(\omega_n^k)*h_b(\omega^k)=(a_0\times b_0)+(a_1\times b_0+a_0\times b_1)\omega^k +(a_2\times b_0+a_1\times b_1+a_0\times b_2)\omega^2k+... \]和\(h_{ab}(\omega^k)\)一模一样!!!
所以我们的步骤就变成了这样

那我们应该如何在\(O(nlogn)\)的复杂度内算出 \(h\) 函数呢?
求 \(h()\)
\[h(x)=c_0+c_1x+c_2x^2+...+c_{n-1}x^{n-1} \]我们把h函数分成偶数项和奇数项两部分
\[h_{0}(x)=c_0+c_2x+c_4x^2+...+c_{n-2}x^{\frac n 2-1} \]\[h_{1}(x)=c_1+c_3x+c_5x^2+...+c_{n-1}x^{\frac n 2-1} \]\[h(x)=h_{0}(x^2)+xh_{1}(x^2) \]\[h(\omega_n^k)=h_{0}(\omega_n^{2k})+\omega_n^k h_{1}(\omega_n^{2k}) \]通过可以推出\(\omega_{2n}^{2k}=\omega_n^k\)
\( h(\omega_n^k)=h_{0}(\omega_{\frac n 2}^{k})+\omega_n^k h_{1}(\omega_{\frac n 2}^{k}) \)
同理,将 \(\omega_n^{ k+\frac n2}\) 代入得
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_n^{ 2k+n})+\omega_n^{k+\frac n2}h_1(\omega_n^{ 2k+n})\)
因为\(\omega_n^{k+\frac n2}=-\omega_n^{k}\)
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_n^{2k}\omega_n^{n})-\omega_n^{k}h_1(\omega_n^{2k}\omega_n^{n})\)
因为\(\omega_n^n=1\)
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_n^{2k})-\omega_n^{k}h_1(\omega_n^{2k})\)
\(h(\omega_n^{ k+\frac n2})=h_0(\omega_{\frac n2}^{k})-\omega_n^{k}h_1(\omega_{\frac n2}^{k})\)
发现 \(h(\omega_n^{k})\) 和 \(h(\omega_n^{ k+\frac n2})\) 刚好是一加一减
我们在枚举第一个式子的时候也可以求出第二个式子的值啦
\(n\) 代表当前数列长度,每次减半,所以是\(log(n)\)
你是不是还是脑子里依托浆糊,我们来搞一个例子推一下(一个大括号里的前一个式子是我们需要的式子,后一个是顺便求出的)
假设我们求\(h(\omega_8^1)\)这个数列一共八位
\[\begin{cases} h(\omega_8^1)=h_0(\omega_4^1)+\omega_8^1h_1(\omega_4^1)\\ h(\omega_8^5)=h_0(\omega_4^1)-\omega_8^5h_1(\omega_4^1) \end{cases} \]\(h_{00}\) 代表偶数中的偶数,也就是这个数二进制下的末尾两位是不是00
\[\begin{cases} h_0(\omega_4^1)=h_{00}(\omega_2^1)+\omega_4^1h_{01}(\omega_2^1)\\ h_0(\omega_4^3)=h_{00}(\omega_2^1)-\omega_4^3h_{01}(\omega_2^1) \end{cases} \]\[\begin{cases} h_1(\omega_4^1)=h_{10}(\omega_2^1)+\omega_4^1h_{11}(\omega_2^1)\\ h_1(\omega_4^3)=h_{10}(\omega_2^1)-\omega_4^3h_{11}(\omega_2^1) \end{cases} \]继续推下去
\[\begin{cases} h_{00}(\omega_2^1)=h_{000}(\omega_1^1)+\omega_2^1h_{001}(\omega_1^1)\\ h_{00}(\omega_2^2)=h_{000}(\omega_1^1)-\omega_2^2h_{001}(\omega_1^1) \end{cases} \]\[\begin{cases} h_{01}(\omega_2^1)=h_{010}(\omega_1^1)+\omega_2^1h_{011}(\omega_1^1)\\ h_{01}(\omega_2^2)=h_{010}(\omega_1^1)-\omega_2^2h_{011}(\omega_1^1) \end{cases} \]\[\begin{cases} h_{10}(\omega_2^1)=h_{100}(\omega_1^1)+\omega_2^1h_{101}(\omega_1^1)\\ h_{10}(\omega_2^2)=h_{100}(\omega_1^1)-\omega_2^2h_{101}(\omega_1^1) \end{cases} \]\[\begin{cases} h_{11}(\omega_2^1)=h_{110}(\omega_1^1)+\omega_2^1h_{111}(\omega_1^1)\\ h_{11}(\omega_2^2)=h_{110}(\omega_1^1)-\omega_2^2h_{111}(\omega_1^1) \end{cases} \]\[h_{000}=c_0,h_{001}=c_1,...,h_{111}=8 \]这是一种递归,我讨厌递归,他很慢,所以我们考虑能不能把递归换成递推
递推部分:(这是jeefy的博客,还比较详细),我懒得写了

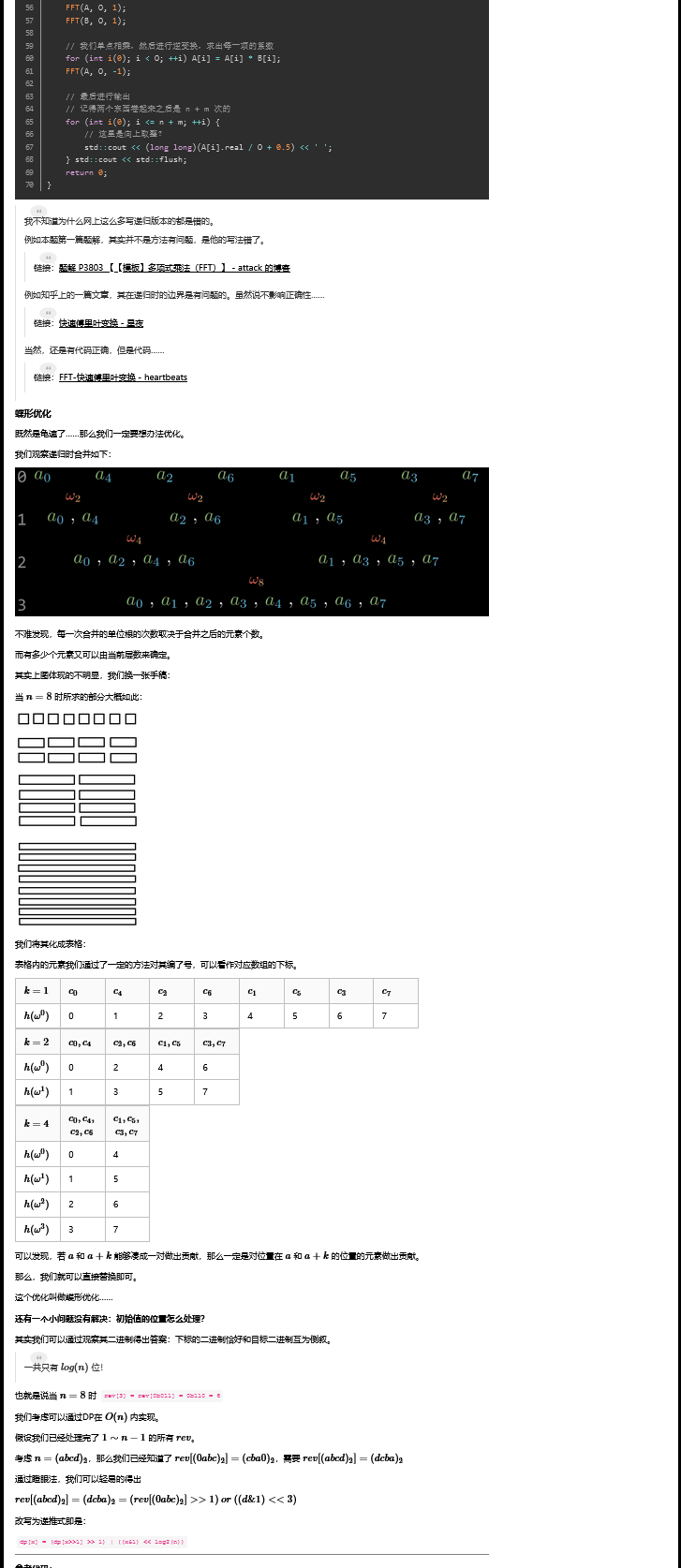
我们还有一步就是把 \(h\) 函数转回去
我们考虑这样做:
我们把 \(h\) 放入一个数列
\(<h(\omega_n^1),h(\omega_n^2),h(\omega_n^3),...,h(\omega_n^n)>\)
把这个数列在进行一次傅里叶变换,得出这个序列的离散傅里叶级数,但是是负的
\[g(\omega_n^{-k})=h(w_n^0)+h(w_n^1)\omega^{-k}+...+h(w_n^{n-1}\omega^{-(n-1)}) \]
你成功学会了FFT,当然DTT比他好十倍甚至九倍,也是一样简单
NTT
代码
FFT代码
#include<bits/stdc++.h>
#define llf double
using namespace std;
const llf PI=acos(-1);
const int N=5e6+10;
int n,m,x,rev[N],logO=0,mn;
struct Cmop{
llf x,y;
}a[N],b[N],c[N];
Cmop operator + (Cmop a ,Cmop b){return {a.x+b.x,a.y+b.y};}
Cmop operator - (Cmop a ,Cmop b){return {a.x-b.x,a.y-b.y};}
Cmop operator * (Cmop a ,Cmop b){return {a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}
void FFT(Cmop *c,int len,int op){
for(int i = 0;i < len; ++i)if(i < rev[i]) swap(c[i], c[rev[i]]);
for(int k = 1;k < len;k <<= 1){//当前有多少行
Cmop omega = {cos(PI / k),sin(PI / k * op)};
for(int j = 0; j < len;j += (k << 1)){//j列和j+1列操作
Cmop o = {1,0};
for(int i = 0; i < k; ++i){//把i行进行操作
Cmop u = c[i + j], v = o * c[i + j + k];
c[i + j] = u + v;
c[i + j + k] = u - v;
o = o * omega;
}
}
}
}
void input(){
scanf("%d%d", &n, &m);
for(int i = 0;i <= n; ++i){
scanf("%d", &x);
a[i] = {x*1.0, 0};
}
for(int i = 0;i <= m; ++i){
scanf("%d", &x);
b[i] = {x*1.0, 0};
}
}
void op(){
mn=1;
while(mn <= n+m) mn <<= 1, ++logO;
for(int i = 0;i < mn; ++i)rev[i] = (rev[i>>1] >> 1) | (( i & 1) << (logO-1));
FFT(a, mn, 1);
FFT(b, mn, 1);
for(int i = 0; i < mn; ++i){
c[i] = a[i] * b[i];
}
FFT(c, mn, -1);
for(int i = 0; i < mn; ++i){
c[i].x /= mn;
}
for(int i = 0; i <=m+n; ++i){
printf("%d ", (int)(c[i].x + 0.1));
}
}
int main(){
input();
op();
return 0;
}
NTT代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N = 4e6+10,MOD = 998244353,g = 3,revG = 332748118;
int n,m,rev[N],logO=0,mn;
ll a[N], b[N], c[N];
inline ll mpow(ll a,ll k){
ll ans = 1;
while(k){
if(k & 1) ans=(ans * a) % MOD;
a=(a * a) % MOD;
k >>= 1;
}
return ans%MOD;
}
inline void FFT(ll *c,int len,int op){
for(int i = 0;i < len; ++i)if(i < rev[i]) swap(c[i], c[rev[i]]);
for(int k = 1;k < len;k <<= 1){//当前有多少行
ll g_k = mpow(op == 1 ? g : revG , (MOD-1) / (k << 1));
for(int j = 0; j < len;j += (k << 1)){//j列和j+1列操作
ll o = 1;
for(int i = 0; i < k; ++i){//把i行进行操作
ll u = c[i + j], v = o * c[i + j + k] % MOD;
c[i + j] = (u + v) % MOD;
c[i + j + k] =(u - v + MOD) % MOD;
o = o * g_k % MOD;
}
}
}
inline void input(){
scanf("%d%d", &n, &m);
for(int i = 0;i <= n; ++i){
scanf("%lld", &a[i]);
}
for(int i = 0;i <= m; ++i){
scanf("%lld", &b[i]);
}
}
inline void op(){
mn=1;
while(mn <= n+m) mn <<= 1, ++logO;
for(int i = 0;i < mn; ++i)rev[i] = (rev[i>>1] >> 1) | (( i & 1) << (logO-1));
FFT(a, mn, 1);
FFT(b, mn, 1);
for(int i = 0; i < mn; ++i){
c[i] = a[i] * b[i] % MOD;
}
FFT(c, mn, -1);
ll inv = mpow(mn, MOD-2);
for(int i = 0; i <=m + n; ++i){
printf("%lld ", c[i]*inv%MOD);
}
}
int main(){
input();
op();
return 0;
}