模式识别
- 吴建鑫,南京大学
目录
目录- 模式识别
第一章诸论
1.模式识别流程
2.模式识别和机器学习的区别
- 大致没有什么区别,如果是传统方法,则模式识别比起机器学习更关注数据采集方面的处理,因为机器学习的输入一般是特征向量。同时机器学习需要研究模型算法的理论保证,从数学基础上给出算法可以达到的精度上限和下限。深度学习之后,大部分可能是end-to-end的学习,两者区别可能更加变小。
第二章数学背景知识
-
多变量正态分布对应单变量正态分布,其方差平方变为多变量的协方差矩阵。
-
标量对向量的求导,标量对矩阵的求导。Matrix derivation
-
最优化问题:凸函数和凸优化。推荐书籍:Convex Optimization
第三章模式识别系统的概述
- 核心部分:找到训练样本到其标记的映射:mapping
第四章评估
1.基本评价标准
- accuracy,error rate(用近似误差去估计泛化误差)
2.过拟合和欠拟合
- 过拟合指模型复杂度过低,导致模型的bias特别大。过拟合代表模型泛化能力差,可以理解为考试的时候把题库所有题目都背了,对于如果原题就效果很好,但是如果是一个新的题目就不会做。
3.训练集,测试集,验证集
-
利用验证集选择超参数,具体步骤是:1.先给出超参数集合,利用训练集训练n个分类器,然后在验证集上评估验证误差,选择合适的超参数。2.用选定的超参数在训练集上训练,使用测试集评估其性能。
-
验证集还可以用来防止神经网络的过拟合,通过早停策略(即验证误差没有减小而是开始增加时)
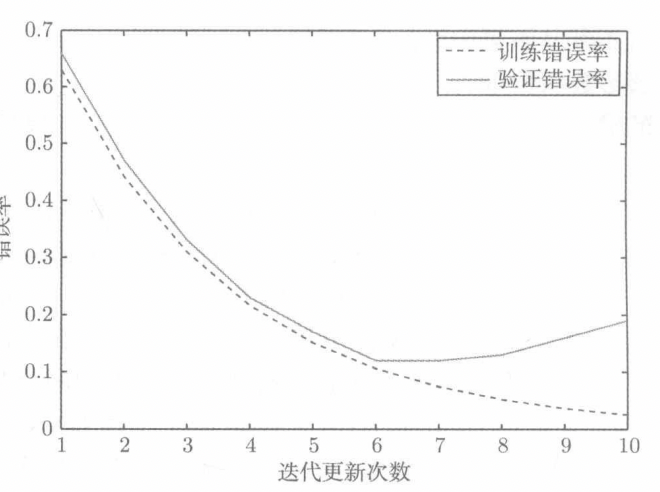
-
样本过小时,可采取交叉验证

-
最小化loss
-
损失函数替代指示函数
-
正则化,解决过拟合的问题
-
4. 不平衡问题的损失和评估
-
example:

-
所以我们需要定义合适的代价矩阵,不能就和之前一样应用简单的均方误差。ij是指真实标记y为i,且$ f \left( x \right) $预测为j所产生的损失
\[\left(\begin{matrix} { c }_{ 00 } & { c }_{ 01 } \\ { c }_{ 10 } & { c }_{ 11 } \end{matrix}\right) = \left(\begin{matrix} 0 & 10 \\1000 & 10 \end{matrix}\right) \]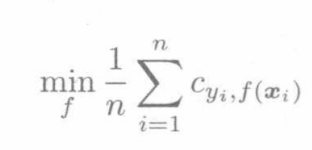
-
真实标记和预测标记的组合:TP、FN、FP、TN

-
四种率只是在单个类别上的评估结果,等价于类别上的准确率和错误率。同时还可以用另外两种查全率(recall)和查准率(precision)


-
单值评估标准:AUC-ROC和AUC-PR
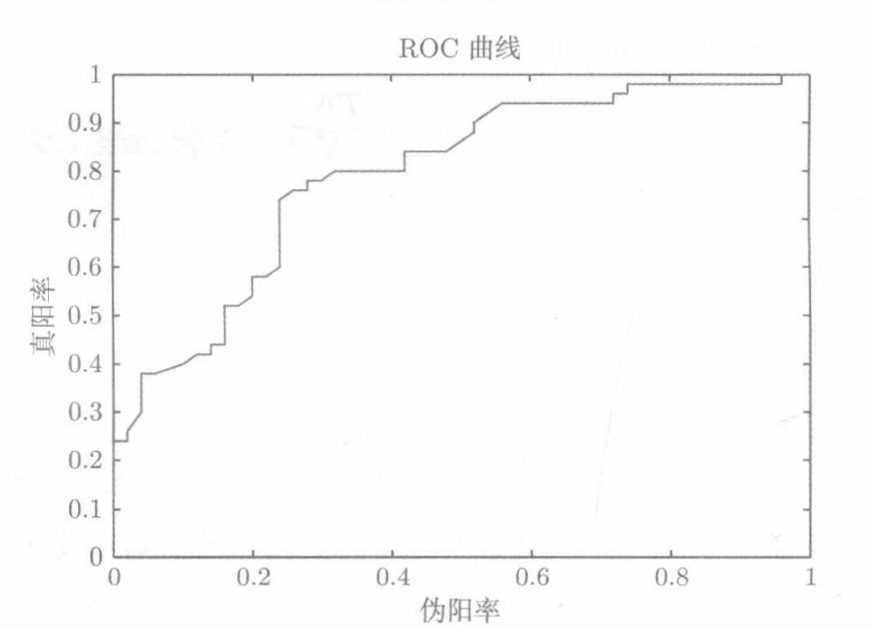
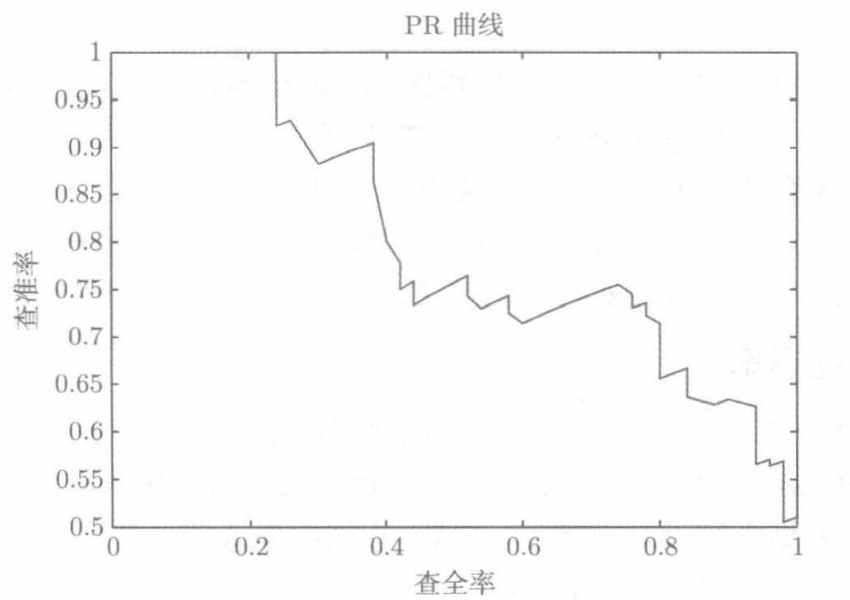
5.贝叶斯错误率,真实标记,以及偏置-方差分解
-
错误不可避免

-
贝叶斯误差
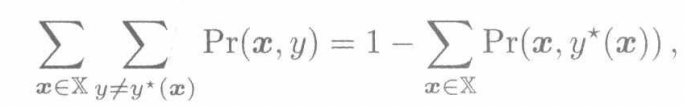
-
真实标记无法观察,都是通过人类标记产生
-
回归模型对于误差的偏置方差分解,偏置取决于模型本身的结构,方差与训练集有关。而噪声的方差不可消解
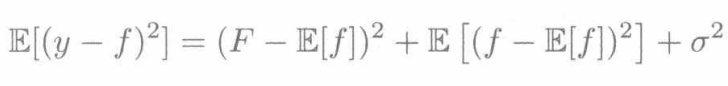
6.评估错误率的可信度,同时比较两个分类器
-
错误率取平均值,可以降低估计的方差,从而可以使得估计更为精确。而利用样本估计的标准差我们可以推断出均值的置信区间。
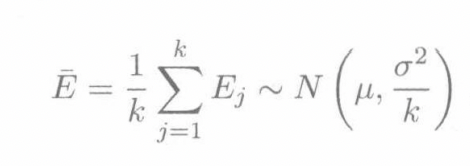

-
比较两个分类器,是通过t分布获得置信区间,原理同《概率论与数理统计》相同

第五章主成分分析:PCA
1.动机
线性降维,但是对于异常点和噪声点比较敏感
子空间方法,每多一个约束在子空间上降低一个维度
2.两个角度:最大化投影方差和最小化近似误差
-
近似角度:从零维到一维到高维,本质上是使得原向量和pca的向量之间的距离和最小,而距离pca中的用的是MSE

-
算法流程

-
主成分分析每一个维度的方差等于样本协方差矩阵的特征值
每引入一个维度都可以将平凡距离的期望减少对应的特征值。同时特征值越大,减小期望的能力越大

3.PCA和方差之间的关系
- 从最后的方差表达式中我们可以看出,对于每一个维度而言,其特征值对应的特征向量方向都是使得每一维度方差最大的方向,这一点可以通过拉格朗日乘子法进行证明,所以从近似的角度我们可以发现其与特征值的关系,同时其本质是使得每一维度方差最大化。
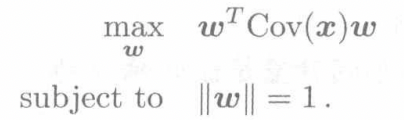
-
特征值的选择通过给定的阈值,如果已经积累的特征值超过所有特征值的d,这个选择就成立。
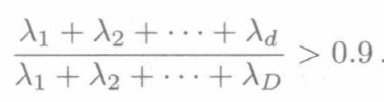
-
PCA使用效果和白化
-
对于高斯数据来说,PCA后的数据进行了一个旋转,每一个维度的变量相互独立。如果再进行一次白化,使得每一维度的数值范围相同。数据集从椭球形变成球形
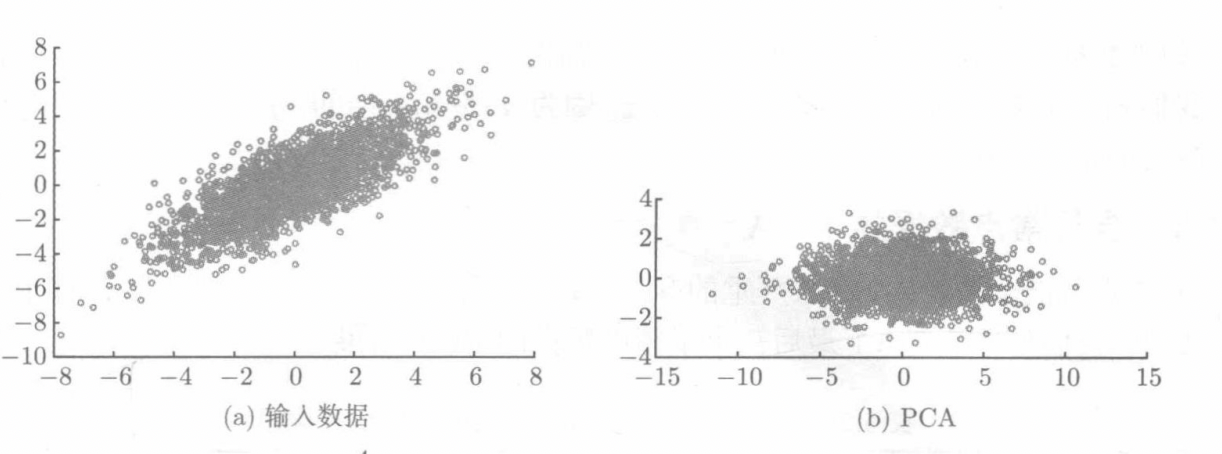
-
如果存在异常点会严重影响主成分分析的效果,导致PCA失效。
-
4.对于大型矩阵,用奇异值分解(svd)代替特征分解
-
example

第六章Fisher线性判别
1.有了PCA为什么还要引入FLD
- FLD是有监督的,可以用于分类问题的降维。而PCA是无监督的,但是很多时候这两种技术可以一起运用。
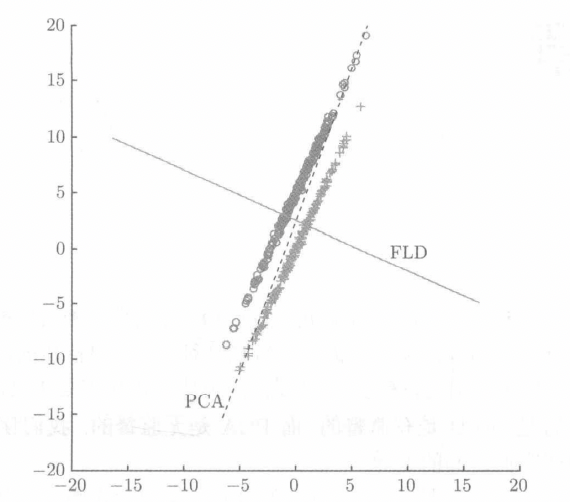
2.FLD的本质
-
FLD本质是使得正类和负类样本彼此隔得很远,即找到一个标准衡量可分性(这个标准的推导没有给详细证明,可能是一种猜想)

我们首先定义两个集合,一个是正类样本,一个是负类样本集合\(X_1=\left\{\boldsymbol{x}_i \mid 1 \leqslant i \leqslant N, y_i=1\right\}\)
同时我们定义样本的均值\(m_1 = m_1^T\omega\)、\(m_2 = m_2^T\omega\),同时还可以定义样本方差之类,最后可以推导出两个比率除法的表达式
\[\frac{|m_1-m_2|}{\sqrt{\sigma_1^2+\sigma^2_2}} \]但是论文中是用散度矩阵代替协方差矩阵,因为散度矩阵其实和协方差矩阵差不多.先定义散度矩阵\(S = \sum_{i=1}^{n}{(z_i-\bar{z})}{(z_i-\bar{z})^T}\),散度矩阵和协方差矩阵的关系是\(S_1 = N_1C_1\)。所以我们将\(m_1\)等常量用变量代入可得新的目标函数:即FLD的目标函数
\[\frac{{\omega}^T(m_1-m_2)(m_1-m_2)^T{\omega}}{{\omega}^T(S_1+S_2){\omega}} \]从本质来讲FLD是寻找一个投影方向使得类间散度大于类内距离,因此我们引入两个矩阵的定义,\(S_B\)是类间矩阵。
\[S_B = (m_1-m_2)(m_1-m_2)^T \]\[S_W = S_1+S_2 \]通过对\(\omega\)求导可得
\[S_B\omega = \frac{{\omega}^TS_B{\omega}}{{\omega}^TS_W{\omega}}S_W\omega \]所以我们可以知道我们需要找到了的投影方向是\(S_B\)和\(S_W\)的广义特征向量,根据书上推导可知。

下面给出FLD算法具体步骤

3.多分类问题的推广
-
推广到多分类问题
扩展到多分类问题,我认为找到一个投影方向使得类间散度大于类内散度这个核心思想不变,所以留给我的问题就是怎么样重新定义这两个矩阵(三个散度矩阵)。
\[S_W=\sum_{k=1}^KS_k \]\[S_T=\sum_{i=1}^N(x_i-m)(x_i-m)^T, m=\frac{1}{N}\sum_{i=1}^Nx_i \]\[S_B = \sum_{k=1}^{K}N_k(m_k-m)(m_k-m)^T, S_T =S_B+S_W \]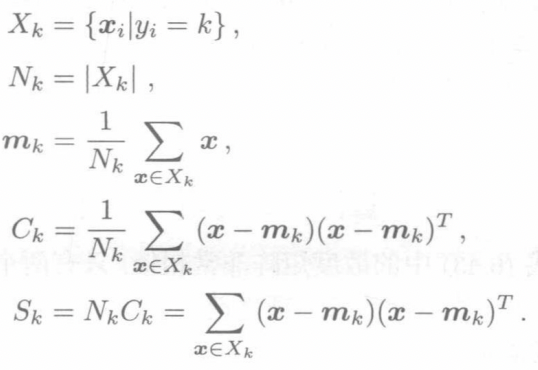
\(S_B\)这种定义有利于不平衡问题的解决,因为其具有权重,可以更关注很多数的样本。
-
总结:FLD本质上是寻找一个投影方向使得,类间散度远大于类内散度矩阵。
第七章支持向量机(svm)
1.为什么我们需要大间隔
-
大间隔的意义
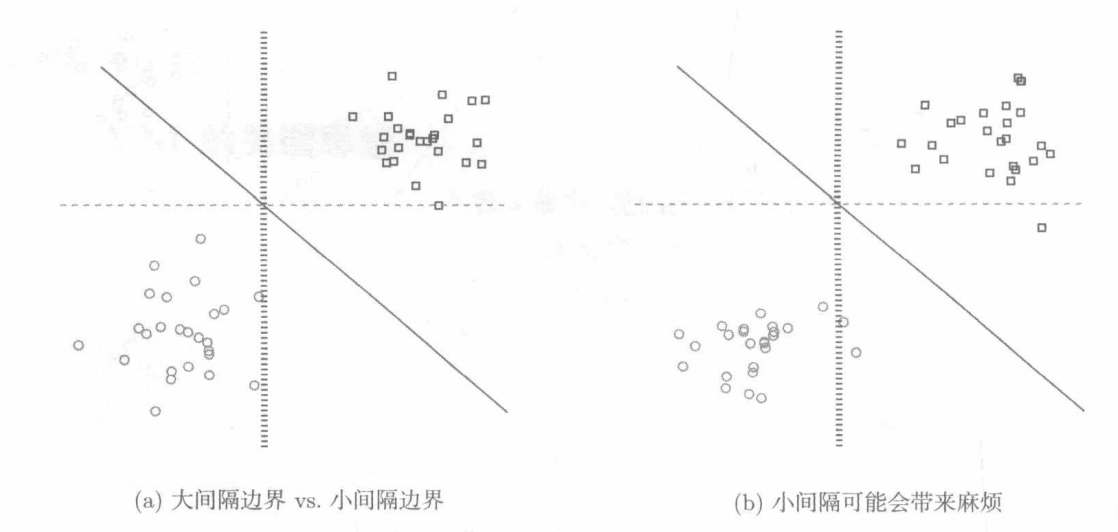
大间隔具有鲁棒性,有足够的间隔来适应扰动或者噪声的出现。
2.可视化推导svm
-
可视化距离,我们需要找到的最小间隔就是垂直距离,即法向量,在图中我们需要的距离就是\(z\),对于一个线性边界\(f(x) = {\omega}^Tx+b\)
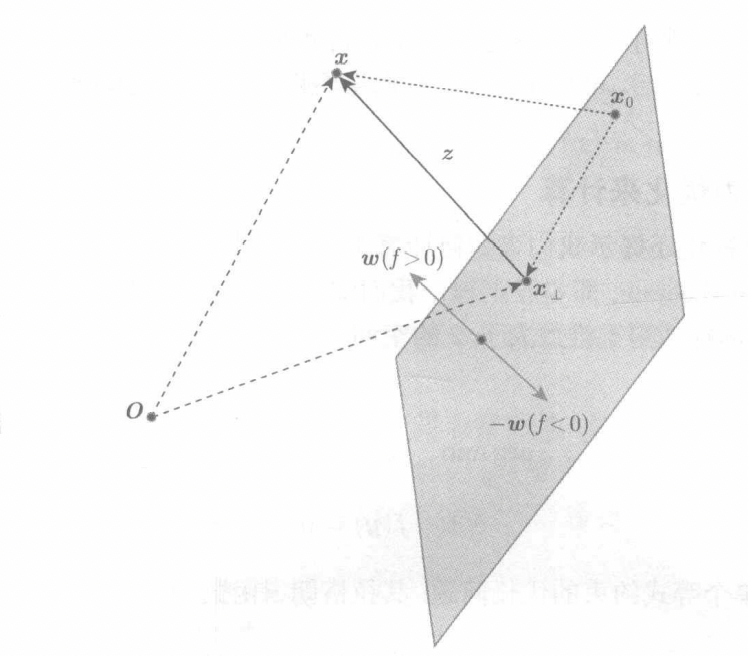
通过拉格朗日法,我们可以求得对于该线性边界,我们需要求的优化问题为
\[\max_{\omega,b}\min_{1\leq{i}\leq{n}}\frac{|f(x_i)|}{\|\omega\|} \]通过一系列化简,如固定\(\omega\)的范数为1等等,我们最后可以得到svm的最终优化表达式
\[\begin{aligned}&\min_{\omega,b}\frac12{\omega}^T{\omega}\\&s.t. y_if(x_i)\geq1, 1\leq{i}\leq{n}\end{aligned} \]
3.原始问题最终的求解答案
-
原始问题\(KKT\)条件和其对偶问题(最优化问题有讲方法)
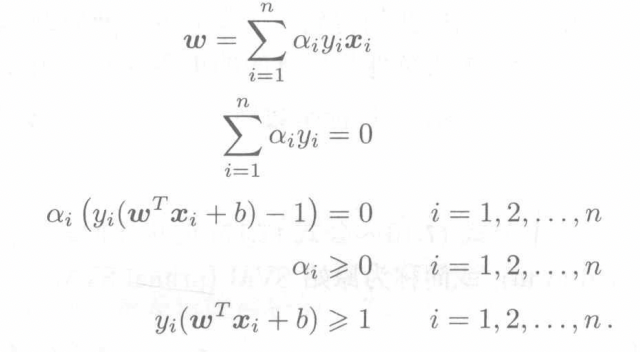
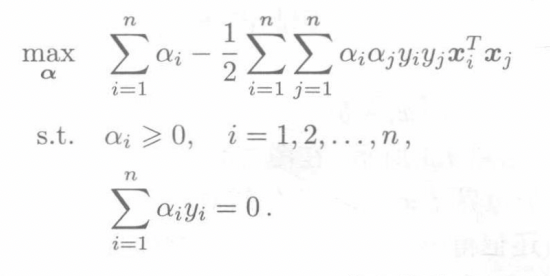
svm中对偶间隙为0,所以求原问题最小值,等于求对偶问题最大值。
-
互补松弛性质
\[\alpha_i(y_i(\omega^Tx_i+b)-1)=0 \]根据原问题的等式条件\(\omega=\sum_{i=1}^n\alpha_iy_ix_i\),当我们求得对偶问题的最大值的时候,可以直接算出投影方向向量,那对于b我们该怎么计算呢,此时就需要用到上述的互补松弛性质,根据互补松弛性质我们便可以计算b的值。对于拉格朗乘子大于0的,后一项要等于0,所以我们可以根据上述关系列出求解b的等式:
\[b = y_i-(w)^Tx_i \]所以我们找到所有非零向量的\(\alpha_i\)对应样本,求得到\(b\)的
均值。
-
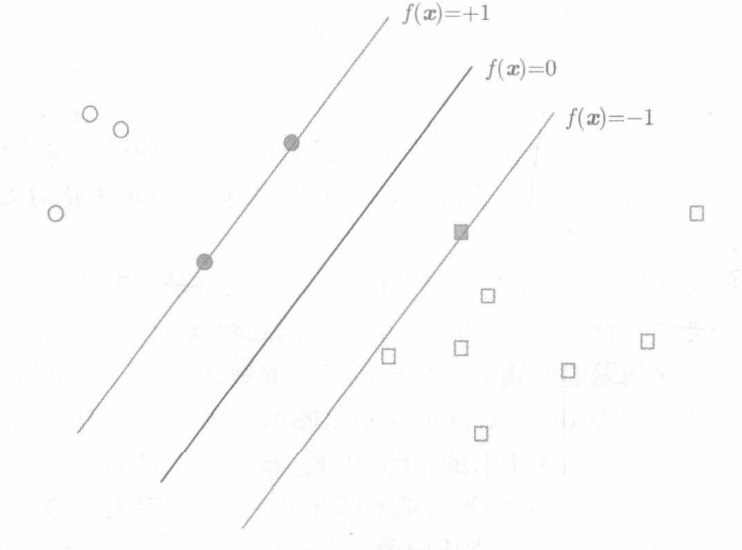
支持向量:对计算b有用的样本,所有支撑向量对于平面的间隔都是1,此时在这一点的约束被激活。
-
4.扩展到线性不可分和多类问题
-
对于大致线性可分问题,我们可以引入松弛变量技术,并不一定严格要求当前约束大于1,如果小于1就施加相应的惩罚。
\[\begin{aligned}y_if(x_i)&\geq{1-\xi_i}\\{\xi}_i&\geq0\end{aligned} \]代价函数变成
\[\min_{w,b}\frac12\omega^T\omega+C\sum_{i=1}^n\xi_i \] -
同时我们可以从另一个角度看待上述代价函数,将后一项看成损失,当间隔大于1的时候不会引起损失,而前一项是正则化项,防止线性边界过于复杂。我们可以将损失函数重写为
\[\min_{w,b}\frac12\omega^T\omega+C\sum_{i=1}^n(1-y_if(x_i))_+ \] -
扩展到多类问题,我们一个自然的想法是训练n个线性分类器,将当前样本看作正类样本,其余样本都当作负类样本。这就是OvA。而一对一方法则是训练\(\frac{m(m-1)}{2}\)个分类器,通过比较这么多张投票,那个类别票数最高来决定胜利。
5.用核函数作为相似度度量的svm
-
核svm,核方法本质上是将一个非线性分类转换为在高维特征空间一个等效线性分类问题,将对偶问题中的线性相似度度量,用非线性相似度度量代替。下为对偶问题的目标函数
\[\sum_{i=1}^n\sum_{j=1}^n\alpha_i\alpha_jy_iy_jx_i^Txj \]如果我们将内积用其他相似度度量替换可以得到一个更好的非线性分类边界,(该度量需满足Mercer条件),设度量为\(\kappa\),则在高维特征空间中,对于映射\(\phi(x)\),\(\kappa(x,y)=\phi(x)^T\phi(y)\),这个映射多数情况下无法显式的求出,被称为隐式映射。而预测过程中,由于映射无法显式的求出,所以可以通过核技巧进行预测.
\[f(x)=\sum_{i=1}^n\alpha_iy_i\kappa(x_i,x)+b \] -
常用核函数
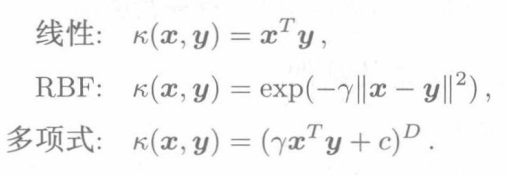
第八章概率方法
1.概率方法的本质
- 概率方法的本质就是根据已有的数据集,更新我们对于y的预测(先验概率\(p_Y(y)\)),从而得到更新后的概率,也就是后验概率\(p(Y|X)\),
2.基本知识介绍
-
贝叶斯定理,先验、后验、似然
\[p(Y|X)=\frac{p(X|Y)p(Y)}{P(X)} \]在这里\(P(X|Y)\)被称为似然,如果我们需要求后验概率有两种方法,一种是直接建模后验概率,还有一种是通过上述贝叶斯定理,先估计联合概率密度\(p(x,y)\)
-
生成式模型vs判别式模型
直接建模\(p(Y|X)\)的是判别式模型,而生成式模型代表对\(p(x,y)\)进行建模,这样可以产生新的数据,十分典型的代表就是GAN模型。
-
参数化方法(两种学派)vs非参数化方法
-
参数化方法指我们会假设特定的函数形式,并且只对这些函数中的参数进行估计,如我们可以用高斯混合模型GMM来逼近任意连续分布。
-
非参数办法指我们没有对密度函数假设一个特定的函数形式,非参数方法只是指我们没有假设参数化的函数形式,不代表这些方法不需要参数。
-
参数估计方法又分为频率学派和贝叶斯学派,频率学派核心思想是认为待估计的参数是一个固定的值,被称为点估计。而贝叶斯认为参数是一组随机向量,所以我们需要估计的不是固定的值,是一种分布。
-
3.参数化估计三种方法:ML,MAP,和贝叶斯
-
ML(maximum likelihood)

-
MAP(maximum a posteriori)
如果我们有足够的样本且似然函数是凸函数,ML十分有效。如果不满足上述条件,一种办法是利用我们已掌握的知识(先验概率)去帮助预测

-
贝叶斯估计
在贝叶斯流派中待估计的参数是一个随机变量,它的最优值是一个完整的分布

当数据比较少时,贝叶斯估计可以有效的利用先验分布的知识,但是当数据量很大时贝叶斯估计效果一般比别的方法差,同时贝叶斯估计的决策还需要通过积分来估计,因为参数是一个分布不是一个固定的值。下面展示如何通过预测的参数预测新的样本。
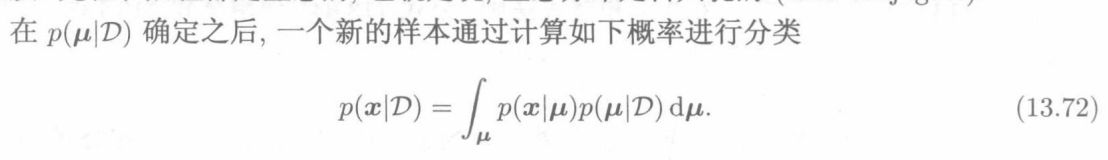
4.非参数化估计
睡觉睡觉就睡觉
-
用直方图模拟概率密度函数
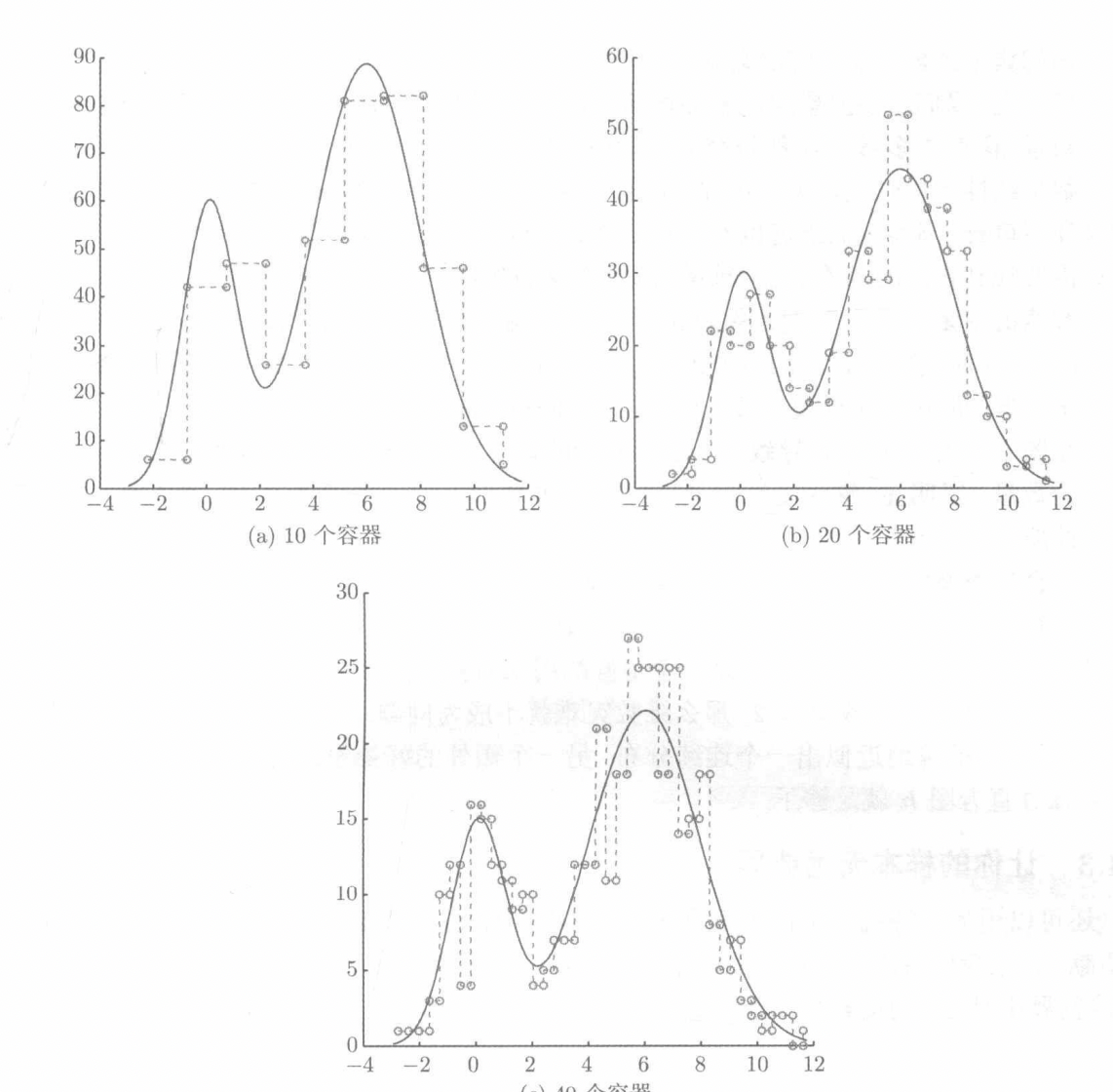
直方图存在几个问题,一个是没有连续的估计,直方图两个边界处会留下断层,其次对于很多个维度的数据,如果每个维度都需要n个容器,那么乘在一起最后会导致维数爆炸。
-
核密度估计
从样本对于容器的贡献来看,其存在非对称,支撑有限,均匀辐射的问题,所以我们引入核密度估计(KDE)解决上述问题。

参数h与直方图中的容器宽度有类似的作业,该参数被称为带宽,而带宽的选择比核函数的选择重要很多,我们已经有选择带宽的现成定理。

对于多变量,我们一般用对角GMM来逼近连续分布

第九章距离度量和数据变换
1.度量是距离的推广,同时我们经常从向量范数的中导出距离度量
-
度量定义:满足下述条件的距离函数可以称为度量
-
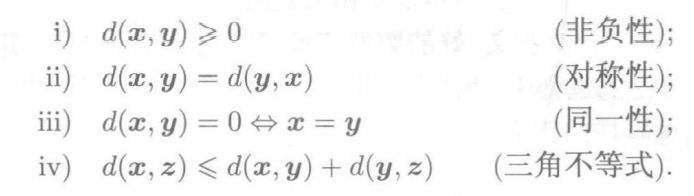
-
欧式距离和向量范数关系紧密:\(d(x,y)=\|x-y\|\),所以引入向量范数的概念,有利于我们寻找新的距离度量。下面介绍向量范数的定义
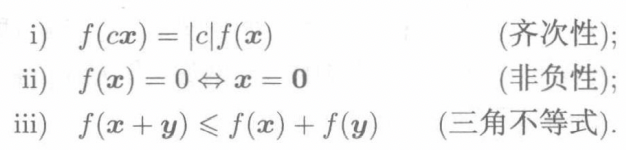
-
接下来我们引入一个重要的范数:\(l_p\)范数,\(p\geq1\)
- 当\(p=2\)显然就是我们的欧式距离,此外还有一类向量范数导出的距离马氏距离我们经常使用。

2.相似度度量:前面已经有用距离度量转化为相似度度量
-
广义平均度量
相似度 = \(\int\min(p_X(v),P_Y(v))dv\)
-
幂平均核
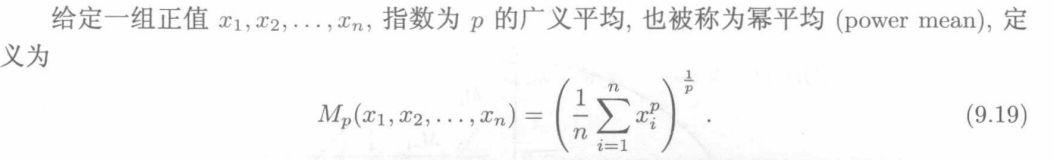
所以我们也可以用幂平均函数作为相似度的度量,定义幂平均核为
3.数据变换和规范化的引入
-
为什么要引入数据变换和规范化
因为对于不同维度的数据可能存在数值上尺度的差异,如果差异过大可能会导致模型的效果变差。
-
特征规范化
\[\hat{x_{i,j}}=\frac{x_{i,j}-x_{min,j}}{x_{max,j}-x_{min,j}} \]这样可以将第\(j\)维度数值范围规范到\((0,1)\),同时我们需要避免一个常见问题,就是用标准化训练集训练后,在测试集上我们需要用训练集上的规范化标准,因为训练集最大最小值和测试集不一样,所以规范之后两个数据不遵循一个规则。具体可见博客[特征规范化方法]((162条消息) 数据标准化常见问题:对整个数据集数据标准化后再划分训练集、测试集和先对训练级标准化再将规则用于测试集有什么区别(Python实现)_mx丶姜小辉的博客-CSDN博客),而对于高斯数据来说,我们可以利用高斯分布的方法来归一化。
\[\hat{x_{i,j}}=\frac{x_{i,j}-\mu_j}{\sigma_j} \]同时有时候我们不需要关注特征维度上尺度相同,我们需要去约束\(x\)的大小归一化,如我们输入一张图片,需要将它像素都归一化到\((0,1)\)。
-
数据变换:其实就是指用一些非线性激活函数,如sigmoid,tanh,relu,softmax等等。
-
softmax
\[z_i=\frac{exp(\gamma{x_i})}{\sum_{j=1}^{d}exp(\gamma{x_j})} \] -
tanh
\[tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} \] -
sigmoid
\[\sigma(x)=\frac1{1+e^{-x}} \]
-
第十章信息论和决策树
1.前缀码和哈夫曼编码已十分熟悉,在此略去
2.离散分布的信息论
-
离散分布的熵
熵的单位是bit,其代表的是最短可能的平均编码长度,同时也是对信息中不确定性的衡量。
\[H(X)=-\sum_{i=1}^{m}p_ilog_2p_i \]对于两个离散随机变量\(X\)和\(Y\)来说,定义其联合熵
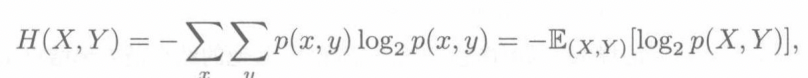
定义其条件熵
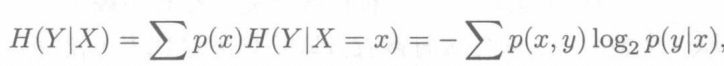
最后我们可以得出结果
\[H(X,Y)=H(X)+H(Y|X) \]条件熵可以理解为联合随机向量和随机变量\(X\)之间的信息差,顺着这个思路我们也可以定义互信息和相对熵的概念,我们定义互信息为
\[I(X;Y)=\sum_{x,y}p(x,y)log_2\frac{p(x,y)}{p(x)p(y)} \]同时可以得出互信息和熵之间的关系
\[I(X;Y)=H(X)-H(X|Y)=H(X)+H(Y)-H(X,Y) \]同时我们也经常用相对熵也就是KL散度衡量两个分布之间的差异
\[KL(p||q)=\sum_xp(x)log_2\frac{p(x)}{q(x)} \]互信息的定义可以看成其是联合分布\(p(X,Y)\)和两个边缘分布\(p(X)\)与\(p(Y)\)的信息量之差,所以我们也可以用KL散度来度量这两个分布的差,所以我们可以用KL散度来表达互信息。
\[I(X;Y)=KL(p(x,y)||p(x)p(y)) \]同时KL散度具有很多良好的性质,如我们可以利用log函数的凹凸性证明KL散度是非负的。同时我们可以用一个韦恩图总结这些性质
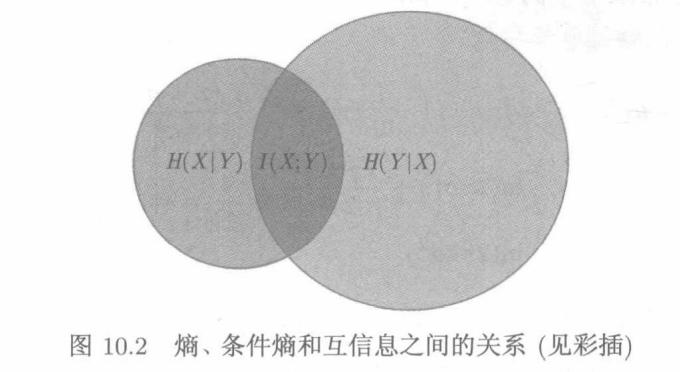
3.连续分布的信息论
-
微分熵是积分形式,其单位是nat
\[\begin{aligned}h(X)&=-\int{p(x)lnp(x)}dx\\h(X,Y)&=-\int{p(x,y)lnp(x,y)dxdy}\\h(X|Y)&=-\int{p(x,y)lnp(x|y)dxdy}\end{aligned} \]而上述对于离散熵的关系对于微分熵仍然适用,我们也仍然可以定义KL散度
\[KL(f||g)=\int{f(x)ln\frac{f(x)}{g(x)}}dx \] -
多元高斯分布的熵
\[h(X)=\frac12ln((2{\pi}e)^d|\Sigma|) \] -
高斯分布是在具有相同均值和协方差矩阵的分布中熵最大的分布。证明过程中引入了交叉熵的概念
\[ CE(p,q)=-\int{p(x)lnq(x)dx} \]同时对于任意两个概率密度函数\(p\)和\(q\),我们可以推导出
\[CE(q,p)=h(q)+KL(q||p) , CE(p,q)=h(p)+KL(p||q) \]
4.机器学习和模式识别中的信息论
-
nlp中最大熵原理经常使用,同时最大熵先验经常被使用
-
最小交叉熵
例如在softmax回归中,我们的概率函数为
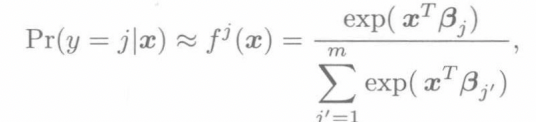
而我们目的是为了最大化\(\Pi_{i=1}^nf(x_i)^y_i(1-f(x_i))^{1-y_i}\),而如果我们对该式以二为底,则可以得到softmax的损失函数,也就是交叉熵函数。

-
特征选择
由于原始数据的维度太高,所以我们有两种办法来降低计算成本,一种是特征提取:通过降维技术从原来D维来产生d维新特征,还有一种是特征选择,从原来D维中选取一个d维的子集,特征选取目标是使得选取的特征和标签之间的互信息越大越好,而特征之间的互信息最小,而本书介绍了数据选择的一种方法:mRMR
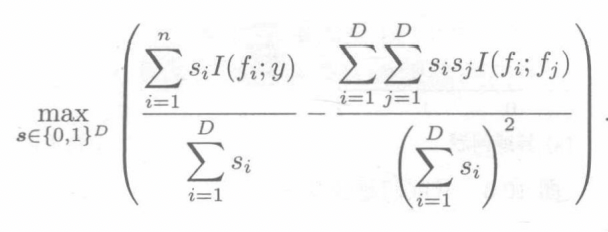
-
决策树
对于异或问题,这类线性不可分的问题,我们可以利用决策树模型来简单的解决
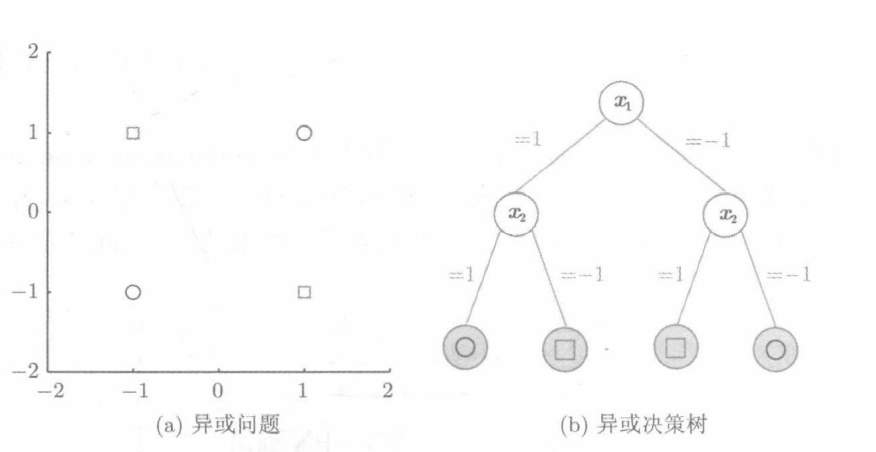
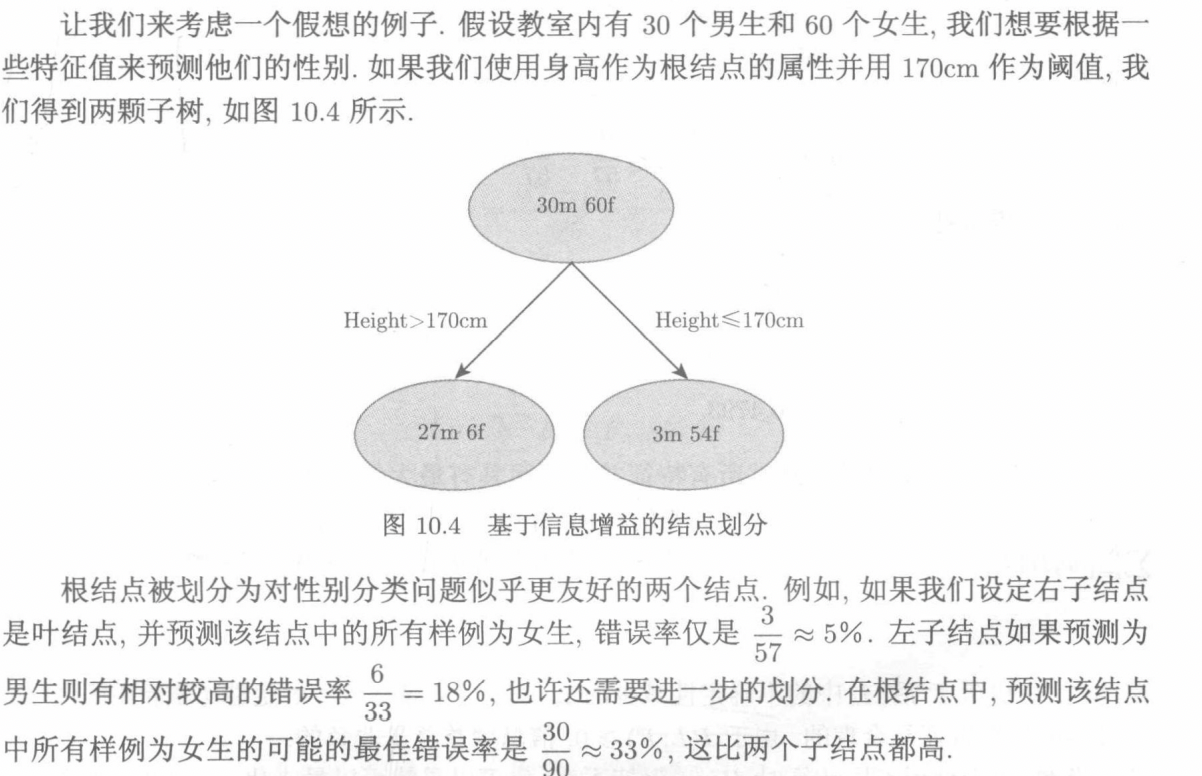
同时有了决策树之后,我们还产生了很多问题。首当其冲的就是我们该如何选择内部结点的划分标准呢,本文中介绍了一种基于信息增益的方法,在决策树中新结点的熵都比根节点小,所以信息增益就是找到一个使得熵变化最大的划分。然后我们就可以穷举所有的特征,并选择具有最大信息增益的特征,下面举出书上例子:

第十一章:稀疏数据和未对齐数据
1.稀疏机器学习
-
数据的稀疏性有助于机器学习获得良好的表示和更加出色的准确率。
-
稀疏PCA

因为\(||l_0||\)范数不连续,所以我们一般采用\(||l_1||\)范数代替,这样可以得到一个稀疏的解。而此时当我们回顾svm的解的时候:
\[\min_{\omega,b}\frac12\omega^T\omega+C\sum_{i=1}^n\xi_i \]有段这个经验损失的和可以看成原\(\xi\)向量的\(l_1\)范数,所以正则化在svm学习中也起到了作用,并且根据事实来看svm的最优解就是稀疏的,因为如果正则项不等于0,代表其是支撑向量,同时显然支撑向量也是稀疏的。
-
字典编码和稀疏编码
字典编码本质上是一种线性变换,我们可以记训练的样例为\(X=[x_1|x_2|...|x_n]\),同时将每一个向量新的表示记为\(\alpha_i\),将他们构成的矩阵记为
\[A=[\alpha_1|\alpha_2|...|\alpha_n] \]这样我们将原样本和其线性近似的误差可以记为\(X-DA\),同时我们希望对于样本的重构是稀疏的,所以我们选择优化一下目标函数:
\[min_{\alpha_i}||x_i-D\alpha_i||+\lambda||\alpha_i||_1 \]D被称作字典,我们其实是用字典的加权组合来逼近样例,这不经让我想到鲁鹏老师的词袋任务,就是先用特征提取构成一个词典,再通过词典进行特征提取。
eg:

2.动态时间调整
-
本章研究的是对齐的问题,在人脸识别中,我们想计算两张人脸之间的相似性或者距离,都需要是对齐的正面人脸,而本章我们主要研究时序数据的对齐,如拼写错误的单词对齐,本文主要介绍了一种动态对齐算法DTW

DTW的三条规则

但是由于第二条存在某些问题,所以我们更新规则为
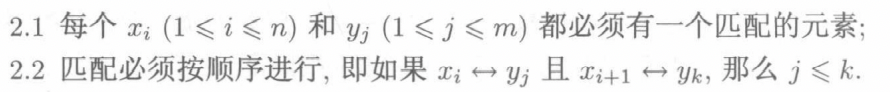
杜绝交叉的情况有利于我们利用动态规划的思想进行优化,在这些规则下,我们可以将两个序列之间的匹配转化为曼哈顿街区的一条路径。
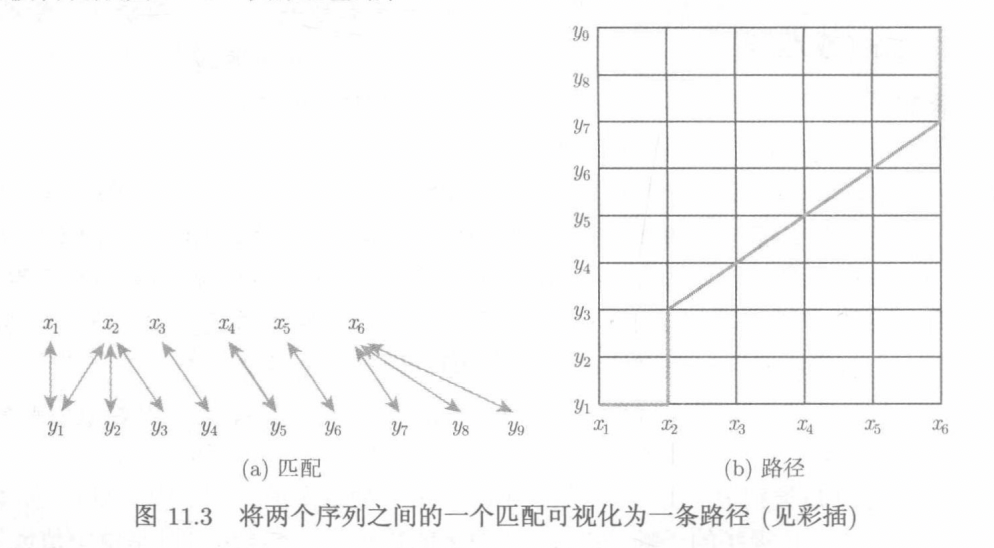
所以我们每一次的选择只有向右、向上或者向右上,此时我们便找到了每次行走的递推关系了。
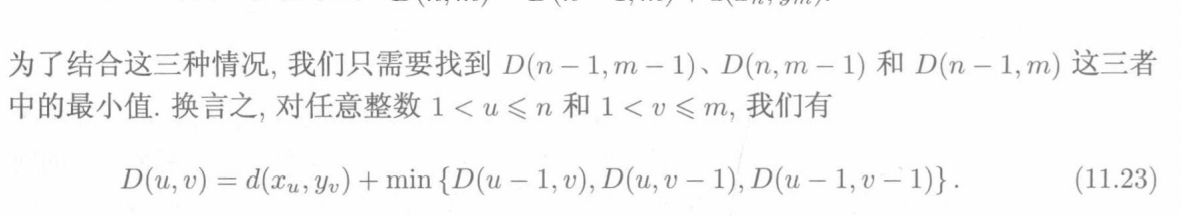
此时我们便可以编写动态规划程序求解,递归程序的编写十分简单,采用记忆化dfs就可以完美解决这个问题的。
第十二章隐马尔可夫模型
第十三章正态分布基础概念
1.单变量正态分布定义
\[p(x)=\frac1{\sqrt{2\pi\sigma}}{e^{-\frac{(x-\mu)^2}{2\sigma^2}}} \]2.多变量正态分布定义和性质
\[p(x)=\frac1{(2\pi)^{\frac{d}2}|\Sigma|^\frac12}exp(-\frac12(x-\mu)^T(x-\mu)) \]- 也可以记为
-
上述方法为矩参数参数方法,同时我们还有正则参数化形式

-
正态分布具有线性运算性质

3.条件分布的概率密度,高斯分布乘积
-
条件分布的概率密度

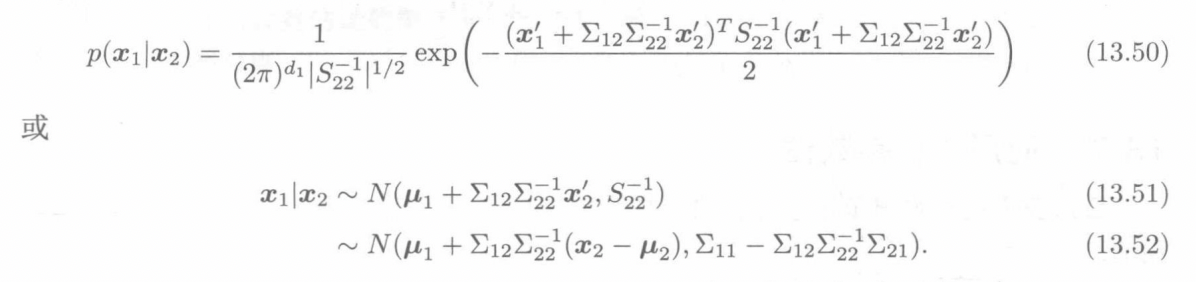
-
高斯分布的乘积还是高斯,有助于解决之前第八章的问题

4.应用:参数估计和卡尔曼滤波
-
最大似然估计中的应用

-
贝叶斯参数估计

-
卡尔曼滤波笔者不太知道这个相关知识所以没太看懂
第十四章EM算法基本思想
1.EM算法的本质
- EM算法的本质思想是第一步我们利用后验概率分布去近似原本变量\(Z\)的概率分布,同时第二步我们最大化完整数据对数似然对后验分布的期望
2.从GMM高斯混合模型出发引入基本概念
-
高斯混合模型的基本概念

-
从隐变量出发理解高斯混合模型,我们可以认为存在一个上帝,在提供数据的时候,他是先选择这几个高斯分布中的一个。然后我们看到是这个数据,但是问题来了,我们可能观测到这个z的概率吗,答案是否定的。

那我们可以通过观察到的数据集猜测其对应的隐变量吗,根据我们的信息,逐渐迭代产生的后验概率作为替代z分布的概率分布是最为合适的,而EM算法就是通过逐次迭代逼近真实的分布,最后我们利用后验概率求期望值便可以得到最可能的分布。
3.核心思想解释
-

-
而估计参数\(\theta\)我们用的是最大似然估计,同时我们还分不完整数据对数似然,这个是只考虑变量X的对数似然。而完整对数似然则考虑了X和Z
完整数据对数似然是凹函数,具有良好的性质,方便我们优化求解
4.EM推导:是利用KL散度逼近真实的隐变量分布
-
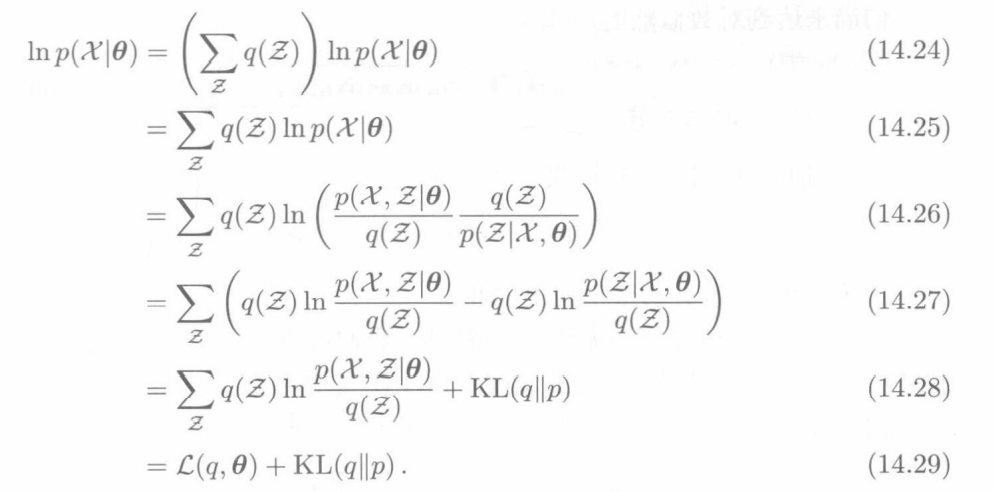
然后我们知道KL散度是大于0的,所以我们知道前面目标函数的下界是\(L(q,\theta)\),首先这个等号成立代表我们已经用后验概率代替了原始的概率分布, 然后我们可以通过优化这个函数来优化原始的目标函数。

接下来我们用后验概率代替原始分布\(q(z)\),可以推导出\(L\)函数新的形式,也就是EM算法中需要优化的期望:

所以在这里我们就可以总结出EM算法的具体流程:
1.求出并且更新后验概率
2.求出完整对数似然对后验分布的期望
3.同时最大化这个期望的同时,我们可以得到参数最优化形式
4.EM算法的具体流程
5.在GMM模型上实际应用EM算法
-
首先我们要求后验概率,而现在,根据上一轮已经更新完的参数,我们已经可以更新概率分布:\(p(x_j|\theta^{(t)})\)\(p(x_j,z_{ij}|\theta^{(t)})\),我们可以将他们的概率表示出来,展示在下方:
\[p(x_j|\theta^{(t)})=\sum^N_{i=1}\frac{\alpha_j}{(2\pi)^{\frac{d}2}|\Sigma_j|^\frac12}exp(-\frac12(x-\mu)^T\Sigma^{-1}_j(x-\mu)) \]而\(p(x_j,z_{ij}|\theta^{(t)})\)可以显示的表达为(当\(z_{ij}\)为真时),否则概率直接等于0
\[p(x_j,z_{ij}|\theta^{(t)})=\frac{\alpha_i}{(2\pi)^{\frac{d}2}|\Sigma_i|^\frac12}exp(-\frac12(x-\mu)^T\Sigma^{-1}_i(x-\mu)) \]从而根据上述两个式以及贝叶斯公式,我们可以推导出后验概率
\[p(z_{ij}|x_j,\theta^{(t)})=\frac{p(x_j,z_{ij}|\theta^{(t)})}{p(x_j|\theta^{(t)})} \]得到后验概率后,我们已经完成了EM算法中的E步,下一步是最大化期望
-
最大化期望
期望表达式
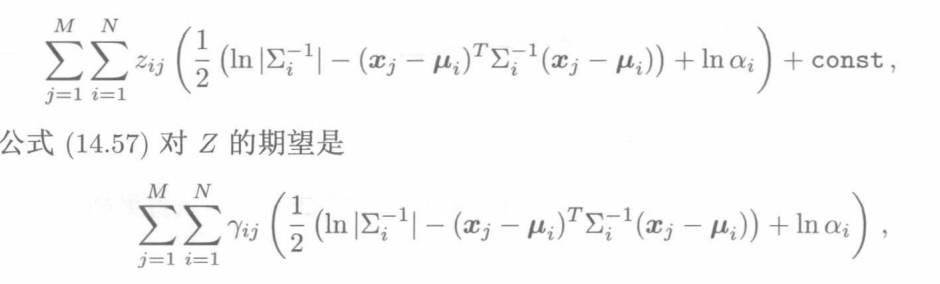
此时$ \gamma_{ij}\(就是对于后验概率求期望,\) \gamma_{ij}=p(z_{ij}=1|x_j,\theta{(t)})$,而等式右边可以用上述贝叶斯公式求解,对于$p(x_j,z_{ij}|\theta)\(来说\)p(x_j,z_{ij}=1|\theta{(t)})=p(z_{ij}=1|\theta)p(x_j|z_{ij}=1,\theta{(t)})$,而$p(z_{ij}=1|\theta)=\alpha_i{(t)}$,同时对于$p(x_j|z_{ij}=1,\theta) = N(x_j;\mu_{i}{(t)},\Sigma)$,所以我们可以求得这个期望的大小。计算出来这个期望表达式,之后我们要最大化这个完整数据似然,显然其为凸函数,所以我们可以用拉格朗日数乘法来优化,进行推导之后我们可以得到GMM的完整更新规则