素数与整除
1.费马小定理
2.威尔逊定理\((p-1)!\equiv -1(mod\ p)\)
2.欧拉函数,欧拉定理,欧拉函数的计算方式,欧拉定理的推论,欧拉函数的推论
3.\(gcd\)和\(lcm\)的转化
4.筛法:埃氏筛,欧拉筛,暴力筛
5.\(gcd\) 辗转相除法(欧几里得算法),更相减损法(二进制优化)
6.裴蜀定理和\(exgcd\)的应用及证明
int exgcd(int a, int b){
if(b == 0){
x = 1; y = 0;
return a;
}
int tmp = exgcd(b, a%b);
z = x, x = y, y = z - a / b * y;
return tmp;
}//ax+by = gcd(a, b);
同余
7.同余的基本性质
8.逆元
<1> 求解 \(ax \equiv 1 (mod\ b)\) 即 \(ax + by = 1\);
<2> 费马小定理,快速幂求\(a^{p-2} \equiv 1(mod\ p)\)
<3> 线性求逆元 \(inv_i = (p - \lfloor \frac{p}{i} \rfloor *inv_{p \ mod\ i})\ mod \ p\)
9.PS:插播一条恶心gcd
求解 \(ax+by=gcd(a,b) = d\) 得到 \(x_0, y_0\) 两个解
继续同乘 \(\frac{c}{d}\) 得到\(\frac{acx_0}{d} +\frac{bcy_0}{d} = c\)
所以 \(ax+by = c\) 的解就是 \(x_1 = \frac{x_0c}{d}, y_1 = \frac{y_0c}{d}\)
所以构造通解 \(a(x_1+kb)+b(y_1-ka)=c\) 其中 \(ka\) 和 \(kb\) 为整数
当 \(k\) 取道最小值的时候能保证相邻两个解之间相差 \(kb\)、\(k a\)
所以 \(d_x=kb=\frac{b}{d},d_y=ka=\frac{a}{d},k=\frac{1}{d}\)
那么通解就是
\[\begin{cases} x = x_1 + sd_x\\ y = y_1 - s d_y\\ \end{cases} \] 如果要是有正整数解的话就是
\[\frac{-x_1}{d_x} < s <\frac{y_1}{d_x} \] 转化一下
\[\lceil\frac{-x_1+1}{d_x}\rceil \leq s \leq \lfloor\frac{y_1-1}{d_y} \rfloor \]- 中国剩余定理(CRT)
求解线性同余方程组
- \(EXCRT\)(模数不互质)
取其中两个同余方程
\[\left\{\begin{matrix} x \equiv a_1(mod\ m_1)\\ x \equiv a_2(mod\ m_2) \end{matrix}\right. \]转化一下
\[\left\{\begin{matrix} x = a_1 + k_1m_1\\ x = a_2 + k_2m_2 \end{matrix}\right. \]联立
\[a_1+k_1m_1 = a_2 + k_2m_2 \]化简
\[k_1m_1 +(-k_2)m_2 = a_2 - a_1 \]是一个形如\(ax + by = c\)的二元一次不定方程,用\(exgcd\)求解,注意这里存在无解的情况。
之后求得通解
\[k_1 = k_1'+ n\frac{m_2}{gcd(m_1,m_2)} \]代回原式
\[x = a_1 + k_1'm_1 + n\frac{m_1m_2}{gcd(m_1,m_2)} \]转化
\[x \equiv a_1 + k_1'm_1(mod\ lcm(m_1, m_2)) \]由此我们又构造了一个形如\(x \equiv a(mod\ m)\)的同余方程,方程数量-1,以此类推,最后会得到这样一个柿子
\[x \equiv ?(mod\ lcm(m_1,m_1......m_n)) \]就解决辣
Lucas定理(p为质数)
\[C^m_n\ mod\ p = C^{\lfloor m/p\rfloor}_{\lfloor n/p\rfloor}C^{m\ mod\ p}_{n\ mod\ p}\ mod\ p \]exLucas定理
数论函数
1.欧拉函数
2.莫比乌斯函数
性质:
\[ \sum_{d|n} \mu(d) = e(n) = [n = 1] = \sum_{j|n}^k\binom{k}{j} *(-1)^j \]3.数论函数们
4.狄利克雷卷积
\[h(n) = \sum_{d|n} f(d)g(\frac{n}{d})\\ h = f * g \]ps: *记号代表卷积
\[\sum_{d|n} \mu(d)id_0(\frac{n}{d}) = [n = 1] \]so
\[\mu *id_0 = e \]so
\[\sum_{d|n} f(\frac{n}{d})e(d) = f(n) \]5.卷积拓展
First
\[\phi*id_0 = id_1 \]即
\[\sum_{d|n} \phi(d) = n\\ \sum_{d|n}\sum_{i=1}^{d}[gcd(i, d) = 1]\\ \sum_{d|n}\sum_{i=1}^{d}[gcd(i*\frac{n}{d}, n) = \frac{n}{d}] \]组合计数
1、n个球,m个盒子(111 ->相同球,相同盒,可空)
101 : \(\binom{n-1}{m-1}\)
鸽巢原理
100 : \(\binom{n+m-1}{m-1}\)
001 : \(m^n\)
010 :
考虑dp
\[状态:f_{i,j} 表示已经把i个小球分进j个盒子\\ 转移:f_{i,j} = f[i-1][j-1] + f[i-1][j] * j;\\ \]通俗解释:
考虑第i个球,可以放进一个新的盒子,方案数为\(f[i-1][j-1]\)
也可以放进原来的盒子里,因为球各不相同,所以放进每个盒子的方案不同,所以这种情况的方案数就是\(f[i-1][j] * j\)
ps:第二类斯特林数:n个不同的小球放进m个相同的盒子的方案数即
\(f_{n,m}\)。
计算式:
011 : 同上,因为有空盒,所以答案是
\[\sum_{i=1}^{m} f_{n,i} \]解释:每次有 \(i\) 个盒子放球,\(m-i\) 个空盒
2、容斥原理
- 公式化表达(韦恩图理解一下
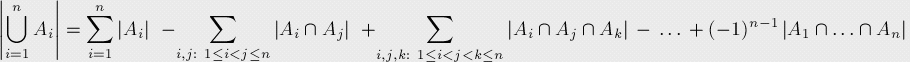
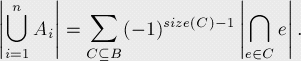
-
二项式定理
\[(a+b)^k = \sum_{i=0}^nC_n^ia^{n-i}b^i \] -
二项式反演
线性代数
矩阵
1.基本性质,矩乘快速幂,加速递推
2.逆矩阵
\[AA^{-1} = \ \]\(A^{-1}\)即为A的逆矩阵,求逆感性理解。
两个矩阵(A和单位矩阵),其中A矩阵化成单位矩阵(高斯消元)时,另一个就是逆矩阵
3.矩阵树定理
标签:frac,gcd,sum,数学,混讲,equiv,定理,mod From: https://www.cnblogs.com/Lkkaknoi/p/17076704.html