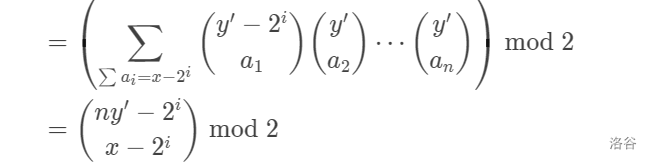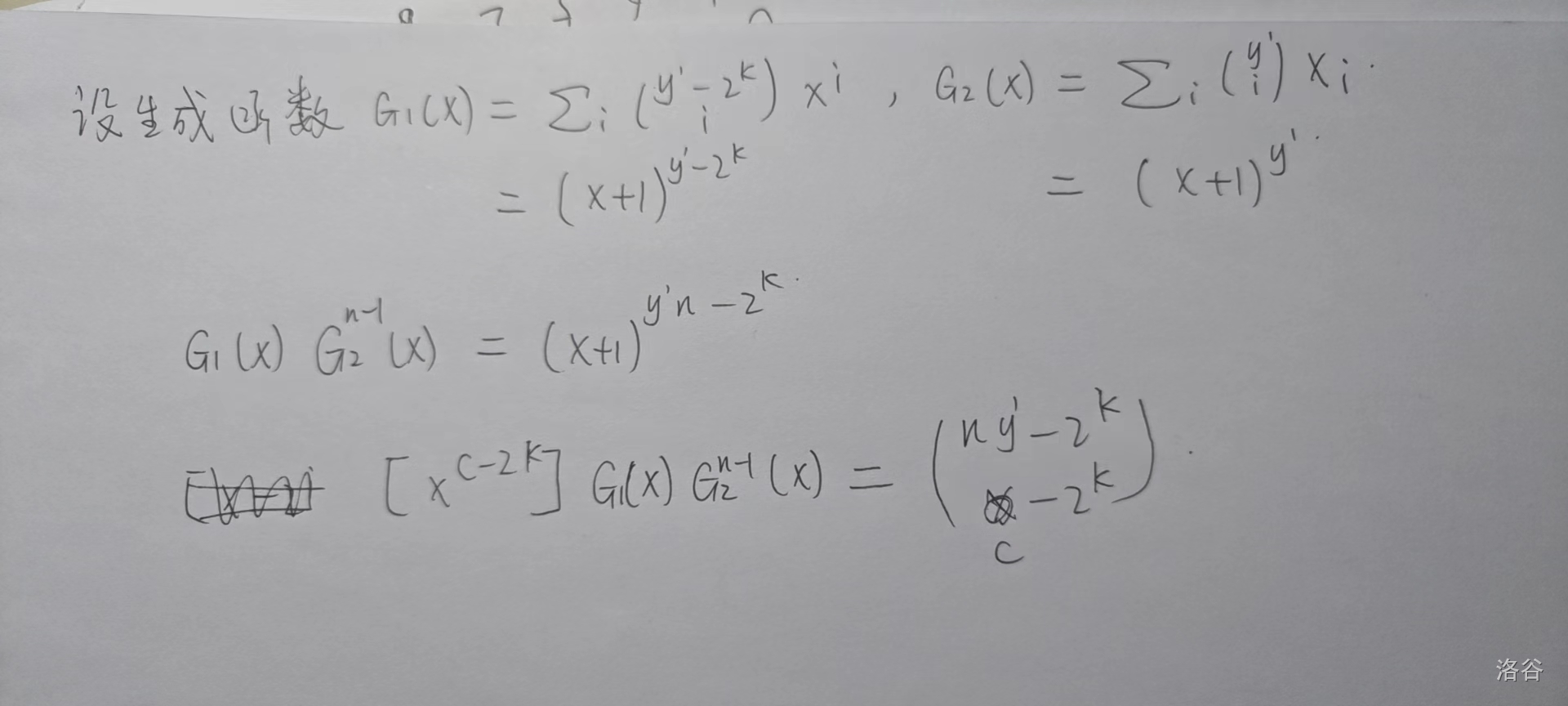上接 https://www.cnblogs.com/juruo-zzt/p/15369446.html
可能循环论证了!
范德蒙德卷积
\[\sum_i\binom ni\binom m{m-i}=\binom{n+m}{n} \]\[[x^n](x+1)^{n}(x+1)^m=[x^n](x+1)^{n+m}=\binom{n+m}{n} \]上指标求和
\[\sum_{i=0}^a \binom{i}{b}=\binom{a+1}{b+1} \]\[[x^a]\frac{1}{1-x}\cdot \frac{x^b}{(1-x)^{b+1}}=[x^a]\frac{x^b}{(1-x)^{b+2}}=\binom{a+1}{b+1} \]不知道叫什么的神秘公式
\[\sum_{i=a}^{n-b} \binom{i}{a}\binom{n-i}{b}=\binom{n+1}{a+b+1} \]\[[x^{a+b}]\frac{x^a}{(1-x)^{a+1}}\cdot\frac{x^b}{(1-x)^{b+1}}=[x^{a+b}]\frac{x^{a+b}}{(1-x)^{a+b+2}}=\binom{n+1}{a+b+1} \]神秘公式 2