首先我不太清楚什么是解析几何什么是计算几何,总之在这里它指在平面内的一些计算。
向量
定义
为了写程序方便,引入向量 \(\vec{a}=(x,y)\)。\(\vec{a}\) 本质上是一个点的偏移量,因此我们不关心它的起点是什么,可以减,例如两个点 \(A=(x_1,y_1),B=(x_2,y_2)\),有向线段可以表示为向量 \(\vec{AB}=(x_2-x_1,y_2-y_1)\)。注意到令 \(O=(0,0)\) 为原点,\(\vec{OA}=(x,y)=A\) 因此向量可以用点的方式存储。
令 \(\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)\),定义一些运算:
- 向量模长:\(|\vec{a}|=\sqrt{x^2+y^2}\).
- 向量加法:\(\vec{a}+\vec{b}=(x_1+x_2,y_1+y_2)\)。
- 向量减法:\(\vec{a}-\vec{b}=(x_1-x_2,y_1-y_2)\)。
- 向量数乘:\(\lambda\vec{a}=(\lambda x,\lambda y)\)。
- 向量点乘:\(\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2\)。
- 向量叉乘:\(\vec{a}\times\vec{b}=x_1y_2-x_2y_1\)。
叉积
重点看叉积,我们声明其符号为 \(\times\)。点乘就叫做 \(\cdot\) 好了:
看一张图:
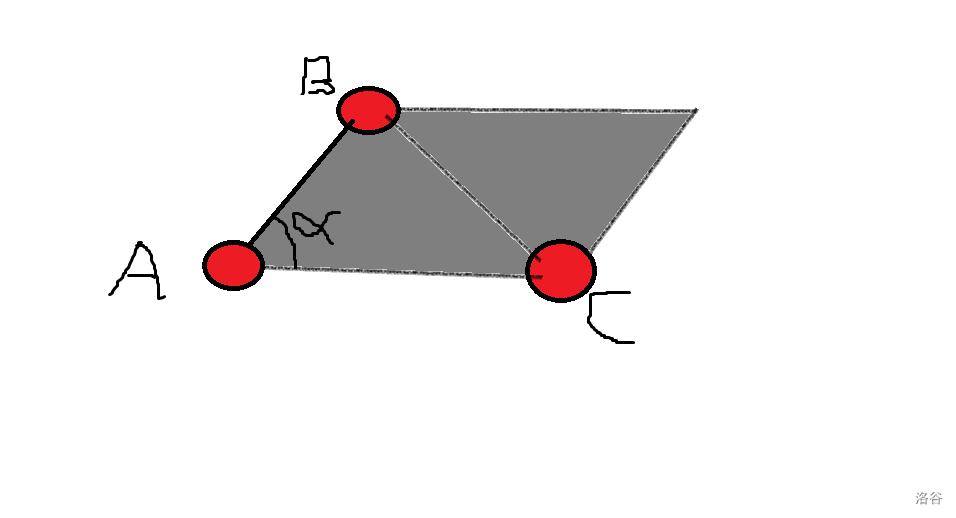
如图,当 \(\alpha\leq180^\circ\) 时,\(\vec{AC}\times\vec{AB}\geq 0\),也就是这个灰色的平行四边形的面积,或者说是:
- \(\vec{AC}\) 绕点 \(A\) 逆时针旋转到 \(\vec{AB}\) 所扫过的平行四边形的面积。
如果反过来 \(\vec{AB}\times\vec{AC}\leq 0\) 就是 \(\vec{AB}\) 反过来(顺时针)转到 \(\vec{AC}\) 扫过的平行四边形面积的相反数。
- \(\vec a\times\vec b=X_aY_b-X_bY_a\)。(据说是可以推的,但是我不会)
- 两个起点不同的向量要叉乘,可以将其中一个向量平移,使两个向量起点相同就可以叉乘。
- \(\vec a\times \vec b=-\vec b\times\vec c\)。没有交换律。
向量运算的性质定理
以下是一些小性质,或者叫定义,我不知道:
- \(\vec a\times\vec b=X_aY_b-X_bY_a\)。
- 平行判定:\(a//b\Leftrightarrow\vec a\times \vec b=0\)。
- 垂直判定:\(a\perp b\Leftrightarrow\vec a\cdot \vec b=0\)。
- 模长:\(|a|=\sqrt{x^2+y^2}=\sqrt{a\cdot b}\)。
- 辐角:\(\theta=\arctan \frac{y}{x}\)。
这里提供一个 OI 板子:
template<class T=double> struct dot{
T x,y;
dot(T x=0,T y=0):x(x),y(y){}
dot operator+(dot b){return dot(x+b.x,y+b.y);}//向量加
dot operator-(dot b){return dot(x-b.x,y-b.y);}//向量减
dot operator*(T k){return dot(x*k,y*k);}//数乘,或叫放缩
T operator*(dot b){return x*b.y-b.x*y;}//叉乘
T operator^(dot b){return x*b.x+y*b.y;}//点乘,对应坐标相乘
friend T dist(dot a){return sqrt(a^a);}//绝对值 / 模长,即到原点的距离
};
当然我们这是数学不是 OI,所以以下我们暂时不管过程啊。要写过程就怎么呢,过点 A 作 \(x\) 轴、\(y\) 轴的垂线,云云,不管。
三角形的面积
\(\Delta ABC\),则 \(S=|\frac{1}{2}\vec{AB}\vec{AC}|\)。
平行四边形:
平行四边形 \(ABCD\)(已经有顺序了),判定的原则是:\(\vec{AD}=\vec{BC}\),或者反过来,就是平行且相等。如果一组对边平行,另一组对边相等,我们 HL 移一下可以知道是一样的。
这里我们思考一个问题:已知点 \(A,B,C\),求剩下一个点 \(D\) 使它们组成平行四边形的方案数。一共六种,\(3\) 个重根,剩下的分别是:
- \(A+\vec{BC}\)
- \(B+\vec{CA}\)
- \(C+\vec{AB}\)
等腰直角三角形
等腰 \(Rt\Delta ABC\),其中 \(\angel B=90^\circ\),它的判定是什么?
- \(|\vec{AB}|=|\vec{BC}|\)
- \(AB\prep BC\)
我们仔细思考一下会发现:其实是 \(\vec{BA}\) 和 \(\vec{BC}\),关于 \(x\) 轴或 \(y\) 轴对称。
标签:AB,return,八上,times,解析几何,vec,dot,向量,薄纱 From: https://www.cnblogs.com/caijianhong/p/16999127.html