标签：angle Kalman 卡尔曼滤波 float slam14 ardunio print Serial dt

代码

https://github.com/TKJElectronics/KalmanFilter

原理剖析

原理2 卡尔曼融合滤波

https://zhuanlan.zhihu.com/p/36374943

关键点

1 他的偏置和噪声方程根据经验给了数值

经过验证，初始参数设置为以下值时适用于大多数的IMU，并且这些初始参数将会使mpu6050工作在最佳状态；

float Q_angle = 0.001;
float Q_gyroBias = 0.003;
float R_measure = 0.03;

2 误差的计算测量值-预测值

状态转移矩阵是1

测量值z 使用x和y相对于z轴重力的arctan计算的

#ifdef RESTRICT_PITCH // Eq. 25 and 26
  double roll  = atan2(accY, accZ) * RAD_TO_DEG;
  double pitch = atan(-accX / sqrt(accY * accY + accZ * accZ)) * RAD_TO_DEG;
#else // Eq. 28 and 29
  double roll  = atan(accY / sqrt(accX * accX + accZ * accZ)) * RAD_TO_DEG;
  double pitch = atan2(-accX, accZ) * RAD_TO_DEG;
#endif

　进一步算残差

kalAngleX = kalmanX.getAngle(roll, gyroXrate, dt);

原理1 IMU本身运行和坐标系转换积分原理

IMU姿态解算

IMU，即惯性测量单元，一般包含三轴陀螺仪与三轴加速度计。之前的文章

https://zhuanlan.zhihu.com/p/165156300

MPU6050基本功能

3轴陀螺仪

陀螺仪，测量的是绕xyz轴转动的角速度，对角速度积分可以得到角度。

3轴加速度计

加速度计，测量的是xyz方向受到的加速度。在静止时，测量到的是重力加速度，因此当物体倾斜时，根据重力的分力可以粗略的计算角度。在运动时，除了重力加速度，还叠加了由于运动产生的加速度。

DMP简介

DMP就是MPU6050内部的运动引擎，全称Digital Motion Processor，直接输出四元数，可以减轻外围微处理器的工作负担且避免了繁琐的滤波和数据融合。Motion Driver是Invensense针对其运动传感器的软件包，并非全部开源，核心的算法部分是针对ARM处理器和MSP430处理器编译成了静态链接库，适用于MPU6050、MPU6500、MPU9150、MPU9250等传感器。

四元数转欧拉角

四元数可以方便的表示3维空间的旋转，但其概念不太好理解，可以先类比复数，复数表示的其实是2维平面中的旋转。

四元数的基本表示形式为：q0+q1*i+q2*j+q3*k，即1个实部3个虚部，具体细节本篇先不做展开介绍。

四元数虽然方便表示旋转，但其形式不太直观，旋转转换成pitch、roll、yaw的表示形式，方便观察姿态。

四元数的基本表示形式为：q0+q1*i+q2*j+q3*k，即1个实部3个虚部，具体细节本篇先不做展开介绍。

四元数虽然方便表示旋转，但其形式不太直观，旋转转换成pitch、roll、yaw的表示形式，方便观察姿态。

转换公式为：

https://zhuanlan.zhihu.com/p/195683958

本篇的姿态解算选用的旋转顺序为ZYX，即IMU坐标系初始时刻与大地坐标系重合，然后依次绕自己的Z、Y、X轴进行旋转，这里先自定义一下每次的旋转名称和符号：

绕IMU的Z轴旋转：航向角yaw，转动 y 角度
绕IMU的Y轴旋转：俯仰角pitch，转动 p 角度
绕IMU的X轴旋转：横滚角row，转动 r 角度

另外，横滚roll，俯仰pitch，偏航yaw的实际含义如下图：

2 旋转矩阵

旋转矩阵的知识请先参阅

这里只列出本篇需要用到的3个旋转矩阵，注意这3个旋转矩阵是坐标变换的旋转矩阵。

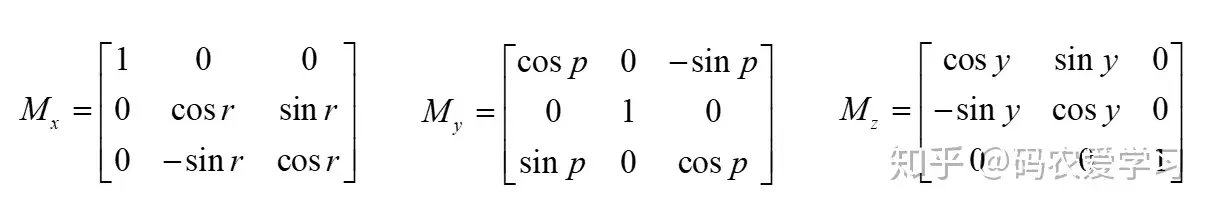
程序表示为：

pitch = asin(-2 * q1 * q3 + 2 * q0* q2)
roll  = atan2(2 * q2 * q3 + 2 * q0 * q1, -2 * q1 * q1 - 2 * q2* q2 + 1)
yaw   = atan2(2*(q1*q2 + q0*q3),q0*q0+q1*q1-q2*q2-q3*q3)

3 欧拉角旋转

欧拉角旋转的知识请先参阅

这里需要说明的是，本篇需要用到的绕着自己运动的轴，以ZYX顺序旋转。

4 加速度计解算姿态角

加速度计测量的是其感受到的加速度，在静止的时候，其本身是没有加速运动的，但因为重力加速度的作用，根据相对运动理论，其感受的加速度与重力加速度正好相反，即读到的数据是竖直向上的。加速度计的英文简写为acc，下面用首字母a代表加速度计数据。

加速度利用静止时刻感受到重力加速度，计算姿态：

当加速度计水平放置，即Z轴竖直向上时，Z轴可以读到1g的数值（g为重力加速度），X轴和Y轴两个方向读到0，可以记作（0，0，g）。
当加速度计旋转一定的姿态时，重力加速度会在加速度的3个轴上产生相应的分量，其本质是大地坐标系下的（0，0，g）在新的加速度计自身坐标系下的坐标，加速度计读到的3个值就是（0，0，g）向量的新坐标。

姿态的旋转选用ZYX顺序的3次旋转方式，则上述描述可表示为：

解这个方程，可以得到roll和pitch角（由于绕Z旋转时，感受到的重力加速度是不变的，因此加速度计无法计算yaw角）

3次旋转过程的分解过程如下图：

5 陀螺仪解算姿态角

陀螺仪测量的绕3个轴转动的角速度，因此，对角速度积分，可以得到角度。陀螺仪的英文简写为gyro，下面用首字母g代表陀螺仪数据。

如下图，IMU在第n个时刻的姿态角度为r、p、y，其含义为IMU坐标系从初始位置，经过绕Z旋转y角度，绕Y旋转p角度，绕X旋转r角度，得到了最终的姿态，此时需要计算下一个时刻(n+1)的姿态。设n+1时刻的姿态角为r+Δr、p+Δp、y+Δy，该姿态也是经历了3次旋转。要想计算n+1时刻的姿态，只要在n时刻姿态的基础上，加上对应的姿态角度变化量即可。姿态角度的变化量可以通过角速度与采用时间周期积分即可。

这里红框中dr/dt等角速度实际是假想的角速度，用于姿态更新，姿态更新是以大地坐标系为参考，而陀螺仪在第n个状态读出的角速度是以它自己所在的坐标系为参考，需要将读到的gyro陀螺数据经过变换，才能用于计算更新第n+1次的姿态。

那dr/dt等角速度该怎样理解呢？看下面这个图，还是将其分解为3次旋转：

首先来看dy/dt，它是3次旋转过程中绕Z轴的yaw角的角速度，3次旋转首先就是绕着Z轴旋转，Z轴方向的单位向量可表示为[0 0 1]T，T表示向量转置，因此[0 0 dy/dt]T表示在图中状态①的坐标中绕Z的角速度。由于之后该坐标系还要经历绕Y和绕X的两次旋转，因此这里[0 0 dy/dt]T角速度在经历两次旋转后，在最终的坐标系(状态③)中的坐标也要经历两次变换。图中的[gx_Z gy_Z gz_Z]T表示3次旋转过程中绕Z轴的yaw角的角速度在最终姿态中的等效转动角速度，实际就是状态①坐标系中绕Z轴的角速度在状态③坐标系中的新的坐标。

同理，dp/dt还需要经历1次旋转变换，而dr/dt不需要经历旋转。

将dy/dt，dp/dt，dr/dt三者都变换到状态③坐标系中的新的坐标相加，实际就是状态③时刻陀螺仪自己读到的gyro数据。

所以，从dr/dt等角速度到陀螺仪读到的角速度gx等的转换关系推导过程如下：

进一步，再把这里的状态③理解为状态n，则根据状态n时刻读到的陀螺仪数据，反解dy/dt等角速度数据，即可更新得到状态n+1的姿态。反解就是求逆矩阵，即：

6 姿态融合

由上面的分析可知，加速度计在静止时刻，根据感受到的重力加速度，可以计算出roll和pitch角，并且角度计算只与当前姿态有关。而陀螺仪是对时间间隔内的角速度积分，得到每一次的角度变换量，累加到上一次的姿态角上，得到新的姿态角，陀螺仪可以计算roll、pitch、yaw三个角。

实际上，加速度仅在静止时刻可以得到较准确的姿态，而陀螺仪仅对转动时的姿态变化敏感，且陀螺仪若本身存在误差，则经过连续的时间积分，误差会不断增大。因此，需要结合两者计算的姿态，进行互补融合。当然，这里只能对roll和pitch融合，因为加速度计没有得到yaw。

K为比例系数，需要根据实际来调整，如选用0.4。

代码

主代码

/* Copyright (C) 2012 Kristian Lauszus, TKJ Electronics. All rights reserved.

 This software may be distributed and modified under the terms of the GNU
 General Public License version 2 (GPL2) as published by the Free Software
 Foundation and appearing in the file GPL2.TXT included in the packaging of
 this file. Please note that GPL2 Section 2[b] requires that all works based
 on this software must also be made publicly available under the terms of
 the GPL2 ("Copyleft").

 Contact information
 -------------------

 Kristian Lauszus, TKJ Electronics
 Web      :  http://www.tkjelectronics.com
 e-mail   :  kristianl@tkjelectronics.com
 */

#include <Wire.h>
#include "Kalman.h" // Source: https://github.com/TKJElectronics/KalmanFilter

#define RESTRICT_PITCH // Comment out to restrict roll to ±90deg instead - please read: http://www.freescale.com/files/sensors/doc/app_note/AN3461.pdf

Kalman kalmanX; // Create the Kalman instances
Kalman kalmanY;

/* IMU Data */
double accX, accY, accZ;
double gyroX, gyroY, gyroZ;
int16_t tempRaw;

double gyroXangle, gyroYangle; // Angle calculate using the gyro only
double compAngleX, compAngleY; // Calculated angle using a complementary filter
double kalAngleX, kalAngleY; // Calculated angle using a Kalman filter

uint32_t timer;
uint8_t i2cData[14]; // Buffer for I2C data

// TODO: Make calibration routine

void setup() {
  Serial.begin(115200);
  Wire.begin();
#if ARDUINO >= 157
  Wire.setClock(400000UL); // Set I2C frequency to 400kHz
#else
  TWBR = ((F_CPU / 400000UL) - 16) / 2; // Set I2C frequency to 400kHz
#endif

  i2cData[0] = 7; // Set the sample rate to 1000Hz - 8kHz/(7+1) = 1000Hz
  i2cData[1] = 0x00; // Disable FSYNC and set 260 Hz Acc filtering, 256 Hz Gyro filtering, 8 KHz sampling
  i2cData[2] = 0x00; // Set Gyro Full Scale Range to ±250deg/s
  i2cData[3] = 0x00; // Set Accelerometer Full Scale Range to ±2g
  while (i2cWrite(0x19, i2cData, 4, false)); // Write to all four registers at once
  while (i2cWrite(0x6B, 0x01, true)); // PLL with X axis gyroscope reference and disable sleep mode

  while (i2cRead(0x75, i2cData, 1));
  if (i2cData[0] != 0x68) { // Read "WHO_AM_I" register
    Serial.print(F("Error reading sensor"));
    while (1);
  }

  delay(100); // Wait for sensor to stabilize

  /* Set kalman and gyro starting angle */
  while (i2cRead(0x3B, i2cData, 6));
  accX = (int16_t)((i2cData[0] << 8) | i2cData[1]);
  accY = (int16_t)((i2cData[2] << 8) | i2cData[3]);
  accZ = (int16_t)((i2cData[4] << 8) | i2cData[5]);

  // Source: http://www.freescale.com/files/sensors/doc/app_note/AN3461.pdf eq. 25 and eq. 26
  // atan2 outputs the value of -π to π (radians) - see http://en.wikipedia.org/wiki/Atan2
  // It is then converted from radians to degrees
#ifdef RESTRICT_PITCH // Eq. 25 and 26
  double roll  = atan2(accY, accZ) * RAD_TO_DEG;
  double pitch = atan(-accX / sqrt(accY * accY + accZ * accZ)) * RAD_TO_DEG;
#else // Eq. 28 and 29
  double roll  = atan(accY / sqrt(accX * accX + accZ * accZ)) * RAD_TO_DEG;
  double pitch = atan2(-accX, accZ) * RAD_TO_DEG;
#endif

  kalmanX.setAngle(roll); // Set starting angle
  kalmanY.setAngle(pitch);
  gyroXangle = roll;
  gyroYangle = pitch;
  compAngleX = roll;
  compAngleY = pitch;

  timer = micros();
}

void loop() {
  /* Update all the values */
  while (i2cRead(0x3B, i2cData, 14));
  accX = (int16_t)((i2cData[0] << 8) | i2cData[1]);
  accY = (int16_t)((i2cData[2] << 8) | i2cData[3]);
  accZ = (int16_t)((i2cData[4] << 8) | i2cData[5]);
  tempRaw = (int16_t)((i2cData[6] << 8) | i2cData[7]);
  gyroX = (int16_t)((i2cData[8] << 8) | i2cData[9]);
  gyroY = (int16_t)((i2cData[10] << 8) | i2cData[11]);
  gyroZ = (int16_t)((i2cData[12] << 8) | i2cData[13]);;

  double dt = (double)(micros() - timer) / 1000000; // Calculate delta time
  timer = micros();

  // Source: http://www.freescale.com/files/sensors/doc/app_note/AN3461.pdf eq. 25 and eq. 26
  // atan2 outputs the value of -π to π (radians) - see http://en.wikipedia.org/wiki/Atan2
  // It is then converted from radians to degrees
#ifdef RESTRICT_PITCH // Eq. 25 and 26
  double roll  = atan2(accY, accZ) * RAD_TO_DEG;
  double pitch = atan(-accX / sqrt(accY * accY + accZ * accZ)) * RAD_TO_DEG;
#else // Eq. 28 and 29
  double roll  = atan(accY / sqrt(accX * accX + accZ * accZ)) * RAD_TO_DEG;
  double pitch = atan2(-accX, accZ) * RAD_TO_DEG;
#endif

  double gyroXrate = gyroX / 131.0; // Convert to deg/s
  double gyroYrate = gyroY / 131.0; // Convert to deg/s

#ifdef RESTRICT_PITCH
  // This fixes the transition problem when the accelerometer angle jumps between -180 and 180 degrees
  if ((roll < -90 && kalAngleX > 90) || (roll > 90 && kalAngleX < -90)) {
    kalmanX.setAngle(roll);
    compAngleX = roll;
    kalAngleX = roll;
    gyroXangle = roll;
  } else
    kalAngleX = kalmanX.getAngle(roll, gyroXrate, dt); // Calculate the angle using a Kalman filter

  if (abs(kalAngleX) > 90)
    gyroYrate = -gyroYrate; // Invert rate, so it fits the restriced accelerometer reading
  kalAngleY = kalmanY.getAngle(pitch, gyroYrate, dt);
#else
  // This fixes the transition problem when the accelerometer angle jumps between -180 and 180 degrees
  if ((pitch < -90 && kalAngleY > 90) || (pitch > 90 && kalAngleY < -90)) {
    kalmanY.setAngle(pitch);
    compAngleY = pitch;
    kalAngleY = pitch;
    gyroYangle = pitch;
  } else
    kalAngleY = kalmanY.getAngle(pitch, gyroYrate, dt); // Calculate the angle using a Kalman filter

  if (abs(kalAngleY) > 90)
    gyroXrate = -gyroXrate; // Invert rate, so it fits the restriced accelerometer reading
  kalAngleX = kalmanX.getAngle(roll, gyroXrate, dt); // Calculate the angle using a Kalman filter
#endif

  gyroXangle += gyroXrate * dt; // Calculate gyro angle without any filter
  gyroYangle += gyroYrate * dt;
  //gyroXangle += kalmanX.getRate() * dt; // Calculate gyro angle using the unbiased rate
  //gyroYangle += kalmanY.getRate() * dt;

  compAngleX = 0.93 * (compAngleX + gyroXrate * dt) + 0.07 * roll; // Calculate the angle using a Complimentary filter
  compAngleY = 0.93 * (compAngleY + gyroYrate * dt) + 0.07 * pitch;

  // Reset the gyro angle when it has drifted too much
  if (gyroXangle < -180 || gyroXangle > 180)
    gyroXangle = kalAngleX;
  if (gyroYangle < -180 || gyroYangle > 180)
    gyroYangle = kalAngleY;

  /* Print Data */
#if 0 // Set to 1 to activate
  Serial.print(accX); Serial.print("\t");
  Serial.print(accY); Serial.print("\t");
  Serial.print(accZ); Serial.print("\t");

  Serial.print(gyroX); Serial.print("\t");
  Serial.print(gyroY); Serial.print("\t");
  Serial.print(gyroZ); Serial.print("\t");

  Serial.print("\t");
#endif

  Serial.print(roll); Serial.print("\t");
  Serial.print(gyroXangle); Serial.print("\t");
  Serial.print(compAngleX); Serial.print("\t");
  Serial.print(kalAngleX); Serial.print("\t");

  Serial.print("\t");

  Serial.print(pitch); Serial.print("\t");
  Serial.print(gyroYangle); Serial.print("\t");
  Serial.print(compAngleY); Serial.print("\t");
  Serial.print(kalAngleY); Serial.print("\t");

#if 0 // Set to 1 to print the temperature
  Serial.print("\t");

  double temperature = (double)tempRaw / 340.0 + 36.53;
  Serial.print(temperature); Serial.print("\t");
#endif

  Serial.print("\r\n");
  delay(2);
}

　　I2C.ino

/* Copyright (C) 2012 Kristian Lauszus, TKJ Electronics. All rights reserved.

 This software may be distributed and modified under the terms of the GNU
 General Public License version 2 (GPL2) as published by the Free Software
 Foundation and appearing in the file GPL2.TXT included in the packaging of
 this file. Please note that GPL2 Section 2[b] requires that all works based
 on this software must also be made publicly available under the terms of
 the GPL2 ("Copyleft").

 Contact information
 -------------------

 Kristian Lauszus, TKJ Electronics
 Web      :  http://www.tkjelectronics.com
 e-mail   :  kristianl@tkjelectronics.com
 */

const uint8_t IMUAddress = 0x68; // AD0 is logic low on the PCB
const uint16_t I2C_TIMEOUT = 1000; // Used to check for errors in I2C communication

uint8_t i2cWrite(uint8_t registerAddress, uint8_t data, bool sendStop) {
  return i2cWrite(registerAddress, &data, 1, sendStop); // Returns 0 on success
}

uint8_t i2cWrite(uint8_t registerAddress, uint8_t *data, uint8_t length, bool sendStop) {
  Wire.beginTransmission(IMUAddress);
  Wire.write(registerAddress);
  Wire.write(data, length);
  uint8_t rcode = Wire.endTransmission(sendStop); // Returns 0 on success
  if (rcode) {
    Serial.print(F("i2cWrite failed: "));
    Serial.println(rcode);
  }
  return rcode; // See: http://arduino.cc/en/Reference/WireEndTransmission
}

uint8_t i2cRead(uint8_t registerAddress, uint8_t *data, uint8_t nbytes) {
  uint32_t timeOutTimer;
  Wire.beginTransmission(IMUAddress);
  Wire.write(registerAddress);
  uint8_t rcode = Wire.endTransmission(false); // Don't release the bus
  if (rcode) {
    Serial.print(F("i2cRead failed: "));
    Serial.println(rcode);
    return rcode; // See: http://arduino.cc/en/Reference/WireEndTransmission
  }
  Wire.requestFrom(IMUAddress, nbytes, (uint8_t)true); // Send a repeated start and then release the bus after reading
  for (uint8_t i = 0; i < nbytes; i++) {
    if (Wire.available())
      data[i] = Wire.read();
    else {
      timeOutTimer = micros();
      while (((micros() - timeOutTimer) < I2C_TIMEOUT) && !Wire.available());
      if (Wire.available())
        data[i] = Wire.read();
      else {
        Serial.println(F("i2cRead timeout"));
        return 5; // This error value is not already taken by endTransmission
      }
    }
  }
  return 0; // Success
}

Kalman.h

/* Copyright (C) 2012 Kristian Lauszus, TKJ Electronics. All rights reserved.

 This software may be distributed and modified under the terms of the GNU
 General Public License version 2 (GPL2) as published by the Free Software
 Foundation and appearing in the file GPL2.TXT included in the packaging of
 this file. Please note that GPL2 Section 2[b] requires that all works based
 on this software must also be made publicly available under the terms of
 the GPL2 ("Copyleft").

 Contact information
 -------------------

 Kristian Lauszus, TKJ Electronics
 Web      :  http://www.tkjelectronics.com
 e-mail   :  kristianl@tkjelectronics.com
 */

#ifndef _Kalman_h_
#define _Kalman_h_

class Kalman {
public:
    Kalman();

    // The angle should be in degrees and the rate should be in degrees per second and the delta time in seconds
    float getAngle(float newAngle, float newRate, float dt);

    void setAngle(float angle); // Used to set angle, this should be set as the starting angle
    float getRate(); // Return the unbiased rate

    /* These are used to tune the Kalman filter */
    void setQangle(float Q_angle);
    /**
     * setQbias(float Q_bias)
     * Default value (0.003f) is in Kalman.cpp. 
     * Raise this to follow input more closely,
     * lower this to smooth result of kalman filter.
     */
    void setQbias(float Q_bias);
    void setRmeasure(float R_measure);

    float getQangle();
    float getQbias();
    float getRmeasure();

private:
    /* Kalman filter variables */
    float Q_angle; // Process noise variance for the accelerometer
    float Q_bias; // Process noise variance for the gyro bias
    float R_measure; // Measurement noise variance - this is actually the variance of the measurement noise

    float angle; // The angle calculated by the Kalman filter - part of the 2x1 state vector
    float bias; // The gyro bias calculated by the Kalman filter - part of the 2x1 state vector
    float rate; // Unbiased rate calculated from the rate and the calculated bias - you have to call getAngle to update the rate

    float P[2][2]; // Error covariance matrix - This is a 2x2 matrix
};

#endif

Kalman.cpp

/* Copyright (C) 2012 Kristian Lauszus, TKJ Electronics. All rights reserved.

 This software may be distributed and modified under the terms of the GNU
 General Public License version 2 (GPL2) as published by the Free Software
 Foundation and appearing in the file GPL2.TXT included in the packaging of
 this file. Please note that GPL2 Section 2[b] requires that all works based
 on this software must also be made publicly available under the terms of
 the GPL2 ("Copyleft").

 Contact information
 -------------------

 Kristian Lauszus, TKJ Electronics
 Web      :  http://www.tkjelectronics.com
 e-mail   :  kristianl@tkjelectronics.com
 */

#include "Kalman.h"

Kalman::Kalman() {
    /* We will set the variables like so, these can also be tuned by the user */
    Q_angle = 0.001f;
    Q_bias = 0.003f;
    R_measure = 0.03f;

    angle = 0.0f; // Reset the angle
    bias = 0.0f; // Reset bias

    P[0][0] = 0.0f; // Since we assume that the bias is 0 and we know the starting angle (use setAngle), the error covariance matrix is set like so - see: http://en.wikipedia.org/wiki/Kalman_filter#Example_application.2C_technical
    P[0][1] = 0.0f;
    P[1][0] = 0.0f;
    P[1][1] = 0.0f;
};

// The angle should be in degrees and the rate should be in degrees per second and the delta time in seconds
float Kalman::getAngle(float newAngle, float newRate, float dt) {
    // KasBot V2  -  Kalman filter module - http://www.x-firm.com/?page_id=145
    // Modified by Kristian Lauszus
    // See my blog post for more information: http://blog.tkjelectronics.dk/2012/09/a-practical-approach-to-kalman-filter-and-how-to-implement-it

    // Discrete Kalman filter time update equations - Time Update ("Predict")
    // Update xhat - Project the state ahead
    /* Step 1 */
    rate = newRate - bias;
    angle += dt * rate;

    // Update estimation error covariance - Project the error covariance ahead
    /* Step 2 */
    P[0][0] += dt * (dt*P[1][1] - P[0][1] - P[1][0] + Q_angle);
    P[0][1] -= dt * P[1][1];
    P[1][0] -= dt * P[1][1];
    P[1][1] += Q_bias * dt;

    // Discrete Kalman filter measurement update equations - Measurement Update ("Correct")
    // Calculate Kalman gain - Compute the Kalman gain
    /* Step 4 */
    float S = P[0][0] + R_measure; // Estimate error
    /* Step 5 */
    float K[2]; // Kalman gain - This is a 2x1 vector
    K[0] = P[0][0] / S;
    K[1] = P[1][0] / S;

    // Calculate angle and bias - Update estimate with measurement zk (newAngle)
    /* Step 3 */
    float y = newAngle - angle; // Angle difference 
    /* Step 6 */
    angle += K[0] * y;
    bias += K[1] * y;

    // Calculate estimation error covariance - Update the error covariance
    /* Step 7 */
    float P00_temp = P[0][0];
    float P01_temp = P[0][1];

    P[0][0] -= K[0] * P00_temp;
    P[0][1] -= K[0] * P01_temp;
    P[1][0] -= K[1] * P00_temp;
    P[1][1] -= K[1] * P01_temp;

    return angle;
};

void Kalman::setAngle(float angle) { this->angle = angle; }; // Used to set angle, this should be set as the starting angle
float Kalman::getRate() { return this->rate; }; // Return the unbiased rate

/* These are used to tune the Kalman filter */
void Kalman::setQangle(float Q_angle) { this->Q_angle = Q_angle; };
void Kalman::setQbias(float Q_bias) { this->Q_bias = Q_bias; };
void Kalman::setRmeasure(float R_measure) { this->R_measure = R_measure; };

float Kalman::getQangle() { return this->Q_angle; };
float Kalman::getQbias() { return this->Q_bias; };
float Kalman::getRmeasure() { return this->R_measure; };

标签：angle,Kalman,卡尔曼滤波,float,slam14,ardunio,print,Serial,dt
From： https://www.cnblogs.com/gooutlook/p/16965044.html

slam14(1) v4_1 卡尔曼滤波3 使用例子和代码 ardunio mpu6050

代码