原文:Hands-On Reinforcement Learning with Python
译者:飞龙
本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。
不要担心自己的形象,只关心如何实现目标。——《原则》,生活原则 2.3.c
一、强化学习导论
强化学习(RL)是机器学习的一个分支,其中学习是通过与环境交互来进行的。 这是面向目标的学习,不教导学习器采取什么行动; 相反,学习器从其行动的结果中学习。 随着各种算法的迅速发展,它是人工智能(AI)中最活跃的研究领域之一。
在本章中,您将了解以下内容:
- RL 的基本概念
- RL 算法
- 智能体环境接口
- RL 环境的类型
- RL 平台
- RL 的应用
什么是 RL?
考虑到您正在教狗接球,但是您不能明确地教狗接球; 取而代之的是,您将只扔一个球,每次狗抓到球时,您都将给它一个曲奇。 如果无法接住球,则不会提供曲奇。 狗将找出使它收到 Cookie 的动作,然后重复这些动作。
同样,在 RL 环境中,您不会教智能体做什么或如何做,而是会针对智能体执行的每个操作给予奖励。 奖励可以是正面的或负面的。 然后,智能体将开始执行使其获得正面奖励的操作。 因此,这是一个反复试验的过程。 在先前的类比中,狗代表智能体。 接球时给狗送饼干是一种积极的奖励,而不送饼干则是一种消极的奖励。
奖励可能会延迟。 您可能无法在每一步都获得奖励。 只有在任务完成后才能给予奖励。 在某些情况下,您会在每一步中获得奖励,以查明您是否犯了任何错误。
想象一下,您想教一个机器人走路而不会撞上山而被卡住,但是您不会明确地教它不要朝着山的方向走:
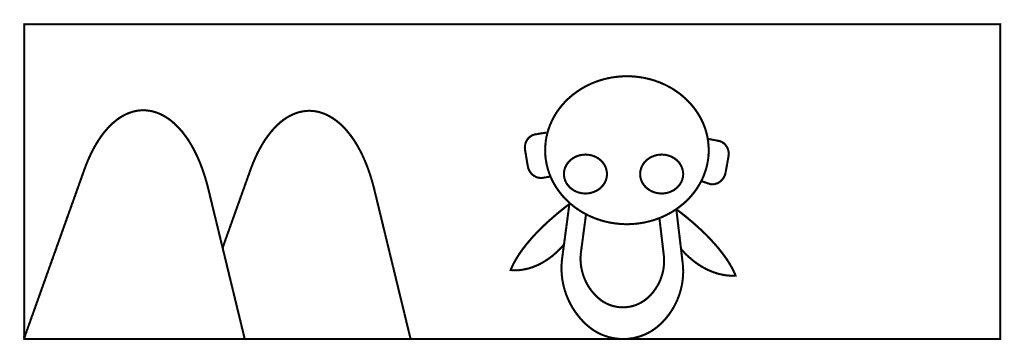
相反,如果机器人撞到并卡在山上,您将获得 10 分,这样机器人就会知道撞上山会产生负奖励,并且不会再次朝该方向前进:
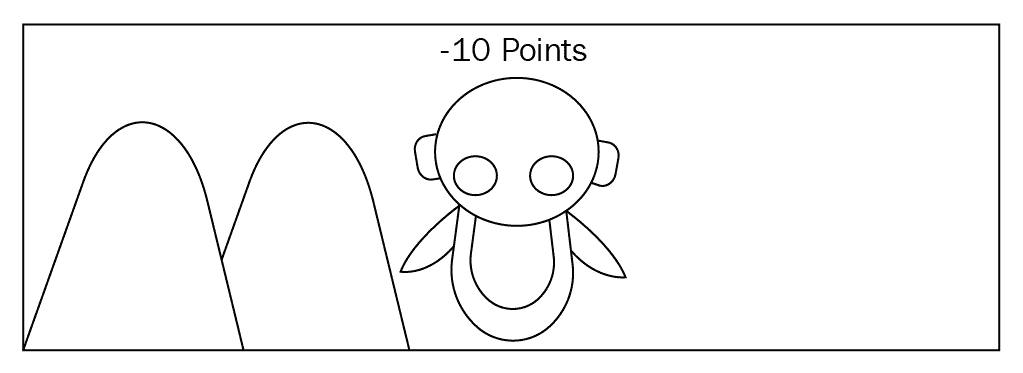
如果机器人在正确的方向上行走而不被卡住,您将获得 20 分。 因此,机器人将了解哪条道路是正确的,并会通过朝正确的方向努力来最大化回报:

RL 智能体可以探索可能提供良好奖励的不同动作,也可以利用(使用)导致良好奖励的先前动作。 如果 RL 智能体探索不同的行动,则该智能体很可能会收到较差的报酬,因为所有行动都不会成为最佳行动。 如果 RL 智能体仅利用已知的最佳动作,那么也有可能会错过最佳动作,这可能会提供更好的回报。 探索与利用之间总是要权衡取舍。 我们不能同时进行探索和利用。 在接下来的章节中,我们将详细讨论探索与利用难题。
RL 算法
典型的 RL 算法涉及的步骤如下:
- 首先,智能体通过执行操作与环境进行交互
- 智能体执行动作并从一种状态转移到另一种状态
- 然后,智能体将根据其执行的动作获得奖励
- 根据奖励,智能体将了解该操作是好是坏
- 如果该动作是好的,即如果该智能体收到了积极的报酬,则该智能体将更喜欢执行该动作,否则该智能体将尝试执行导致积极报酬的其他动作。 所以这基本上是一个反复试验的学习过程
RL 与其他 ML 范式有何不同
在监督学习中,机器(智能体)从训练数据中学习,该训练数据具有一组标记的输入和输出。 目的是模型外推并概括其学习,以便可以很好地应用于看不见的数据。 有一个外部主管,他具有完整的环境知识基础并监督智能体以完成一项任务。
考虑一下我们刚才讨论的狗类比; 在监督学习中,要教狗接球,我们将通过指定向左转,向右走,前进五个步骤,接球等等来明确地教它。 但是在 RL 中,我们只是扔一个球,每当狗抓到球时,我们都会给它一个曲奇(奖励)。 因此,狗将学会接球,这意味着它收到了饼干。
在无监督学习中,我们为模型提供只有一组输入的训练数据。 模型学习确定输入中的隐藏模式。 有一个普遍的误解,认为 RL 是一种无监督的学习,但事实并非如此。 在无监督学习中,模型学习隐藏的结构,而在 RL 中,模型通过最大化奖励来学习。 假设我们想向用户推荐新电影。 无监督学习会分析用户观看过的相似电影并建议电影,而 RL 会不断从用户那里收到反馈,了解他的电影偏好,并在此基础上建立知识库并建议新电影。
还有另一种称为半监督学习的学习,它基本上是有监督学习和无监督学习的结合。 它涉及对标记和未标记数据的函数估计,而 RL 本质上是智能体与其环境之间的相互作用。 因此,RL 与所有其他机器学习范例完全不同。
RL 的元素
RL 的元素在以下各节中显示。
智能体
智能体是做出明智决策的软件程序,它们基本上是 RL 的学习器。 智能体通过与环境互动来采取行动,他们会根据自己的行动获得奖励,例如,在视频游戏中导航的超级马里奥。
策略函数
策略定义环境中智能体的行为。 智能体决定执行哪种操作的方式取决于策略。 假设您想在家中到达办公室; 到达办公室的路线会有所不同,有些路线是捷径,有些路线很长。 这些路线被称为策略,因为它们代表了我们选择采取行动以达到目标的方式。 策略通常用符号π表示。 策略可以采用查找表或复杂的搜索过程的形式。
值函数
值函数表示智能体处于特定状态的程度如何。 它取决于策略,通常用v(s)表示。 它等于智能体从初始状态开始收到的总预期奖励。 可以有多个值函数。 最优值函数是与其他值函数相比在所有状态下具有最高值的函数。 同样,最优策略是具有最优值函数的策略。
模型
模型是智能体程序对环境的表示。 学习可以分为两种类型:基于模型的学习和无模型的学习。 在基于模型的学习中,智能体利用先前学习的信息来完成任务,而在无模型的学习中,智能体仅依靠反复试验的经验来执行正确的操作。 假设您想在家中更快地到达办公室。 在基于模型的学习中,您只需使用以前学习的经验(地图)即可更快地到达办公室,而在无模型的学习中,您将不会使用以前的经验,而是尝试所有不同的路线并选择更快的路线。
智能体环境接口
智能体是指一次执行A[t],t移动的动作的软件智能体。 从一种状态S[t],到另一种状态S[t + 1]。 基于行为,智能体从环境中获得数值奖励R。 最终,RL 就是寻找可以增加数值奖励的最佳行动:

让我们通过迷宫游戏来理解 RL 的概念:

迷宫的目的是到达目的地而不会卡在障碍物上。 这是工作流程:
- 智能体是穿越迷宫的人,这是我们的软件程序/ RL 算法
- 环境是迷宫
- 状态是智能体当前位于迷宫中的位置
- 智能体通过从一种状态转移到另一种状态来执行动作
- 当智能体的动作没有遇到任何障碍时,它会获得正向奖励;当智能体的行为没有遇到任何障碍时,它会得到负向奖励,因此它无法到达目的地
- 目的是探查迷宫并到达目的地
RL 环境的类型
智能体与之交互的所有事物都称为环境。 环境是外部世界。 它包含智能体之外的所有内容。 有不同类型的环境,将在下一节中介绍。
确定性环境
当我们基于当前状态知道结果时,就可以说环境是确定性的。 例如,在国际象棋游戏中,我们知道移动任何玩家的确切结果。
随机环境
当我们无法根据当前状态确定结果时,就说环境是随机的。 不确定性将更大。 例如,我们永远不知道掷骰子时会显示多少数字。
完全可观察的环境
当智能体可以始终确定系统状态时,称为完全可观察。 例如,在国际象棋游戏中,系统状态,即所有玩家在国际象棋棋盘上的位置始终可用,因此玩家可以做出最佳决策。
部分可观察的环境
当智能体无法始终确定系统状态时,称为部分可观察。 例如,在扑克游戏中,我们不知道对手拥有的牌。
离散环境
当只有有限状态的动作可用于从一种状态转移到另一种状态时,它称为离散环境。 例如,在国际象棋游戏中,我们只有一组有限的动作。
连续环境
当动作的无限状态可以从一种状态转移到另一种状态时,称为连续环境。 例如,我们有多条路线可用于从源头到目的地的旅行。
情景和非情景环境
情景环境也称为非顺序环境。 在情景环境中,主体的当前动作不会影响将来的动作,而在非周期性环境中,主体的当前动作会影响未来的动作,也称为顺序环境。 也就是说,主体在剧集环境中执行独立的任务,而在非周期性环境中,所有主体的动作都是相关的。
单智能体和多智能体环境
顾名思义,单智能体环境只有一个智能体,多智能体环境有多个智能体。 在执行复杂任务时,广泛使用多智能体环境。 在完全不同的环境中将存在不同的智能体。 不同环境中的智能体将彼此通信。 由于多主体环境具有更大的不确定性,因此它几乎是随机的。
RL 平台
RL 平台用于在环境中模拟,构建,渲染和试验我们的 RL 算法。 有很多可用的 RL 平台,如以下各节所述。
OpenAI Gym 和 Universe
OpenAI Gym 是用于构建,评估和比较 RL 算法的工具包。 它与在 TensorFlow,Theano,Keras 等任何框架中编写的算法兼容。 它很容易理解。 它不对智能体的结构做任何假设,并提供了所有 RL 任务的接口。
OpenAI Universe 是 OpenAI Gym 的扩展。 它提供了在各种简单到实时复杂环境中训练和评估智能体的能力。 它可以无限制地访问许多游戏环境。 使用 Universe,可以通过在虚拟网络计算远程桌面后自动启动程序来将任何程序转换为 Gym 环境,而无需访问程序内部,源代码或 API,因为 Universe 可以工作。
DeepMind Lab
DeepMind Lab 是另一个基于 AI 智能体的惊人研究平台。 它提供了一个丰富的模拟环境,可以作为运行几种 RL 算法的实验室。 它是高度可定制和可扩展的。 视觉效果非常丰富,科幻风格且逼真。
RLGlue
RL-Glue 提供了一个接口,用于将智能体,环境和程序连接在一起,即使它们是用不同的编程语言编写的。 它具有与他人共享您的智能体和环境以在您的工作之上进行构建的能力。 由于这种兼容性,可重用性大大提高了。
Malmo 计划
Malmo 计划是微软在 Minecraft 之上构建的另一个 AI 实验平台。 它为自定义环境提供了良好的灵活性。 它与复杂的环境集成在一起。 它还允许超频,这使程序员能够比标准 Minecraft 更快地播放场景。 但是,与 Open AI Universe 不同,Malmo 当前仅提供 Minecraft 游戏环境。
ViZDoom
顾名思义,ViZDoom 是一个基于 Doom 的 AI 平台。 它为多智能体提供支持,并提供竞争环境来测试智能体。 但是,ViZDoom 仅支持 Doom 游戏环境。 它提供了屏幕外渲染以及单人和多人游戏支持。
RL 的应用
凭借更大的进步和研究,RL 已在从玩计算机游戏到汽车自动化的多个领域迅速发展了日常应用。 以下各节列出了一些 RL 应用。
教育
许多在线教育平台都在使用 RL 为每个学生提供个性化的内容。 有些学生可能会从视频内容中学习得更好,一些学生可能会通过做项目来学习,而有些人可能会从笔记中学习。 RL 用于根据每个学生的学习风格来调整个性化的教育内容,并且可以根据用户的行为进行动态更改。
医药保健
RL 在医学和卫生保健方面有无数的应用; 其中一些包括个性化医疗,基于医学图像的诊断,获得临床决策中的治疗策略,医学图像分割等。
制造业
在制造中,智能机器人用于将物体放置在正确的位置。 如果它失败或无法成功将对象放置在正确的位置,它将记住该对象并训练自己以更高的精度执行此操作。 使用智能智能体将减少人工成本并提高表现。
库存管理
RL 广泛用于库存管理,这是一项至关重要的业务活动。 其中一些活动包括供应链管理,需求预测和处理多个仓库操作(例如将产品放置在仓库中以有效管理空间)。 DeepMind 的 Google 研究人员开发了 RL 算法,可有效降低其数据中心的能耗。
金融
RL 被广泛用于金融投资组合管理,这是将资金不断重新分配给不同金融产品的过程,也用于商业交易市场的预测和交易。 JP Morgan 已成功使用 RL 为大订单提供更好的交易执行结果。
自然语言处理与计算机视觉
凭借深度学习和 RL 的统一能力,深度强化学习(DRL)在自然语言处理(NLP)和计算机视觉(CV)领域中得到了极大的发展。。 DRL 已用于文本摘要,信息提取,机器翻译和图像识别,比当前系统具有更高的准确率。
总结
在本章中,我们学习了 RL 的基础知识以及一些关键概念。 我们了解了 RL 的不同元素和 RL 环境的不同类型。 我们还介绍了各种可用的 RL 平台以及 RL 在各个领域中的应用。
在下一章第 2 章,“OpenAI 和 TensorFlow 入门”中,我们将学习 OpenAI 和 TensorFlow 的基础知识以及如何安装 OpenAI 和 TensorFlow,然后模拟环境并教给智能体如何在环境中学习。
问题
问题列表如下:
- 什么是强化学习?
- RL 与其他 ML 范式有何不同?
- 什么是智能体,智能体如何学习?
- 策略函数和值函数有什么区别?
- 基于模型的学习与基于模型的学习有什么区别?
- RL 中有哪些不同类型的环境?
- OpenAI Universe 与其他 RL 平台有何不同?
- RL 有哪些应用?
进一步阅读
二、OpenAI 和 TensorFlow 入门
OpenAI 是由 Elon Musk 和 Sam Altman 创立的非营利性,开源人工智能(AI)研究公司,旨在构建通用 AI。 他们是由顶级行业领导者和顶尖公司赞助的。 OpenAI 具有 Gym 和 Universe 两种样式,我们可以使用它们模拟现实环境,构建强化学习(RL)算法,并在这些环境中测试我们的智能体。 TensorFlow 是 Google 的开源机器学习库,已广泛用于数值计算。 在接下来的章节中,我们将使用 OpenAI 和 TensorFlow 来构建和评估强大的 RL 算法。
在本章中,您将了解以下内容:
- 通过安装 Anaconda,Docker,OpenAI Gym 和 Universe 和 TensorFlow 设置机器
- 使用 OpenAI Gym 和 Universe 模拟环境
- 训练机器人走路
- 构建一个视频游戏机器人
- TensorFlow 的基本原理
- 使用 TensorBoard
配置机器
安装 OpenAI 并不是一件容易的事。 要设置和运行系统,必须正确遵循一组步骤。 现在,让我们看看如何设置我们的机器并安装 OpenAI Gym 和 Universe。
安装 Anaconda
本书中的所有示例均使用 Anaconda 版本的 Python。 Anaconda 是 Python 的开源发行版。 它被广泛用于科学计算和处理大量数据。 它提供了一个出色的包管理环境。 它提供对 Windows,macOS 和 Linux 的支持。 Anaconda 随附安装了 Python 以及用于科学计算的流行包,例如 NumPy,SciPy 等。
要下载 Anaconda,请访问这里,您将在此处看到用于下载用于不同平台的 Anaconda 的选项。
如果使用 Windows 或 Mac,则可以根据计算机架构直接下载图形安装程序,然后使用图形安装程序进行安装。
如果您使用的是 Linux,请按照以下步骤操作:
- 打开终端并输入以下内容以下载 Anaconda:
wget https://repo.continuum.io/archive/Anaconda3-5.0.1-Linux-x86_64.sh
- 完成后,我们可以通过以下命令安装 Anaconda:
bash Anaconda3-5.0.1-Linux-x86_64.sh
成功安装 Anaconda 后,我们需要创建一个新的 Anaconda 环境,该环境基本上是一个虚拟环境。 虚拟环境有什么需求? 假设您正在使用 Aum 版本 1.14 的项目 A 和使用 NumPy 版本 1.13 的项目 B。 因此,要进行项目 B,您可以降级 NumPy 或重新安装 Anaconda。 在每个项目中,我们使用具有不同版本的不同库,这些库不适用于其他项目。 我们使用虚拟环境来代替降级或升级版本或为新项目每次重新安装 Anaconda。 这为当前项目创建了一个隔离的环境,因此每个项目可以具有自己的依赖,并且不会影响其他项目。 我们将使用以下命令创建这样的环境,并将我们的环境命名为universe:
conda create --name universe python=3.6 anaconda
我们可以使用以下命令激活环境:
source activate universe
安装 Docker
安装 Anaconda 之后,我们需要安装 Docker。 Docker 使将应用部署到生产变得容易。 假设您在具有 TensorFlow 和其他一些库的localhost中构建了一个应用,并且要将应用部署到服务器中。 您将需要在服务器上安装所有这些依赖项。 但是使用 Docker,我们可以将应用及其依赖项打包在一起,这称为容器,并且我们可以在服务器上运行应用而无需在打包的 Docker 容器中使用任何外部依赖项。 OpenAI 不支持 Windows,因此要在 Windows 中安装 OpenAI,我们需要使用 Docker。 而且,大多数 OpenAI Universe 环境都需要 Docker 来模拟环境。 现在让我们看看如何安装 Docker。
要下载 Docker,请转至这里,您将在其中看到一个名为“Get Docker”的选项。 如果选择该选项,则将看到不同操作系统的选项。 如果使用 Windows 或 Mac,则可以下载 Docker 并直接使用图形安装程序进行安装。
如果您使用的是 Linux,请按照以下步骤操作:
打开您的终端并输入以下内容:
sudo apt-get install \
apt-transport-https \
ca-certificates \
curl \
software-properties-common
然后输入:
curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add -
然后输入:
sudo add-apt-repository \
"deb [arch=amd64] https://download.docker.com/linux/ubuntu \
$(lsb_release -cs) \
stable"
最后,输入:
sudo apt-get update
sudo apt-get install docker-ce
我们需要成为 Docker 用户组的成员才能开始使用 Docker。 您可以通过以下命令加入 Docker 用户组:
sudo adduser $(whoami) docker
newgrp docker
groups
我们可以通过运行内置的hello-world程序来测试 Docker 的安装:
sudo service docker start
sudo docker run hello-world
为了避免每次使用sudo来使用 Docker,我们可以使用以下命令:
sudo groupadd docker
sudo usermod -aG docker $USER
sudo reboot
安装 OpenAI Gym 和 Universe
现在让我们看看如何安装 OpenAI Gym 和 Universe。 在此之前,我们需要安装几个依赖项。 首先,让我们使用以下命令激活刚刚创建的conda环境:
source activate universe
然后,我们将安装以下依赖项:
sudo apt-get update
sudo apt-get install golang libcupti-dev libjpeg-turbo8-dev make tmux htop chromium-browser git cmake zlib1g-dev libjpeg-dev xvfb libav-tools xorg-dev python-opengl libboost-all-dev libsdl2-dev swig
conda install pip six libgcc swig
conda install opencv
在本书中,我们将使用gym版本0.7.0,因此您可以使用pip直接安装gym,如下所示:
pip install gym==0.7.0
或者,您可以克隆gym存储库并通过以下命令安装最新版本:
cd ~
git clone https://github.com/openai/gym.git
cd gym
pip install -e '.[all]'
前面的命令将获取gym存储库并以包的形式安装gym,如以下屏幕截图所示:

常见错误修复
在安装 Gym 时,您很可能会遇到以下任何错误。 如果出现这些错误,只需运行以下命令并尝试重新安装:
Failed building wheel for pachi-py或Failed building wheel for pachi-py atari-py:
sudo apt-get update
sudo apt-get install xvfb libav-tools xorg-dev libsdl2-dev swig cmake
Failed building wheel for mujoco-py:
git clone https://github.com/openai/mujoco-py.git
cd mujoco-py
sudo apt-get update
sudo apt-get install libgl1-mesa-dev libgl1-mesa-glx libosmesa6-dev python3-pip python3-numpy python3-scipy
pip3 install -r requirements.txt
sudo python3 setup.py install
Error: command 'gcc' failed with exit status 1:
sudo apt-get update
sudo apt-get install python-dev
sudo apt-get install libevent-dev
同样,我们可以通过获取universe存储库并将universe作为包安装来安装 OpenAI Universe:
cd ~
git clone https://github.com/openai/universe.git
cd universe
pip install -e .
以下屏幕快照显示了安装:

如前所述,Open AI Universe 需要 Docker,因为大多数 Universe 环境都在 Docker 容器中运行。
因此,让我们构建一个 Docker 镜像并将其命名为universe:
docker build -t universe .
构建 Docker 镜像后,我们运行以下命令,该命令从 Docker 镜像启动容器:
docker run --privileged --rm -it -p 12345:12345 -p 5900:5900 -e DOCKER_NET_HOST=172.17.0.1 universe /bin/bash
OpenAI Gym
借助 OpenAI Gym,我们可以模拟各种环境,并开发,评估和比较 RL 算法。 现在让我们了解如何使用 Gym。
基本模拟
让我们看看如何模拟基本的购物车杆环境:
- 首先,让我们导入库:
import gym
- 下一步是使用
make函数创建一个仿真实例:
env = gym.make('CartPole-v0')
- 然后,我们应该使用
reset方法初始化环境:
env.reset()
- 然后,我们可以循环执行一些时间步骤,并在每个步骤渲染环境:
for _ in range(1000):
env.render()
env.step(env.action_space.sample())
完整的代码如下:
import gym
env = gym.make('CartPole-v0')
env.reset()
for _ in range(1000):
env.render()
env.step(env.action_space.sample())
如果运行前面的程序,则可以看到输出,该输出显示了购物车杆环境:

OpenAI Gym 提供了许多模拟环境,用于训练,评估和构建我们的智能体。 我们可以通过检查其网站或输入以下内容来检查可用的环境,这些将列出可用的环境:
from gym import envs
print(envs.registry.all())
由于 Gym 提供了不同的有趣环境,因此让我们模拟一个赛车环境,如下所示:
import gym
env = gym.make('CarRacing-v0')
env.reset()
for _ in range(1000):
env.render()
env.step(env.action_space.sample())
您将获得如下输出:

训练机器人走路
现在,让我们学习如何使用 Gym 训练机器人走路以及一些基础知识。
该策略是当机器人向前移动时将获得X点作为奖励,如果机器人无法移动,则会减少Y点。 因此,机器人将在最大化奖励的情况下学习行走。
首先,我们将导入库,然后通过make函数创建一个仿真实例。 Open AI Gym 提供了一个称为BipedalWalker-v2的环境,用于在简单的地形中训练机器人智能体:
import gym
env = gym.make('BipedalWalker-v2')
然后,对于每个剧集(初始状态和最终状态之间的智能体程序-环境交互),我们将使用reset方法初始化环境:
for episode in range(100):
observation = env.reset()
然后,我们将循环并渲染环境:
for i in range(10000):
env.render()
我们从环境的行动空间中抽样随机行动。 每个环境都有一个动作空间,其中包含所有可能的有效动作:
action = env.action_space.sample()
对于每个操作步骤,我们将记录observation,reward,done和info:
observation, reward, done, info = env.step(action)
observation是代表观察环境的对象。 例如,机器人在地形中的状态。
reward是上一动作获得的奖励。 例如,机器人成功前进所获得的奖励。
done是布尔值; 如果为真,则表明该剧集已经完成(也就是说,机器人学会了行走或完全失败)。 剧集完成后,我们可以使用env.reset()初始化下一个剧集的环境。
info是可用于调试的信息。
当done为true时,我们打印该剧集采取的时间步长并中断当前剧集:
if done:
print("{} timesteps taken for the Episode".format(i+1))
break
完整的代码如下:
import gym
env = gym.make('BipedalWalker-v2')
for i_episode in range(100):
observation = env.reset()
for t in range(10000):
env.render()
print(observation)
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
if done:
print("{} timesteps taken for the episode".format(t+1))
break
输出显示在以下屏幕截图中:

OpenAI Universe
OpenAI Universe 提供了广泛的现实游戏环境。 它是 OpenAI Gym 的扩展。 它提供了在各种简单到实时复杂环境中训练和评估智能体的能力。 它可以无限制地访问许多游戏环境。
构建一个视频游戏机器人
让我们学习如何构建一个可以玩赛车游戏的视频游戏机器人。 我们的目标是赛车必须前进,而不会卡在任何障碍物上或撞到其他赛车上。
首先,我们导入必要的库:
import gym
import universe # register universe environment
import random
然后,我们使用make函数模拟赛车环境:
env = gym.make('flashgames.NeonRace-v0')
env.configure(remotes=1) #automatically creates a local docker container
让我们创建用于移动汽车的变量:
# Move left
left = [('KeyEvent', 'ArrowUp', True), ('KeyEvent', 'ArrowLeft', True),
('KeyEvent', 'ArrowRight', False)]
#Move right
right = [('KeyEvent', 'ArrowUp', True), ('KeyEvent', 'ArrowLeft', False),
('KeyEvent', 'ArrowRight', True)]
# Move forward
forward = [('KeyEvent', 'ArrowUp', True), ('KeyEvent', 'ArrowRight', False),
('KeyEvent', 'ArrowLeft', False), ('KeyEvent', 'n', True)]
我们将初始化一些其他变量:
# We use turn variable for deciding whether to turn or not
turn = 0
# We store all the rewards in rewards list
rewards = []
#we will use buffer as some threshold
buffer_size = 100
#we will initially set action as forward, which just move the car forward #without any turn
action = forward
现在,让我们的游戏智能体在无限循环中玩,该循环基于与环境的交互持续执行动作:
while True:
turn -= 1
# Let us say initially we take no turn and move forward.
# We will check value of turn, if it is less than 0
# then there is no necessity for turning and we just move forward.
if turn <= 0:
action = forward
turn = 0
然后,我们使用env.step()一次性执行一项操作(暂时向前移动):
action_n = [action for ob in observation_n]
observation_n, reward_n, done_n, info = env.step(action_n)
对于每个时间步,我们将结果记录在observation_n,reward_n,done_n和info变量中:
observation _n:汽车状态reward_n:如果汽车成功前进但没有卡在障碍物上,则通过上一个动作获得奖励done_n:这是一个布尔值; 如果游戏结束,它将设置为trueinfo_n:用于调试目的
显然,智能体(汽车)无法在整个游戏中前进; 它需要转弯,避免障碍物,并且还会撞到其他车辆。 但是它必须确定是否应该转弯,如果需要转弯,则应朝哪个方向转弯。
首先,我们将计算到目前为止获得的奖励的平均值; 如果是0,则很明显我们在前进时被卡在某处,我们需要转弯。 然后,我们需要转向哪个方向? 您是否还记得我们在第 1 章,“强化学习简介”中研究的策略函数。
关于同一概念,我们这里有两个策略:一个是左转,另一个是右转。 我们将在这里采取随机策略,并计算出奖励并加以改善。
我们将生成一个随机数,如果它小于0.5,那么我们将获得一个右数,否则我们将得到一个左数。 稍后,我们将更新奖励,并根据奖励,了解哪个方向最佳:
if len(rewards) >= buffer_size:
mean = sum(rewards)/len(rewards)
if mean == 0:
turn = 20
if random.random() < 0.5:
action = right
else:
action = left
rewards = []
然后,对于每个剧集(例如游戏结束),我们使用env.render()重新初始化环境(从头开始游戏):
env.render()
完整的代码如下:
import gym
import universe # register universe environment
import random
env = gym.make('flashgames.NeonRace-v0')
env.configure(remotes=1) # automatically creates a local docker container
observation_n = env.reset()
##Declare actions
#Move left
left = [('KeyEvent', 'ArrowUp', True), ('KeyEvent', 'ArrowLeft', True),
('KeyEvent', 'ArrowRight', False)]
#move right
right = [('KeyEvent', 'ArrowUp', True), ('KeyEvent', 'ArrowLeft', False),
('KeyEvent', 'ArrowRight', True)]
# Move forward
forward = [('KeyEvent', 'ArrowUp', True), ('KeyEvent', 'ArrowRight', False),
('KeyEvent', 'ArrowLeft', False), ('KeyEvent', 'n', True)]
#Determine whether to turn or not
turn = 0
#store rewards in a list
rewards = []
#use buffer as a threshold
buffer_size = 100
#initial action as forward
action = forward
while True:
turn -= 1
if turn <= 0:
action = forward
turn = 0
action_n = [action for ob in observation_n]
observation_n, reward_n, done_n, info = env.step(action_n)
rewards += [reward_n[0]]
if len(rewards) >= buffer_size:
mean = sum(rewards)/len(rewards)
if mean == 0:
turn = 20
if random.random() < 0.5:
action = right
else:
action = left
rewards = []
env.render()
如果运行该程序,则可以看到汽车如何学习运动而不会被卡住或撞到其他车辆:

TensorFlow
TensorFlow 是 Google 的开源软件库,已广泛用于数值计算。 它被广泛用于构建深度学习模型,并且是机器学习的一个子集。 它使用可以在许多不同平台上共享和执行的数据流图。 张量只是多维数组,因此,当我们说 TensorFlow 时,它实际上是计算图中的多维数组(张量)的流。
安装 Anaconda 后,安装 TensorFlow 变得非常简单。 无论使用什么平台,都可以通过键入以下命令轻松安装 TensorFlow:
source activate universe
conda install -c conda-forge tensorflow
在安装 TensorFlow 之前,请不要忘记激活universe环境。
我们可以通过简单地运行以下Hello World程序来检查 TensorFlow 安装是否成功:
import tensorflow as tf
hello = tf.constant("Hello World")
sess = tf.Session()
print(sess.run(hello))
变量,常量和占位符
变量,常量和占位符是 TensorFlow 的基本元素。 但是,这三者之间总是存在混淆。 让我们逐一查看每个元素,并了解它们之间的区别。
变量
变量是用于存储值的容器。 变量将用作计算图中其他几个操作的输入。 我们可以使用tf.Variable()函数创建 TensorFlow 变量。 在下面的示例中,我们定义一个具有随机正态分布值的变量,并将其命名为weights:
weights = tf.Variable(tf.random_normal([3, 2], stddev=0.1), name="weights")
但是,在定义变量后,我们需要使用tf.global_variables_initializer()方法显式创建初始化操作,该方法将为变量分配资源。
常量
常量与变量不同,不能更改其值。 常量是不可变的。 一旦为它们分配了值,就不能在整个过程中进行更改。 我们可以使用tf.constant()函数创建常量:
x = tf.constant(13)
占位符
可以将占位符视为变量,在其中仅定义类型和大小而不会分配值。 占位符定义为无值。 占位符的值将在运行时输入。 占位符有一个可选参数shape,它指定数据的维数。 如果shape设置为None,那么我们可以在运行时提供任意大小的数据。 可以使用tf.placeholder()函数定义占位符:
x = tf.placeholder("float", shape=None)
简单来说,我们使用tf.Variable存储数据,并使用tf.placeholder馈送外部数据。
计算图
TensorFlow 中的所有内容都将表示为由节点和边组成的计算图,其中节点是数学运算(例如加法,乘法等),而边是张量。 拥有计算图非常有效地优化了资源,并且还促进了分布式计算。
假设我们有节点B,其输入取决于节点A的输出; 这种依赖关系称为直接依赖关系。
例如:
A = tf.multiply(8,5)
B = tf.multiply(A,1)
当节点B的输入不依赖于节点A时,称为间接依赖。
例如:
A = tf.multiply(8,5)
B = tf.multiply(4,3)
因此,如果我们能够理解这些依赖性,则可以在可用资源中分配独立的计算并减少计算时间。
每当我们导入 TensorFlow 时,都会自动创建一个默认图,并且我们创建的所有节点都将与该默认图关联。
会话
计算图只会被定义; 为了执行计算图,我们使用 TensorFlow 会话:
sess = tf.Session()
我们可以使用tf.Session()方法为我们的计算图创建会话,该方法将分配用于存储变量当前值的内存。 创建会话后,我们可以使用sess.run()方法执行图。
为了在 TensorFlow 中运行任何内容,我们需要为实例启动 TensorFlow 会话; 请参考代码:
import tensorflow as tf
a = tf.multiply(2,3)
print(a)
它将打印一个 TensorFlow 对象而不是6。 就像已经说过的,每当我们导入 TensorFlow 时,都会自动创建一个默认计算图,并且我们创建的所有节点a都将附加到该图上。 为了执行图,我们需要初始化一个 TensorFlow 会话,如下所示:
#Import tensorflow
import tensorflow as tf
#Initialize variables
a = tf.multiply(2,3)
#create tensorflow session for executing the session
with tf.Session() as sess:
#run the session
print(sess.run(a))
前面的代码将显示6。
TensorBoard
TensorBoard 是 TensorFlow 的可视化工具,可用于可视化计算图。 它也可以用来绘制各种定量指标和一些中间计算的结果。 使用 TensorBoard,我们可以轻松地可视化复杂的模型,这对于调试和共享非常有用。
现在,让我们构建一个基本的计算图,并在 TensorBoard 中对其进行可视化。
首先,让我们导入库:
import tensorflow as tf
接下来,我们初始化变量:
a = tf.constant(5)
b = tf.constant(4)
c = tf.multiply(a,b)
d = tf.constant(2)
e = tf.constant(3)
f = tf.multiply(d,e)
g = tf.add(c,f)
现在,我们将创建一个 TensorFlow 会话。 我们将使用tf.summary.FileWriter()将图的结果写入名为event的文件中:
with tf.Session() as sess:
writer = tf.summary.FileWriter("output", sess.graph)
print(sess.run(g))
writer.close()
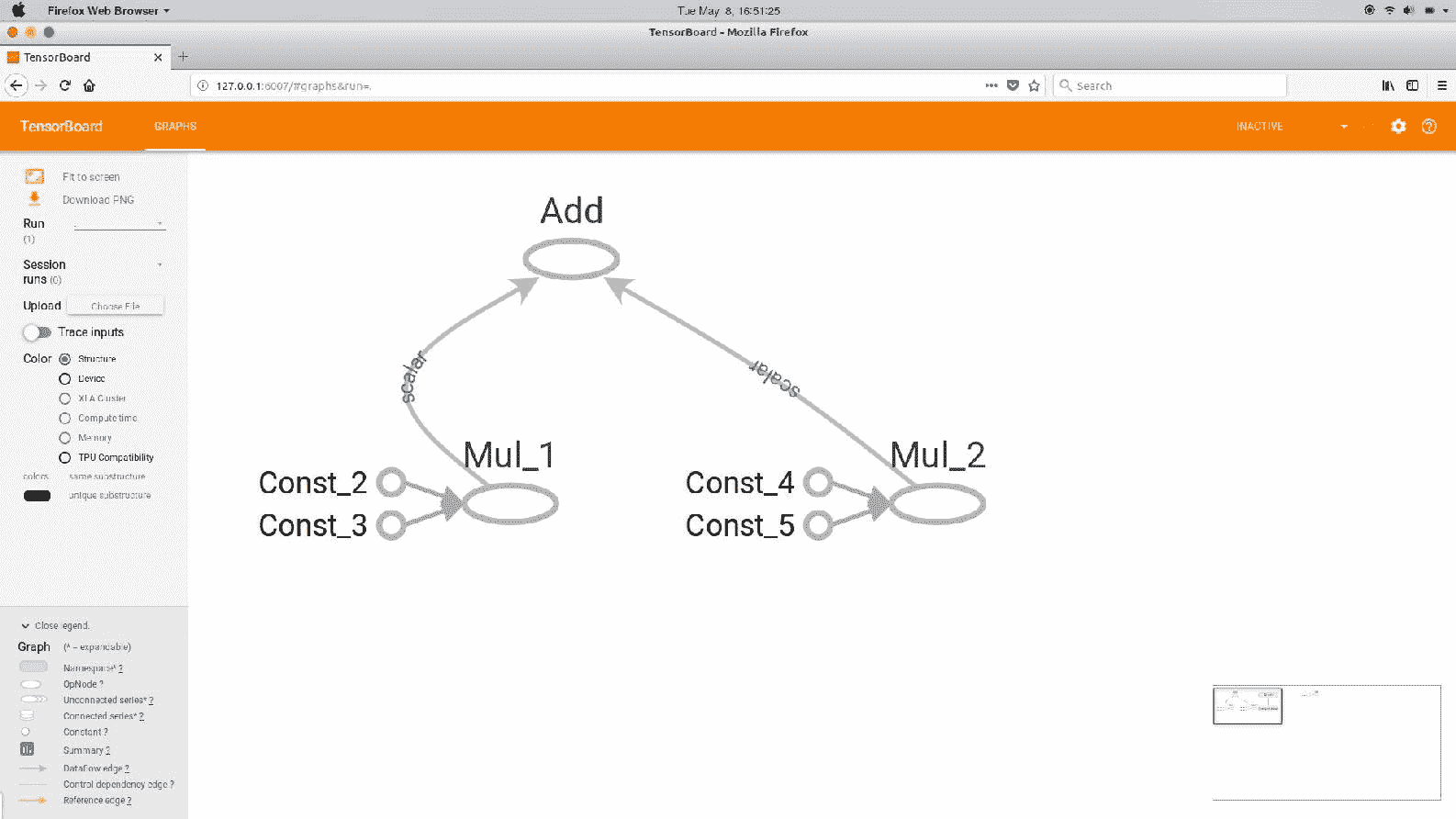
为了运行 TensorBoard,请转到您的终端,找到工作目录,然后键入tensorboard --logdir=output --port=6003。
您可以看到如下所示的输出:
添加范围
范围划分用于降低复杂性,并通过将相关节点分组在一起来帮助我们更好地理解模型。 例如,在前面的示例中,我们可以将图分为两个不同的组,称为计算和结果。 如果看前面的示例,可以看到节点a至e执行计算,而节点g计算结果。 因此,我们可以使用范围将它们分开分组,以便于理解。 可以使用tf.name_scope()函数创建作用域。
让我们通过Computation使用tf.name_scope()函数:
with tf.name_scope("Computation"):
a = tf.constant(5)
b = tf.constant(4)
c = tf.multiply(a,b)
d = tf.constant(2)
e = tf.constant(3)
f = tf.multiply(d,e)
让我们通过Result使用tf.name_scope()函数:
with tf.name_scope("Result"):
g = tf.add(c,f)
查看Computation范围; 我们可以将其进一步分解为更多的部分。 我们可以创建一个范围为Part 1并具有节点a至c的范围,并创建一个范围为Part 2并具有节点d至e的范围,因为第 1 部分和第 2 部分彼此独立 :
with tf.name_scope("Computation"):
with tf.name_scope("Part1"):
a = tf.constant(5)
b = tf.constant(4)
c = tf.multiply(a,b)
with tf.name_scope("Part2"):
d = tf.constant(2)
e = tf.constant(3)
f = tf.multiply(d,e)
通过在 TensorBoard 中可视化它们可以更好地了解作用域。 完整的代码如下:
import tensorflow as tf
with tf.name_scope("Computation"):
with tf.name_scope("Part1"):
a = tf.constant(5)
b = tf.constant(4)
c = tf.multiply(a,b)
with tf.name_scope("Part2"):
d = tf.constant(2)
e = tf.constant(3)
f = tf.multiply(d,e)
with tf.name_scope("Result"):
g = tf.add(c,f)
with tf.Session() as sess:
writer = tf.summary.FileWriter("output", sess.graph)
print(sess.run(g))
writer.close()
如果查看下图,您可以轻松地了解范围如何通过将相似节点分组在一起来帮助我们降低理解的复杂性。 范围界定在处理复杂项目时被广泛使用,以更好地了解节点的功能和依赖项:

总结
在本章中,我们学习了如何通过安装 Anaconda,Docker,OpenAI Gym,Universe 和 TensorFlow 来设置机器。 我们还学习了如何使用 OpenAI 创建模拟,以及如何训练智能体在 OpenAI 环境中学习。 然后,我们了解了 TensorFlow 的基础知识,然后在 TensorBoard 中可视化了图。
在下一章第 3 章,“马尔可夫决策过程和动态规划”中,我们将学习马尔可夫决策过程和动态规划以及如何使用值和策略迭代来解决冻湖问题。
问题
问题列表如下:
- 为什么以及如何在 Anaconda 中创建新环境?
- 使用 Docker 有什么需要?
- 我们如何在 OpenAI Gym 中模拟环境?
- 我们如何检查 OpenAI Gym 中的所有可用环境?
- OpenAI Gym 和 Universe 是否相同? 如果没有,原因是什么?
- TensorFlow 变量和占位符有何区别?
- 什么是计算图?
- 为什么我们需要 TensorFlow 中的会话?
- TensorBoard 的目的是什么?我们如何启动它?
进一步阅读
您可以进一步参考以下论文:
三、马尔可夫决策过程与动态规划
马尔可夫决策过程(MDP)提供了解决强化学习(RL)问题的数学框架。 几乎所有的 RL 问题都可以建模为 MDP。 MDP 被广泛用于解决各种优化问题。 在本章中,我们将了解什么是 MDP 以及如何使用它来解决 RL 问题。 我们还将学习动态规划,它是一种有效解决复杂问题的技术。
在本章中,您将学习以下主题:
- 马尔可夫链与马尔可夫过程
- 马尔可夫决策过程
- 奖励与回报
- 贝尔曼方程
- 使用动态规划求解贝尔曼方程
- 利用值和策略迭代来解决冻湖问题
马尔可夫链与马尔可夫过程
在进入 MDP 之前,让我们了解马尔可夫链和马尔可夫过程,它们构成了 MDP 的基础。
马尔可夫性质指出,未来仅取决于现在而不是过去。 马尔可夫链是一个概率模型,仅依靠当前状态来预测下一个状态,而不是先前的状态,也就是说,未来有条件地独立于过去。 马尔可夫链严格遵循马尔可夫属性。
例如,如果我们知道当前状态是多云,则可以预测下一个状态可能是雨天。 我们得出的结论是,只有考虑当前状态(多云)而不考虑过去的状态(可能是晴天,大风等),下一个状态才会下雨。 但是,马尔可夫属性并不适用于所有进程。 例如,掷骰子(下一个状态)与前一个数字无关,无论骰子上显示的是什么(当前状态)。
从一种状态移动到另一种状态称为转移,其概率称为转移概率。 我们可以用表格的形式来表示转移概率,如下所示,它被称为马尔可夫表。 在给定当前状态的情况下,它显示了移至下一个状态的概率为:
| 当前状态 | 下一个状态 | 转移概率 |
|---|---|---|
| 多云 | 下雨 | 0.6 |
| 下雨 | 下雨 | 0.2 |
| 晴天 | 多云 | 0.1 |
| 下雨 | 晴天 | 0.1 |
我们还可以以状态图的形式表示马尔可夫链,该状态图显示转移概率:

前面的状态图显示了从一种状态转移到另一种状态的可能性。 还是不了解马尔可夫链? 好吧,让我们谈谈。
我:“你在做什么?”
您:“我正在阅读有关马尔可夫链的信息。”
我:“看完书后你打算做什么?”
你:“我要睡觉了。”
我:“您确定要睡觉吗?”
您:“可能。如果我不困,我会看电视的。”
我:“很酷;这也是一条马尔可夫链。”
你:“嗯?”
我们可以将对话公式化为马尔可夫链,并绘制如下状态图:

马尔可夫链位于核心概念中,即未来仅取决于现在而不是过去。 如果遵循马尔可夫属性,则随机过程称为马尔可夫过程。
马尔可夫决策过程
MDP 是马尔可夫链的延伸。 它提供了用于建模决策情况的数学框架。 几乎所有的强化学习问题都可以建模为 MDP。
MDP 由五个重要元素表示:
- 智能体实际上可以处于的一组状态
(S)。 - 智能体可以执行的一组动作
(A),用于从一种状态转移到另一种状态。 - 转移概率(
P[ss']^a),是通过执行某些操作a从一种状态s转移到另一种状态s'的概率。 - 奖励概率(
R[ss']^a),是智能体通过执行某些动作a从一种状态s转移到另一种状态s'所获得的奖励的概率。 - 折扣因子(
γ),用于控制立即和将来奖励的重要性。 我们将在接下来的部分中详细讨论。
奖励与回报
如我们所知,在 RL 环境中,智能体通过执行操作与环境交互,并从一种状态转移到另一种状态。 根据其执行的动作,它会获得奖励。 奖励不过是一个数字值,例如,一个好动作为 +1,而一个坏动作为 -1。 我们如何确定一个动作是好是坏? 在迷宫游戏中,好动作是指智能体进行移动以使其不会撞到迷宫壁的地方,而不好的动作是指智能体进行移动并撞到迷宫壁的地方。
智能体试图最大化从环境而不是即时奖励中获得的奖励(累积奖励)总量。 智能体从环境中获得的总奖励金额称为回报。 因此,我们可以将智能体收到的奖励(回报)总额计算如下:

r[t + 1]是智能体在执行操作a[0]从一种状态转换到另一种状态时在时间步骤t[0]时收到的奖励。 r[t + 2]是智能体在执行从一个状态到另一状态的动作时,在
步骤t[1]时收到的奖励。 类似地,r[T]是智能体在执行从一个状态到另一状态的动作时,在最后时间步骤T所收到的奖励。
间歇性和连续性任务
情景任务是具有最终状态(结束)的任务。 在 RL 中,剧集被视为从初始状态到最终状态的智能体与环境的相互作用。
例如,在赛车视频游戏中,您启动游戏(初始状态)并玩游戏直到游戏结束(最终状态)。 这称为剧集。 游戏结束后,您可以通过重新启动游戏来开始下一个剧集,并且无论您在上一个游戏中所处的位置如何,都将从初始状态开始。 因此,每个剧集彼此独立。
在连续任务中,没有最终状态。 连续的任务永远不会结束。 例如,个人协助机器人没有最终状态。
折扣因子
我们已经看到,智能体的目标是使回报最大化。 对于一项临时任务,我们可以将返回定义为R[t] = r[t + 1] + r[t + 2] + ... + r[T],其中T是剧集的最终状态,我们尝试最大化回报R[t]。
由于连续任务没有任何最终状态,因此我们可以将连续任务的收益定义为R[t] = r[t + 1] + r[t + 2] + ...,总和为无穷大。 但是,如果永不止息,我们如何才能最大化回报呢?
这就是为什么我们引入折扣因子的概念。 我们可以使用折扣因子γ重新定义收益,如下所示:
 ---(1)
---(1)
 ---(2)
---(2)
折扣系数决定了我们对未来奖励和即时奖励的重视程度。 折扣因子的值在0至1之内。 折扣因子0意味着即时奖励更为重要,而折扣因子1意味着未来奖励比即时奖励更为重要。
折扣系数0永远不会只考虑立即获得的奖励。 同样,1的折扣因子将永远学习,以寻找未来的奖励,这可能导致无限。 因此,折扣因子的最佳值在 0.2 到 0.8 之间。
根据使用情况,我们重视即时奖励和将来的奖励。 在某些情况下,未来的奖励比立即的奖励更可取,反之亦然。 在国际象棋游戏中,目标是击败对手的国王。 如果我们重视即时奖励,而即时奖励是通过典当击败任何对手玩家等行动获得的,那么坐席将学会执行此子目标,而不是学习达到实际目标。 因此,在这种情况下,我们重视未来的奖励,而在某些情况下,我们更喜欢即时奖励,而不是未来的奖励。 (说,如果我今天或 13 个月后给您巧克力,您会喜欢巧克力吗?)
策略函数
我们已经在第 1 章,“强化学习简介”中了解了策略函数,该函数将状态映射到操作。 用π表示。
策略函数可以表示为π(s): s -> a,指示从状态到动作的映射。 因此,基本上,策略函数会说明在每种状态下要执行的操作。 我们的最终目标在于找到最佳策略,该策略指定在每个状态下执行的正确操作,从而最大化回报。
状态值函数
状态值函数也简称为值函数。 它通过策略π指定智能体处于特定状态的状态如何。 值函数通常由V(s)表示。 它表示遵循策略的状态的值。
我们可以定义一个状态值函数,如下所示:
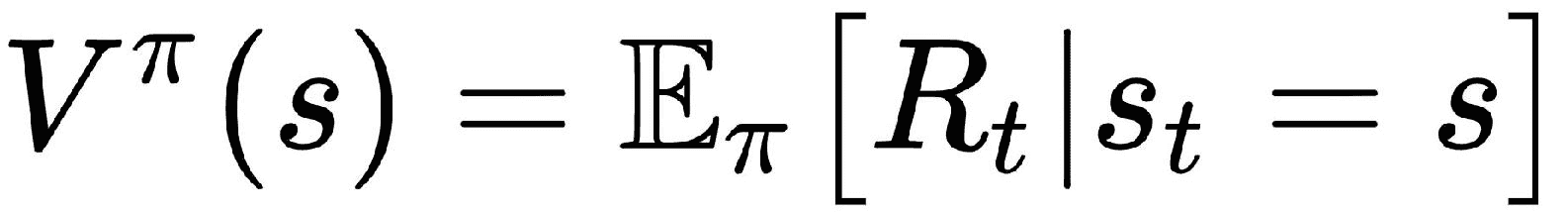
这根据策略π指定从状态s开始的预期收益。 我们可以用(2)的值函数替换R[t]的值,如下所示:

请注意,状态值函数取决于策略,并且取决于我们选择的策略而有所不同。
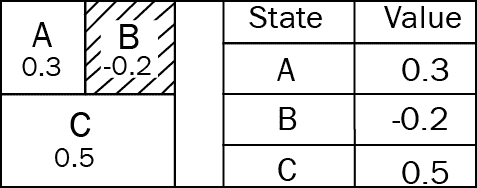
我们可以在表中查看值函数。 假设我们有两个状态,并且这两个状态都遵循策略π。 根据这两个状态的值,我们可以判断出执行策略后,我们的智能体处于该状态有多好。 值越大,状态越好:
| 状态 | 值 |
|---|---|
| 状态 1 | 0.3 |
| 状态 2 | 0.9 |
根据上表,我们可以知道处于状态 2 很好,因为它具有很高的值。 在接下来的部分中,我们将看到如何直观地估计这些值。
状态作用值函数(Q 函数)
状态作用值函数也称为Q函数。 它指定智能体在具有策略π的状态下执行特定操作的效果如何。Q函数由Q(s)表示。 它表示在遵循策略π的状态下执行操作的值。
我们可以定义Q函数,如下所示:

这根据策略π指定从状态s开始的预期回报,其动作为a。 我们可以从(2)的Q函数中替换R[t]的值,如下所示:

值函数和Q函数之间的区别在于,值函数指定状态的优劣,而Q函数指定状态的行为的优劣。
与状态值函数一样,Q函数可以在表中查看。 也称为Q表。 让我们说我们有两个状态和两个动作。 我们的Q表如下所示:
| 状态 | 动作 | 值 |
|---|---|---|
| 状态 1 | 动作 1 | 0.03 |
| 状态 1 | 动作 2 | 0.02 |
| 状态 2 | 动作 1 | 0.5 |
| 状态 2 | 动作 2 | 0.9 |
因此,Q表显示了所有可能的状态动作对的值。 因此,通过查看此表,我们可以得出结论,在状态 1 中执行动作 1 和在状态 2 中执行动作 2 是更好的选择,因为它具有很高的值。
每当我们说值函数V(S)或Q函数Q(S, a)时,它实际上表示值表,而Q表,如前所示。
贝尔曼方程和最优性
以美国数学家理查德·贝尔曼(Richard Bellman)命名的贝尔曼方程式可帮助我们求解 MDP。 它在 RL 中无处不在。 当我们说解决 MDP 时,实际上意味着找到最佳的策略和值函数。 根据不同的策略,可以有许多不同的值函数。 与所有其他值函数相比,最优值函数V*(s)是产生最大值的函数:

类似地,最优策略是导致最优值函数的策略。
由于最优值函数V*(s)是比所有其他值函数(即最大收益)更高的值的函数,因此它将是Q函数的最大值。 因此,可以通过将Q函数的最大值取如下来轻松地计算最佳值函数:
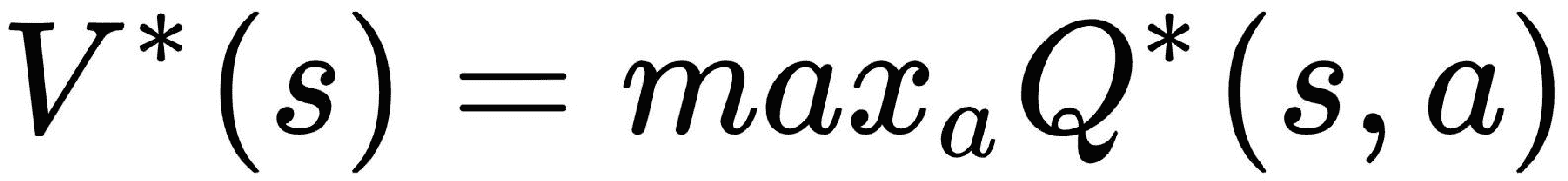 ---(3)
---(3)
值函数的贝尔曼方程可以表示为(在下一主题中,我们将看到如何推导该方程):
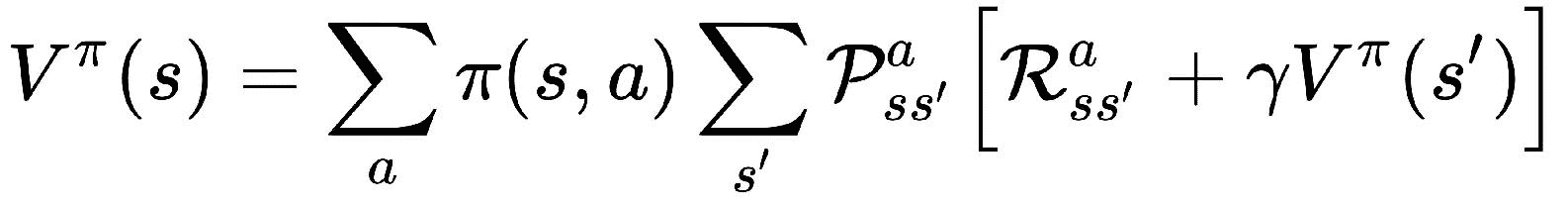
它指示状态值及其后继状态与所有可能性的平均值之间的递归关系。
类似地,用于Q函数的贝尔曼方程可以表示为:
 ---(4)
---(4)
将公式(4)代入(3),我们得到:
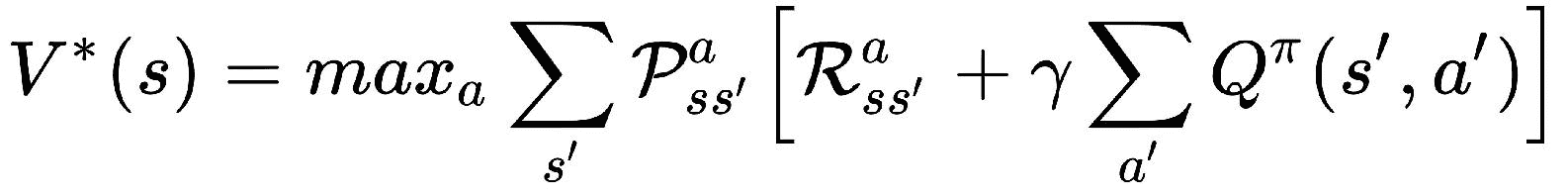
前面的方程式称为贝尔曼最优方程式。 在接下来的部分中,我们将看到如何通过求解该方程式找到最佳策略。
推导值和 Q 函数的贝尔曼方程
现在,让我们看看如何导出值和Q函数的贝尔曼方程。
如果您对数学不感兴趣,可以跳过本节。 但是,数学将非常有趣。
首先,我们将P[ss']^a定义为在执行动作a时从状态s转换为s'的转移概率:

我们将R[ss']^a定义为在执行动作a时从状态s移至s'所获得的奖励概率:
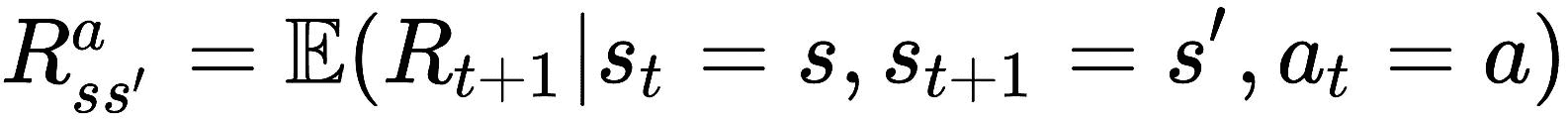
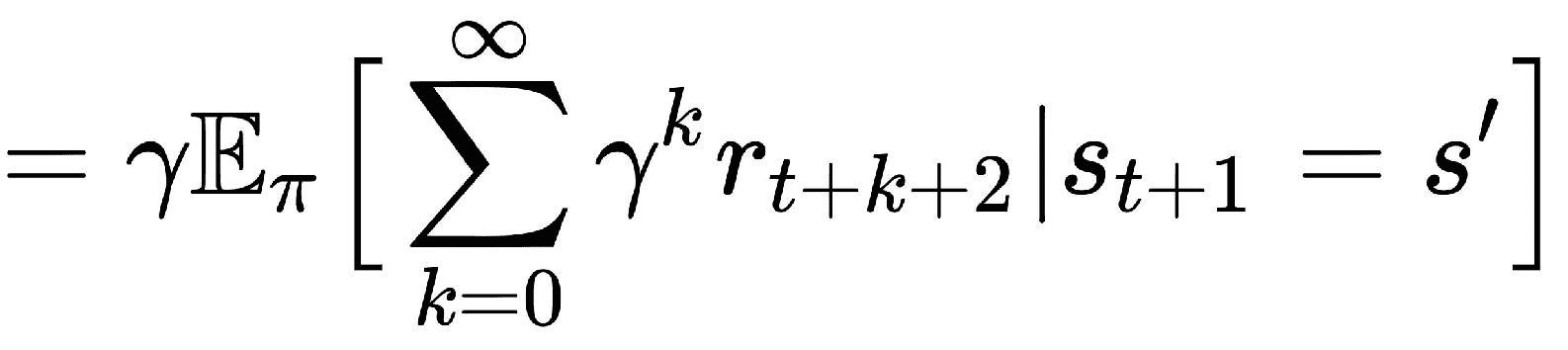 来自(2)---(5)
来自(2)---(5)
我们知道值函数可以表示为:
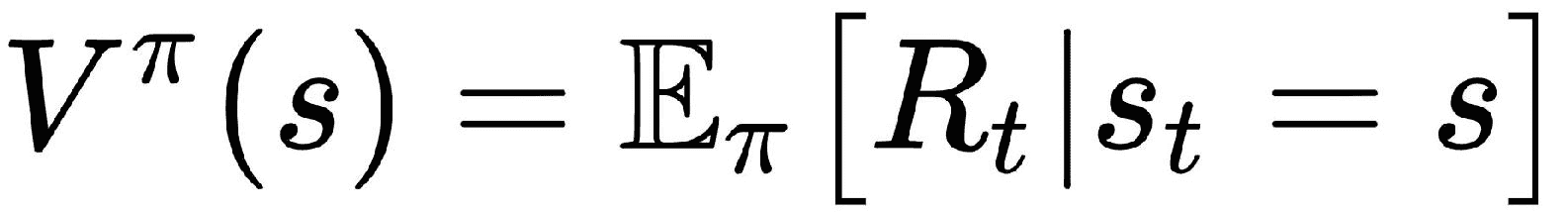
 来自(1)
来自(1)
我们可以通过获取第一笔报酬来重写值函数:
 ---(6)
---(6)
如果我们处于状态s,并通过策略π执行动作a,则值函数中的期望值指定了期望收益。
因此,我们可以通过总结所有可能的动作和奖励来明确地重写我们的期望,如下所示:
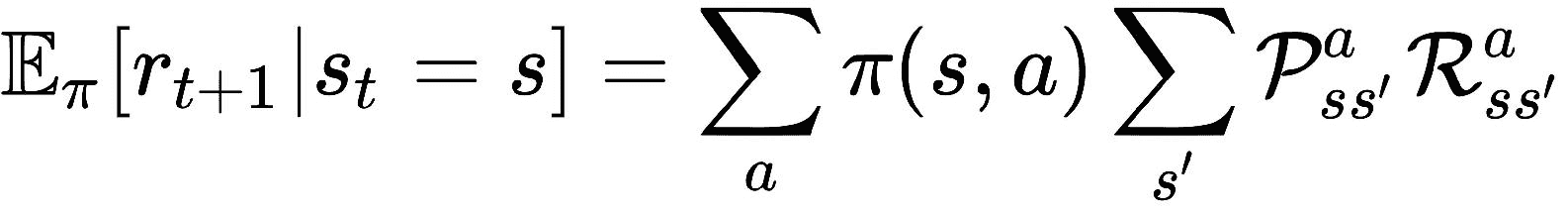
在 RHS 中,我们将等式(5)中的R[ss']^a替换为:

同样,在 LHS 中,我们将从等式(2)中替换r[t + 1]的值,如下所示:

因此,我们的最终期望方程变为:
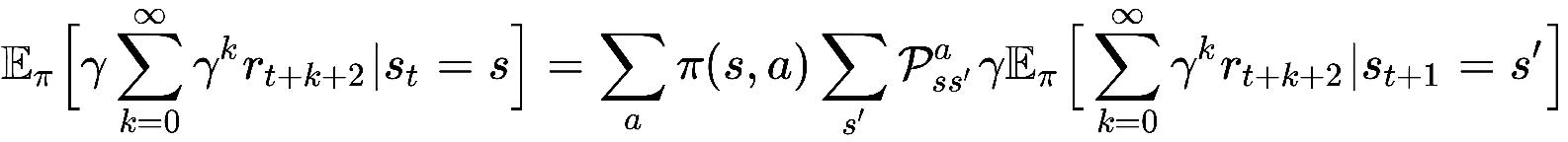 ---(7)
---(7)
现在,我们将期望值(7)替换为值函数(6),如下所示:
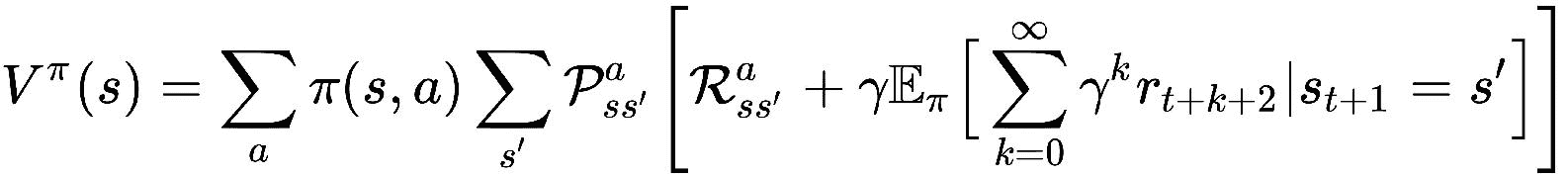
代替

我们可以用等式(6)代替V[s']^π,我们的最终值函数如下所示:

以非常相似的方式,我们可以为Q函数导出一个贝尔曼方程; 最终方程如下:

现在,对于值函数和Q函数都有一个贝尔曼方程,我们将看到如何找到最佳策略。
求解贝尔曼方程
我们可以通过求解贝尔曼最优性方程来找到最优策略。 为了解决贝尔曼最优性方程,我们使用一种称为动态规划的特殊技术。
动态规划
动态规划(DP)是一种解决复杂问题的技术。 在 DP 中,不是一次解决一个复杂的问题,而是将问题分解为简单的子问题,然后针对每个子问题,我们计算并存储解决方案。 如果出现相同的子问题,我们将不会重新计算,而是使用已经计算的解决方案。 因此,DP 有助于极大地减少计算时间。 它的应用广泛,包括计算机科学,数学,生物信息学等。
我们使用两种强大的算法来求解贝尔曼方程:
- 值迭代
- 策略迭代
值迭代
在值迭代中,我们从随机值函数开始。 显然,随机值函数可能不是最佳函数,因此我们以迭代方式寻找新的改进值函数,直到找到最佳值函数为止。 一旦找到最优值函数,就可以轻松地从中得出最优策略:

值迭代涉及的步骤如下:
- 首先,我们初始化随机值函数,即每个状态的随机值。
- 然后,我们为
Q(s, a)的所有状态动作对计算Q函数。 - 然后,我们使用
Q(s, a)中的最大值更新值函数。 - 我们重复这些步骤,直到值函数的变化很小。
让我们通过手动逐步执行值迭代来直观地理解它。
考虑此处显示的网格。 让我们说我们处于状态A,我们的目标是在不访问状态B的情况下达到状态C,我们有两个动作,0 是左/右和 1 是上/下:
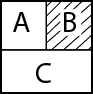
您能想到这里的最佳策略吗? 此处的最佳策略是告诉我们在A状态下执行操作 1 的策略,这样我们就可以访问C而无需访问B。 我们如何找到这个最佳策略? 现在让我们看看:
初始化随机值函数,即所有状态的随机值。 让我们将0分配给所有状态:

让我们计算所有状态动作对的Q值。
Q 值告诉我们每个状态下一个动作的值。 首先,让我们计算状态A的Q值。 调用Q函数的方程式。 为了进行计算,我们需要转移和奖励概率。 让我们考虑状态A的转移和奖励概率,如下所示:

状态A的 Q 函数可以计算如下:
Q(s, a) = 转移概率 * (奖励概率 + gamma * next_state 的值)
在此,gamma是折扣因子; 我们将其视为1。
状态A和操作0的 Q 值:

Q(A, 0) = (0.1 * (0 + 0)) + (0.4 * (-1.0 + 0)) + (0.3 * (1.0 + 0))
Q(A, 0) = -0.1
现在我们将计算状态A和操作1的Q值:

Q(A, 1) = (0.3 * (0 + 0)) + (0.1 * (-2.0 + 0)) + (0.5 * (1.0 + 0))
Q(A, 1) = 0.3
现在,我们将在Q表中对此进行更新,如下所示:
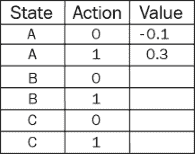
从Q(s, a)更新值函数为最大值。
如果您查看前面的Q函数,则Q(A, 1)的值大于Q(A, 0)的值,因此我们将将状态A的值更新为Q(A, 1):
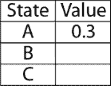
同样,我们为所有状态动作对计算Q值,并通过获取具有最高状态动作值的Q值来更新每个状态的值函数。 我们的更新值函数如下所示。 这是第一次迭代的结果:
我们重复此步骤几次迭代。 也就是说,我们将步骤2重复到步骤3(在每次迭代中,在计算Q值时,我们使用更新后的值函数,而不是相同的随机初始化函数) 值函数)。
这是第二次迭代的结果:

这是第三次迭代的结果:
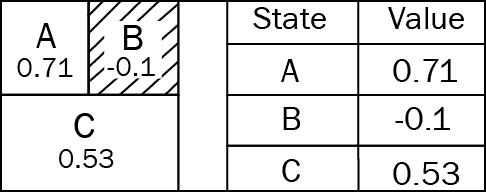
但是我们什么时候停止呢? 当每次迭代之间的值变化较小时,我们将停止; 如果查看第二和第三次迭代,则值函数的变化不大。 在这种情况下,我们停止迭代并将其视为最佳值函数。
好了,既然我们已经找到了最优值函数,那么我们如何得出最优策略呢?
这很简单。 我们用最终的最优值函数计算Q函数。 假设我们计算出的Q函数如下所示:

从此Q函数中,我们选择每种状态下具有最大值的动作。 在状态A下,我们为操作 1 设置了最大值,这是我们的最佳策略。 因此,如果我们在状态A中执行动作 1,则无需访问B就可以达到C。
策略迭代
与值迭代不同,在策略迭代中,我们从随机策略开始,然后找到该策略的值函数。 如果值函数不是最优的,那么我们会找到新的改进策略。 我们重复此过程,直到找到最佳策略。
策略迭代有两个步骤:
- 策略评估:评估随机估计策略的值函数。
- 策略改进:在评估值函数时,如果它不是最优的,我们会发现新的改进策略:
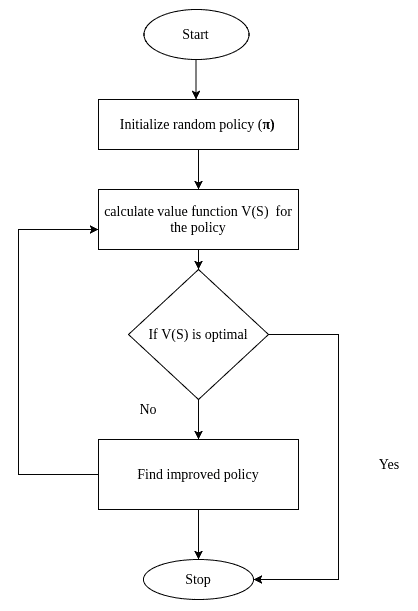
策略迭代涉及的步骤如下:
- 首先,我们初始化一些随机策略
- 然后我们找到该随机策略的值函数,并进行评估以检查其是否最优,这称为策略评估
- 如果不是最佳选择,我们会找到新的改进策略,称为策略改进
- 我们重复这些步骤,直到找到最佳策略
让我们通过逐步手动执行策略迭代来直观地理解。
考虑我们在值迭代部分中看到的相同网格示例。 我们的目标是找到最佳策略:
- 初始化随机策略函数。
让我们通过为每个状态指定随机动作来初始化随机策略函数:
A -> 0
B -> 1
C -> 0
- 查找随机初始化策略的值函数。
现在,我们必须使用随机初始化的策略来查找值函数。 我们说一下计算后的值函数如下:

现在,根据随机初始化的策略有了新的值函数,让我们使用新的值函数计算新的策略。 我们如何做到这一点? 这与我们在值迭代中所做的非常相似。 我们为新值函数计算Q值,然后针对具有最大值的每个状态采取措施作为新策略。
我们说新策略的结果是:
A -> 0
B -> 1
C -> 1
我们检查旧策略,即随机初始化的策略和新策略。 如果它们相同,则我们已经达到收敛,即找到了最佳策略。 如果没有,我们将旧策略(随机策略)更新为新策略,并从步骤2开始重复。
听起来令人困惑? 看一下伪代码:
policy_iteration():
Initialize random policy
for i in no_of_iterations:
Q_value = value_function(random_policy)
new_policy = Maximum state action pair from Q value
if random_policy == new policy:
break
random_policy = new_policy
return policy
解决冻湖问题
如果您到目前为止还不了解我们所学的知识,请放心,我们将研究所有概念以及冻湖问题。
想象一下,有一个从家到办公室的冰冻湖泊。 您必须在结冰的湖面上行走才能到达办公室。 但是糟糕! 冰冻的湖面上有洞,因此您在冰冻的湖面上行走时必须小心,以免被困在洞中:

看上图:
S是起始位置(原点)F是您可以漫步的冰冻湖H是孔,您必须非常小心G是目标(办公室)
好的,现在让我们代替您使用我们的智能体来找到到达办公室的正确方法。 该智能体的目标是找到从S到G的最佳路径,而不会陷入H的陷阱。 智能体如何做到这一点? 如果智能体正确地在冰冻的湖面上行走,我们给 +1 分作为奖励,如果智能体正确落入洞中,则给 0 分,以便智能体确定正确的行动。 智能体现在将尝试找到最佳策略。 最优策略意味着采取正确的道路,这将最大化智能体的报酬。 如果智能体正在使报酬最大化,则显然智能体正在学习跳过漏洞并到达目的地。
我们可以将问题建模为我们先前研究的 MDP。 MDP 包含以下内容:
- 状态:状态集。 在这里,我们有 16 个状态(网格中的每个小方框)。
- 动作:所有可能动作的集合(左,右,上,下;这是我们的智能体在冰冻湖面环境中可以采取的所有四种可能动作)。
- 转移概率:通过执行动作
a从一种状态(F)转换为另一种状态(H)的概率。 - 奖励概率:这是执行动作
a从一种状态(F)迁移到另一种状态(H)时获得奖励的概率。
现在我们的目标是解决 MDP。 解决 MDP 意味着寻找最佳策略。 现在,我们介绍三个特殊函数:
- 策略函数:指定在每种状态下要执行的操作
- 值函数:指定状态的良好程度
- Q 函数:指定动作在特定状态下的状态
当我们说有多好时,这到底意味着什么? 这意味着最大化奖励是多么的好。
然后,我们使用称为贝尔曼最优性方程的特殊方程式表示值函数和Q函数。 如果我们解决这个方程,我们可以找到最佳策略。 在这里,求解方程式意味着找到正确的值函数和策略。 如果我们找到正确的值函数和策略,那将是我们获得最大回报的最佳途径。
我们将使用一种称为动态规划的特殊技术来求解贝尔曼最优性方程。 要应用 DP,必须预先知道模型动态,这基本上意味着必须预先知道模型环境的转换概率和奖励概率。 由于我们知道模型动态,因此可以在此处使用 DP。 我们使用两种特殊的 DP 算法来找到最佳策略:
- 值迭代
- 策略迭代
值迭代
简单来说,在值迭代中,我们首先将一些随机值初始化为值函数。 我们初始化的随机值很有可能不会达到最佳状态。 因此,我们遍历每个状态并找到新的值函数; 我们停止迭代,直到找到最佳值函数。 一旦找到最优值函数,就可以轻松地从中提取最优策略。
现在我们将看到如何使用值迭代来解决冻湖问题。
首先,我们导入必要的库:
import gym
import numpy as np
然后,我们使用 OpenAI 的 Gym 创建冰冻的湖泊环境:
env = gym.make('FrozenLake-v0')
我们将首先探索环境。
由于我们有一个4 * 4的网格,因此环境中的状态数为 16:
print(env.observation_space.n)
环境中的操作数为四个,分别为上,下,左和右:
print(env.observation_space.n)
现在我们定义一个value_iteration()函数,该函数返回最佳值函数(值表)。 我们将首先逐步了解该函数,然后再查看整个函数。
首先,我们为所有状态和迭代次数初始化随机值表0:
value_table = np.zeros(env.observation_space.n)
no_of_iterations = 100000
然后,在每次迭代开始时,我们将value_table复制到updated_value_table:
for i in range(no_of_iterations):
updated_value_table = np.copy(value_table)
现在,我们计算 Q 表,并选择具有最高值的最大状态动作对作为值表。
我们将使用之前解决的示例来理解代码。 我们在上一个示例中计算了状态A和操作1的Q值:
Q(A, 1) = (0.3 * (0 + 0)) + (0.1 * (-1.0 + 0)) + (0.5 + (1.0 + 0))
Q(A, 1) = 0.5
我们没有为每个状态创建Q表,而是创建了一个名为Q_value的列表,然后为该状态中的每个动作创建了一个名为next_states_rewards的列表,该列表存储了Q_value 下一个转移状态。 然后,我们对next_state_rewards求和并将其附加到我们的Q_value中。
请看前面的示例,其中状态为A,操作为1。 (0.3 * (0 + 0))是转移状态A的下一个状态奖励,(0.1 * (-1.0 + 0))是转移状态B的下一状态奖励。 (0.5 + (1.0 + 0))是转移状态C的下一个状态奖励。 我们将所有这些加总为next_state_reward,并将其附加到Q_value中,该值为 0.5。
当我们为状态的所有动作计算next_state_rewards并将其附加到Q值时,我们选取最大的Q值并将其更新为我们的状态值:
for state in range(env.observation_space.n):
Q_value = []
for action in range(env.action_space.n):
next_states_rewards = []
for next_sr in env.P[state][action]:
trans_prob, next_state, reward_prob, _ = next_sr
next_states_rewards.append((trans_prob * (reward_prob + gamma * updated_value_table[next_state])))
Q_value.append(np.sum(next_states_rewards))
#Pick up the maximum Q value and update it as value of a state
value_table[state] = max(Q_value)
然后,我们将检查是否已经达到收敛,即,我们的值表和更新后的值表之间的差异非常小。 我们怎么知道它很小? 我们定义了一个名为threshold的变量,然后我们看一下差异是否小于我们的threshold; 如果小于,则中断循环,并将值函数返回为最佳值函数:
threshold = 1e-20
if (np.sum(np.fabs(updated_value_table - value_table)) <= threshold):
print ('Value-iteration converged at iteration# %d.' %(i+1))
break
查看value_iteration()的完整函数可以更好地理解:
def value_iteration(env, gamma = 1.0):
value_table = np.zeros(env.observation_space.n)
no_of_iterations = 100000
threshold = 1e-20
for i in range(no_of_iterations):
updated_value_table = np.copy(value_table)
for state in range(env.observation_space.n):
Q_value = []
for action in range(env.action_space.n):
next_states_rewards = []
for next_sr in env.P[state][action]:
trans_prob, next_state, reward_prob, _ = next_sr
next_states_rewards.append((trans_prob * (reward_prob + gamma * updated_value_table[next_state])))
Q_value.append(np.sum(next_states_rewards))
value_table[state] = max(Q_value)
if (np.sum(np.fabs(updated_value_table - value_table)) <= threshold):
print ('Value-iteration converged at iteration# %d.' %(i+1))
break
return value_table, Q_value
因此,我们可以使用value_iteration导出optimal_value_function:
optimal_value_function = value_iteration(env=env,gamma=1.0)
找到optimal_value_function后,如何从optimal_value_function中提取最佳策略? 我们使用最佳值操作来计算Q值,并选择每个状态中具有最高Q值的操作作为最佳策略。 我们通过称为extract_policy()的函数来完成此操作; 我们现在将逐步介绍这一点。
首先,我们定义随机策略; 对于所有状态,我们将其定义为0:
policy = np.zeros(env.observation_space.n)
然后,对于每个状态,我们都构建一个Q_table,并且针对该状态中的每个动作,我们计算Q值并将其添加到我们的Q_table中:
for state in range(env.observation_space.n):
Q_table = np.zeros(env.action_space.n)
for action in range(env.action_space.n):
for next_sr in env.P[state][action]:
trans_prob, next_state, reward_prob, _ = next_sr
Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
然后,我们为state选择策略,将其作为具有Q最高值的操作:
policy[state] = np.argmax(Q_table)
看一下完整的函数:
def extract_policy(value_table, gamma = 1.0):
policy = np.zeros(env.observation_space.n)
for state in range(env.observation_space.n):
Q_table = np.zeros(env.action_space.n)
for action in range(env.action_space.n):
for next_sr in env.P[state][action]:
trans_prob, next_state, reward_prob, _ = next_sr
Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
policy[state] = np.argmax(Q_table)
return policy
因此,我们可以得出optimal_policy如下:
optimal_policy = extract_policy(optimal_value_function, gamma=1.0)
我们将获得如下输出,即optimal_policy,即在每种状态下要执行的操作:
array([0., 3., 3., 3., 0., 0., 0., 0., 3., 1., 0., 0., 0., 2., 1., 0.])
完整的程序如下:
import gym
import numpy as np
env = gym.make('FrozenLake-v0')
def value_iteration(env, gamma = 1.0):
value_table = np.zeros(env.observation_space.n)
no_of_iterations = 100000
threshold = 1e-20
for i in range(no_of_iterations):
updated_value_table = np.copy(value_table)
for state in range(env.observation_space.n):
Q_value = []
for action in range(env.action_space.n):
next_states_rewards = []
for next_sr in env.P[state][action]:
trans_prob, next_state, reward_prob, _ = next_sr
next_states_rewards.append((trans_prob * (reward_prob + gamma * updated_value_table[next_state])))
Q_value.append(np.sum(next_states_rewards))
value_table[state] = max(Q_value)
if (np.sum(np.fabs(updated_value_table - value_table)) <= threshold):
print ('Value-iteration converged at iteration# %d.' %(i+1))
break
return value_table
def extract_policy(value_table, gamma = 1.0):
policy = np.zeros(env.observation_space.n)
for state in range(env.observation_space.n):
Q_table = np.zeros(env.action_space.n)
for action in range(env.action_space.n):
for next_sr in env.P[state][action]:
trans_prob, next_state, reward_prob, _ = next_sr
Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
policy[state] = np.argmax(Q_table)
return policy
optimal_value_function = value_iteration(env=env,gamma=1.0)
optimal_policy = extract_policy(optimal_value_function, gamma=1.0)
print(optimal_policy)
策略迭代
在策略迭代中,首先我们初始化一个随机策略。 然后,我们将评估初始化的随机策略:它们是否好? 但是,我们如何评估策略呢? 我们将通过计算它们的值函数来评估我们随机初始化的策略。 如果它们不好,那么我们会找到新的策略。 我们重复此过程,直到找到好的策略。
现在让我们看看如何使用策略迭代来解决冻湖问题。
在查看策略迭代之前,我们将了解在给定策略的情况下如何计算值函数。
我们用状态数将value_table初始化为零:
value_table = np.zeros(env.nS)
然后,对于每个状态,我们从策略中获取操作,然后根据action和state计算值函数,如下所示:
updated_value_table = np.copy(value_table)
for state in range(env.nS):
action = policy[state]
value_table[state] = sum([trans_prob * (reward_prob + gamma * updated_value_table[next_state])
for trans_prob, next_state, reward_prob, _ in env.P[state][action]])
当value_table和updated_value_table之差小于我们的threshold时,我们将打破这一点:
threshold = 1e-10
if (np.sum((np.fabs(updated_value_table - value_table))) <= threshold):
break
查看以下完整函数:
def compute_value_function(policy, gamma=1.0):
value_table = np.zeros(env.nS)
threshold = 1e-10
while True:
updated_value_table = np.copy(value_table)
for state in range(env.nS):
action = policy[state]
value_table[state] = sum([trans_prob * (reward_prob + gamma * updated_value_table[next_state])
for trans_prob, next_state, reward_prob, _ in env.P[state][action]])
if (np.sum((np.fabs(updated_value_table - value_table))) <= threshold):
break
return value_table
现在,我们将逐步了解如何执行策略迭代。
首先,我们将random_policy初始化为零个 NumPy 数组,其形状为状态数:
random_policy = np.zeros(env.observation_space.n)
然后,对于每次迭代,我们根据随机策略计算new_value_function:
new_value_function = compute_value_function(random_policy, gamma)
我们将使用计算出的new_value_function提取策略。 extract_policy函数与我们在值迭代中使用的函数相同:
new_policy = extract_policy(new_value_function, gamma)
然后,我们检查是否已经达到收敛,即是否通过比较random_policy和新策略找到了最佳策略。 如果它们相同,我们将中断迭代。 否则,我们用new_policy更新random_policy:
if (np.all(random_policy == new_policy)):
print ('Policy-Iteration converged at step %d.' %(i+1))
break
random_policy = new_policy
查看完整的policy_iteration函数:
def policy_iteration(env,gamma = 1.0):
random_policy = np.zeros(env.observation_space.n)
no_of_iterations = 200000
gamma = 1.0
for i in range(no_of_iterations):
new_value_function = compute_value_function(random_policy, gamma)
new_policy = extract_policy(new_value_function, gamma)
if (np.all(random_policy == new_policy)):
print ('Policy-Iteration converged at step %d.' %(i+1))
break
random_policy = new_policy
return new_policy
因此,我们可以使用policy_iteration获得optimal_policy:
optimal_policy = policy_iteration(env, gamma = 1.0)
我们将获得一些输出,即optimal_policy,这是在每种状态下要执行的操作:
array([0., 3., 3., 3., 0., 0., 0., 0., 3., 1., 0., 0., 0., 2., 1., 0.])
完整的程序如下:
import gym
import numpy as np
env = gym.make('FrozenLake-v0')
def compute_value_function(policy, gamma=1.0):
value_table = np.zeros(env.nS)
threshold = 1e-10
while True:
updated_value_table = np.copy(value_table)
for state in range(env.nS):
action = policy[state]
value_table[state] = sum([trans_prob * (reward_prob + gamma * updated_value_table[next_state])
for trans_prob, next_state, reward_prob, _ in env.P[state][action]])
if (np.sum((np.fabs(updated_value_table - value_table))) <= threshold):
break
return value_table
def extract_policy(value_table, gamma = 1.0):
policy = np.zeros(env.observation_space.n)
for state in range(env.observation_space.n):
Q_table = np.zeros(env.action_space.n)
for action in range(env.action_space.n):
for next_sr in env.P[state][action]:
trans_prob, next_state, reward_prob, _ = next_sr
Q_table[action] += (trans_prob * (reward_prob + gamma * value_table[next_state]))
policy[state] = np.argmax(Q_table)
return policy
def policy_iteration(env,gamma = 1.0):
random_policy = np.zeros(env.observation_space.n)
no_of_iterations = 200000
gamma = 1.0
for i in range(no_of_iterations):
new_value_function = compute_value_function(random_policy, gamma)
new_policy = extract_policy(new_value_function, gamma)
if (np.all(random_policy == new_policy)):
print ('Policy-Iteration converged at step %d.' %(i+1))
break
random_policy = new_policy
return new_policy
print (policy_iteration(env))
因此,我们可以得出最佳策略,该策略使用值和策略迭代来解决冻结湖问题,从而指定在每种状态下要执行的操作。
总结
在本章中,我们了解了什么是马尔可夫链和马尔可夫过程,以及如何使用 MDP 表示 RL 问题。 我们还研究了贝尔曼方程,并解决了贝尔曼方程,从而使用 DP 推导了最优策略。 在下一章第 4 章,“使用蒙特卡洛方法进行游戏”中,我们将研究蒙特卡洛树搜索以及如何使用它进行智能游戏的构建。
问题
问题列表如下:
- 马尔可夫属性是什么?
- 为什么我们需要马尔可夫决策过程?
- 我们何时更喜欢即时奖励?
- 折扣因子有什么用?
- 为什么要使用贝尔曼函数?
- 您将如何导出 Q 函数的贝尔曼方程?
- 值函数和 Q 函数有何关系?
- 值迭代和策略迭代有什么区别?
进一步阅读
四、用于游戏的蒙特卡洛方法
蒙特卡洛算法是从物理,机械到计算机科学的各个领域中最受欢迎和最常用的算法之一。 当未知环境模型时,在强化学习(RL)中使用蒙特卡洛算法。 在上一章第 3 章,“马尔可夫决策过程和动态规划”中,我们着眼于使用动态规划(DP)查找我们了解模型动态的最佳策略,即转移和奖励概率。 但是,当我们不知道模型动态时,如何确定最佳策略? 在这种情况下,我们使用蒙特卡洛算法; 当我们不了解环境时,它对于找到最佳策略非常有用。
在本章中,您将了解以下内容:
- 蒙特卡洛方法
- 蒙特卡洛预测
- 使用蒙特卡洛玩二十一点
- 蒙特卡洛控制模型
- 蒙特卡洛探索
- 策略性蒙特卡洛控制
- 脱离策略的蒙特卡洛控制
蒙特卡洛方法
蒙特卡洛方法通过随机采样找到近似解,也就是说,它通过运行多个踪迹来近似结果的概率。 通过抽样找到近似答案是一种统计技术。 让我们通过一个示例更好地直观地了解蒙特卡洛。
有趣的事实:蒙特卡洛以斯坦尼斯瓦夫·乌兰的叔叔的名字命名,他经常从亲戚那里借钱在蒙特卡洛赌场赌博。
使用蒙特卡洛估计pi的值
想象一下,将一个圆的象限放置在正方形内,如下所示,然后我们在正方形内生成一些随机点。 您会看到一些点落在圆内,而另一些点在圆外:

我们可以这样写:

我们知道一个圆的面积是πr^2,一个正方形的面积是a^2:

让我们考虑一个圆的半径是一半,而正方形的边是1,因此我们可以替换为:
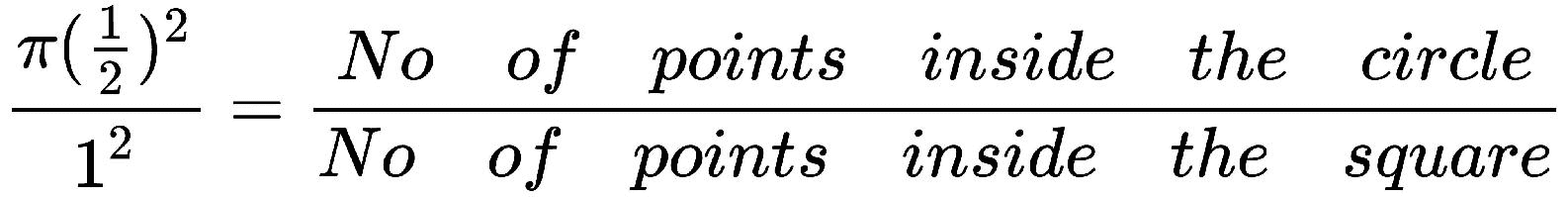
现在我们得到以下内容:
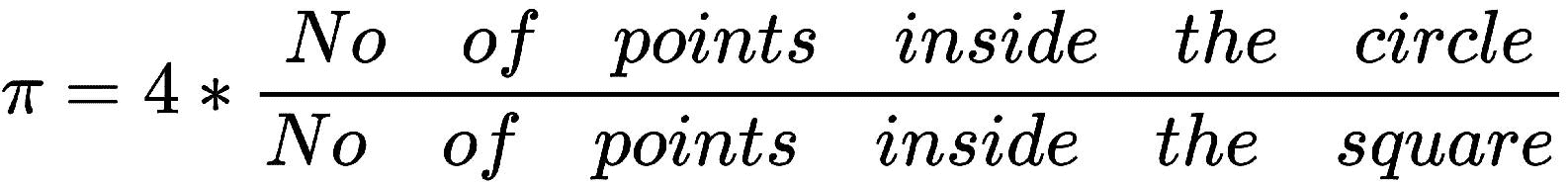
估计π的步骤非常简单:
- 首先,我们在正方形内生成一些随机点。
- 然后,我们可以使用公式
x^2 + y^2 <= size计算落入圆内的点数。 - 然后,我们通过将圆内的点数除以平方内的点数的四倍来计算π的值。
- 如果我们增加样本数(随机点数),则可以更好地近似
让我们逐步了解如何在 Python 中执行此操作。 首先,我们导入必要的库:
import numpy as np
import math
import random
import matplotlib.pyplot as plt
%matplotlib inline
现在,我们初始化圆和正方形内的正方形大小和点数。 我们还初始化了样本大小,该样本大小表示要生成的随机点数。 我们定义arc,它基本上是圆象限:
square_size = 1
points_inside_circle = 0
points_inside_square = 0
sample_size = 1000
arc = np.linspace(0, np.pi/2, 100)
然后,我们定义一个名为generate_points()的函数,该函数在正方形内部生成随机点:
def generate_points(size):
x = random.random()*size
y = random.random()*size
return (x, y)
我们定义了一个名为is_in_circle()的函数,该函数将检查生成的点是否在圆内:
def is_in_circle(point, size):
return math.sqrt(point[0]**2 + point[1]**2) <= size
然后定义一个用于计算π值的函数:
def compute_pi(points_inside_circle, points_inside_square):
return 4 * (points_inside_circle / points_inside_square)
然后对于样本数,我们在正方形内生成一些随机点,并增加points_inside_square变量,然后我们将检查所生成的点是否位于圆内。 如果是,那么我们增加points_inside_circle变量:
plt.axes().set_aspect('equal')
plt.plot(1*np.cos(arc), 1*np.sin(arc))
for i in range(sample_size):
point = generate_points(square_size)
plt.plot(point[0], point[1], 'c.')
points_inside_square += 1
if is_in_circle(point, square_size):
points_inside_circle += 1
现在,我们使用compute_pi()函数计算π的值,该函数将打印出大约π的值:
print("Approximate value of pi is {}" .format(calculate_pi(points_inside_circle, points_inside_square)))
如果运行该程序,将得到如下所示的输出:
Approximate value of pi is 3.144
完整的程序如下所示:
import numpy as np
import math
import random
import matplotlib.pyplot as plt
%matplotlib inline
square_size = 1
points_inside_circle = 0
points_inside_square = 0
sample_size = 1000
arc = np.linspace(0, np.pi/2, 100)
def generate_points(size):
x = random.random()*size
y = random.random()*size
return (x, y)
def is_in_circle(point, size):
return math.sqrt(point[0]**2 + point[1]**2) <= size
def compute_pi(points_inside_circle, points_inside_square):
return 4 * (points_inside_circle / points_inside_square)
plt.axes().set_aspect('equal')
plt.plot(1*np.cos(arc), 1*np.sin(arc))
for i in range(sample_size):
point = generate_points(square_size)
plt.plot(point[0], point[1], 'c.')
points_inside_square += 1
if is_in_circle(point, square_size):
points_inside_circle += 1
print("Approximate value of pi is {}" .format(calculate_pi(points_inside_circle, points_inside_square)))
因此,蒙特卡洛方法通过使用随机采样来近似pi的值。 我们使用正方形内部生成的随机点(样本)估计pi的值。 采样量越大,我们的近似值越好。 现在,我们将看到如何在 RL 中使用蒙特卡洛方法。
蒙特卡洛预测
在 DP 中,我们通过使用值迭代和策略迭代来解决马尔可夫决策过程(MDP)。 这两种技术都需要转换和奖励概率才能找到最佳策略。 但是,当我们不知道转移和奖励概率时,如何解决 MDP? 在这种情况下,我们使用蒙特卡洛方法。 蒙特卡洛方法仅需要状态,动作和奖励的样本序列。 蒙特卡罗方法仅适用于剧集任务。 由于蒙特卡洛不需要任何模型,因此称为无模型学习算法。
蒙特卡洛方法的基本思想非常简单。 您还记得我们在上一章第 3 章,“马尔可夫决策过程和动态规划”中如何定义最佳值函数以及如何得出最佳策略吗?
值函数基本上是状态S与策略π的预期收益。 在这里,我们使用均值回报代替预期回报。
因此,在蒙特卡洛预测中,我们通过取均值回报而不是期望回报来近似值函数。
使用蒙特卡洛预测,我们可以估计任何给定策略的值函数。 蒙特卡洛预测中涉及的步骤非常简单,如下所示:
- 首先,我们将随机值初始化为我们的值函数
- 然后我们初始化一个称为
return的空列表来存储我们的回报 - 然后针对剧集中的每个状态,我们计算收益
- 接下来,我们将回报附加到回报清单中
- 最后,我们将收益平均值作为我们的值函数
以下流程图使其更简单:

蒙特卡洛预测算法有两种类型:
- 首次访问蒙特卡洛
- 每次访问蒙特卡洛
首次访问蒙特卡洛
如我们所见,在蒙特卡洛方法中,我们通过取平均收益来近似值函数。 但是在首次访问 MC 方法中,我们仅在剧集中首次访问状态时才对返回值进行平均。 例如,假设一个智能体正在玩蛇和梯子游戏,那么如果该智能体被蛇咬伤,它很有可能会返回到该状态。 当智能体重新访问状态时,我们不考虑平均回报。 我们仅在智能体首次访问该状态时才考虑平均回报。
每次访问蒙特卡洛
在蒙特卡洛的每次访问中,我们平均将剧集中每次访问状态的收益均值化。 考虑相同的蛇和梯子游戏示例:如果智能体在蛇咬之后返回到相同的状态,尽管智能体正在重新访问状态,但我们可以将其视为平均收益。 在这种情况下,我们平均每次智能体访问该状态时的回报。
让我们使用蒙特卡洛玩二十一点
现在,让我们通过二十一点游戏更好地了解蒙特卡洛。 二十一点,也称为 21,是在赌场玩的一种流行的纸牌游戏。 游戏的目标是使您的所有牌的总和接近 21 并且不超过 21。牌 J,K 和 Q 的值为 10。王牌的值为 1 或 11;王牌的值为 1 或 11。 这取决于玩家的选择。 其余卡(1 至 10)的值与它们显示的数字相同。
游戏规则非常简单:
-
可以与一个或多个玩家和一个发牌人一起玩游戏。
-
每个玩家仅与庄家竞争,而不与其他玩家竞争。
-
最初,给玩家一张两张牌。 这两个卡都面朝上,即对其他人可见。
-
庄家也得到了两张牌。 一张卡面朝上,另一张面朝下。 也就是说,发牌人只显示他的一张牌。
-
如果在收到两张牌后,一张牌的总和为 21(例如,一位牌手已收到
10 + 11 = 21的杰克和王牌),则称其为自然或黑杰克,玩家获胜。 -
如果发牌人在收到两张卡后立即的总卡数也为 21,则称为两可(Draw),因为它们两张都有 21 张。
-
在每个回合中,玩家决定是否需要另一张纸牌来总计接近 21 张纸牌。
-
如果玩家需要纸牌,则称其为拿牌(Hit)。
-
如果玩家不需要纸牌,则称为停牌(Stand)。
-
如果玩家的纸牌总数超过 21,则称为胀死(Bust); 那么发牌者将赢得比赛。
让我们通过玩来更好地了解二十一点。 我让你成为玩家,我是智能体:

在上图中,我们有一个参与者和一个庄家。 他们两个都有两张卡。 玩家的两张牌都朝上(可见),而发牌者的一张牌朝上(可见),另一张牌朝下(不可见)。 在第一轮中,您得到了两张卡,例如一个千斤顶和一个数字 7,即(10 + 7 = 17),而我作为发牌人只会向您显示一张数字 2。 面朝下。 现在,您必须决定要击中(需要另一张牌)还是站起来(不需要另一张牌)。 如果您选择击中并接收数字 3,您将获得10 + 7 + 3 = 20(接近 21),您将获胜:

但是,如果您收到一张卡,说出数字 7,则10 + 7 + 7 = 24,超过了 21。然后被称为破产,您输了游戏。 如果您决定站立使用初始卡,则只有10 + 7 = 17。然后我们将检查智能体的卡总和。 如果它大于 17 且不超过 21,则智能体赢,否则您赢:

这里的奖励是:
- 如果玩家赢得比赛,则为 +1
- 如果玩家输了则为 -1
- 如果游戏是平局,则为 0
可能的操作是:
- 拿牌:如果玩家需要纸牌
- 停牌:如果玩家不需要纸牌
玩家必须决定一张王牌的值。 如果玩家的纸牌总数为 10,并且在击中后获得一张王牌,则可以将其视为 11,而10 + 11 = 21。但是,如果玩家的纸牌总数为 15,并且在击中后,则获得一张王牌。 ,如果他将其视为 11 且15 + 11 = 26,则表示破产。 如果玩家拥有一张王牌,我们可以将其称为可用王牌; 玩家可以将其视为 11,而不会破产。 如果玩家通过将王牌视为 11 来破产,则称为不可用王牌。
现在,我们将看到如何使用首次访问的蒙特卡洛算法来实现二十一点。
首先,我们将导入必要的库:
import gym
from matplotlib import pyplot
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from collections import defaultdict
from functools import partial
%matplotlib inline
plt.style.use('ggplot')
现在,我们将使用 OpenAI 的 Gym 创建二十一点环境:
env = gym.make('Blackjack-v0')
然后我们定义策略函数,该函数采用当前状态并检查分数是否大于或等于2o; 如果是,则返回0,否则返回1。 也就是说,如果得分大于或等于20,我们将保持(0)或达到(1):
def sample_policy(observation):
score, dealer_score, usable_ace = observation
return 0 if score >= 20 else 1
现在,我们将了解如何生成剧集。 剧集是游戏的一个回合。 我们将逐步看到它,然后看完整函数。
我们将状态,动作和奖励定义为列表,并使用env.reset初始化环境并存储观察变量:
states, actions, rewards = [], [], []
observation = env.reset()
然后,执行以下操作,直到到达最终状态,即直到剧集结束为止:
- 将观察值追加到状态列表:
states.append(observation)
- 现在,我们使用
sample_policy函数创建一个动作,并将这些动作附加到action列表中:
action = sample_policy(observation)
actions.append(action)
- 然后,对于环境中的每个步骤,我们都存储
state,reward和done(指定是否达到最终状态),并将奖励添加到reward列表中:
observation, reward, done, info = env.step(action)
rewards.append(reward)
- 如果我们到达最终状态,那么我们将中断:
if done:
break
- 完整的
generate_episode函数如下:
def generate_episode(policy, env):
states, actions, rewards = [], [], []
observation = env.reset()
while True:
states.append(observation)
action = policy(observation)
actions.append(action)
observation, reward, done, info = env.step(action)
rewards.append(reward)
if done:
break
return states, actions, rewards
这就是我们生成剧集的方式。 我们如何玩游戏? 为此,我们需要知道每个状态的值。 现在,我们将看到如何使用首次访问蒙特卡洛方法获取每个状态的值。
首先,我们将空值表初始化为用于存储每个状态的值的字典:
value_table = defaultdict(float)
然后,对于一定数量的剧集,我们执行以下操作:
- 首先,我们生成剧集并存储状态和奖励; 我们将回报初始化为
0,这是奖励的总和:
states, _, rewards = generate_episode(policy, env)
returns = 0
- 然后,对于每个步骤,我们将奖励存储到变量
R中,并声明为S,然后将收益计算为奖励总和:
for t in range(len(states) - 1, -1, -1):
R = rewards[t]
S = states[t]
returns += R
- 现在,我们进行首次访问蒙特卡洛; 我们会在访问时间内检查是否正在访问该剧集。 如果是的话,我们只取收益的平均值并将状态值指定为收益的平均值:
if S not in states[:t]:
N[S] += 1
value_table[S] += (returns - V[S]) / N[S]
- 查看完整函数来更好地理解:
def first_visit_mc_prediction(policy, env, n_episodes):
value_table = defaultdict(float)
N = defaultdict(int)
for _ in range(n_episodes):
states, _, rewards = generate_episode(policy, env)
returns = 0
for t in range(len(states) - 1, -1, -1):
R = rewards[t]
S = states[t]
returns += R
if S not in states[:t]:
N[S] += 1
value_table[S] += (returns - V[S]) / N[S]
return value_table
- 我们可以得到每个状态的值:
value = first_visit_mc_prediction(sample_policy, env, n_episodes=500000)
- 让我们看看一些状态的值:
print(value)
defaultdict(float,
{(4, 1, False): -1.024292170184644,
(4, 2, False): -1.8670191351012455,
(4, 3, False): 2.211363314854649,
(4, 4, False): 16.903201033000823,
(4, 5, False): -5.786238030898542,
(4, 6, False): -16.218211752577602,
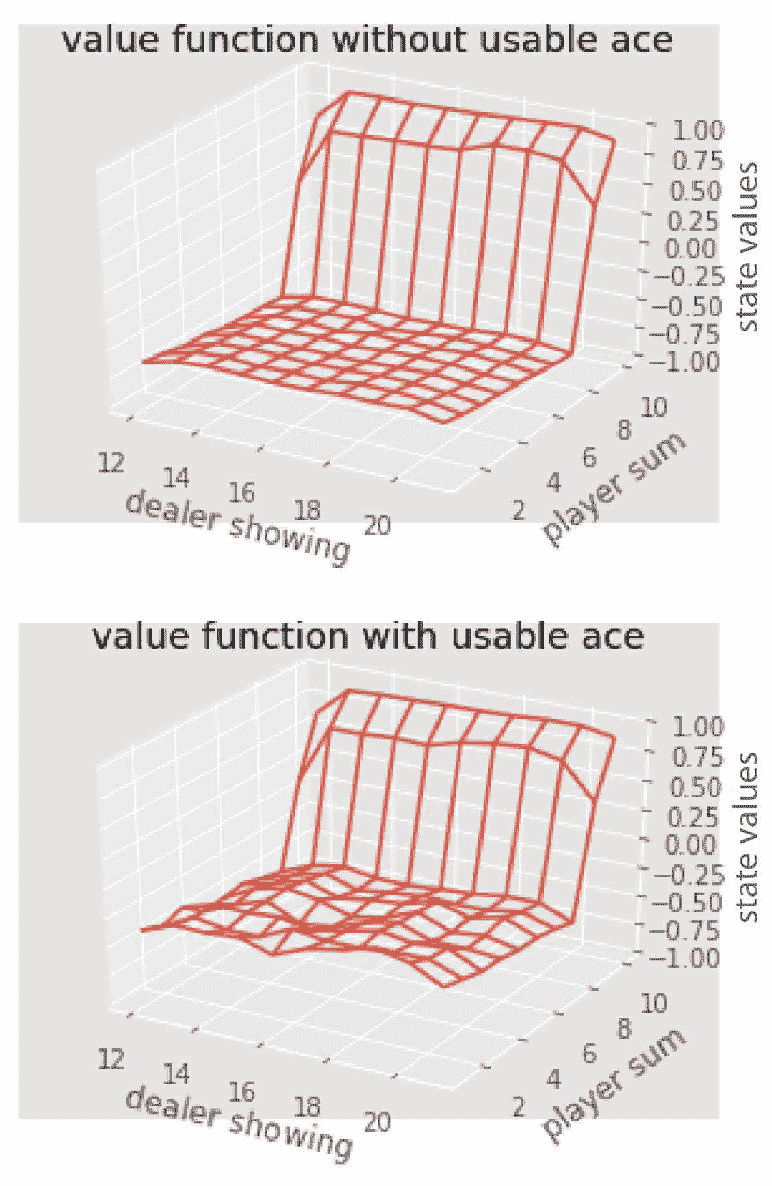
我们还可以绘制状态值以查看其收敛方式,如下所示:
完整的代码如下:
import numpy
import gym
from matplotlib import pyplot
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from collections import defaultdict
from functools import partial
%matplotlib inline
plt.style.use('ggplot')
## Blackjack Environment
env = gym.make('Blackjack-v0')
env.action_space, env.observation_space
def sample_policy(observation):
score, dealer_score, usable_ace = observation
return 0 if score >= 20 else 1
def generate_episode(policy, env):
states, actions, rewards = [], [], []
observation = env.reset()
while True:
states.append(observation)
action = sample_policy(observation)
actions.append(action)
observation, reward, done, info = env.step(action)
rewards.append(reward)
if done:
break
return states, actions, rewards
def first_visit_mc_prediction(policy, env, n_episodes):
value_table = defaultdict(float)
N = defaultdict(int)
for _ in range(n_episodes):
states, _, rewards = generate_episode(policy, env)
returns = 0
for t in range(len(states) - 1, -1, -1):
R = rewards[t]
S = states[t]
returns += R
if S not in states[:t]:
N[S] += 1
value_table[S] += (returns - value_table[S]) / N[S]
return value_table
def plot_blackjack(V, ax1, ax2):
player_sum = numpy.arange(12, 21 + 1)
dealer_show = numpy.arange(1, 10 + 1)
usable_ace = numpy.array([False, True])
state_values = numpy.zeros((len(player_sum),
len(dealer_show),
len(usable_ace)))
for i, player in enumerate(player_sum):
for j, dealer in enumerate(dealer_show):
for k, ace in enumerate(usable_ace):
state_values[i, j, k] = V[player, dealer, ace]
X, Y = numpy.meshgrid(player_sum, dealer_show)
ax1.plot_wireframe(X, Y, state_values[:, :, 0])
ax2.plot_wireframe(X, Y, state_values[:, :, 1])
for ax in ax1, ax2:
ax.set_zlim(-1, 1)
ax.set_ylabel('player sum')
ax.set_xlabel('dealer showing')
ax.set_zlabel('state-value')
fig, axes = pyplot.subplots(nrows=2, figsize=(5, 8), subplot_kw={'projection': '3d'})
axes[0].set_title('value function without usable ace')
axes[1].set_title('value function with usable ace')
plot_blackjack(value, axes[0], axes[1])
蒙特卡洛控制
在蒙特卡洛预测中,我们已经看到了如何估计值函数。 在蒙特卡洛控制中,我们将看到如何优化值函数,即如何使值函数比估计值更准确。 在控制方法中,我们遵循一种称为通用策略迭代的新型迭代,其中策略评估和策略改进彼此交互。 它基本上是在策略评估和改进之间循环的,也就是说,相对于值函数而言,策略总是会得到改进,而根据策略,值函数总是会得到改善。 它继续这样做。 当没有变化时,可以说策略和值函数已经达到收敛,即发现了最优值函数和最优策略:

现在,我们将看到如下不同的蒙特卡洛控制算法。
蒙特卡洛探索
与 DP 方法不同,这里我们不估计状态值。 相反,我们专注于动作值。 当我们知道环境模型时,仅状态值就足够了。 由于我们不了解模型动态,因此这不是单独确定状态值的好方法。
估计动作值比估计状态值更直观,因为状态值根据我们选择的策略而变化。 例如,在二十一点游戏中,假设我们处于某些纸牌为 20 的状态。该状态的值是什么? 这完全取决于策略。 如果我们选择策略作为命中目标,那将不是一个好的状态,而且此状态的值非常低。 但是,如果我们选择我们的策略作为立场,那肯定是一个好的国家。因此,状态的值取决于我们选择的策略。 因此,估计操作的值而不是状态的值更为重要。
我们如何估计作用值? 还记得我们在第 3 章,“马尔可夫决策过程和动态规划”中学习的Q函数吗? 表示为Q(s, a)的Q函数用于确定特定状态下的动作有多好。 它基本上指定了状态-动作对。
但是,这里出现了探索的问题。如果我们还没有处于状态状态值,我们如何知道状态状态值? 如果我们不采取所有可能的措施探索所有状态,我们可能会错过丰厚的回报。
假设在二十一点游戏中,我们处于纸牌总数为 20 的状态。如果我们仅尝试拿牌动作,我们将获得负数奖励,我们将得到负的奖励。但是,如果我们尝试停牌动作,我们将获得积极的回报,这实际上是最好的状态。因此,每次进入此特定状态 ,我们站立而不是受到打击。 为了让我们知道哪个是最佳操作,我们必须探索每种状态下的所有可能操作以找到最佳值。 我们应该怎么做?
让我介绍一个名为探索起始的蒙特卡洛,这意味着对于每个剧集,我们都将随机状态作为初始状态开始并执行操作。 因此,如果我们有大量的剧集,我们可能会以所有可能的动作覆盖所有状态。 它也称为 MC-ES 算法。
MC-ES 算法非常简单,如下所示:
-
我们首先使用一些随机值初始化
Q函数和策略,然后我们初始化返回到空列表的过程 -
然后,我们以随机初始化的策略开始
-
然后,我们计算该剧集中发生的所有唯一状态操作对的收益,并将收益附加到我们的收益清单中
-
我们只为唯一的状态-动作对计算返回值,因为同一状态-动作对多次出现在剧集中,并且没有多余的信息点
-
然后,我们对返回列表中的返回值取平均值,然后将该值分配给我们的
Q函数 -
最后,我们将为一个状态选择一个最佳策略,为该状态选择具有最大
Q(s, a)的操作 -
我们将永久重复整个过程,或者重复进行多次,以便涵盖所有不同的状态和动作对
这是一个流程图:

策略性蒙特卡洛控制
在开始进行蒙特卡洛探索时,我们将探索所有状态-动作对,并选择能给我们带来最大值的对。 但是考虑一下我们拥有大量状态和行动的情况。 在这种情况下,如果我们使用 MC-ES 算法,则将花费大量时间来探索状态和动作的所有组合并选择最佳状态和动作。 我们如何克服这个问题? 有两种不同的控制算法。 上策略和下策略。 在基于策略的蒙特卡洛控制中,我们使用ε贪婪策略。 让我们了解什么是贪婪算法。
贪婪的算法会选择当时可用的最佳选择,尽管当您考虑整个问题时,该选择可能不是最佳选择。 考虑您要从数字列表中找到最小的数字。 您可以将列表分为三个子列表,而不是直接从列表中找到最小的数字。 然后,您将在每个子列表中找到最小的数字(局部最优值)。 考虑整个列表时,在一个子列表中找到的最小数目可能不是最小数目(全局最优)。 但是,如果您表现得很贪婪,那么您将仅在当前子列表中看到最小的数字(此刻),然后将其视为最小的数字。
贪婪策略表示在所探索的行动中的最佳行动。 最佳动作是具有最高值的动作。
假设我们已经探索了状态 1 中的一些动作,如 Q 表所示:
| 状态 | 动作 | 值 |
|---|---|---|
| 状态 1 | 动作 0 | 0.5 |
| 状态 1 | 动作 1 | 0.1 |
| 状态 1 | 动作 2 | 0.8 |
如果我们表现出贪婪的态度,那么我们将从所有探索的动作中挑选出具有最大值的动作。 在前面的情况中,我们具有较高值的动作 2,因此我们选择该动作。 但是状态 1 中可能还有其他我们尚未探讨的动作,可能值最高。 因此,我们必须在所有探索的动作中寻找最佳动作或利用最佳动作。 这就是所谓的探索利用困境。 假设您听过爱德·希兰(Ed Sheeran),并且非常喜欢他,所以您因为喜欢音乐而一直只听(探索)爱德·希兰(Ed Sheeran)。 但是,如果您尝试听其他艺术家的音乐,您可能会喜欢比 Ed Sheeran(探索)更好的人。 关于您是否只需要听 Ed Sheeran(利用)还是尝试听不同的艺术家以查看您是否喜欢他们(利用)的这种困惑称为探索利用难题。
因此,为了避免这种困境,我们引入了一种称为ε贪婪策略的新策略。 在这里,所有动作均以非零概率(ε)进行尝试。 对于概率ε,我们随机地探索不同的动作,而对于概率 1,我们选择具有最大值的动作,即,我们不进行任何探索。 因此,我们不仅会以概率ε始终利用最佳行动,而且还会随机探索不同的行动。 如果epsilon的值设置为零,那么我们将不做任何探索。 这只是贪婪的策略,如果将epsilon的值设置为 1,则它将始终仅进行探索。epsilon的值会随着时间的流逝而衰减,因为我们不想永远探索。 因此,随着时间的流逝,我们的策略会采取良好的行动:

假设我们将epsilon的值设置为0.3。 在下面的代码中,我们从均匀分布中生成一个随机值,如果该值小于epsilon值,即 0.3,则选择一个随机动作(以这种方式,我们搜索一个不同的动作)。 如果来自均匀分布的随机值大于 0.3,则我们选择具有最佳值的操作。 因此,通过这种方式,我们以概率epsilon探索了以前从未见过的动作,并从概率为 1 epsilon的探索动作中选择了最佳动作:
def epsilon_greedy_policy(state, epsilon):
if random.uniform(0,1) < epsilon:
return env.action_space.sample()
else:
return max(list(range(env.action_space.n)), key = lambda x: q[(state,x)])
让我们想象一下,我们已经使用ε贪婪策略探索了状态 1 中的其他动作(尽管不是所有动作对),并且我们的 Q 表如下所示:
| 状态 | 动作 | 值 |
|---|---|---|
| 状态 1 | 动作 0 | 0.5 |
| 状态 1 | 动作 1 | 0.1 |
| 状态 1 | 动作 2 | 0.8 |
| 状态 1 | 动作 4 | 0.93 |
在状态 1 中,动作 4 具有比我们之前发现的动作 2 高的值。 因此,在ε贪婪策略下,我们以概率epsilon寻找不同的动作,并以概率为 1 epsilon寻找最佳动作。
策略性蒙特卡洛方法涉及的步骤非常简单:
-
首先,我们初始化随机策略和随机 Q 函数。
-
然后,我们初始化一个称为
return的列表,用于存储回报。 -
我们使用随机策略
π生成剧集。 -
我们将剧集中发生的每个状态操作对的返回存储到返回列表中。
-
然后,我们对返回列表中的返回值取平均值,然后将该值分配给
Q函数。 -
现在,由
ε决定由状态s选择动作a的可能性。 -
如果概率为
1-ε,我们将选择最大Q值的动作。 -
如果概率为
ε,我们将探索不同的动作。
脱离策略的蒙特卡洛控制
非策略性蒙特卡洛是另一种有趣的蒙特卡洛控制方法。 在这种方法中,我们有两种策略:一种是行为策略,另一种是目标策略。 在非策略方法中,智能体遵循一项策略,但与此同时,它会尝试学习和改进另一种策略。 智能体遵循的策略称为行为策略,智能体尝试评估和改进的策略称为目标策略。 行为与目标策略完全无关。 行为策略探索所有可能的状态和动作,这就是为什么将行为策略称为软策略,而将目标策略称为贪心策略(它选择具有最大值的策略)的原因。
我们的目标是为目标策略π估计Q函数,但我们的智能体使用完全不同的策略(称为行为策略μ)进行操作。 我们现在能做什么? 我们可以通过使用μ中发生的常见事件来估计π的值。 我们如何估计这两个策略之间的共同点? 我们使用一种称为重要性抽样的新技术。 这是一种在给定来自另一个分布的样本的情况下从一个分布估计值的技术。
重要抽样有两种类型:
- 普通重要性抽样
- 加权重要性抽样
在普通重要性抽样中,我们基本上采用行为策略和目标策略获得的收益之比,而在加权重要性抽样中,我们采用加权平均值,而C是权重的累加和。
让我们一步一步看一下:
-
首先,我们将
Q(s, a)初始化为随机值,并将C(s, a)初始化为0,权重w为1。 -
然后我们选择目标策略,这是一个贪婪策略。 这意味着它将从
Q表中选取具有最大值的策略。 -
我们选择行为策略。 行为策略不是贪婪的,它可以选择任何状态-行为对。
-
然后,我们开始我们的剧集,并根据我们的行为策略在
s状态下执行动作a,并存储奖励。 我们重复此操作直到剧集结束。 -
现在,对于剧集中的每个状态,我们执行以下操作:
-
我们将计算回报
G。 我们知道回报是折扣奖励的总和:G = 折扣因子 * G + 奖励。 -
然后我们将
C(s, a)更新为C(s, a) + C(s, a) + w。 -
我们更新
Q(s, a):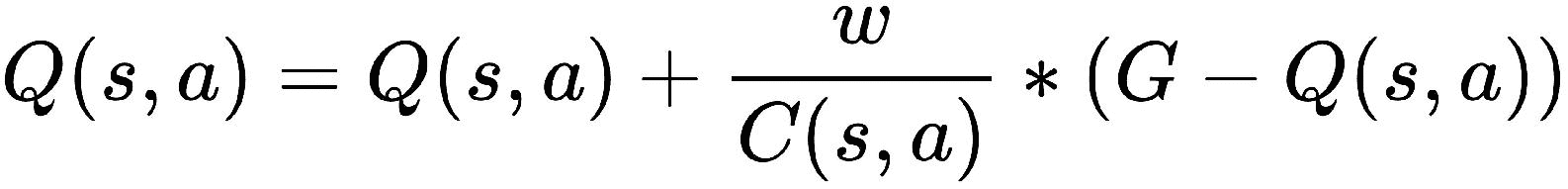
-
我们更新
w的值:
-
总结
在本章中,我们了解了蒙特卡洛方法的工作原理,以及当我们不了解环境模型时如何使用它来解决 MDP。 我们研究了两种不同的方法:一种是用于估计值函数的蒙特卡洛预测,另一种是用于优化值函数的蒙特卡洛控制。
我们在蒙特卡洛预测中研究了两种不同的方法:首次访问蒙特卡洛预测,其中只有在剧集中首次访问该状态时,我们才对收益进行平均;以及每次访问蒙特卡洛方法,其中每次在剧集中访问状态时,我们都将收益平均。
在蒙特卡洛控制方面,我们研究了不同的算法。 我们首先遇到了 MC-ES 控件,该控件用于覆盖所有状态-动作对。 我们研究了策略上的 MC 控制(它使用ε贪婪策略)和策略外的 MC 控制(一次使用两个策略)。
在下一章第 5 章,“时间差异学习”中,我们将介绍一种不同的无模型学习算法。
问题
问题列表如下:
- 什么是蒙特卡洛方法?
- 使用蒙特卡洛方法估计黄金分割率的值。
- 蒙特卡洛预测的用途是什么?
- 首次访问 MC 和每次访问 MC 有什么区别?
- 为什么我们要估计状态作用值?
- 策略上的 MC 控制和策略外的 MC 控制有什么区别?
- 编写一些 Python 代码,以使用策略性 MC 控件玩二十一点游戏。
进一步阅读
请参考以下链接:
五、时间差异学习
在上一章第四章,“使用蒙特卡洛方法的游戏”中,我们了解了有趣的蒙特卡洛方法,该方法用于解决马尔可夫决策过程(MDP),而不像动态规划那样预先未知环境的模型动态。 我们研究了蒙特卡洛预测方法,该方法用于预测值函数,而控制方法用于进一步优化值函数。 但是蒙特卡洛方法存在一些陷阱。 它仅适用于情景任务。 如果剧集很长,那么我们必须等待很长时间才能计算值函数。 因此,我们将使用另一种有趣的算法,称为时差(TD)学习,这是一种无模型的学习算法:不需要事先知道模型动态,它也可以用于非临时性任务。
在本章中,您将学习:
- TD 学习
- Q 学习
- SARSA
- 使用 Q 学习和 SARSA 调度出租车
- Q 学习和 SARSA 之间的区别
TD 学习
TD 学习算法由 Sutton 于 1988 年提出。该算法兼顾了蒙特卡洛方法和动态规划(DP)的优点。 像蒙特卡洛方法一样,它不需要模型动态,而像 DP 一样,它不需要等到剧集结束就可以估计值函数。 取而代之的是,它基于先前学习的估计值来估计当前估计值,这也称为自举。 如果您在蒙特卡洛方法中看到没有引导程序,那么我们仅在剧集结束时进行估计,但在 TD 方法中我们可以进行引导。
TD 预测
就像我们在蒙特卡洛预测中所做的一样,在 TD 预测中,我们尝试预测状态值。 在蒙特卡洛预测中,我们仅通过取均值收益来估计值函数。 但是在 TD 学习中,我们通过当前状态更新先前状态的值。 我们应该怎么做? TD 学习使用一种称为 TD 更新规则的东西来更新状态值,如下所示:

先前状态的值 = 先前状态的值 + 学习率(奖励 + 折扣因子(当前状态的值)- 先前状态的值)
这个方程实际上是什么意思?
如果您直观地想到此方程,则实际上是实际奖励(r + γV(s'))和预期奖励(V(s))之间的差乘以学习率α。 学习率代表什么? 学习率(也称为步长)对于收敛很有用。
你注意到了吗? 由于我们将实际值和预测值之差作为r + γV(s') - V(s),因此实际上是一个误差。 我们可以称其为 TD 误差。 在多次迭代中,我们将尝试最小化此误差。
让我们通过前面几章中的冰湖示例来了解 TD 预测。 接下来显示的是冰冻的湖泊环境。 首先,对于所有状态,我们将值函数初始化为0,就像在V(S)中将其初始化为0一样,如以下状态值图所示 :
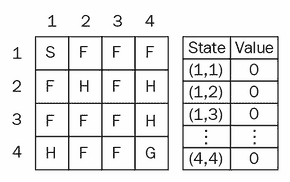
假设我们处于s = (1, 1)的初始状态,我们将采取正确的操作并移至下一个状态s' = (1, 2),并获得 -0.3 的奖励(r)。 我们如何使用此信息来更新状态的值?
回忆一下 TD 更新公式:

让我们将学习率(α)视为0.1,将折扣率(γ)视为 0.5; 我们知道状态(1, 1)的值(如V(S)中的值)为 0,而下一个状态(1, 2)的值与V(S)一样,也是0。 我们获得的奖励(r)为 -0.3。 我们将其替换为 TD 规则,如下所示:
V(s) = 0 + 0.1 * (-0.3 + 0.5 (0) - 0)
V(s) = -0.03
因此,我们在值表中将状态(1, 1)的值更新为-0.03,如下图所示:

现在我们以(1, 2)的状态处于s的状态,我们将采取正确的操作并移至下一个状态s' = (1, 3)并获得奖励r = -0.3。 我们现在如何更新状态(1, 2)的值?
像我们之前所做的那样,我们将 TD 更新方程中的值替换为:
V(s) = 0 + 0.1 * (-0.3 + 0.5(0) - 0)
V(s) = -0.03
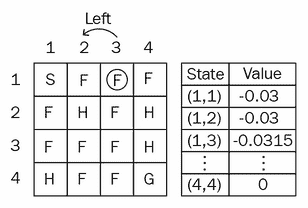
因此,我们将状态(1, 2)的值设置为-0.03,并在值表中对其进行更新,如下所示:

现在我们处于s = (1, 3)状态; 假设我们要采取行动了。 我们再次回到该状态s' = (1, 2),我们将获得奖励r = -0.3。 此处,状态(1, 3)的值为0,下一个状态(1, 2)的值为值表中的-0.03。
现在我们可以更新状态(1, 3)的值,如下所示:
V(s) = 0 + 0.1 * (-0.3 + 0.5 * (-0.03) - 0))
V(s) = 0.1 * -0.315
V(s) = -0.0315
因此,我们在值表中将状态(1, 3)的值更新为-0.0315,如下所示:
以类似的方式,我们使用 TD 更新规则更新所有状态的值。 TD 预测算法涉及的步骤如下:
- 首先,我们将
V(S)初始化为0或一些任意值 - 然后我们开始该剧集,并在剧集中的每个步骤中,在状态
S中执行动作A,并获得奖励R,然后移至下一个状态s' - 现在,我们使用 TD 更新规则更新先前状态的值
- 重复步骤
3和4,直到达到最终状态
TD 控制
在 TD 预测中,我们估计了值函数。 在 TD 控制中,我们优化了值函数。 对于 TD 控制,我们使用两种控制算法:
- 无策略学习算法:Q 学习
- 策略学习算法:SARSA
Q 学习
现在,我们将研究称为 Q 学习的非常流行的非策略性 TD 控制算法。 Q 学习是一种非常简单且广泛使用的 TD 算法。 在控制算法中,我们不在乎状态值。 在这里,在 Q 学习中,我们关心的是状态-动作值对-在状态S下执行动作A的效果。
我们将根据以下公式更新Q值:

前面的公式与 TD 预测更新规则相似,只是有一点点差异。 我们将逐步详细介绍这一点。 Q 学习涉及的步骤如下:
- 首先,我们将
Q函数初始化为一些任意值 - 我们使用
ε贪婪策略(ε > 0)从某个状态采取了一项行动,并将其移至新的状态 - 我们通过遵循更新规则来更新先前状态的
Q值:
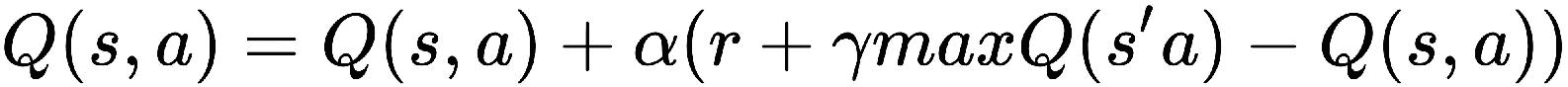
- 重复步骤
2和3,直到达到最终状态
现在,我们将使用不同的步骤来理解算法。
考虑相同的冻湖示例。 假设我们处于状态(3, 2),并且有两个动作(左和右)。 现在让我们参考该图,并将其与ε贪婪策略进行比较:

在“Q 学习”中,我们使用ε贪婪策略选择一个动作。 我们要么探索概率为ε的新动作,要么选择概率为1ε的最佳动作。 假设我们选择一个概率ε,并探索一个新的动作向下,然后选择该动作:

现在,我们已经对状态(3, 2)执行了向下操作,并使用ε贪婪策略达到了新状态(4, 2),我们如何使用我们的更新规则来更新先前状态(3, 2)的值? 这很简单。 查看Q表,如下所示:

让我们将alpha视为0.1,并将折扣因子视为1:
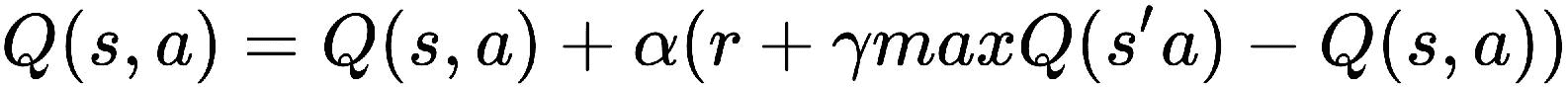
Q( (3,2) down) = Q( (3,2), down ) + 0.1 ( 0.3 + 1 max [Q( (4,2) action) ]- Q( (3,2), down)
我们可以说具有向下作用的状态(3, 2)的值,例如Q((3, 2), down)的值为Q表中的0.8。
状态(4, 2)的最大值Q((4, 2), op)是什么? 我们仅研究了三个动作(向上,向下和向右),因此我们将仅基于这些动作来获取最大值。 (此处,我们将不执行epsilon贪婪策略;我们仅选择具有最大值的操作。)
因此,基于先前的Q表,我们可以将值替换为:
Q( (3,2), down) = 0.8 + 0.1 ( 0.3 + 1 max [0.3, 0.5, 0.8] - 0.8 )
= 0.8 + 0.1 ( 0.3 + 1 (0.8) - 0.8)
= 0.83
因此,我们将Q((3, 2), down)的值更新为0.83。
请记住,在选择要采取的操作时,我们将执行ε贪婪策略:我们要么探索具有概率epsilon的新操作,要么采取具有最大值的概率 1 epsilon。 在更新 Q 值时,我们不执行ε贪婪策略,我们仅选择具有最大值的操作。
现在我们处于状态(4, 2),我们必须执行一个动作。 我们应该执行什么动作? 我们决定基于ε贪婪策略,要么探索具有概率epsilon的新操作,要么选择具有概率 1-epsilon 的最佳操作。 假设我们选择概率1-ε,然后选择最佳操作。 因此,在(4, 2)中,向右的操作具有最大值。 因此,我们将选择向右操作:
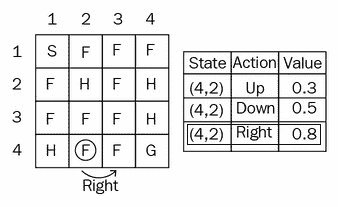
现在我们处于状态(4, 3),因为我们对状态(4, 2)采取了向右动作。 我们如何更新先前状态的值? 像这样:
Q( (4,2), right) = Q( (4,2), right ) + 0.1 ( 0.3 + 1 max [Q( (4,3) action) ]- Q( (4,2), right)
如果您查看下面的Q表,对于状态(4, 3),我们仅探讨了两个操作(向上和向下),因此我们仅根据这些操作得出最大值。 (这里,我们将不执行ε贪婪策略;我们只选择具有最大值的操作):
Q ( (4,2), right) = Q((4,2),right) + 0.1 (0.3 + 1 max [ (Q (4,3), up) , ( Q(4,3),down) ] - Q ((4,2), right )
Q ( (4,2), right) = 0.8 + 0.1 (0.3 + 1 max [ 0.1,0.3] - 0.8)
= 0.8 + 0.1 (0.3 + 1(0.3) - 0.8)
= 0.78
查看下面的Q表:
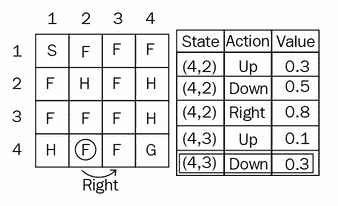
现在我们将状态Q((4,2), right)的值更新为0.78。
因此,这就是我们在 Q 学习中获得状态作用值的方式。 为了决定采取什么行动,我们使用ε贪婪策略,并在更新Q值时,我们只选择最大的行动; 这是流程图:

使用 Q 学习解决出租车问题
为了演示该问题,我们假设智能体是驱动程序。 有四个地点,智能体必须在一个地点接客并在另一地点下车。 智能体将获得 +20 积分作为成功下车的奖励,而每走一步便获得 -1 积分。 该智能体还将因非法取送丢掉 -10 分。 因此,我们智能体的目标是学会在短时间内在正确的位置上落客而不增加非法乘客。
这里显示的环境中,字母(R,G,Y,B)代表不同的位置,并且一个小矩形是驾驶出租车的智能体:

让我们看一下编码部分:
import gym
import random
现在,我们使用gym创建环境:
env = gym.make("Taxi-v1")
这种出租车的环境如何? 像这样:
env.render()
好的,首先让我们初始化学习率alpha,epsilon值和gamma:
alpha = 0.4
gamma = 0.999
epsilon = 0.017
然后我们初始化一个 Q 表; 它有一个字典,将状态-操作值对存储为(状态,操作):
q = {}
for s in range(env.observation_space.n):
for a in range(env.action_space.n):
q[(s,a)] = 0.0
我们将通过 Q 学习更新规则定义用于更新 Q 表的函数; 如果您看下面的函数,您将看到我们采取的状态/动作对具有最大值的动作并将其存储在qa变量中。 然后,我们通过更新规则更新先前状态的Q值,如下所示:

def update_q_table(prev_state, action, reward, nextstate, alpha, gamma):
qa = max([q[(nextstate, a)] for a in range(env.action_space.n)])
q[(prev_state,action)] += alpha * (reward + gamma * qa -q[(prev_state,action)])
然后,我们定义一个函数以执行ε贪婪策略,并在其中传递状态和epsilon值。 我们生成一些均匀分布的随机数,如果该数小于epsilon,则在状态中探索不同的动作,否则我们将利用具有最大 q 值的动作:
def epsilon_greedy_policy(state, epsilon):
if random.uniform(0,1) < epsilon:
return env.action_space.sample()
else:
return max(list(range(env.action_space.n)), key = lambda x: q[(state,x)])
我们将结合所有这些函数,了解如何进行 Q 学习:
# For each episode
for i in range(8000):
r = 0
#first we initialize the environment
prev_state = env.reset()
while True:
#In each state we select action by epsilon greedy policy
action = epsilon_greedy_policy(prev_state, epsilon)
#then we take the selected action and move to the next state
nextstate, reward, done, _ = env.step(action)
#and we update the q value using the update_q_table() function
#which updates q table according to our update rule.
update_q_table(prev_state, action, reward, nextstate, alpha, gamma)
#then we update the previous state as next stat
prev_state = nextstate
#and store the rewards in r
r += reward
#If done i.e if we reached the terminal state of the episode
#if break the loop and start the next episode
if done:
break
print("total reward: ", r)
env.close()
完整的代码在这里给出:
import random
import gym
env = gym.make('Taxi-v1')
alpha = 0.4
gamma = 0.999
epsilon = 0.017
q = {}
for s in range(env.observation_space.n):
for a in range(env.action_space.n):
q[(s,a)] = 0
def update_q_table(prev_state, action, reward, nextstate, alpha, gamma):
qa = max([q[(nextstate, a)] for a in range(env.action_space.n)])
q[(prev_state,action)] += alpha * (reward + gamma * qa - q[(prev_state,action)])
def epsilon_greedy_policy(state, epsilon):
if random.uniform(0,1) < epsilon:
return env.action_space.sample()
else:
return max(list(range(env.action_space.n)), key = lambda x: q[(state,x)])
for i in range(8000):
r = 0
prev_state = env.reset()
while True:
env.render()
# In each state, we select the action by ε-greedy policy
action = epsilon_greedy_policy(prev_state, epsilon)
# then we perform the action and move to the next state, and
# receive the reward
nextstate, reward, done, _ = env.step(action)
# Next we update the Q value using our update_q_table function
# which updates the Q value by Q learning update rule
update_q_table(prev_state, action, reward, nextstate, alpha, gamma)
# Finally we update the previous state as next state
prev_state = nextstate
# Store all the rewards obtained
r += reward
#we will break the loop, if we are at the terminal
#state of the episode
if done:
break
print("total reward: ", r)
env.close()
SARSA
状态-动作-奖励-状态-动作(SARSA)是一种策略上的 TD 控制算法。 就像我们在 Q 学习中所做的一样,这里我们也关注状态-动作值,而不是状态-值对。 在 SARSA 中,我们根据以下更新规则更新 Q 值:

在前面的等式中,您可能会注意到,没有最大的Q(s', a'),就像在 Q 学习中一样。 这里只是Q(s', a')。 我们可以通过执行一些步骤来详细了解这一点。 SARSA 涉及的步骤如下:
- 首先,我们将
Q值初始化为一些任意值 - 我们通过
ε贪婪策略(ε > 0)选择一个动作,然后从一种状态转移到另一种状态 - 我们遵循更新规则
Q(s, a) = Q(s, a) + α(r + γQ(s', a') - Q(s, a))来更新Q值的先前状态,其中a'是由ε贪婪策略(ε > 0)选择的操作
现在,我们将逐步了解算法。 让我们考虑相同的冰冻湖的例子。 假设我们处于(4, 2)状态。 我们根据ε贪婪策略决定采取的措施。 假设我们使用概率为 1 epsilon并选择最佳操作,即向右:

现在,我们在状态(4, 2)下执行了向右动作之后,就处于(4, 3)状态。 我们如何更新先前状态(4, 2)的值? 让我们将alpha设为0.1,将奖励设为0.3和折扣系数1:
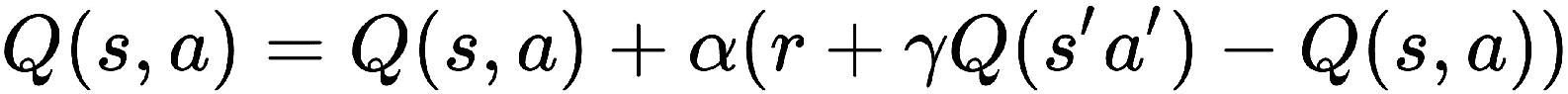
Q( (4,2), right) = Q( (4,2),right) + 0.1 ( 0.3 + 1 Q( (4,3), action)) - Q((4,2) , right)
我们如何选择Q((4, 3), action)的值? 在这里,与 Q 学习不同,我们不只是获取max Q((4, 3), action)。 在 SARSA 中,我们使用ε贪婪策略。
查看下面的 Q 表。 在状态(4, 3)中,我们探索了两个动作。 与 Q 学习不同,我们不会直接选择最大动作:

我们在这里也遵循ε贪婪策略。 我们要么以概率epsilon进行探索,要么以概率 1 epsilon进行利用。 假设我们选择概率ε并探索新的动作。 我们探索一个新动作向右,然后选择该动作:

Q ( (4,2), right) = Q((4,2),right) + 0.1 (0.3 + 1 (Q (4,3), right) - Q ((4,2), right )
Q ( (4,2), right) = 0.8 + 0.1 (0.3 + 1(0.9) - 0.8)
= 0.8 + 0.1 (0.3 + 1(0.9) - 0.8)
= 0.84
因此,这就是我们在 SARSA 中获取状态操作值的方式。 我们使用ε贪婪策略采取措施,并且在更新 Q 值的同时,我们使用ε贪婪策略采取措施。
下图说明了 SARSA 算法:

使用 SARSA 解决出租车问题
现在,我们将使用 SARSA 解决相同的出租车问题:
import gym
import random
env = gym.make('Taxi-v1')
另外,我们将初始化学习率gamma和epsilon。 Q 表有一个字典:
alpha = 0.85
gamma = 0.90
epsilon = 0.8
Q = {}
for s in range(env.observation_space.n):
for a in range(env.action_space.n):
Q[(s,a)] = 0.0
和往常一样,我们为探索定义了epsilon_greedy策略:
def epsilon_greedy(state, epsilon):
if random.uniform(0,1) < epsilon:
return env.action_space.sample()
else:
return max(list(range(env.action_space.n)), key = lambda x: Q[(state,x)])
现在,出现了实际的 SARSA 算法:
for i in range(4000):
#We store cumulative reward of each episodes in r
r = 0
#Then for every iterations, we initialize the state,
state = env.reset()
#then we pick up the action using epsilon greedy policy
action = epsilon_greedy(state,epsilon)
while True:
#Then we perform the action in the state and move the next state
nextstate, reward, done, _ = env.step(action)
#Then we pick up the next action using epsilon greedy policy
nextaction = epsilon_greedy(nextstate,epsilon)
#we calculate Q value of the previous state using our update rule
Q[(state,action)] += alpha * (reward + gamma * Q[(nextstate,nextaction)]-Q[(state,action)])
#finally we update our state and action with next action
# and next state
action = nextaction
state = nextstate
r += reward
#we will break the loop, if we are at the terminal
#state of the episode
if done:
break
env.close()
您可以运行该程序,然后查看 SARSA 如何找到最佳路径。
完整的程序在这里给出:
#Like we did in Q learning, we import necessary libraries and initialize environment
import gym
import random
env = gym.make('Taxi-v1')
alpha = 0.85
gamma = 0.90
epsilon = 0.8
#Then we initialize Q table as dictionary for storing the state-action values
Q = {}
for s in range(env.observation_space.n):
for a in range(env.action_space.n):
Q[(s,a)] = 0.0
#Now, we define a function called epsilon_greedy for performing action
#according epsilon greedy policy
def epsilon_greedy(state, epsilon):
if random.uniform(0,1) < epsilon:
return env.action_space.sample()
else:
return max(list(range(env.action_space.n)), key = lambda x: Q[(state,x)])
for i in range(4000):
#We store cumulative reward of each episodes in
r = 0
#Then for every iterations, we initialize the state,
state = env.reset()
#then we pick up the action using epsilon greedy policy
action = epsilon_greedy(state,epsilon)
while True:
#Then we perform the action in the state and move the next state
nextstate, reward, done, _ = env.step(action)
#Then we pick up the next action using epsilon greedy policy
nextaction = epsilon_greedy(nextstate,epsilon)
#we calculate Q value of the previous state using our update rule
Q[(state,action)] += alpha * (reward + gamma * Q[(nextstate,nextaction)]-Q[(state,action)])
#finally we update our state and action with next action
#and next state
action = nextaction
state = nextstate
r += reward
#we will break the loop, if we are at the terminal
#state of the episode
if done:
break
env.close()
Q 学习和 SARSA 之间的区别
Q 学习和 SARSA 对许多人来说总是很困惑。 让我们分解一下两者之间的差异。 在此处查看流程图:
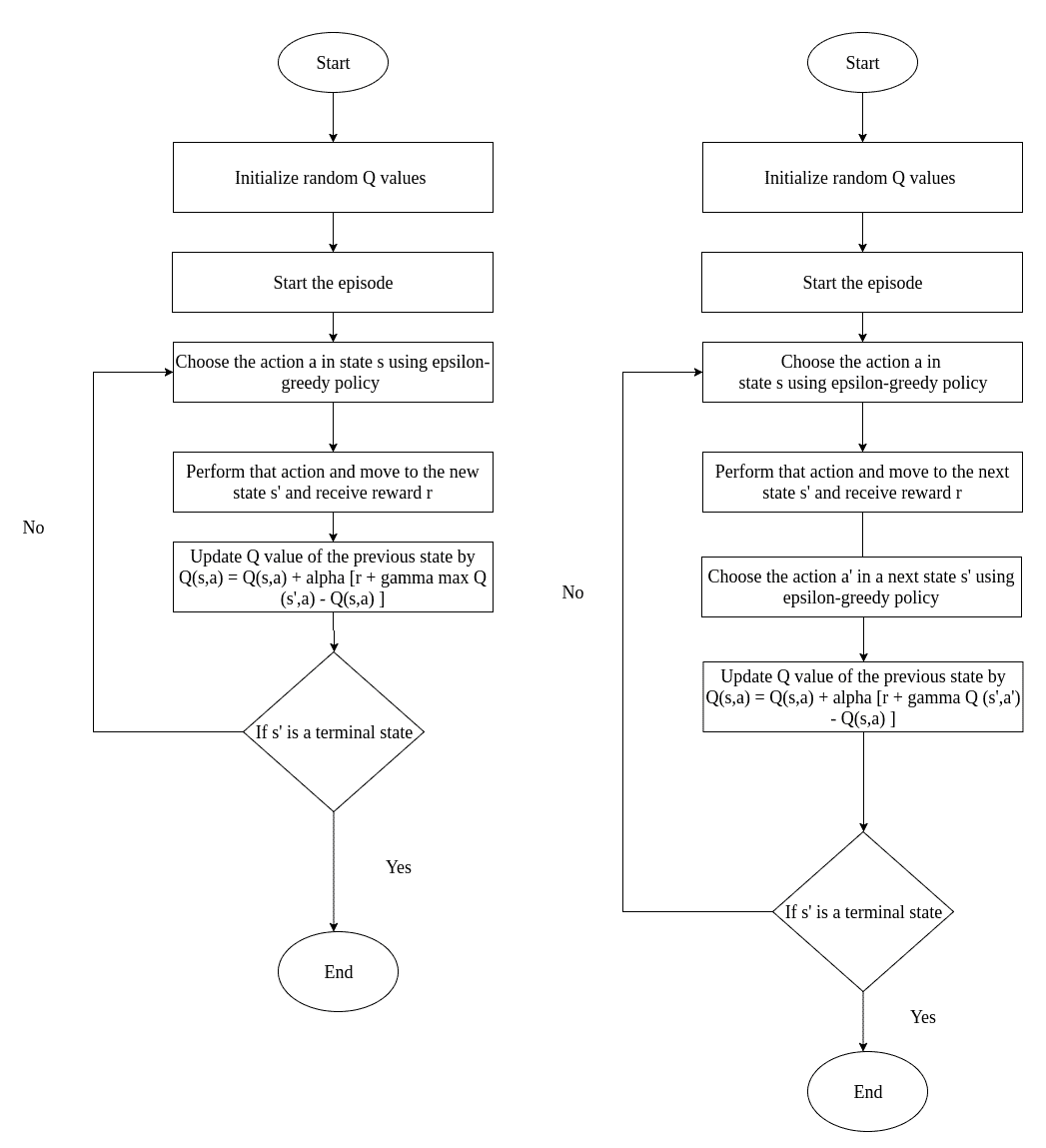
您看得出来差别吗? 在 Q 学习中,我们使用ε贪婪策略采取行动,并且在更新 Q 值的同时,我们仅采取最大行动。 在 SARSA 中,我们使用ε贪婪策略采取措施,并且在更新 Q 值的同时,我们使用ε贪婪策略采取措施。
总结
在本章中,我们学习了一种克服了蒙特卡洛方法局限性的不同的无模型学习算法。 我们看到了预测和控制方法。 在 TD 预测中,我们根据下一个状态更新了状态的状态值。 在控制方法方面,我们看到了两种不同的算法:Q 学习和 SARSA。
问题
问题列表如下:
- TD 学习与蒙特卡洛方法有何不同?
- TD 误差到底是什么?
- TD 预测和控制之间有什么区别?
- 如何使用 Q 学习构建智能体?
- Q 学习和 SARSA 有什么区别?