原文：Hands-On Reinforcement Learning with Python
译者：飞龙
本文来自【ApacheCN 深度学习 译文集】，采用译后编辑（MTPE）流程来尽可能提升效率。
不要担心自己的形象，只关心如何实现目标。——《原则》，生活原则 2.3.c
十一、策略梯度和优化
在最后三章中，我们学习了各种深度强化学习算法，例如深度 Q 网络（DQN），深度循环 Q 网络（DRQN）和异步优势演员评论家（A3C）网络。 在所有算法中，我们的目标是找到正确的策略，以便我们能够最大化回报。 我们使用 Q 函数来找到最佳策略，因为 Q 函数告诉我们哪个动作是在某种状态下执行的最佳动作。 您认为我们不使用 Q 函数就能直接找到最优策略吗？ 是。 我们可以。 在策略梯度方法中，我们无需使用 Q 函数就可以找到最优策略。
在本章中，我们将详细了解策略梯度。 我们还将研究不同类型的策略梯度方法，例如深度确定性策略梯度，然后是最新的策略优化方法，例如信任区域策略优化和近端策略优化。
在本章中，您将学习以下内容：
- 策略梯度
- 使用策略梯度的 Lunar Lander
- 深度确定性策略梯度
- 使用深度确定性策略梯度（DDPG）摆动
- 信任区域策略优化
- 近端策略优化
策略梯度
策略梯度是强化学习（RL）的惊人算法之一，在该算法中，我们直接优化由某些参数θ设置的策略。 到目前为止，我们已经使用 Q 函数来找到最佳策略。 现在，我们将了解如何找到没有 Q 函数的最优策略。 首先，让我们将策略函数定义为π(a | s)，即在状态为s的情况下采取a动作的概率。 我们通过参数θ将策略参数化为π(a | s; θ)，这使我们能够确定状态下的最佳操作。
策略梯度方法具有多个优点，它可以处理连续动作空间，在该连续动作空间中，我们具有无限数量的动作和状态。 假设我们正在制造自动驾驶汽车。 驾驶汽车时应避免撞到其他车辆。 当汽车撞到车辆时，我们得到负奖励，而当汽车没有撞到其他车辆时，我们得到正奖励。 我们以仅获得积极奖励的方式更新模型参数，以使我们的汽车不会撞到任何其他车辆。 这是策略梯度的基本思想：我们以最大化报酬的方式更新模型参数。 让我们详细看一下。
我们使用神经网络来找到最佳策略，我们将此网络称为策略网络。 策略网络的输入将是状态，而输出将是该状态中每个操作的概率。 一旦有了这个概率，就可以从该分布中采样一个动作，并在状态下执行该动作。 但是我们采样的动作可能不是在该状态下执行的正确动作。 很好-我们执行动作并存储奖励。 同样，我们通过从分布中采样一个动作来在每种状态下执行动作，并存储奖励。 现在，这成为我们的训练数据。 我们执行梯度下降并以这样的方式更新梯度：在状态下产生高奖励的动作将具有较高的概率，而在状态下产生低奖励的动作将具有较低的概率。 什么是损失函数？ 在这里，我们使用 softmax 交叉熵损失，然后将损失乘以奖励值。
使用策略梯度的 Lunar Lander
假设我们的经纪人正在驾驶航天器，而我们的经纪人的目标是正确着陆在着陆垫上。 如果我们的智能体（着陆器）从着陆点着陆，则它会失去奖励，并且如果智能体崩溃或休息，剧集将终止。 在环境中可用的四个离散动作是“不执行任何操作”，“点火向左的引擎”，“点火主引擎”和“点火向右的引擎”。
现在，我们将看到如何训练我们的智能体以策略梯度正确降落在降落区。 本节中使用的代码属于 Gabriel：
首先，我们导入必要的库：
import tensorflow as tf
import numpy as np
from tensorflow.python.framework import ops
import gym
import numpy as np
import time
然后，我们定义PolicyGradient类，该类实现了策略梯度算法。 让我们分解类并分别查看每个函数。 您可以将整个程序看作 Jupyter 笔记本：
class PolicyGradient:
# first we define the __init__ method where we initialize all variables
def __init__(self, n_x,n_y,learning_rate=0.01, reward_decay=0.95):
# number of states in the environment
self.n_x = n_x
# number of actions in the environment
self.n_y = n_y
# learning rate of the network
self.lr = learning_rate
# discount factor
self.gamma = reward_decay
# initialize the lists for storing observations,
# actions and rewards
self.episode_observations, self.episode_actions, self.episode_rewards = [], [], []
# we define a function called build_network for
# building the neural network
self.build_network()
# stores the cost i.e loss
self.cost_history = []
# initialize tensorflow session
self.sess = tf.Session()
self.sess.run(tf.global_variables_initializer())
接下来，我们定义一个store_transition函数，该函数存储转换，即state，action和reward。 我们可以使用以下信息来训练网络：
def store_transition(self, s, a, r):
self.episode_observations.append(s)
self.episode_rewards.append(r)
# store actions as list of arrays
action = np.zeros(self.n_y)
action[a] = 1
self.episode_actions.append(action)
给定state，我们定义choose_action函数来选择action：
def choose_action(self, observation):
# reshape observation to (num_features, 1)
observation = observation[:, np.newaxis]
# run forward propagation to get softmax probabilities
prob_weights = self.sess.run(self.outputs_softmax, feed_dict = {self.X: observation})
# select action using a biased sample this will return
# the index of the action we have sampled
action = np.random.choice(range(len(prob_weights.ravel())), p=prob_weights.ravel())
return action
我们定义用于构建神经网络的build_network函数：
def build_network(self):
# placeholders for input x, and output y
self.X = tf.placeholder(tf.float32, shape=(self.n_x, None), name="X")
self.Y = tf.placeholder(tf.float32, shape=(self.n_y, None), name="Y")
# placeholder for reward
self.discounted_episode_rewards_norm = tf.placeholder(tf.float32, [None, ], name="actions_value")
# we build 3 layer neural network with 2 hidden layers and
# 1 output layer
# number of neurons in the hidden layer
units_layer_1 = 10
units_layer_2 = 10
# number of neurons in the output layer
units_output_layer = self.n_y
# now let us initialize weights and bias value using
# tensorflow's tf.contrib.layers.xavier_initializer
W1 = tf.get_variable("W1", [units_layer_1, self.n_x], initializer = tf.contrib.layers.xavier_initializer(seed=1))
b1 = tf.get_variable("b1", [units_layer_1, 1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
W2 = tf.get_variable("W2", [units_layer_2, units_layer_1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
b2 = tf.get_variable("b2", [units_layer_2, 1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
W3 = tf.get_variable("W3", [self.n_y, units_layer_2], initializer = tf.contrib.layers.xavier_initializer(seed=1))
b3 = tf.get_variable("b3", [self.n_y, 1], initializer = tf.contrib.layers.xavier_initializer(seed=1))
# and then, we perform forward propagation
Z1 = tf.add(tf.matmul(W1,self.X), b1)
A1 = tf.nn.relu(Z1)
Z2 = tf.add(tf.matmul(W2, A1), b2)
A2 = tf.nn.relu(Z2)
Z3 = tf.add(tf.matmul(W3, A2), b3)
A3 = tf.nn.softmax(Z3)
# as we require, probabilities, we apply softmax activation
# function in the output layer,
logits = tf.transpose(Z3)
labels = tf.transpose(self.Y)
self.outputs_softmax = tf.nn.softmax(logits, name='A3')
# next we define our loss function as cross entropy loss
neg_log_prob = tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels)
# reward guided loss
loss = tf.reduce_mean(neg_log_prob * self.discounted_episode_rewards_norm)
# we use adam optimizer for minimizing the loss
self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)
接下来，我们定义discount_and_norm_rewards函数，该函数将导致折扣和标准化奖励：
def discount_and_norm_rewards(self):
discounted_episode_rewards = np.zeros_like(self.episode_rewards)
cumulative = 0
for t in reversed(range(len(self.episode_rewards))):
cumulative = cumulative * self.gamma + self.episode_rewards[t]
discounted_episode_rewards[t] = cumulative
discounted_episode_rewards -= np.mean(discounted_episode_rewards)
discounted_episode_rewards /= np.std(discounted_episode_rewards)
return discounted_episode_rewards
现在我们实际执行学习：
def learn(self):
# discount and normalize episodic reward
discounted_episode_rewards_norm = self.discount_and_norm_rewards()
# train the network
self.sess.run(self.train_op, feed_dict={
self.X: np.vstack(self.episode_observations).T,
self.Y: np.vstack(np.array(self.episode_actions)).T,
self.discounted_episode_rewards_norm: discounted_episode_rewards_norm,
})
# reset the episodic data
self.episode_observations, self.episode_actions, self.episode_rewards = [], [], []
return discounted_episode_rewards_norm
您可以看到如下输出：
深度确定性策略梯度
在第 8 章，“深度 Q 网络和 Atari 游戏”中，我们研究了 DQN 的工作原理，并应用了 DQN 玩 Atari 游戏。 但是，在那些离散的环境中，我们只有一组有限的动作。 想象一个连续的环境空间，例如训练机器人走路； 在那些环境中，应用 Q 学习是不可行的，因为要找到一个贪婪的策略将需要在每一步进行很多优化。 即使我们使连续的环境离散，我们也可能会失去重要的函数并最终获得大量的动作空间。 当我们拥有巨大的行动空间时，很难实现融合。
因此，我们使用称为演员评论家的新架构，该架构具有两个网络：演员和评论家。 演员评论家架构结合了策略梯度和状态操作值函数。 演员网络的作用是通过调整参数θ来确定状态中的最佳动作，而评论家的作用是评估演员产生的动作。 评论家通过计算时间差异误差来评估演员的行动。 也就是说，我们在演员网络上执行策略梯度以选择操作， 评论家网络使用 TD 误差评估由演员网络产生的操作。 下图显示了演员评论家架构：
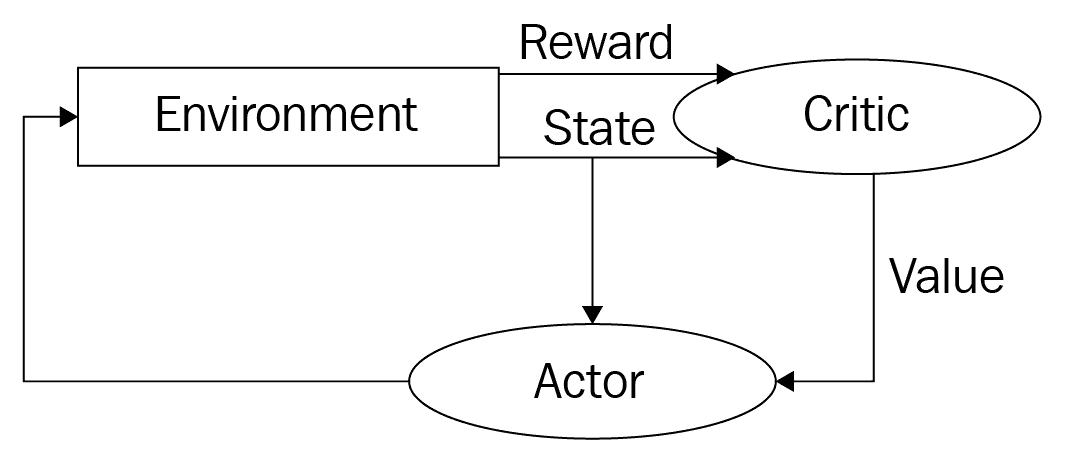
与 DQN 相似，这里我们使用经验缓冲区，通过采样少量的经验来训练演员和评论家网络。 我们还使用单独的目标演员和评论家网络来计算损失。
例如，在乒乓游戏中，我们将具有不同比例的不同特征，例如位置，速度等。 因此，我们以所有特征都处于相同比例的方式来缩放特征。 我们使用一种称为批归一化的方法来缩放特征。 它将所有特征归一化以具有单位均值和方差。 我们如何探索新的行动？ 在连续环境中，将有n个动作。 为了探索新动作，我们在演员网络产生的动作中添加了一些噪声N。 我们使用称为 Ornstein-Uhlenbeck 随机过程的过程来生成此噪声。
现在，我们将详细介绍 DDPG 算法。
假设我们有两个网络：演员网络和评论家网络。 我们用输入为状态的μ(s; θ^μ)表示演员网络
，并以θ^μ作为演员网络权重的结果进行操作。 我们将评论家网络表示为Q(s, a; θ^Q)，它将输入作为状态和动作并返回Q值，其中θ^Q是评论家网络权重。
同样，我们将演员网络和评论家网络的目标网络分别定义为μ(s; θ^μ')和Q(s, a; θ^Q')，其中θ^μ'和θ^Q'是目标演员和评论家网络的权重。
我们使用策略梯度更新演员网络权重，并使用根据 TD 误差计算得出的梯度更新评论家网络权重。
首先，我们通过将探索噪声N添加到演员网络产生的动作（例如μ(s; θ^μ) + N）来选择动作。 我们在s状态下执行此操作，获得r奖励，然后移至新状态s'。 我们将此转移信息存储在经验回放缓冲区中。
经过一些迭代后，我们从回放缓冲区采样转移并训练网络，然后计算目标Q值：
我们将 TD 误差计算为：
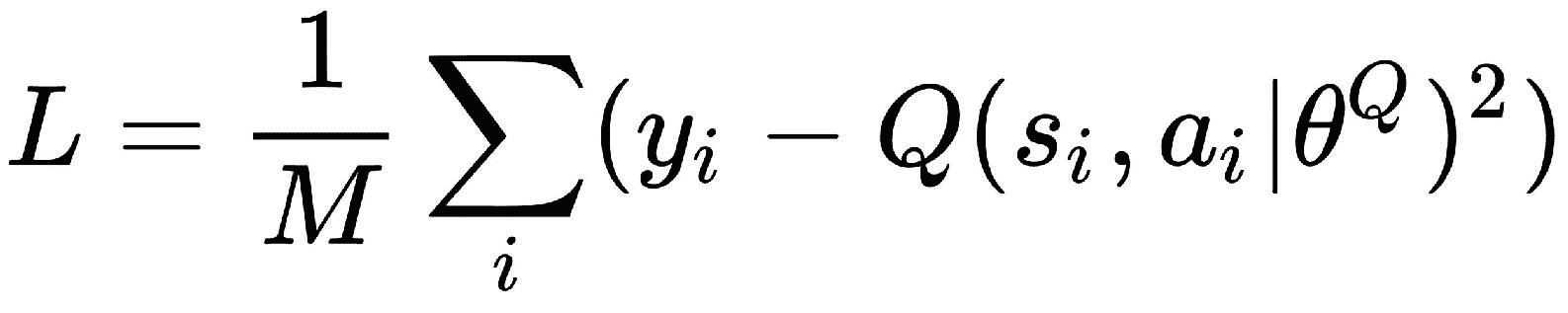
其中M是来自回放缓冲区的用于训练的样本数。 我们使用根据此损失L计算出的梯度来更新评论家网络的权重。
同样，我们使用策略梯度更新策略网络权重。 然后，我们在目标网络中更新 Actor 和评论家网络的权重。 我们会缓慢更新目标网络的权重，从而提高稳定性。 它称为软替换：
摆动摆锤
我们有一个从随机位置开始的摆锤，我们的探员的目标是向上摆动摆锤使其保持直立。 我们将在这里看到如何使用 DDPG。 wshuail 提供了本节中使用的代码。
首先，让我们导入必要的库：
import tensorflow as tf
import numpy as np
import gym
接下来，我们按如下方式定义超参数：
# number of steps in each episode
epsiode_steps = 500
# learning rate for actor
lr_a = 0.001
# learning rate for critic
lr_c = 0.002
# discount factor
gamma = 0.9
# soft replacement
alpha = 0.01
# replay buffer size
memory = 10000
# batch size for training
batch_size = 32
render = False
我们将在DDPG类中实现 DDPG 算法。 我们分解类以查看每个函数。 首先，我们初始化所有内容：
class DDPG(object):
def __init__(self, no_of_actions, no_of_states, a_bound,):
# initialize the memory with shape as no of actions, no of states and our defined memory size
self.memory = np.zeros((memory, no_of_states * 2 + no_of_actions + 1), dtype=np.float32)
# initialize pointer to point to our experience buffer
self.pointer = 0
# initialize tensorflow session
self.sess = tf.Session()
# initialize the variance for OU process for exploring policies
self.noise_variance = 3.0
self.no_of_actions, self.no_of_states, self.a_bound = no_of_actions, no_of_states, a_bound,
# placeholder for current state, next state and rewards
self.state = tf.placeholder(tf.float32, [None, no_of_states], 's')
self.next_state = tf.placeholder(tf.float32, [None, no_of_states], 's_')
self.reward = tf.placeholder(tf.float32, [None, 1], 'r')
# build the actor network which has separate eval(primary)
# and target network
with tf.variable_scope('Actor'):
self.a = self.build_actor_network(self.state, scope='eval', trainable=True)
a_ = self.build_actor_network(self.next_state, scope='target', trainable=False)
# build the critic network which has separate eval(primary)
# and target network
with tf.variable_scope('Critic'):
q = self.build_crtic_network(self.state, self.a, scope='eval', trainable=True)
q_ = self.build_crtic_network(self.next_state, a_, scope='target', trainable=False)
# initialize the network parameters
self.ae_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Actor/eval')
self.at_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Actor/target')
self.ce_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/eval')
self.ct_params = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope='Critic/target')
# update target value
self.soft_replace = [[tf.assign(at, (1-alpha)*at+alpha*ae), tf.assign(ct, (1-alpha)*ct+alpha*ce)]
for at, ae, ct, ce in zip(self.at_params, self.ae_params, self.ct_params, self.ce_params)]
# compute target Q value, we know that Q(s,a) = reward + gamma *
Q'(s',a')
q_target = self.reward + gamma * q_
# compute TD error i.e actual - predicted values
td_error = tf.losses.mean_squared_error(labels=(self.reward + gamma * q_), predictions=q)
# train the critic network with adam optimizer
self.ctrain = tf.train.AdamOptimizer(lr_c).minimize(td_error, name="adam-ink", var_list = self.ce_params)
# compute the loss in actor network
a_loss = - tf.reduce_mean(q)
# train the actor network with adam optimizer for
# minimizing the loss
self.atrain = tf.train.AdamOptimizer(lr_a).minimize(a_loss, var_list=self.ae_params)
# initialize summary writer to visualize our network in tensorboard
tf.summary.FileWriter("logs", self.sess.graph)
# initialize all variables
self.sess.run(tf.global_variables_initializer())
我们如何在 DDPG 中选择一个动作？ 我们通过向动作空间添加噪音来选择动作。 我们使用 Ornstein-Uhlenbeck 随机过程生成噪声：
def choose_action(self, s):
a = self.sess.run(self.a, {self.state: s[np.newaxis, :]})[0]
a = np.clip(np.random.normal(a, self.noise_variance), -2, 2)
return a
然后，我们定义learn函数，在该函数中进行实际训练。 在这里，我们从经验缓冲区中选择一批states，actions，rewards和下一个状态。 我们以此来训练演员和评论家网络：
def learn(self):
# soft target replacement
self.sess.run(self.soft_replace)
indices = np.random.choice(memory, size=batch_size)
batch_transition = self.memory[indices, :]
batch_states = batch_transition[:, :self.no_of_states]
batch_actions = batch_transition[:, self.no_of_states: self.no_of_states + self.no_of_actions]
batch_rewards = batch_transition[:, -self.no_of_states - 1: -self.no_of_states]
batch_next_state = batch_transition[:, -self.no_of_states:]
self.sess.run(self.atrain, {self.state: batch_states})
self.sess.run(self.ctrain, {self.state: batch_states, self.a: batch_actions, self.reward: batch_rewards, self.next_state: batch_next_state})
我们定义了一个store_transition函数，该函数将所有信息存储在缓冲区中并执行学习：
def store_transition(self, s, a, r, s_):
trans = np.hstack((s,a,[r],s_))
index = self.pointer % memory
self.memory[index, :] = trans
self.pointer += 1
if self.pointer > memory:
self.noise_variance *= 0.99995
self.learn()
我们定义了build_actor_network函数来构建演员网络：
def build_actor_network(self, s, scope, trainable):
# Actor DPG
with tf.variable_scope(scope):
l1 = tf.layers.dense(s, 30, activation = tf.nn.tanh, name = 'l1', trainable = trainable)
a = tf.layers.dense(l1, self.no_of_actions, activation = tf.nn.tanh, name = 'a', trainable = trainable)
return tf.multiply(a, self.a_bound, name = "scaled_a")
我们定义build_ crtic_network函数：
def build_crtic_network(self, s, a, scope, trainable):
# Critic Q-leaning
with tf.variable_scope(scope):
n_l1 = 30
w1_s = tf.get_variable('w1_s', [self.no_of_states, n_l1], trainable = trainable)
w1_a = tf.get_variable('w1_a', [self.no_of_actions, n_l1], trainable = trainable)
b1 = tf.get_variable('b1', [1, n_l1], trainable = trainable)
net = tf.nn.tanh( tf.matmul(s, w1_s) + tf.matmul(a, w1_a) + b1 )
q = tf.layers.dense(net, 1, trainable = trainable)
return q
现在，我们使用make函数初始化gym环境：
env = gym.make("Pendulum-v0")
env = env.unwrapped
env.seed(1)
我们得到状态数：
no_of_states = env.observation_space.shape[0]
我们得到的动作数：
no_of_actions = env.action_space.shape[0]
此外，该动作的上限：
a_bound = env.action_space.high
现在，我们为DDPG类创建一个对象：
ddpg = DDPG(no_of_actions, no_of_states, a_bound)
我们初始化列表以存储总奖励：
total_reward = []
设置剧集数：
no_of_episodes = 300
现在，让我们开始训练：
# for each episodes
for i in range(no_of_episodes):
# initialize the environment
s = env.reset()
# episodic reward
ep_reward = 0
for j in range(epsiode_steps):
env.render()
# select action by adding noise through OU process
a = ddpg.choose_action(s)
# perform the action and move to the next state s
s_, r, done, info = env.step(a)
# store the the transition to our experience buffer
# sample some minibatch of experience and train the network
ddpg.store_transition(s, a, r, s_)
# update current state as next state
s = s_
# add episodic rewards
ep_reward += r
if j == epsiode_steps-1:
# store the total rewards
total_reward.append(ep_reward)
# print rewards obtained per each episode
print('Episode:', i, ' Reward: %i' % int(ep_reward))
break
您将看到如下输出：
我们可以在 TensorBoard 中看到计算图：
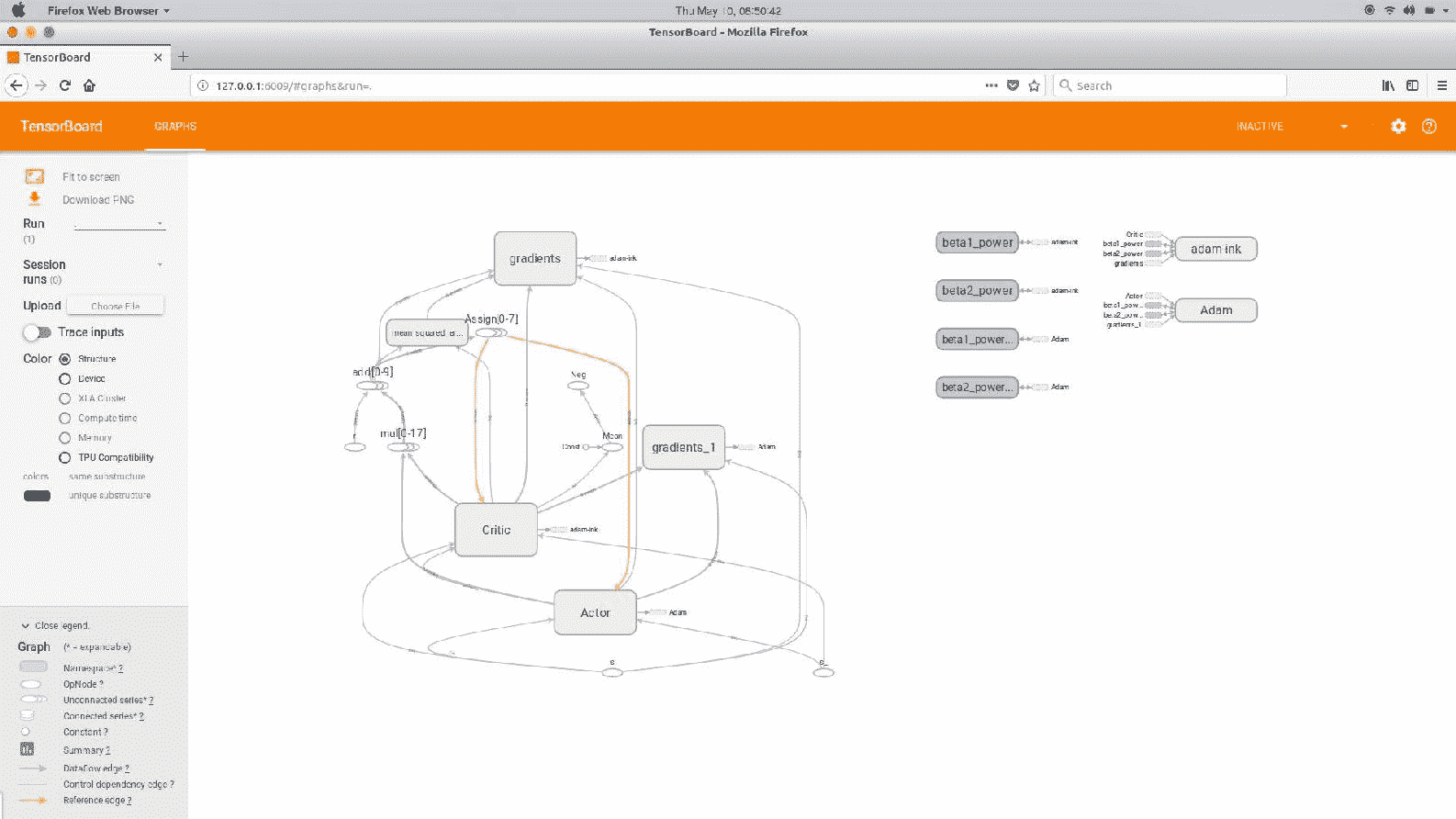
信任区域策略优化
在了解信任区域策略优化（TRPO）之前，我们需要了解受约束的策略优化。 我们知道，在 RL 智能体中，通过反复试验来学习，以使报酬最大化。 为了找到最佳策略，我们的智能体将探索所有不同的行动，并选择能获得良好回报的行动。 在探索不同的动作时，我们的智能体很有可能也会探索不良的动作。 但是最大的挑战是，当我们允许智能体在现实世界中学习以及奖励函数设计不当时。 例如，考虑一个学习走路而没有遇到任何障碍的智能体。 如果智能体被任何障碍物击中，它将获得负奖励；而如果没有被任何障碍物击中，则将获得正奖励。 为了找出最佳策略，智能体会探索不同的操作。 智能体还采取行动，例如撞到障碍物以检查它是否给出了良好的回报。 但这对我们的经纪人来说并不安全； 当智能体在现实环境中学习时，这尤其不安全。 因此，我们介绍了基于约束的学习。 我们设置一个阈值，如果碰到障碍物的可能性小于该阈值，则我们认为我们的智能体是安全的，否则我们认为我们的智能体是不安全的。 添加了约束以确保我们的智能体位于安全区域内。
在 TRPO 中，我们迭代地改进了该策略，并施加了一个约束，以使旧策略和新策略之间的 Kullback-Leibler（KL）差异要小于某个常数。 
。 该约束称为信任区域约束。
那么什么是 KL 散度？ KL 散度告诉我们两个概率分布如何彼此不同。 由于我们的策略是针对行动的概率分布，因此 KL 差异告诉我们新策略与旧策略有多远。 为什么我们必须使旧策略和新策略之间的距离保持小于恒定值δ？ 因为我们不希望我们的新策略与旧策略脱节。 因此，我们施加了约束以使新策略接近旧策略。 同样，为什么我们必须保持旧策略呢？ 当新策略与旧策略相距甚远时，它将影响智能体的学习表现，并导致完全不同的学习行为。 简而言之，在 TRPO 中，我们朝着改善策略的方向迈出了一步，即使报酬最大化，但我们还应确保满足信任区域约束。 它使用共轭梯度下降优化网络参数θ，同时满足约束条件。 该算法保证了单调策略的改进，并且在各种连续环境中也取得了出色的效果。
现在，我们将了解 TRPO 的数学原理。 如果您对数学不感兴趣，可以跳过本节。
准备一些很棒的数学。
让我们指定预期的总折扣奖励η(π)，如下所示：
现在让我们将新策略视为π'； 就相对于旧策略π的优势而言，可以将其定义为策略π'的预期回报，如下所示：
好吧，为什么我们要利用旧策略的优势？ 因为我们正在衡量新策略π'相对于旧策略π的平均效果有多好。 我们可以用状态之和而不是时间步来重写前面的方程，如下所示：
是折扣的访问频率，即：
如果您看到前面的方程η(π')，则ρ[π'](s)与π'
之间存在复杂的依存关系，因此很难对方程进行优化。 因此，我们将局部近似L[π](π')引入η(π')，如下所示：
使用访问频率ρ[π]而不是ρ[π']，也就是说，由于策略的变化，我们忽略了状态访问频率的变化。 简而言之，我们假设新旧策略的状态访问频率均相同。 当我们计算L[π]的梯度时，相对于某些参数θ而言，这也会提高η，我们不确定要采取多少步骤。
Kakade 和 Langford 提出了一种新的策略更新方法，称为保守策略迭代，如下所示：
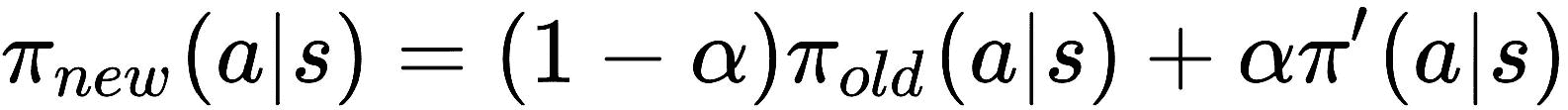----（1）
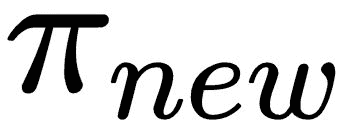是新策略。 π_old是旧策略。
，即π'，是最大化L[π_old]的策略。
Kakade 和 Langford 从(1)得出以下方程式：
----（2）
C是惩罚系数，等于4εγ / (1 - α)^2，D_max[KL]表示旧策略与新策略之间的 KL 散度。
如果我们仔细观察前面的方程式(2)，我们会注意到，只要右侧最大化，我们的预期长期回报η就会单调增加。
让我们将此右侧项定义为M[i](π)，如下所示：
----（3）
将公式(3)代入(2)，我们得到：
----（4）
由于我们知道两个相同策略之间的 KL 差异为0，我们可以这样写：
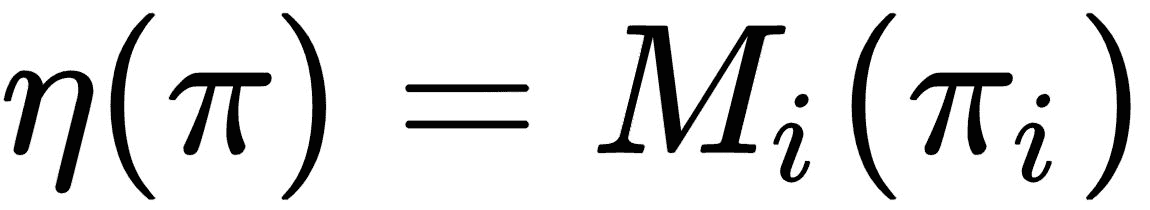----（5）
结合方程式(4)和(5)，我们可以写：
在前面的等式中，我们可以理解，最大化M[i]可以保证我们期望收益的最大化。 因此，现在我们的目标是最大化M[i]，从而最大化我们的预期回报。 由于我们使用参数化策略，因此在上一个公式中将π替换为θ，然后使用θ_old表示我们要改进的策略，如下所示：
但是，在前面的公式中具有惩罚系数C将导致步长非常小，从而减慢了更新速度。 因此，我们对 KL 散度的旧策略和新策略施加了约束，即信任区域约束，这将有助于我们找到最佳步长：
现在，问题是在状态空间的每个点上都施加了 KL 散度，当我们拥有高维状态空间时，解决它确实是不可行的。 因此，我们使用启发式近似，其平均 KL 散度为：
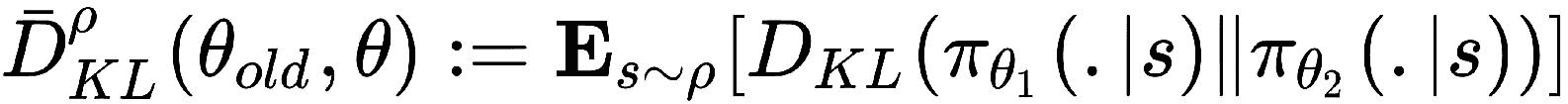
因此，现在，我们可以将平均 KL 散度约束重写为先前的目标函数，如下所示：
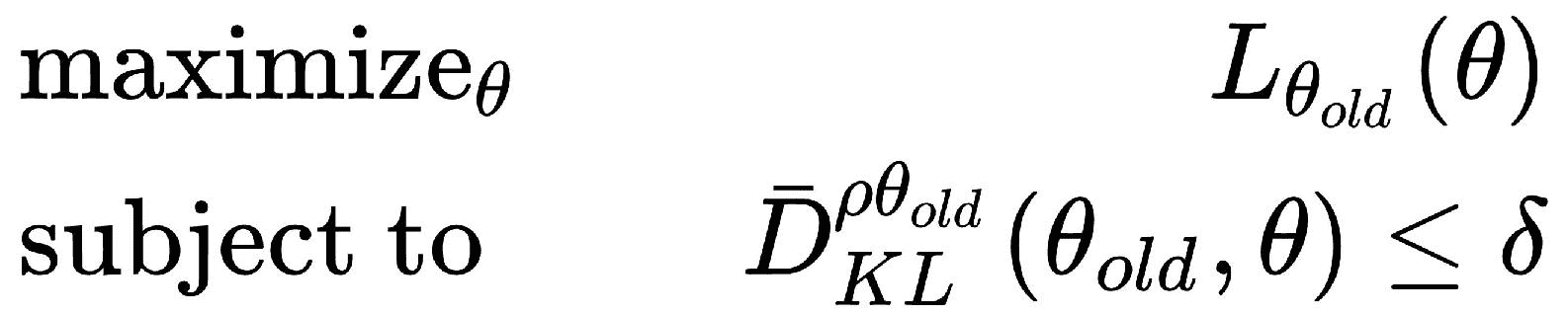
扩展L的值，我们得到以下信息：
在前面的公式中，我们将状态总和Σ[s] ρ θ_old替换为期望E[s ~ ρ θ_old]，并且将重要性总和估计值替换为行动总和，如下所示：
然后，我们将优势目标值A[θ_old]替换为 Q 值Q[θ_old]。
因此，我们最终的目标函数将变为：
优化前面提到的具有约束的目标函数称为约束优化。 我们的约束是使旧策略和新策略之间的平均 KL 差异小于δ。我们使用共轭梯度下降来优化先前的函数。
近端策略优化
现在，我们将看另一种策略优化算法，称为近端策略优化（PPO）。 它是对 TRPO 的改进，由于其表现，已成为解决许多复杂 RL 问题的默认 RL 算法。 它是 OpenAI 的研究人员为克服 TRPO 的缺点而提出的。 回忆一下 TRPO 的替代目标函数。 这是一个约束优化问题，我们在其中施加了一个约束-新旧策略之间的平均 KL 差异应小于δ。 但是 TRPO 的问题在于，它需要大量计算能力才能计算共轭梯度以执行约束优化。
因此，PPO 通过将约束更改为惩罚项来修改 TRPO 的目标函数，因此我们不想执行共轭梯度。 现在，让我们看看 PPO 的工作原理。 我们将r[t](θ)定义为新旧策略之间的概率比。 因此，我们可以将目标函数编写为：
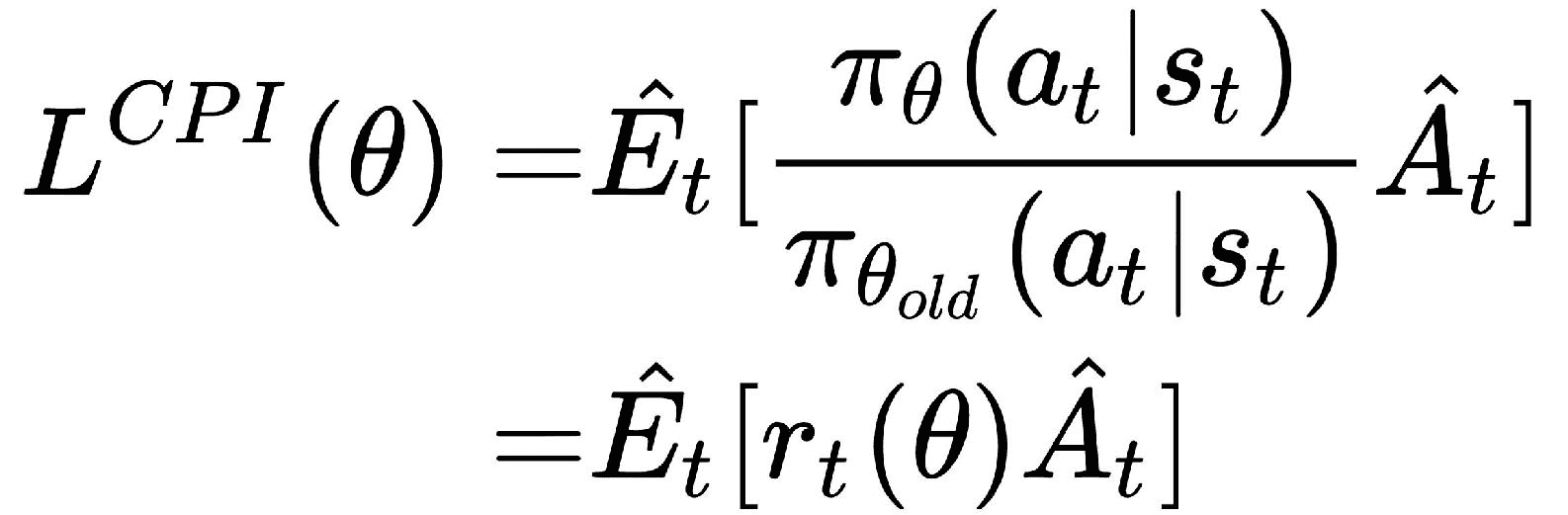
L_CPI表示保守策略迭代。 但是最大化L会导致无限制地进行大量策略更新。 因此，我们通过添加惩罚项来重新定义我们的目标函数，该惩罚项会惩罚较大的策略更新。 现在目标函数变为：
我们刚刚在实际方程式中添加了一个新项：
这是什么意思？ 实际上，它会在间隔[1 - ε, 1 + ε]之间裁剪r[t](θ)的值，也就是说，如果r[t](θ)的值导致目标函数增加，则在间隔之间大量裁剪的值会降低其效果。
基于两种情况，我们将概率比限制在1 - ε或ε：
- 案例 1：
A_hat[t] > 0
当优势为正时，这意味着相对于所有其他操作的平均值，应优先选择相应的操作。 我们将为该操作增加r[t](θ)的值，因此将有更大的机会被选择。 当我们执行r[t](θ)的限幅值时，不会超过1 + ε：
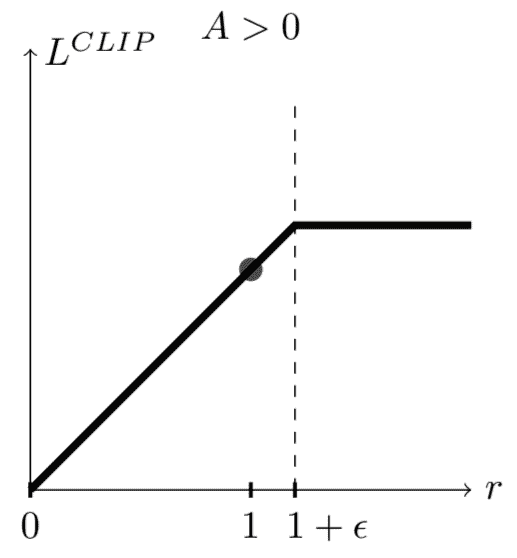
- 案例 2：
A_hat[t]
当优势的值为负时，这意味着该动作没有意义，因此不应采用。 因此，在这种情况下，我们将减小该操作的r[t](θ)值，以使其被选择的机会较小。 类似地，当我们执行裁剪时，r[t](θ)的值将不会减小到小于1 - ε：
当我们使用神经网络架构时，我们必须定义损失函数，其中包括目标函数的值函数误差。 就像在 A3C 中一样，我们还将添加熵损失以确保足够的探索。 因此，我们最终的目标函数变为：
c[1]和c[2]是系数，L[t]^(VP)是实际值和目标值函数之间的平方误差损失，即：
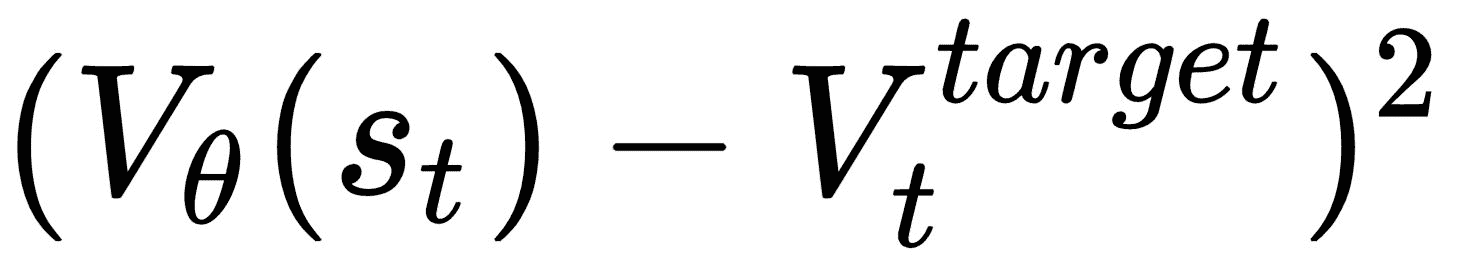
S是熵增。
总结
我们从策略梯度方法开始，该方法无需 Q 函数即可直接优化策略。 我们通过解决 Lunar Lander 游戏了解了策略梯度，并研究了 DDPG，它具有策略梯度和 Q 函数的优点。
然后，我们研究了诸如 TRPO 之类的策略优化算法，该算法通过对新旧策略之间的 KL 差异实现不大于δ的限制来确保单调策略的改进。
我们还研究了近端策略优化，该优化通过惩罚大型策略更新将约束变为惩罚。 在下一章第 12 章， “Capstone 项目 – 使用 DQN 进行赛车”，我们将了解如何构建能够赢得赛车游戏的智能体。
问题
问题列表如下：
- 什么是策略梯度？
- 策略梯度为何有效？
- DDPG 中的演员评论家网络有什么用途？
- 约束优化问题是什么？
- 什么是信任区域？
- PPO 如何克服 TRPO 的缺点？
进一步阅读
您可以进一步参考以下论文：
十二、Capstone 项目 – 将 DQN 用于赛车
在最后几章中，我们通过使用神经网络近似 q 函数来了解 Deep Q 学习的工作原理。 在此之后，我们看到了深度 Q 网络（DQN）的各种改进，例如双重 Q 学习，决斗网络架构和深度循环 Q 网络。 我们已经了解了 DQN 如何利用回放缓冲区来存储智能体的经验，并使用缓冲区中的小批样本来训练网络。 我们还实现了用于玩 Atari 游戏的 DQN 和一个用于玩 Doom 游戏的深度循环 Q 网络（DRQN）。 在本章中，让我们进入决斗 DQN 的详细实现，它与常规 DQN 基本相同，除了最终的全连接层将分解为两个流，即值流和优势流，而这两个流将合并在一起以计算 Q 函数。 我们将看到如何训练决斗的 DQN 来赢得赛车比赛的智能体。
在本章中，您将学习如何实现以下内容：
- 环境包装器函数
- 决斗网络
- 回放缓冲区
- 训练网络
- 赛车
环境包装器函数
本章使用的代码归功于 Giacomo Spigler 的 GitHub 存储库。 在本章中，每一行都对代码进行了说明。 有关完整的结构化代码，请查看上面的 GitHub 存储库。
首先，我们导入所有必需的库：
import numpy as np
import tensorflow as tf
import gym
from gym.spaces import Box
from scipy.misc import imresize
import random
import cv2
import time
import logging
import os
import sys
我们定义EnvWrapper类并定义一些环境包装器函数：
class EnvWrapper:
我们定义__init__方法并初始化变量：
def __init__(self, env_name, debug=False):
初始化gym环境：
self.env = gym.make(env_name)
获取action_space：
self.action_space = self.env.action_space
获取observation_space：
self.observation_space = Box(low=0, high=255, shape=(84, 84, 4))
初始化frame_num以存储帧数：
self.frame_num = 0
初始化monitor以记录游戏画面：
self.monitor = self.env.monitor
初始化frames：
self.frames = np.zeros((84, 84, 4), dtype=np.uint8)
初始化一个名为debug的布尔值，将其设置为true时将显示最后几帧：
self.debug = debug
if self.debug:
cv2.startWindowThread()
cv2.namedWindow("Game")
接下来，我们定义一个名为step的函数，该函数将当前状态作为输入并返回经过预处理的下一状态的帧：
def step(self, a):
ob, reward, done, xx = self.env.step(a)
return self.process_frame(ob), reward, done, xx
我们定义了一个称为reset的函数来重置环境； 重置后，它将返回预处理的游戏屏幕：
def reset(self):
self.frame_num = 0
return self.process_frame(self.env.reset())
接下来，我们定义另一个用于渲染环境的函数：
def render(self):
return self.env.render()
现在，我们定义用于预处理帧的process_frame函数：
def process_frame(self, frame):
# convert the image to gray
state_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
# change the size
state_resized = cv2.resize(state_gray,(84,110))
#resize
gray_final = state_resized[16:100,:]
if self.frame_num == 0:
self.frames[:, :, 0] = gray_final
self.frames[:, :, 1] = gray_final
self.frames[:, :, 2] = gray_final
self.frames[:, :, 3] = gray_final
else:
self.frames[:, :, 3] = self.frames[:, :, 2]
self.frames[:, :, 2] = self.frames[:, :, 1]
self.frames[:, :, 1] = self.frames[:, :, 0]
self.frames[:, :, 0] = gray_final
# Next we increment the frame_num counter
self.frame_num += 1
if self.debug:
cv2.imshow('Game', gray_final)
return self.frames.copy()
经过预处理后，我们的游戏屏幕如下图所示：
决斗网络
现在，我们构建决斗 DQN； 我们先构建三个卷积层，然后是两个全连接层，最后一个全连接层将被分为两个单独的层，用于值流和优势流。 我们将使用将值流和优势流结合在一起的聚合层来计算 q 值。 这些层的大小如下：
- 第 1 层：32 个
8x8过滤器，步幅为 4 + RELU - 第 2 层：64 个
4x4过滤器，步幅为 2 + RELU - 第 3 层：64 个
3x3过滤器，步幅为 1 + RELU - 第 4a 层：512 个单元的全连接层 + RELU
- 第 4b 层：512 个单元的全连接层 + RELU
- 第 5a 层：1 个 FC + RELU（状态值）
- 第 5b 层：动作 FC + RELU（优势值）
- 第 6 层：总计
V(s) + A(s, a)
class QNetworkDueling(QNetwork):
我们定义__init__方法来初始化所有层：
def __init__(self, input_size, output_size, name):
self.name = name
self.input_size = input_size
self.output_size = output_size
with tf.variable_scope(self.name):
# Three convolutional Layers
self.W_conv1 = self.weight_variable([8, 8, 4, 32])
self.B_conv1 = self.bias_variable([32])
self.stride1 = 4
self.W_conv2 = self.weight_variable([4, 4, 32, 64])
self.B_conv2 = self.bias_variable([64])
self.stride2 = 2
self.W_conv3 = self.weight_variable([3, 3, 64, 64])
self.B_conv3 = self.bias_variable([64])
self.stride3 = 1
# Two fully connected layer
self.W_fc4a = self.weight_variable([7`7`64, 512])
self.B_fc4a = self.bias_variable([512])
self.W_fc4b = self.weight_variable([7`7`64, 512])
self.B_fc4b = self.bias_variable([512])
# Value stream
self.W_fc5a = self.weight_variable([512, 1])
self.B_fc5a = self.bias_variable([1])
# Advantage stream
self.W_fc5b = self.weight_variable([512, self.output_size])
self.B_fc5b = self.bias_variable([self.output_size])
我们定义__call__方法并执行卷积运算：
def __call__(self, input_tensor):
if type(input_tensor) == list:
input_tensor = tf.concat(1, input_tensor)
with tf.variable_scope(self.name):
# Perform convolutional on three layers
self.h_conv1 = tf.nn.relu( tf.nn.conv2d(input_tensor, self.W_conv1, strides=[1, self.stride1, self.stride1, 1], padding='VALID') + self.B_conv1 )
self.h_conv2 = tf.nn.relu( tf.nn.conv2d(self.h_conv1, self.W_conv2, strides=[1, self.stride2, self.stride2, 1], padding='VALID') + self.B_conv2 )
self.h_conv3 = tf.nn.relu( tf.nn.conv2d(self.h_conv2, self.W_conv3, strides=[1, self.stride3, self.stride3, 1], padding='VALID') + self.B_conv3 )
# Flatten the convolutional output
self.h_conv3_flat = tf.reshape(self.h_conv3, [-1, 7`7`64])
# Fully connected layer
self.h_fc4a = tf.nn.relu(tf.matmul(self.h_conv3_flat, self.W_fc4a) + self.B_fc4a)
self.h_fc4b = tf.nn.relu(tf.matmul(self.h_conv3_flat, self.W_fc4b) + self.B_fc4b)
# Compute value stream and advantage stream
self.h_fc5a_value = tf.identity(tf.matmul(self.h_fc4a, self.W_fc5a) + self.B_fc5a)
self.h_fc5b_advantage = tf.identity(tf.matmul(self.h_fc4b, self.W_fc5b) + self.B_fc5b)
# Club both the value and advantage stream
self.h_fc6 = self.h_fc5a_value + ( self.h_fc5b_advantage - tf.reduce_mean(self.h_fc5b_advantage, reduction_indices=[1,], keep_dims=True) )
return self.h_fc6
回放记忆
现在，我们构建经验回放缓冲区，该缓冲区用于存储所有智能体的经验。 我们从回放缓冲区中抽取了少量经验来训练网络：
class ReplayMemoryFast:
首先，我们定义__init__方法并启动缓冲区大小：
def __init__(self, memory_size, minibatch_size):
# max number of samples to store
self.memory_size = memory_size
# minibatch size
self.minibatch_size = minibatch_size
self.experience = [None]*self.memory_size
self.current_index = 0
self.size = 0
接下来，我们定义store函数来存储经验：
def store(self, observation, action, reward, newobservation, is_terminal):
将经验存储为元组（当前状态action，reward，下一个状态是最终状态）：
self.experience[self.current_index] = (observation, action, reward, newobservation, is_terminal)
self.current_index += 1
self.size = min(self.size+1, self.memory_size)
如果索引大于内存，那么我们通过减去内存大小来刷新索引：
if self.current_index >= self.memory_size:
self.current_index -= self.memory_size
接下来，我们定义一个sample函数，用于对小批量经验进行采样：
def sample(self):
if self.size < self.minibatch_size:
return []
# First we randomly sample some indices
samples_index = np.floor(np.random.random((self.minibatch_size,))*self.size)
# select the experience from the sampled indexed
samples = [self.experience[int(i)] for i in samples_index]
return samples
训练网络
现在，我们将看到如何训练网络。
首先，我们定义DQN类并在__init__方法中初始化所有变量：
class DQN(object):
def __init__(self, state_size,
action_size,
session,
summary_writer = None,
exploration_period = 1000,
minibatch_size = 32,
discount_factor = 0.99,
experience_replay_buffer = 10000,
target_qnet_update_frequency = 10000,
initial_exploration_epsilon = 1.0,
final_exploration_epsilon = 0.05,
reward_clipping = -1,
):
初始化所有变量：
self.state_size = state_size
self.action_size = action_size
self.session = session
self.exploration_period = float(exploration_period)
self.minibatch_size = minibatch_size
self.discount_factor = tf.constant(discount_factor)
self.experience_replay_buffer = experience_replay_buffer
self.summary_writer = summary_writer
self.reward_clipping = reward_clipping
self.target_qnet_update_frequency = target_qnet_update_frequency
self.initial_exploration_epsilon = initial_exploration_epsilon
self.final_exploration_epsilon = final_exploration_epsilon
self.num_training_steps = 0
通过为我们的QNetworkDueling类创建实例来初始化主要决斗 DQN：
self.qnet = QNetworkDueling(self.state_size, self.action_size, "qnet")
同样，初始化目标决斗 DQN：
self.target_qnet = QNetworkDueling(self.state_size, self.action_size, "target_qnet")
接下来，将优化器初始化为RMSPropOptimizer：
self.qnet_optimizer = tf.train.RMSPropOptimizer(learning_rate=0.00025, decay=0.99, epsilon=0.01)
现在，通过为我们的ReplayMemoryFast类创建实例来初始化experience_replay_buffer：
self.experience_replay = ReplayMemoryFast(self.experience_replay_buffer, self.minibatch_size)
# Setup the computational graph
self.create_graph()
接下来，我们定义copy_to_target_network函数，用于将权重从主网络复制到目标网络：
def copy_to_target_network(source_network, target_network):
target_network_update = []
for v_source, v_target in zip(source_network.variables(), target_network.variables()):
# update target network
update_op = v_target.assign(v_source)
target_network_update.append(update_op)
return tf.group(*target_network_update)
现在，我们定义create_graph函数并构建我们的计算图：
def create_graph(self):
我们计算q_values并选择具有最大q值的动作：
with tf.name_scope("pick_action"):
# placeholder for state
self.state = tf.placeholder(tf.float32, (None,)+self.state_size , name="state")
# placeholder for q values
self.q_values = tf.identity(self.qnet(self.state) , name="q_values")
# placeholder for predicted actions
self.predicted_actions = tf.argmax(self.q_values, dimension=1 , name="predicted_actions")
# plot histogram to track max q values
tf.histogram_summary("Q values", tf.reduce_mean(tf.reduce_max(self.q_values, 1))) # save max q-values to track learning
接下来，我们计算目标未来奖励：
with tf.name_scope("estimating_future_rewards"):
self.next_state = tf.placeholder(tf.float32, (None,)+self.state_size , name="next_state")
self.next_state_mask = tf.placeholder(tf.float32, (None,) , name="next_state_mask")
self.rewards = tf.placeholder(tf.float32, (None,) , name="rewards")
self.next_q_values_targetqnet = tf.stop_gradient(self.target_qnet(self.next_state), name="next_q_values_targetqnet")
self.next_q_values_qnet = tf.stop_gradient(self.qnet(self.next_state), name="next_q_values_qnet")
self.next_selected_actions = tf.argmax(self.next_q_values_qnet, dimension=1)
self.next_selected_actions_onehot = tf.one_hot(indices=self.next_selected_actions, depth=self.action_size)
self.next_max_q_values = tf.stop_gradient( tf.reduce_sum( tf.mul( self.next_q_values_targetqnet, self.next_selected_actions_onehot ) , reduction_indices=[1,] ) * self.next_state_mask )
self.target_q_values = self.rewards + self.discount_factor*self.next_max_q_values
接下来，我们使用 RMSProp 优化器执行优化：
with tf.name_scope("optimization_step"):
self.action_mask = tf.placeholder(tf.float32, (None, self.action_size) , name="action_mask")
self.y = tf.reduce_sum( self.q_values * self.action_mask , reduction_indices=[1,])
## ERROR CLIPPING
self.error = tf.abs(self.y - self.target_q_values)
quadratic_part = tf.clip_by_value(self.error, 0.0, 1.0)
linear_part = self.error - quadratic_part
self.loss = tf.reduce_mean( 0.5*tf.square(quadratic_part) + linear_part )
# optimize the gradients
qnet_gradients = self.qnet_optimizer.compute_gradients(self.loss, self.qnet.variables())
for i, (grad, var) in enumerate(qnet_gradients):
if grad is not None:
qnet_gradients[i] = (tf.clip_by_norm(grad, 10), var)
self.qnet_optimize = self.qnet_optimizer.apply_gradients(qnet_gradients)
将主要网络权重复制到目标网络：
with tf.name_scope("target_network_update"):
self.hard_copy_to_target = DQN.copy_to_target_network(self.qnet, self.target_qnet)
我们定义了store函数，用于将所有经验存储在experience_replay_buffer中：
def store(self, state, action, reward, next_state, is_terminal):
# rewards clipping
if self.reward_clipping > 0.0:
reward = np.clip(reward, -self.reward_clipping, self.reward_clipping)
self.experience_replay.store(state, action, reward, next_state, is_terminal)
我们定义了一个action函数，用于使用衰减的ε贪婪策略选择动作：
def action(self, state, training = False):
if self.num_training_steps > self.exploration_period:
epsilon = self.final_exploration_epsilon
else:
epsilon = self.initial_exploration_epsilon - float(self.num_training_steps) * (self.initial_exploration_epsilon - self.final_exploration_epsilon) / self.exploration_period
if not training:
epsilon = 0.05
if random.random() <= epsilon:
action = random.randint(0, self.action_size-1)
else:
action = self.session.run(self.predicted_actions, {self.state:[state] } )[0]
return action
现在，我们定义一个train函数来训练我们的网络：
def train(self):
将主要网络权重复制到目标网络：
if self.num_training_steps == 0:
print "Training starts..."
self.qnet.copy_to(self.target_qnet)
记忆回放中的示例经验：
minibatch = self.experience_replay.sample()
从minibatch获取状态，动作，奖励和下一个状态：
batch_states = np.asarray( [d[0] for d in minibatch] )
actions = [d[1] for d in minibatch]
batch_actions = np.zeros( (self.minibatch_size, self.action_size) )
for i in xrange(self.minibatch_size):
batch_actions[i, actions[i]] = 1
batch_rewards = np.asarray( [d[2] for d in minibatch] )
batch_newstates = np.asarray( [d[3] for d in minibatch] )
batch_newstates_mask = np.asarray( [not d[4] for d in minibatch] )
执行训练操作：
scores, _, = self.session.run([self.q_values, self.qnet_optimize],
{ self.state: batch_states,
self.next_state: batch_newstates,
self.next_state_mask: batch_newstates_mask,
self.rewards: batch_rewards,
self.action_mask: batch_actions} )
更新目标网络权重：
if self.num_training_steps % self.target_qnet_update_frequency == 0:
self.session.run( self.hard_copy_to_target )
print 'mean maxQ in minibatch: ',np.mean(np.max(scores,1))
str_ = self.session.run(self.summarize, { self.state: batch_states,
self.next_state: batch_newstates,
self.next_state_mask: batch_newstates_mask,
self.rewards: batch_rewards,
self.action_mask: batch_actions})
self.summary_writer.add_summary(str_, self.num_training_steps)
self.num_training_steps += 1
赛车
到目前为止，我们已经看到了如何构建决斗 DQN。 现在，我们将看到在玩赛车游戏时如何利用我们的决斗 DQN。
首先，让我们导入必要的库：
import gym
import time
import logging
import os
import sys
import tensorflow as tf
初始化所有必需的变量：
ENV_NAME = 'Seaquest-v0'
TOTAL_FRAMES = 20000000
MAX_TRAINING_STEPS = 20 * 60 * 60 / 3
TESTING_GAMES = 30
MAX_TESTING_STEPS = 5 * 60 * 60 / 3
TRAIN_AFTER_FRAMES = 50000
epoch_size = 50000
MAX_NOOP_START = 30
LOG_DIR = 'logs'
outdir = 'results'
logger = tf.train.SummaryWriter(LOG_DIR)
# Intialize tensorflow session
session = tf.InteractiveSession()
构建智能体：
agent = DQN(state_size=env.observation_space.shape,
action_size=env.action_space.n,
session=session,
summary_writer = logger,
exploration_period = 1000000,
minibatch_size = 32,
discount_factor = 0.99,
experience_replay_buffer = 1000000,
target_qnet_update_frequency = 20000,
initial_exploration_epsilon = 1.0,
final_exploration_epsilon = 0.1,
reward_clipping = 1.0,
)
session.run(tf.initialize_all_variables())
logger.add_graph(session.graph)
saver = tf.train.Saver(tf.all_variables())
存储录音：
env.monitor.start(outdir+'/'+ENV_NAME,force = True, video_callable=multiples_video_schedule)
num_frames = 0
num_games = 0
current_game_frames = 0
init_no_ops = np.random.randint(MAX_NOOP_START+1)
last_time = time.time()
last_frame_count = 0.0
state = env.reset()
现在，让我们开始训练：
while num_frames <= TOTAL_FRAMES+1:
if test_mode:
env.render()
num_frames += 1
current_game_frames += 1
给定当前状态，选择操作：
action = agent.action(state, training = True)
在环境上执行操作，接收reward，然后移至next_state：
next_state,reward,done,_ = env.step(action)
将此转移信息存储在experience_replay_buffer中：
if current_game_frames >= init_no_ops:
agent.store(state,action,reward,next_state,done)
state = next_state
训练智能体：
if num_frames>=TRAIN_AFTER_FRAMES:
agent.train()
if done or current_game_frames > MAX_TRAINING_STEPS:
state = env.reset()
current_game_frames = 0
num_games += 1
init_no_ops = np.random.randint(MAX_NOOP_START+1)
在每个周期之后保存网络参数：
if num_frames % epoch_size == 0 and num_frames > TRAIN_AFTER_FRAMES:
saver.save(session, outdir+"/"+ENV_NAME+"/model_"+str(num_frames/1000)+"k.ckpt")
print "epoch: frames=",num_frames," games=",num_games
我们每两个周期测试一次表现：
if num_frames % (2*epoch_size) == 0 and num_frames > TRAIN_AFTER_FRAMES:
total_reward = 0
avg_steps = 0
for i in xrange(TESTING_GAMES):
state = env.reset()
init_no_ops = np.random.randint(MAX_NOOP_START+1)
frm = 0
while frm < MAX_TESTING_STEPS:
frm += 1
env.render()
action = agent.action(state, training = False)
if current_game_frames < init_no_ops:
action = 0
state,reward,done,_ = env.step(action)
total_reward += reward
if done:
break
avg_steps += frm
avg_reward = float(total_reward)/TESTING_GAMES
str_ = session.run( tf.scalar_summary('test reward ('+str(epoch_size/1000)+'k)', avg_reward) )
logger.add_summary(str_, num_frames)
state = env.reset()
env.monitor.close()
我们可以看到智能体如何学习赢得赛车游戏，如以下屏幕截图所示：
总结
在本章中，我们学习了如何详细实现决斗 DQN。 我们从用于游戏画面预处理的基本环境包装器函数开始，然后定义了QNetworkDueling类。 在这里，我们实现了决斗 Q 网络，该网络将 DQN 的最终全连接层分为值流和优势流，然后将这两个流组合以计算q值。 之后，我们看到了如何创建回放缓冲区，该缓冲区用于存储经验并为网络训练提供经验的小批量样本，最后，我们使用 OpenAI 的 Gym 初始化了赛车环境并训练了我们的智能体。 在下一章第 13 章，“最新进展和后续步骤”中，我们将看到 RL 的一些最新进展。
问题
问题列表如下：
- DQN 和决斗 DQN 有什么区别？
- 编写用于回放缓冲区的 Python 代码。
- 什么是目标网络？
- 编写 Python 代码以获取优先级的经验回放缓冲区。
- 创建一个 Python 函数来衰减
ε贪婪策略。 - 决斗 DQN 与双 DQN 有何不同？
- 创建用于将主要网络权重更新为目标网络的 Python 函数。
进一步阅读
以下链接将帮助您扩展知识：
十三、最新进展和后续步骤
恭喜你！ 您已进入最后一章。 我们已经走了很长一段路！ 我们从 RL 的基础知识开始，例如 MDP，蒙特卡洛方法和 TD 学习，然后转向高级深度强化学习算法，例如 DQN，DRQN 和 A3C。 我们还了解了有趣的最新策略梯度方法，例如 DDPG，PPO 和 TRPO，并建立了赛车智能体作为我们的最终项目。 但是 RL 每天还有越来越多的进步供我们探索。 在本章中，我们将学习 RL 的一些进步，然后介绍分层和逆 RL。
在本章中，您将学习以下内容：
- 想象力增强智能体（I2A）
- 从人类偏好学习
- 来自演示的深度 Q 学习
- 事后经验回放
- 分层强化学习
- 逆强化学习
想象力增强智能体
您是国际象棋迷吗？ 如果我要你下棋，你会怎么玩？ 在棋盘上移动任何棋子之前，您可能会想象移动任何棋子并移动您认为会帮助您获胜的棋子的后果。 因此，基本上，在采取任何措施之前，您先想像一下后果，如果有利，则继续进行该措施，否则就不要执行该措施。
同样，想象力增强的智能体也会增加想象力。 在环境中采取任何行动之前，他们会想象采取行动的后果，如果他们认为该行动会带来良好的回报，他们将执行该行动。 他们还想象采取不同行动的后果。 用想象力增强智能体是迈向通用人工智能的下一步。
现在，我们将简短地了解想象力增强智能体的工作原理。 I2A 充分利用了基于模型的学习和基于模型的学习。
I2A 的架构如下：
智能体采取的行动是基于模型的路径和没有模型的路径的结果。 在基于模型的路径中，我们有一些称为“滚动编码器”的产品。 这些推出编码器是智能体执行想象任务的地方。 让我们仔细看一下滚动编码器。 推出编码器如下所示：
推出编码器分为两层：想象未来和编码器。 想象未来是想象力发生的地方。 看上图。 想象未来由想象核心组成。 当将状态o[t]馈送到想象力核心时，我们得到了新状态o_hat[t + 1]和奖励r_hat[t + 1]，当我们将这个新状态o_hat[t + 1]馈给了下一个想象力核心时，我们得到了下一个新状态o_hat[t + 2]和奖励r_hat[t + 2]。 当我们在某些n步骤中重复这些步骤时，我们会得到一个基本上是状态和奖励对的推出，然后我们使用诸如 LSTM 的编码器对该推广进行编码。 结果，我们得到了卷展编码。 这些推出编码实际上是描述未来想象路径的嵌入。 我们将针对未来不同的想象路径使用多个推出编码器，并使用聚合器来聚合此推出编码器。
等待。 想象力如何在想象力核心中发生？ 想象力核心中实际上是什么？ 下图显示了单个想象核心：
想象核心由策略网络和环境模型组成。 环境模型实际上是发生一切的地方。 环境模型从智能体到目前为止执行的所有动作中学习。 它获取有关状态o_hat[t]的信息，并根据经验来想象所有可能的期货，并选择给予较高奖励的操作a_hat[t]。
扩展了所有组件的 I2A 架构如下所示：
您以前玩过推箱子吗？ 推箱子是一款经典的益智游戏，玩家必须将盒子推到目标位置。 游戏的规则非常简单：盒子只能推入而不能拉出。 如果我们向错误的方向推箱子，那么难题将变得无法解决：
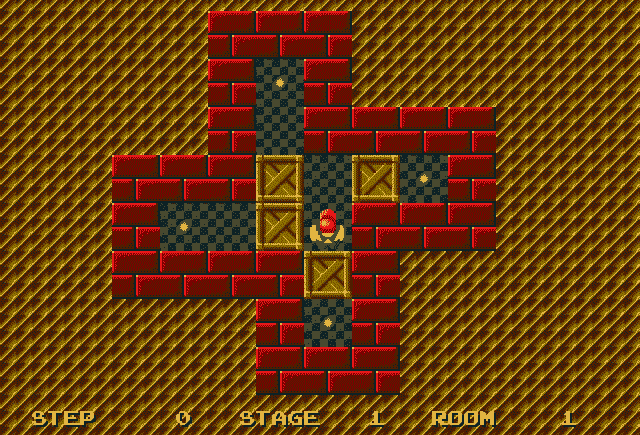
如果我们被要求玩推箱子，那么在做出任何举动之前，我们会想一想并计划好，因为糟糕的举动会导致游戏结束。 I2A 架构将在此类环境中提供良好的结果，在这种环境中，智能体必须提前计划才能采取任何措施。 本文的作者在推箱子上测试了 I2A 表现，并取得了显著成果。
从人类偏好学习
向人类学习是 RL 的重大突破。 该算法由 OpenAI 和 DeepMind 的研究人员提出。 该算法背后的思想是使智能体根据人的反馈进行学习。 最初，智能体会随机行动，然后将执行动作的智能体的两个视频片段提供给人类。 人们可以检查视频剪辑，并告诉智能体哪个视频剪辑更好，也就是说，智能体在哪个视频中更好地执行任务，并将其实现目标。 给出反馈后，智能体将尝试执行人类喜欢的操作并相应地设置奖励。 设计奖励函数是 RL 中的主要挑战之一，因此，与智能体进行人为互动可以直接帮助我们克服挑战，也可以最大程度地减少编写复杂目标函数的过程。
训练过程如下图所示：
让我们看一下以下步骤：
- 首先，我们的智能体通过随机策略与环境交互。
- 智能体与环境交互的行为将在两到三秒钟的视频剪辑对中捕获并提供给人类。
- 人员将检查视频剪辑，并了解智能体在哪个视频剪辑中表现更好。 他们会将结果发送给奖励预测器。
- 现在，智能体将从预测的奖励中接收这些信号，并根据人类的反馈设置其目标和奖励函数。
轨迹是一系列观察和动作。 我们可以将轨迹段表示为σ，因此σ = (o0, a0), (o1, a1), ..., (o[k-1], a[k-1])，其中o是观察值，a是动作。 智能体从环境接收观察并执行某些操作。 假设我们将交互序列存储在两个轨迹段中，即σ[1]和σ[2]。 现在，这两个轨迹已显示给人类。 如果人类更喜欢σ[2]而不是σ[1]，那么智能体的目标是产生人类所喜欢的轨迹，并相应地设置奖励函数。 这些轨迹段以(σ[1], σ[2], μ)的形式存储在数据库中； 如果人类更喜欢σ[2]而不是σ[1]，则μ设置为更喜欢σ[2]。 如果没有一条轨迹是可取的，则两条轨迹都将从数据库中删除。 如果两者均首选，则将μ设置为统一。
您可以在这个页面上查看视频，以了解算法的工作原理。
来自演示的深度 Q 学习
我们已经了解了很多有关 DQN 的知识。 我们从原始 DQN 开始，然后看到了各种改进，例如双重 DQN，决斗的网络架构和优先级的经验回放。 我们还学会了构建 DQN 来玩 Atari 游戏。 我们将智能体与环境的交互存储在经验缓冲区中，并使智能体从这些经验中学习。 但是问题是，我们花了很多训练时间来提高表现。 对于在模拟环境中学习，这很好，但是当我们让智能体在现实环境中学习时，会引起很多问题。 为了克服这个问题，谷歌公司 DeepMind 的研究人员在演示（DQfd）的基础上，对 DQN 进行了改进，称为深度 Q 学习。
如果我们已经有了一些演示数据，则可以将这些演示直接添加到经验回放缓冲区中。 例如，考虑一个学习玩 Atari 游戏的智能体。 如果我们已经有了一些演示数据来告诉我们的智能体，哪个状态更好，哪个动作可以提供良好的回报，那么智能体可以直接使用此数据进行学习。 即使是少量的演示，也可以提高智能体的表现并最大程度地减少训练时间。 由于演示的数据将直接添加到优先经验回放缓冲区中，因此智能体可以从演示数据中使用的数据量以及智能体可以从其自己的交互中用于学习的数据量将由优先经验回放来控制缓冲区，因为经验将被优先考虑。
DQfd 中的损失函数将是各种损失的总和。 为了防止我们的智能体过度适合演示数据，我们在网络权重上计算 L2 正则化损失。 我们像往常一样计算 TD 损失，也计算监督损失，以了解我们的智能体如何从演示数据中学习。 本文的作者在 DQfd 和各种环境下进行了实验，并且 DQfd 的表现比双重决斗 DQN 优先排序的表现更好，更快。
您可以观看此视频，以了解 DQfd 如何学会玩“Private Eye”游戏。
事后经验回放
我们已经了解了如何在 DQN 中使用经验回放来避免相关经验。 此外，我们了解到，优先经验回放是对原始经验回放的一种改进，因为它优先考虑 TD 误差的每个经验。 现在，我们将研究由 OpenAI 研究人员提出的一种用于处理稀疏奖励的名为事后经验回放（HER）的新技术。 您还记得如何学习骑自行车吗？ 第一次尝试时，您将无法正确平衡自行车。 您可能多次无法正确平衡。 但是，所有这些失败并不意味着您没有学到任何东西。 失败会教你如何不平衡自行车。 即使您没有学会骑自行车（目标），您也学习了一个不同的目标，即，您学会了如何不平衡自行车。 这是我们人类学习的方式，对吗？ 我们从失败中学习，这就是事后回顾经验的想法。
让我们考虑本文中给出的相同示例。 如图所示，查看 FetchSlide 环境。 在这种环境下的目标是移动机械臂并在桌子上滑动冰球以击中目标，这是一个红色的小圆圈（图表来自这里）：
在最初的几次尝试中，智能体不一定能实现目标。 因此，智能体只收到 -1 作为奖励，这告诉智能体他做错了，没有达到目标：
但这并不意味着智能体没有学到任何东西。 智能体已经实现了一个不同的目标，即它学会了接近实际目标。 因此，我们认为它有一个不同的目标，而不是认为它是失败的。 如果我们在多次迭代中重复此过程，智能体将学会实现我们的实际目标。 HER 可以应用于任何非策略算法。 将 HER 的表现与没有 HER 的 DDPG 进行比较，反之亦然，可以看出带有 HER 的 DDPG 的收敛速度比没有 HER 的 DDPG 快。 您可以在以下视频中看到 HER 的表现。
分层强化学习
RL 的问题在于它无法在大量状态空间和动作下很好地扩展，最终导致维度的诅咒。 分层强化学习（HRL）被提出来解决维数的诅咒，其中我们将大问题解压缩为层次结构中的小子问题。 假设智能体的目标是从学校到达家中。 在这里，问题被分解为一组子目标，例如从学校大门出来，预定出租车等。
HRL 中使用了不同的方法，例如状态空间分解，状态抽象和时间抽象。 在状态空间分解中，我们将状态空间分解为不同的子空间，并尝试在较小的子空间中解决问题。 分解状态空间还可以加快探查速度，因为智能体程序不希望探究整个状态空间。 在状态抽象中，智能体会忽略与在当前状态空间中实现当前子任务无关的变量。 在时间抽象中，将动作序列和动作集分组，这将单个步骤分为多个步骤。
现在，我们可以研究 HRL 中最常用的算法之一，称为 MAXQ 值函数分解。
MAXQ 值函数分解
MAXQ 值函数分解是 HRL 中最常用的算法之一。 让我们看看 MAXQ 的工作原理。 在 MAXQ 值函数分解中，我们将值函数分解为每个子任务的一组值函数。 让我们以本文中给出的相同示例为例。 还记得我们使用 Q 学习和 SARSA 解决的出租车问题吗？
总共有四个地点，智能体必须在一个地点接客并在另一地点下车。 智能体将获得 +20 积分作为成功下车的奖励，而每走一步便获得 -1 积分。 该智能体还将因非法取送丢掉 -10 分。 因此，我们智能体的目标是学会在短时间内在正确的位置上落客而不增加非法乘客。
接下来显示的是环境，其中的字母（R，G，Y，B）代表不同的位置， 黄色矩形是由我们的智能体驾驶的出租车：
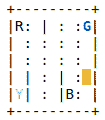
现在，我们将目标分为以下四个子任务：
- 导航：这里的目标是将出租车从当前位置驾驶到目标位置之一。 导航子任务应使用北，南，东和西四个原始动作。
- 获取：这里的目标是将出租车从当前位置驾驶到乘客的位置并接客。
- 放置：这里的目标是将出租车从当前位置驾驶到乘客的目的地位置并下车。
- 根：根是整个任务。
我们可以在称为任务图的有向无环图中表示所有这些子任务，如下所示：
您可以在上图中看到所有子任务都是按层次排列的。 每个节点代表子任务或原始动作，并且每个边都连接一个子任务可以调用其子子任务的方式。
导航子任务具有四个原始动作：东部，西部，北部和南部。获取子任务具有拾取基本操作和导航子任务； 同样，放置子任务，具有放置（放置）原始动作并导航子任务。
在 MAXQ 分解中，MDP 
将分为一组任务，例如(M[0], M[1], ,,, M[n])。
M[0]是根任务，M[1], M[2], M[n]是子任务。
子任务M[i]使用状态S[i]，操作A[i]，概率转换函数P[i]^π(s', N | s, a)和预期奖励函数R_bar(s, a) = V^π(a, s)定义半 MDP，其中V^π(a, s)是子任务M[a]在s状态下的投影值函数。
如果动作a是原始动作，那么我们可以将V^π(a, s)定义为在s状态下执行动作a的预期立即回报：
现在，我们可以按贝尔曼方程形式重写前面的值函数，如下所示：
----（1）
我们将状态动作值函数Q表示如下：
----（2）
现在，我们再定义一个称为完成函数的函数，它是完成子任务M[i]的预期折扣累积奖励：
----（3）
对于方程式(2)和(3)，我们可以将 Q 函数写为：
最后，我们可以将值函数重新定义为：
前面的等式会将根任务的值函数分解为各个子任务任务的值函数。
为了高效地设计和调试 MAXQ 分解，我们可以按如下方式重绘任务图：
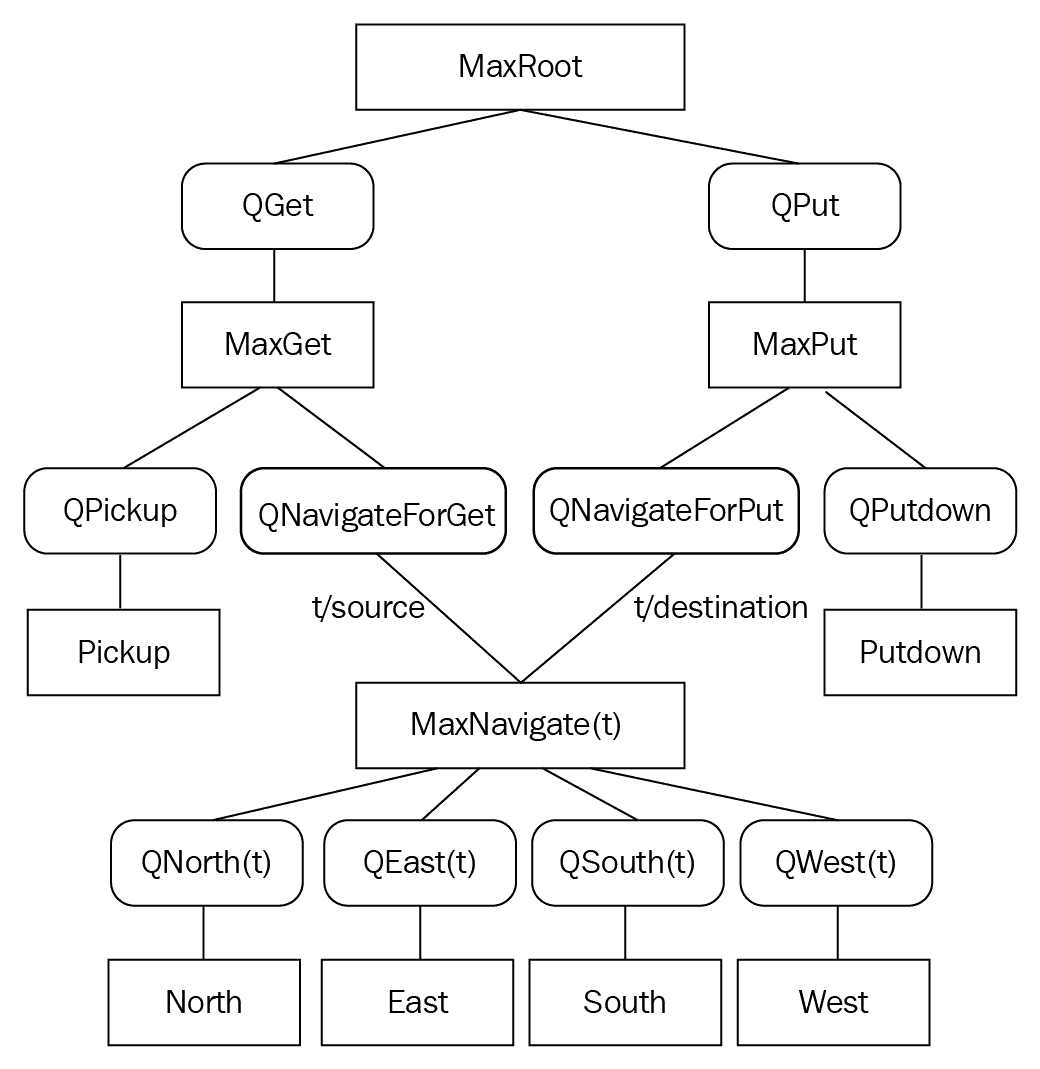
我们重新设计的图包含两种特殊类型的节点：最大节点和 Q 节点。 最大节点定义任务分解中的子任务，而 Q 节点定义可用于每个子任务的动作。
逆强化学习
那么，我们在 RL 中做了什么？ 我们试图找到具有奖励函数的最优策略。 逆强化学习只是强化学习的逆，也就是说，给出了最优策略，我们需要找到奖励函数。 但是为什么反强化学习会有所帮助？ 设计奖励函数不是一项简单的任务，而较差的奖励函数会导致智能体的不良行为。 我们并不总是知道适当的奖励函数，但我们知道正确的策略，即在每个状态采取正确的行动。 因此，这种最佳策略由人类专家提供给智能体，智能体尝试学习奖励函数。 例如，考虑一个学习在真实环境中行走的智能体； 很难为将要执行的所有动作设计奖励函数。 取而代之的是，我们可以将人类专家的演示（最佳策略）提供给智能体，智能体将尝试学习奖励函数。
RL 周围有各种改进和进步。 现在，您已经阅读完本书，可以开始探索强化学习的各种进步，并开始尝试各种项目。 学习和加强！
总结
在本章中，我们了解了 RL 的一些最新进展。 我们看到了 I2A 架构如何将想象力核心用于前瞻性计划，然后如何根据人的喜好来训练智能体。 我们还了解了 DQfd，它可以通过从演示中学习来提高 DQN 的表现并减少其训练时间。 然后，我们研究了事后的经验回放，从中我们了解了智能体如何从失败中学习。
接下来，我们学习了层次 RL，其中目标被解压缩为子目标层次。 我们了解了反向 RL，其中智能体尝试根据给定策略来学习奖励函数。 RL 每天都在以有趣的进步发展。 既然您已经了解了各种强化学习算法，则可以构建智能体以执行各种任务并为 RL 研究做出贡献。
问题
问题列表如下：
- 智能体的想象力是什么？
- 想象力的核心是什么？
- 智能体如何从人的偏好中学习？
- DQfd 与 DQN 有何不同？
- 什么是事后经验回放？
- 分层强化学习有什么需求？
- 逆强化学习与强化学习有何不同？
进一步阅读
您可以进一步参考以下论文：
十四、答案
第 1 章
- 强化学习（RL）是机器学习的一个分支，其中学习是通过与环境交互来进行的。
- 与其他 ML 范例不同，RL 通过训练和误差方法工作。
- 智能体是做出明智决策的软件程序，它们基本上是 RL 的学习器。
- 策略函数指定在每个状态下要执行的操作，而值函数指定每个状态的值。
- 在基于模型的智能体中，使用以前的经验，而在无模型的学习中，则不会有任何以前的经验。
- 确定性的，随机的，完全可观察的，部分可观察的，离散的连续的，事件的和非事件的。
- OpenAI Universe 为训练 RL 智能体提供了丰富的环境。
- 请参阅 RL 的“应用”部分。
第 2 章
-
conda create --name universe python=3.6 anaconda -
使用 Docker，我们可以将应用及其依赖关系打包，称为容器，并且我们可以在服务器上运行应用，而无需将任何外部依赖关系与打包的 Docker 容器一起使用。
-
gym.make(env_name) -
from gym import envs
print(envs.registry.all()) -
OpenAI Universe 是 OpenAI Gym 的扩展，还提供各种丰富的环境。
-
占位符用于提供外部数据，而变量用于保持值。
-
TensorFlow 中的所有内容都将表示为由节点和边组成的计算图，其中节点是数学运算（例如加法，乘法等），而边是张量。
-
计算图只会被定义； 为了执行计算图，我们使用 TensorFlow 会话。
第 3 章
- 马尔可夫性质指出，未来仅取决于现在而不是过去。
- MDP 是马尔可夫链的延伸。 它提供了用于建模决策情况的数学框架。 几乎所有的 RL 问题都可以建模为 MDP。
- 请参阅“折扣系数”部分。
- 折扣系数决定了我们对未来奖励和即时奖励的重视程度。
- 我们使用贝尔曼函数求解 MDP。
- 有关值和 Q 函数的信息，请参见“推导贝尔曼方程”部分。
- 值函数指定状态的优劣，而 Q 函数指定状态下的行为的优劣。
- 请参阅“值迭代”和“策略迭代”部分。
第 4 章
-
当环境模型未知时，在 RL 中使用蒙特卡洛算法。
-
请参阅“使用蒙特卡洛估计
pi的值”部分。 -
在蒙特卡洛预测中，我们通过取均值回报而不是期望回报来近似值函数。
-
在蒙特卡洛的每次访问中，我们平均将剧集中每次访问状态的收益均值化。 但是在首次访问 MC 方法中，我们仅在剧集中首次访问状态时才对返回值进行平均。
-
请参阅“蒙特卡洛控制”部分。
-
请参阅“策略上的蒙特卡洛控制”和“策略外的蒙特卡洛控制”部分
-
请参阅“让我们使用蒙特卡洛玩二十一点”部分。
第 5 章
- 蒙特卡罗方法仅适用于剧集任务，而 TD 学习可应用于剧集任务和非剧集任务
- 实际值与预测值之差称为 TD 误差
- 请参阅“TD 预测”和“TD 控制”部分
- 请参阅“使用 Q 学习解决滑行问题”部分
- 在 Q 学习中，我们使用
ε贪婪策略采取行动，并且在更新 Q 值的同时，我们仅采取最大行动。 在 SARSA 中，我们使用ε贪婪策略采取措施，并且在更新 Q 值的同时，我们使用ε贪婪策略采取措施。
第 6 章
- MAB 实际上是一台老丨虎丨机，是一种在赌场玩的赌博游戏，您可以拉动手臂（杠杆）并根据随机生成的概率分布获得支出（奖励）。 一台老丨虎丨机称为单臂老丨虎丨机，当有多台老丨虎丨机时，称为多臂老丨虎丨机或 k 臂老丨虎丨机。
- 当业务代表不确定是使用以前的经验来探索新动作还是利用最佳动作时，就会出现探索-利用困境。
- ε用于确定智能体是否应使用
1-ε进行探索或利用我们选择最佳作用的作用，而使用ε则探索新作用。 - 我们可以使用各种算法（例如
ε贪婪策略，softmax 探索，UCB，Thompson 采样）解决探索-利用难题。 - UCB 算法可帮助我们根据置信区间选择最佳分支。
- 在 Thomson 抽样中，我们使用先验分布进行估计，而在 UCB 中，我们使用置信区间进行估计。
第 7 章
- 在神经元中，我们通过应用称为激活或传递函数的函数
f()将非线性引入结果z。 请参阅“人工神经元”部分。 - 激活函数用于引入非线性。
- 我们计算成本函数相对于权重的梯度以最小化误差。
- RNN 不仅基于当前输入，而且还基于先前的隐藏状态来预测输出。
- 在网络反向传播时，如果梯度值变得越来越小，则称为消失梯度问题，如果梯度值变得更大，则它正在爆炸梯度问题。
- 门是 LSTM 中的特殊结构，用于决定保留，丢弃和更新哪些信息。
- 池化层用于减少特征映射的维数，并且仅保留必要的细节，因此可以减少计算量。
第 8 章
- 深度 Q 网络（DQN）是用于近似 Q 函数的神经网络。
- 经验回放用于删除智能体经验之间的相关性。
- 当我们使用同一网络来预测目标值和预测值时，会有很多差异，因此我们使用单独的目标网络。
- 由于最大运算符，DQN 高估了 Q 值。
- 通过具有两个单独的 Q 函数，每个学习都独立地加倍 DQN，从而避免了高估 Q 值的情况。
- 经验是优先经验回放中基于 TD 误差的优先级。
- DQN 通过将 Q 函数计算分解为值函数和优势函数来精确估计 Q 值。
第 9 章
- DRQN 利用循环神经网络（RNN），其中 DQN 利用原始神经网络。
- 当可以部分观察 MDP 时，不使用 DQN。
- 请参阅“DRQN 的 Doom”部分。
- 与 DRQN 不同，DARQN 利用注意力机制。
- DARQN 用于理解和专注于游戏屏幕的特定区域，这一点更为重要。
- 软硬注意力。
- 即使该举动无用，我们也将智能体的每次举动设置为活奖赏 0。
第 10 章
- A3C 是“异步优势演员评论家网络”，它使用多个智能体进行并行学习。
- 三个 A 是异步，优势，演员评论家。
- 与 DQN 相比，A3C 需要更少的计算能力和训练时间。
- 所有智能体（员工）都在环境副本中工作，然后全局网络汇总他们的经验。
- 熵用于确保足够的探索。
- 请参阅“A3C 的工作方式”部分。
第十一章
-
策略梯度是 RL 中令人惊奇的算法之一，在该算法中，我们直接优化由某些参数设置参数的策略。
-
策略梯度是有效的，因为我们无需计算 Q 函数即可找到最佳策略。
-
演员网络的作用是通过调整参数来确定状态中的最佳动作，而评论家的作用是评估演员产生的动作。
-
请参阅“信任区域策略优化”部分
-
我们迭代地改进了该策略，并施加了一个约束，即旧策略和新策略之间的 Kullback-Leibler（KL）差异要小于某个常数。 该约束称为信任区域约束。
-
PPO 通过将约束更改为惩罚项来修改 TRPO 的目标函数，因此我们不想执行共轭梯度。
第十二章
- DQN 直接计算 Q 值，而决斗 DQN 将 Q 值计算分解为值函数和优势函数。
- 请参阅“记忆回放”部分。
- 当我们使用同一网络来预测目标值和预测值时，会有很多差异，因此我们使用单独的目标网络。
- 请参阅“记忆回放”部分。
- 请参阅“决斗网络”部分。
- 决斗 DQN 将 Q 值计算分解为值函数和优势函数，而双 DQN 使用两个 Q 函数来避免高估。
- 请参阅“决斗网络”部分。
第十三章
-
智能体中的想象力指定了采取任何行动之前的可视化和计划。
-
想象力核心由执行想象力的策略网络和环境模型组成。
-
智能体反复从人类那里获得反馈，并根据人类的喜好改变目标。
-
DQfd 使用一些演示数据进行训练，因为 DQN 并未预先使用任何演示数据。
-
请参阅事后经验回放（HER）部分。
-
提出了分层强化学习（HRL），以解决维数诅咒，其中我们将大问题解压缩为层次结构中的小子问题
-
我们试图在 RL 中找到给定奖励函数的最优策略，而在逆向强化学习中，给出最优策略并找到奖励函数