主定理:
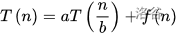
n为问题规模,a为递推的子问题数量,n/b为每个子问题的规模,f(n)为递推意以外进行的计算工作。
a≥1,b>1为常数,f(n) 为函数,T(n) 为非负整数。则有以下结果(分类讨论):
1)若 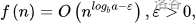 则有
则有
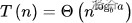
2)若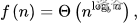 则有
则有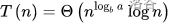
3)若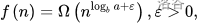 且对于某个常数c<1和所有充分大的n有
且对于某个常数c<1和所有充分大的n有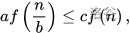
则有
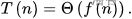
其中,大O代表的是该算法的算法复杂度上限,即该算法在最坏情况之下的复杂度。f(x) = O(g(x))正式的数学定义:存在正常数c,n,n0,当n>n0时,对于任意f(n)符合0<=f(n)<=c*g(n) ,如图:
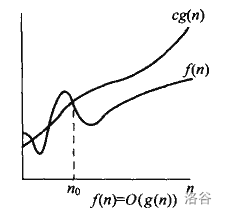
从这张图可以看出,当横坐标的值大于x=n0时,cg(n)的纵值总大于f(n),这可以理解为f(x)以g(n)为上界。
大omega则是代表该算法的算法复杂度下限,即该算法在最优情况之下的复杂度。 f(n)= Ω(g(n)) 正式的数学定义:存在正常数c、n、n0,当 n > n0 的时,任意的 f(n) 符合 0 <= c*g(n) <= f(n)。如图:
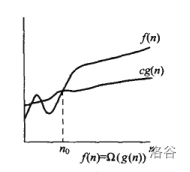
同理,我们可以从图中看出,在n0之后cg(n)总比f(n)小,因此可以理解为f(x)以g(n)为下界。
大theta是算法复杂度的确界,他既描述了上界,又描述了下界。
f(n)= θ(cg(n)) 正式的数学定义:存在正常数c1、c2、n、n0,当 n > n0 的时,对于任意的f(n)对符合 c1g(n) <= f(n) <= c2g(n),c1g(n)、c2*g(n)都是渐进正函数(当n趋于无穷大的时候,f(n)为正)。 如图:
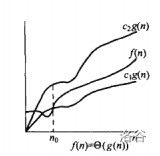
算法导论中还根据大O,大Ω,大θ的定义得到以下定理:
当且仅当函数 f(n) = O(g(n)) 并且 f(n)= Ω(g(n)) 时,才有 f(n) = θ(g(n))。
回到主定理,可以看出,只要求出log以b为底的a的n次方,复杂度就可以很快的算出来,我们把公式用刚介绍的概念翻译一下:
1)若f(n)以log以b为底的a-ε的n次方为上界,则该递推式的算法复杂度的确界为log以b为底的a的n次方
2)若f(n)以log以b为底的a的n次方为确界,则该递推式的算法复杂度的确界为log以b为底的a的n次方乘以logn
3)若f(n)以log以b为底的a+ε的n次方为下界,且n充分大,则该递推式的算法复杂度的确界为f(n)
标签:log,定理,次方,算法,n0,为底,复杂度 From: https://www.cnblogs.com/reasa/p/16847908.html