提示:代码还没写(但感觉不难写)。
抄一下 https://www.luogu.com.cn/article/n32presk,写的非常好。
下面是要把问题转化为一个群论问题。
定义拓扑空间:全集 \(X\) 和它的一个子集族 \(T\),使得 \(\varnothing,X\in T\),且任意有限个元素的交在 \(T\) 中,任意元素(不要求有限或可数)的并在 \(T\) 中。
则称 \((X,T)\) 是拓扑空间,\(T\) 内元素叫开集,不在的是闭集。
拓扑空间之间的函数 \(f:X\to Y\) 是连续的,当且仅当 \(\forall t\in T_Y\),\(f^{-1}(t)\in T_X\)(数学分析中有形式一样的度量空间上的结论)
对于这道题,不用太在意这个定义,因为 \(\R,\R^2\) 及其子空间的开集概念是熟知的。
下记 \(S^1\) 为单位圆(就是首尾相接的 \([0,1]\))。
对于拓扑空间 \(X\),一条道路是 \(f:[0,1]\to X\) 的函数,一条闭曲线/回路是 \(f:S^1\to X\) 的连续函数。
下面一段直接在道路 \(C,D:X\to Y\) 的意义下说了。
闭曲线 \(C\) 到 \(D\) 存在连续变化,当且仅当存在连续函数 \(F:X\times [0,1]\to Y\),使得 \(F(x,0)=C(x),F(x,1)=D(x)\),此时称 \(C,D\) 同伦。若还满足 \(F(0,x)=C(0)=D(0),F(1,x)=C(1)=D(1)\),这称为定端同伦,记为 \([C]=[D]\)。
定端同伦关系构成等价类,即 \([C]\) 代表和 \(C\) 定端同伦的等价类。
定义道路 \(C(0)=x,C(1)=D(0)=y,D(1)=z\) 的乘积 \(C*D\):把 \(C\) 放在 \([0,0.5]\),\(D\) 放在 \([0.5,1]\),显然还是连续;扩展到等价类上,等价类的 \(*\) 是满足
\[[C]*[D]=[C*D] \]的运算。
对于定点 \(z\) 到自己的回路,这样的等价类和 \(*\) 构成群,其中单位元 \(e\mapsto e(x)=z\),而把回路翻转构成了逆元。这称为基本群 \(\pi(X,z)\)。
一个拓扑空间 \(X\) 有强形变收缩核 \(A\subset X\),当 \(e(x)=x\) 和一个连续函数 \(r:X\to A\) 同伦,且同伦函数 \(H\) 满足 \(\forall a\in A,t,H(a,t)=a\)(即 \(A\) 内部不变)。这个同伦把 \([f]\in \pi(X,z)\) 同到了 \([r\circ f]\in \pi(A,z)\)。
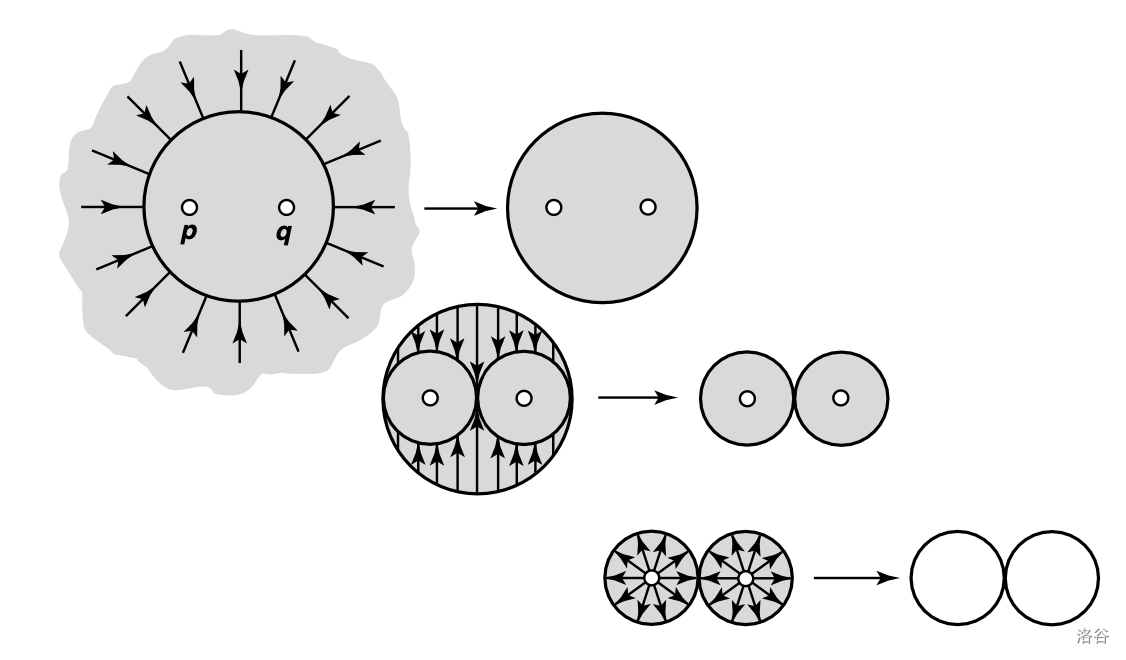
这表明 \(\R^2-\{x\}-\{y\}\) 可以收缩到两个 \(S^1\) 在一个点上拼起来,记为 \(S^1\lor S^1\)。显然,\(\R^2-\{x_1,x_2\dots x_n\}\) 可以收缩到 \(S^1\lor S^1\lor\dots \lor S^1\),只需考虑 \(\pi(S^1\lor S^1\lor\dots \lor S^1,z)\) 的结构。
不难看出(?) \(\pi (S^1,z)=\Z\)。而有:
塞弗特-范坎彭定理:\(\pi(A\cup B,z)=\pi(A,z)*\pi(A\cap B,z)*\pi(B,z)\),其中 \(*\) 是群自由积。
所以,\(\pi(S^1\lor S^1\lor\dots \lor S^1,z)=\Z*\Z*\dots *\Z\)。对于本题的条件,记点集为 \(S=\{x_1,x_2,\dots x_n\}\);这可以被看作是 \(x_i\) 及 \(x_i^{-1}\) 构成的串集合。
对于 \(T\subset S\),考虑嵌入 \(\iota :\R^2-S\to \R^2-T\) 及其给出的同态 \(\varphi_{S\to T}:\pi(\R^2-S,z)\to \pi(\R^2-T,z)\),这个同态具体是对于 \(i\not\in T\),\(x_i\) 成为单位元 \(e\),否则不变,而这些 \(i\to T\) 的自由群就是 \(\R^2-T\)。
一个闭曲线是同伦于单位元 \(e\) 的。那么问题变为:
对于一个自由群 \(F(x_1,x_2\dots x_n)\),找出 \(w\in F\),使得 \(\forall T\subset S,[\varphi_{S\to T}(w)=e]=A_T\)。
首先必须满足 \(A_0=1\),并且 \(\forall R\subset T,A_R\ge A_T\)。下面构造展示,这也是充要条件。
记两元素的交换子是 \([x,y]=xyx^{-1}y^{-1}\)。由于同态性,\(\varphi([x,y])=[\varphi(x),\varphi(y)]\)。这有的好性质是 \([e,x]=[x,e]=e\)。
记 \(w_x=x\),\(w_{S}=w_{\{x_1,x_2\dots x_m\}}=[w_x,w_{S-\{x_1\}}]\)。如果限制为 \(A_T=[S\neq T]\),则可构造 \(w_S\) 满足条件(可以归纳验证)。
进一步地,取出极小的 \(A_{R_i}=0\)。则可以验证,
\[\prod_i w_{R_i} \]满足条件。总路径长度是 \(O(n3^n)\) 的。
标签:dots,同伦,拓扑,AGC043E,varphi,lor,pi From: https://www.cnblogs.com/british-union/p/18667225/topo_hede