前言:
模拟赛考到了此类题目,出现过很多次了,就去小小学习了一下,发现其实挺简单的。
前置知识:
-
线段树(这个知识点如果没有掌握先自行学习,学完再来看,因为本人太弱了,没有写这个的讲解)
-
动态开点线段树(这个知识点如果没有掌握先自行学习,学完再来看)
引入:
在一些树形结构中子节点的贡献要上传到父亲节点时,一些关于子树信息需要用到线段树维护的上传时就需要合并当前所有子节点的线段树信息,但是线段树是一颗满二叉树,如果直接去合并的话时间复杂度肯定不优,所以线段树合并就应运而生了。
正文:
首先我们知道如果两棵树中扫同一个位置的节点时如果有一棵线段树没有当前节点的话,那么新树的当前节点直接是有值的即可。而如果两个都有的话就继续往下搜,直到搜索到没有值的或者是叶子结点。(和合并两棵平衡树很相似,但是这里左右儿子都需要去合并,而不像平衡树可以只合一半)
对于时间复杂度的分析,因为我们知道只有两棵线段树的公共部分我们才会去合并,其他的情况都不需要(如下图中我们就只需要往下扫左右儿子合并的位置是1,2,3,其他的直接合并即可)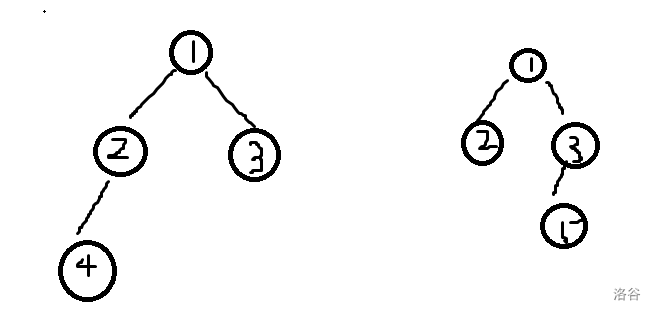
那么时间复杂度其实就是两棵子树的公共部分,而如果题目中的询问次数不是很多的话其实时间复杂度并不高,综合时间复杂度大概是 O(N logV) ,\(V\) 是值域大小,可以放心大胆的使用。
对于写法方面就更简单了,我们就按照这个方式合并,同时更改当前节点的左右儿子即可,然后和普通线段树一样正常上传(板题讲解里面会出现代码)。
板题讲解:
讲解:
[Vani有约会] 雨天的尾巴 /【模板】线段树合并 - 洛谷
这道题首先我们会发现我们可以给每一个点开一颗线段树,记录不同的救济粮有多少。那么答案显然就是这颗线段树中数值最大的点的下标。但是如果直接这样去写,不仅空间复杂度会爆炸,时间复杂度也会爆炸。这样的情况下我们考虑树上差分(和普通差分差不多,就是放到了树上)。在当前需要加的两个端点线段树上加贡献,发现如果一直贡献上传父亲到二者的 \(lca\) 除就不用了,所以我们只用在 \(lca\) 以及他的父亲上删除贡献就可以了。
这样记录之后直接一遍深搜,把儿子节点的贡献上传父亲,用线段树合并即可。
代码:
#include<bits/stdc++.h>
#define int long long
#define ls tr[p].ch[0]
#define rs tr[p].ch[1]
#define mid (l+r)/2
using namespace std;
vector<int>s[100005];int cnt;int top;
//树链剖分维护lca(这里可以换成倍增之类的)
struct f{int dfn,fa,top,siz,son,dep;}t[100005];
void dfs(int p,int fa){t[p].fa=fa,t[p].siz=1,t[p].dep=t[fa].dep+1;for(int i=0;i<s[p].size();i++){int y=s[p][i];if(y==fa) continue;dfs(y,p);t[p].siz+=t[y].siz;if(t[y].siz>t[t[p].son].siz) t[p].son=y;}}
void dfs1(int p,int top){t[p].top=top;t[p].dfn=++cnt;if(t[p].son) dfs1(t[p].son,top);for(int i=0;i<s[p].size();i++){int y=s[p][i];if(y==t[p].fa||y==t[p].son) continue;dfs1(y,y);}}
int lca(int x,int y){while(t[x].top!=t[y].top){if(t[t[x].top].dep<t[t[y].top].dep) swap(x,y);x=t[t[x].top].fa;}return (t[x].dep<t[y].dep?x:y);}
//
struct ff{int sum,ch[2],ma;}tr[100005*16*4];
void wei(int p){if(tr[ls].sum>=tr[rs].sum) tr[p].ma=tr[ls].ma,tr[p].sum=tr[ls].sum;else tr[p].ma=tr[rs].ma,tr[p].sum=tr[rs].sum;}
void xiugai(int &p,int l,int r,int d,int k){
if(!p){p=++top;}//动态开点,没有当前节点就开上
if(l==r){tr[p].sum+=k,tr[p].ma=l;return;}
if(d<=mid) xiugai(ls,l,mid,d,k);
else xiugai(rs,mid+1,r,d,k);wei(p);
}
void merge(int &x,int y,int l,int r){
if(!x||!y){x+=y;return;}
if(l==r){tr[x].sum+=tr[y].sum,tr[x].ma=l;return;}
merge(tr[x].ch[0],tr[y].ch[0],l,mid),merge(tr[x].ch[1],tr[y].ch[1],mid+1,r);
wei(x);
}
int root[100005],ans[100005];
void dpp(int p,int fa){//深搜一遍,做子树上的线段树合并
for(int i=0;i<s[p].size();i++){
int y=s[p][i];if(y==fa) continue;
dpp(y,p);merge(root[p],root[y],1,100000);
}
if(tr[root[p]].sum==0) ans[p]=0;
else ans[p]=tr[root[p]].ma;
}
signed main(){
int n,m;cin>>n>>m;
for(int i=1;i<n;i++){int x,y;cin>>x>>y;s[x].push_back(y),s[y].push_back(x);}
dfs(1,0);dfs1(1,1);
while(m--){
int x,y,z;cin>>x>>y>>z;
xiugai(root[x],1,100000,z,1);//做树上差分,因为要一直上传,所以只用在lca及其父亲上减去贡献即可
xiugai(root[y],1,100000,z,1);
int lc=lca(x,y);
xiugai(root[lc],1,100000,z,-1);
if(t[lc].fa) xiugai(root[t[lc].fa],1,100000,z,-1);
}
dpp(1,0);
for(int i=1;i<=n;i++) cout<<ans[i]<<'\n';
return 0;
}