前言
模拟赛 solution 里说
只需要利用线段树合并的思想……
但是我不会线段树合并,就先学习了线段树合并。
引入
线段树合并是把每个对应节点合并。
两棵线段树都有某个节点,就是把这两个点合成一个点;
只有一棵线段树有某个节点,合并出来的线段树的这个节点就是这个唯一的节点。
两棵线段树都没有这个节点,合并完之后还是没有。
可以看得出来,如果是一般的线段树(是满二叉树)合并就是暴力,所以线段树合并一般是在动态开点线段树之间进行的。
动态开点线段树
当值域很大,操作数不多时,线段树有很多浪费的空间,这时候就需要动态开点线段树。
在这棵线段树上修改节点 \(3\) 的值时,只需要用到三个节点(标红的节点)。
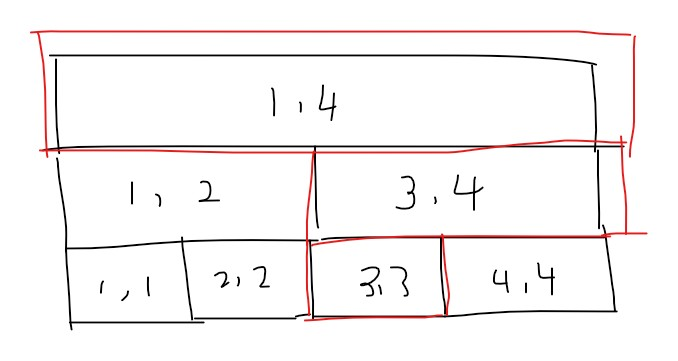
每一个节点记录下左儿子和右儿子,当需要某个节点却没有时,新建一个节点。
代码如下:
void ins(int &p,int l,int r,int x,int v){
if(!p) p=++cnt;
if(l==r){
sum[p]+=v;
return;
}
int mid=(l+r)>>1;
if(x<=mid) ins(lc[p],l,mid,x,v);
else ins(rc[p],mid+1,r,x,v);
push_up(p);
}
查询的时候,需要注意不存在的节点不能计入答案。代码如下:
int ask(int p,int l,int r,int ql,int qr){
if(!p) return 0;
if(ql<=l&&r<=qr) return sum[p];
int mid=(l+r)>>1,res=0;
if(ql<=mid) res+=ask(lc[p],l,mid,ql,qr);
if(qr>mid) res+=ask(rc[p],mid+1,r,ql,qr);
return res;
}
线段树合并
主要有两种写法。
-
把 \(b\) 合并到 \(a\) 上。
这种写法会丢失合并前树的信息,所以只能离线下来。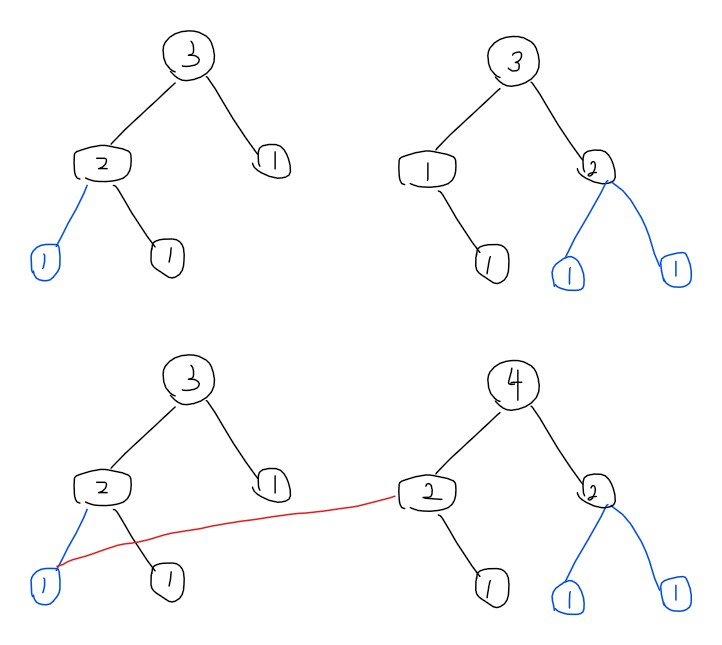
代码还是很好理解的:
int merge(int a,int b,int l,int r){ if(!a||!b) return a|b; if(l==r){ sum[a]+=sum[b]; return a; } int mid=(l+r)>>1; lc[a]=merge(lc[a],lc[b],l,mid); rc[a]=merge(rc[a],rc[b],mid+1,r); push_up(a); return a; } -
新建一个节点,把 \(a\) 和 \(b\) 合并信息存下来。
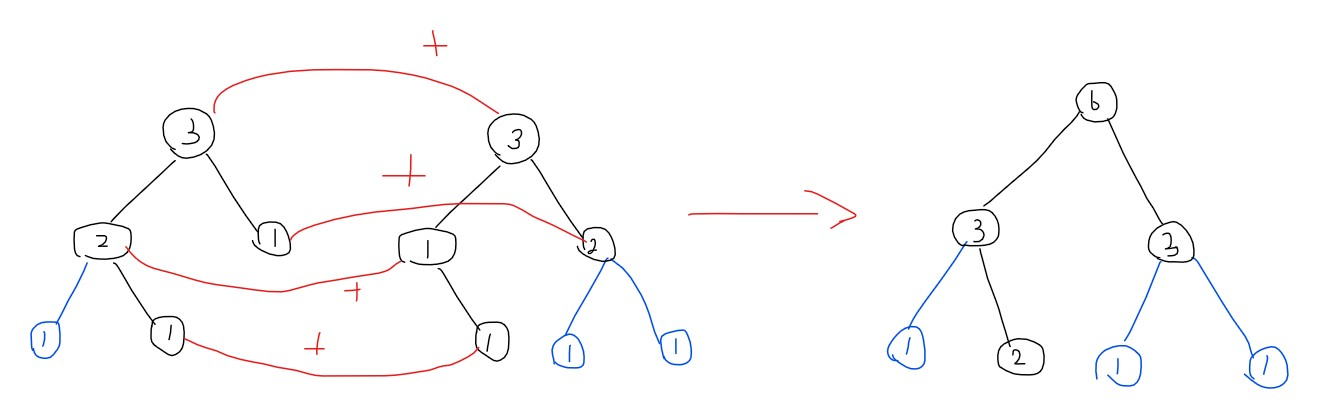
代码更好理解:int merge(int a,int b,int l,int r){ if(!a||!b) return a|b; int c=++cnt; if(l==r){ sum[c]=sum[a]+sum[b]; return; } int mid=(l+r)>>1; lc[c]=merge(lc[a],lc[b],l,mid); rc[c]=merge(rc[a],rc[b],mid+1,r); push_up(c); return c; }
例题
P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
每个节点开一个动态开点值域线段树。
离线,把修改操作在树上差分,最后一遍 dfs 从下向上用线段树合并,到一个点,把它的所有儿子的信息进行合并。
代码:
#include<bits/stdc++.h>
#define endl '\n'
#define debug(x) cerr<<#x<<':'<<x<<endl
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
using namespace std;
const int N=1e5+5,V=1e5;
int n,m;
int root[N];
int mx[N*80],pos[N*80];
int lc[N*80],rc[N*80];
int cnt;
void push_up(int p){
if(mx[lc[p]]>=mx[rc[p]]) mx[p]=mx[lc[p]],pos[p]=pos[lc[p]];
else mx[p]=mx[rc[p]],pos[p]=pos[rc[p]];
}
void ins(int &p,int l,int r,int x,int v){
if(!p) p=++cnt;
if(l==r){
mx[p]+=v,pos[p]=l;
return;
}
int mid=(l+r)>>1;
if(x<=mid) ins(lc[p],l,mid,x,v);
else ins(rc[p],mid+1,r,x,v);
push_up(p);
}
int merge(int a,int b,int l,int r){
if(!a||!b) return a|b;
if(l==r){
mx[a]+=mx[b],pos[a]=l;
return a;
}
int mid=(l+r)>>1;
lc[a]=merge(lc[a],lc[b],l,mid);
rc[a]=merge(rc[a],rc[b],mid+1,r);
push_up(a);
return a;
}
vector<int> G[N];
int fa[N],dep[N],siz[N],son[N];
int top[N],dfn[N],idx;
void dfs1(int x,int faa){
fa[x]=faa,dep[x]=dep[faa]+1,siz[x]=1;
for(int y:G[x]){
if(y==faa) continue;
dfs1(y,x);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]]) son[x]=y;
}
}
void dfs2(int x,int hd){
dfn[x]=++idx,top[x]=hd;
if(son[x]) dfs2(son[x],hd);
for(int y:G[x]){
if(y==fa[x]||y==son[x]) continue;
dfs2(y,y);
}
}
int lca(int x,int y){
while(top[x]^top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=fa[top[x]];
}
if(dfn[x]>dfn[y]) swap(x,y);
return x;
}
int ans[N];
void dfs(int x){
for(int y:G[x]){
if(y==fa[x]) continue;
dfs(y);
root[x]=merge(root[x],root[y],1,V);
}
if(mx[root[x]]) ans[x]=pos[root[x]];
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
IOS;
cin>>n>>m;
for(int i=1,u,v;i<n;i++){
cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs1(1,0),dfs2(1,1);
for(int i=1,x,y,z;i<=m;i++){
cin>>x>>y>>z;
int lc=lca(x,y);
ins(root[x],1,V,z,1);
ins(root[y],1,V,z,1);
ins(root[lc],1,V,z,-1);
if(fa[lc]) ins(root[fa[lc]],1,V,z,-1);
}
dfs(1);
for(int i=1;i<=n;i++) cout<<ans[i]<<endl;
return 0;
}