完整准确地理解 FlushHu 的题解。
0x00 初步分析
我们发现对于矩形 \(i,j\) 满足 \(h_i\leq h_j,w_i\leq w_j\),那么选 \(j\) 的时候一定可以并购 \(i\),因此将 \(i\) 删去。
将剩下的矩形按照 \(h\) 从大到小排序,此时 \(w\) 从小到大。
因为如果合并的不是一段连续区间,那么中间未被合并的部分一定可以合并。所以我们每次合并一段连续区间就好了。
设 \(f_i\) 为买下前 \(i\) 块土地的最小费用。
\[f_i=\min\{f_{j-1}+h_jw_i\} \]0x10 对函数进行分析
我们将 \(y_j=h_jw_i+f_{j-1}\) 视作一个 \(f_{j-1}\) 和 \(h_j\) 为常量,\(w_i\) 为变量 的一次函数。
事实上需要对每个 \(w_i\) 维护直线 \(y_{1\sim i}\) 上对应的值中最小的一个。
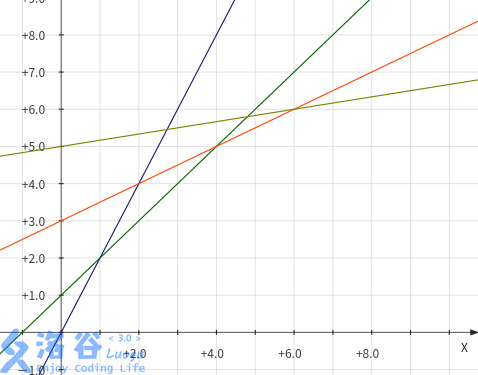
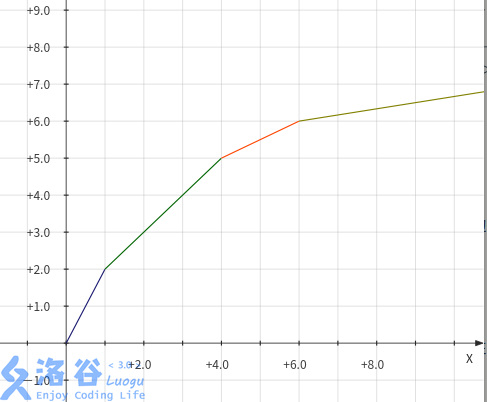
维护一个临界值 \(k\) 的单调队列。
每次加入一条直线时,斜率 \(h_j\) 递减,求得与队尾直线的临界点 \(k\)。
因为 \(w_i\) 递增,我们每次将队首临界值 \(k\leq w_i\) 的删除,队首即为最优决策。
0x11 更本质地理解斜率优化
\(f_i=\min\{h_jw_i+f_{j-1}\}\),相当于对于每个 \(j\) 有 \(f_{j-1}=-h_jw_i+t_j\),\(f_i=\min\{t_j\}\)。
我们把 \((-h_j,f_{j-1})\) 视作二维平面上一个点。
想象我们正拿着一个斜率为 \(w_i\) 的直线从下到上,遇到第一个时纵截距 \(f_i\) 取到最小值。
随便画一堆点就可以发现,无论直线以怎样的斜率向上靠,总有一些点永远都不会第一次与直线相交,也就是说这些决策是没用的。剩下的有用的决策点会构成一个凸包。
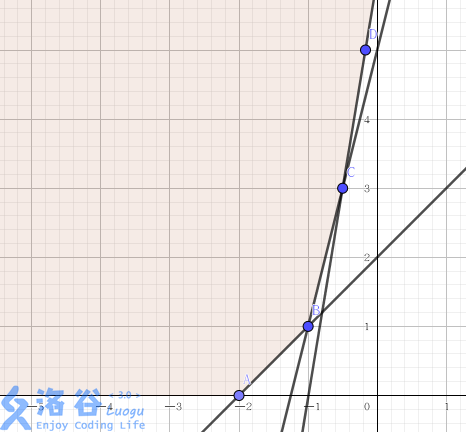
在此题中,因为 \(w\) 递增,所以我们的单调队列中存的是若干个点满足 \(-h_j\) 递增(即 \(h_j\) 递减),\(f_{j-1}\) 递增,而且相邻两个点的斜率也递增。
插入新决策点时可能会遇到下图情况:
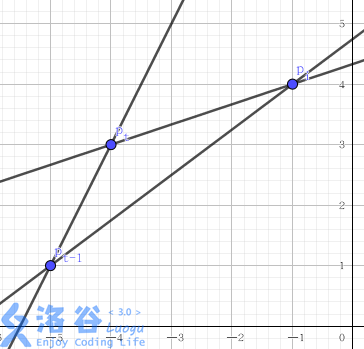
一直将队尾 \(t\) 出队,直到加入 \(i\) 后斜率仍递增。
我们再看回凸包那张图,手模一下,如果当前转移到 \(i\),一直将队首出队,直到队首和后一个的直线的斜率 \(>w_i\)。
此时队首即为能使 \(f_i\) 取得最小值的决策点。
0x12 更简单地理解斜率优化
当前以 \(i\) 结尾,有任意决策点 \(j,k\) 满足 \(1 \leq j<k\leq i\),如果 \(i\) 比 \(j\) 更优,那么必定满足:
\[f_{j-1}+h_jw_i\geq f_{k-1}+h_kw_i \]也即:
\[w_i\geq \frac{f_{k-1}-f_{j-1}}{h_j-h_k} \]\(w\) 单调递增,我们维护一个斜率 \(\frac{f_{j+2}-f_{j+1}}{h_{j+1}-h_j}\) 单调递减(即为下凸)的队列。
易证不在队列中的一定不会成为最优决策点。
0x20 总结
许多人轻易地看出了其中的玄机,但这仅仅只是日复一日的训练能够达到的吗?考场真的有足够的时间去思考吗?
当你参加比赛时,你会知道那不仅是短时间碰撞出的思维火花,更是平凡日子中对知识的深层认识和融会贯通。
正如大师所说:
题感做题就像盲人摸象,反复探索各个部位,不同局部性质难以联系,尝试很多次才能逐渐得到整体认知。而如果先知道了象的大致形态(问题的研究对象和可能的表示),再对具体的部位做研究逐步填充,局部之间是有联系的,自然探索起来事半功倍。
参考文献
[1]FlushHu. 题解 P2900[Z/OL].(2018-08-19)[2024-11-10].https://www.luogu.com.cn/article/z9eh1cp4
[2]刘承奥. 蔡德仁随笔:一些 OI 教学研究的故事[Z/OL].(2024-09-14)[2024-11-10].https://liu-cheng-ao.blog.uoj.ac/blog/9260
标签:直线,Land,leq,队首,递增,jw,Sol,斜率,P2900 From: https://www.cnblogs.com/zengzi/p/18538558