标签：连通边双 int 割点笔记 dfn low 杂题

图论系列：

前言：

もしも明日がくるのなら
あなたと花を育てたい
もしも明日がくるのなら
あなたと愛を語りたい
走って笑って転んで

相关题单：https://www.luogu.com.cn/training/641352

一.割点与桥

双连通分量是针对无向图来说的，有向图是强连通分量。在了解双连通分量之前需要先了解无向图中的割点与桥。

1.割点：

（1）定义：

割点：对于一个无向图，如果把一个点删除后这个图的极大连通分量数增加了，那么这个点就是这个图的割点（又称割顶）。

如下图中的点 2 就是一个割点，因为删去点 2 之后原图就变为 2 个连通分量了。

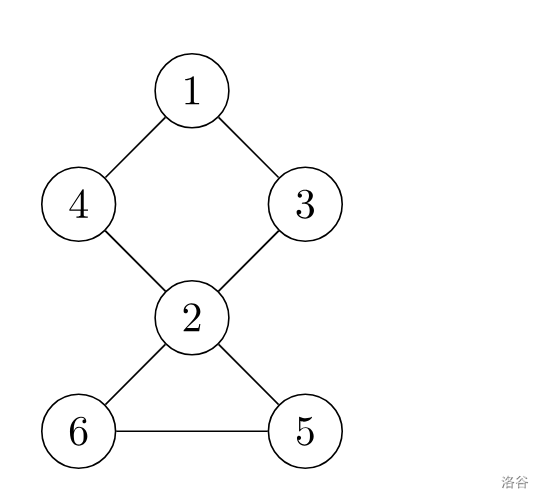
（2）求法：

一般使用 Tarjan 算法求解（因为一个一个判断时间复杂度太高了，只能利用一些性质）还是考虑同强连通一样，在无向图中跑一个 dfs 生成树，维护两个数组。

\(dfn[x]\) ：表示点 \(x\) 的 dfs 序（也就是访问的先后顺序）。

\(low[x]\)：表示满足以下条件的点的 \(dfn\) 最小值：

在 \(x\) 的子树内。
经过一条不是树边的边，能够从 \(x\) 的子树内的点到达的点。

统计出 dfn,low 数组之后，由于在一个 dfs 树内，\(dfn_x\) 始终小于等于 \(x\) 子树内的点的 dfn 值，所以判断一个点是否为割点的条件就是存在一个儿子 \(v\) 使得 \(dfn_u \leq low_v\) 。因为此时儿子 \(v\) 之下的整个子树没有边可以连接 \(u\) 子树外的点了，断开 \(u \to v\) 这条边之后，连通分量的数量必然 +1。

但是对于 dfs 生成树的起点不适用，对于 dfs 生成树的起点只需要判断其有几个不互相连通的儿子即可，只要有两个互相不连通的儿子，dfs 生成树的起点就是割点。

模板题代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=1e5+5;
int n,m,num,root;
int dfn[M],low[M];
bool vis[M];

int cnt=0;
struct N{
	int to,next;
}; N p[M<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void dfs(int u,int f)
{
	dfn[u]=low[u]=++num;//初始化dfn，low数组
	int siz=0;
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(v==f) continue;
		if(!dfn[v])
		{
			dfs(v,u),++siz;//每一次遍历到这，就说明不连通的儿子数+1，因为如果当前这个儿子与另外一个已经遍历过的儿子连通了，那么那个儿子会优先将这个点遍历，而不会留给根节点来遍历
			low[u]=min(low[u],low[v]);//儿子们能到的点，当前点也可以到达
			if(low[v]>=dfn[u]&&u!=root) vis[u]=1;//如果满足条件并且不是 dfs 生成树的根节点
		}
		else low[u]=min(low[u],dfn[v]);//经过一条不是树边的边，能够到达的 dfn 值最小的点
	}
	if(u==root&&siz>1) vis[u]=1;//特判根节点
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b),add(b,a);//无向图
	for(int i=1;i<=n;++i)
	{
		if(!dfn[i]) root=i,dfs(i,0);//没保证是个无向连通图
	}
	int ans=0;
	for(int i=1;i<=n;++i) ans+=vis[i];
	cout<<ans<<"\n";
	for(int i=1;i<=n;++i) if(vis[i]) cout<<i<<" ";
	return 0;
}

2.割边：

（1）定义：

割边：和割点差不多，叫做桥。对于一个无向图，如果删掉一条边后图中的连通分量数增加了，则称这条边为桥或者割边。

如下图中的红色的边就是割边，因为删去 \(1 \to 2\) 这条边之后原图变为两个连通分量。

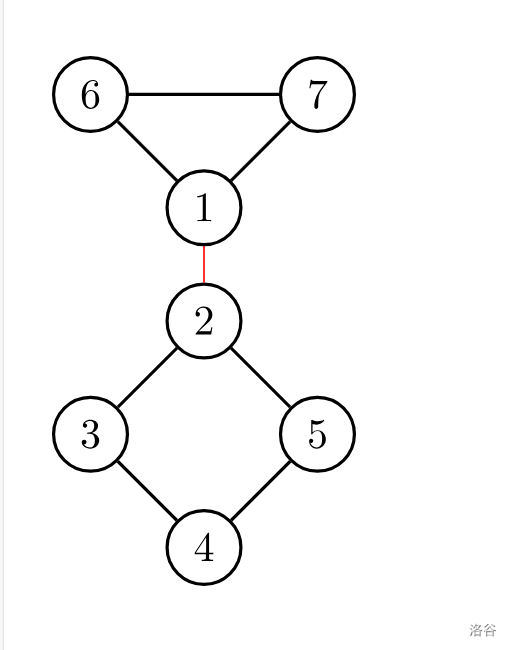
（2）求法：

和割点差不多，只要改一处：判断条件是 \(dfn_u < dfn_v\)，而且不需要考虑根节点的问题。

修改判断的理由是可能出现重边。以上图为例，如果 \(1 \to 2\) 这条边有两条，那么删去其中一条便不会增加连通分量数。但是由于是无向边，从父亲到自己有一条边，自己到父亲有一条边，既要消除这种影响，又要保留重边的影响。

那么我们对于每一条边赋一个边权 \(w\)，简单点就是记录一下当前边是第几条边，然后再 dfs 无向图的时候，记录一下当前点是由那条边转移过来的，设为 \(pre\)，如果自己有一条出边的边权与 \(pre\) 相同，就说明这是同一条边，选择跳过。

代码：

inline void tarjan(int u,int pre)
{
	dfn[u]=low[u]=++num;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(p[i].val==pre) continue;
		if(!dfn[v])
		{
			tarjan(v,p[i].val);
			low[u]=min(low[u],low[v]);
			if(low[v]>dfn[u]);//代表这条 u -> v 的边就是割边了，可能会进行一些操作，后面讲。
		}
		else low[u]=min(low[u],dfn[v]);
	}
}
//其余的同割点，不用特判根节点
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++)
	{
		cin>>a>>b;
		add(a,b,i),add(b,a,i);//给每条边赋一个边权
	}
	for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0);
	return 0;
}

二.双连通分量

1.相关定义：

边双连通：在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪条边（只能删去一条）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 边双连通。

点双连通：在一张连通的无向图中，对于两个点 \(u\) 和 \(v\)，如果无论删去哪个点（只能删去一个，且不能删 \(u\) 和 \(v\) 自己）都不能使它们不连通，我们就说 \(u\) 和 \(v\) 点双连通。

边双连通分量：对于一个无向图中的极大边双连通的子图，我们称这个子图为一个边双连通分量。

点双连通分量：对于一个无向图中的极大点双连通的子图，我们称这个子图为一个点双连通分量。

2.性质：

（1）边双连通：

一个边双连通分量内没有割边。（根据定义）

\(u,v\) 边双连通当且仅当 \(u,v\) 之间没有必经边。（根据定义）

由于边双连通分量是由一个个割边分隔开来，所以每一个点只属于一个边双连通分量。

因为每个点只属于一个边双连通分量，所以边双连通具有传递性，若 \(x,y\) 边双连通，\(y,z\) 边双连通，则 \(x,z\) 边双连通。

将每个边双连通分量缩成一个点，保留不同边双连通分量之间的边，最后会形成一颗树/森林。（因为对于无向图，去掉重边&自环之后，如果边数大于点数-1，那么必定会形成一个环，而在环上的所有点边双连通，形成一个大的边双连通分量，所以最后一定是一颗树/森林）。

图内两个之间的割边，就是两个点所在的边双连通分量代表的点，在缩完点之后形成的那颗树，两点相连经过的边。

（2）点双连通

两个点双最多只有一个公共点，且一定是割点。（根据定义，如果两个点双之间有两个公共点，那么分属两个点双的两个点就至少有一条路径分别经过这两个公共点相连，会形成一个大点双）。

若两点双有交，那么交点一定是割点。（由上面的那个性质推出）

由于点双之间具有公共点，所以点双不具有传递性。

一个点是割点当且仅当它属于超过一个点双，由一条边直接相连的两点点双连通。（根据后半句可以推出一条边恰属于一个点双，刚好同割边相反）。

对于一个点双，它在 DFS 搜索树中 dfn 值最小的点一定是割点或者树根。对于这个性质，分类讨论：

当这个点为割点时，它一定是点双连通分量的根，因为一旦包含它的父节点，他仍然是割点。
当这个点为树根时：
- 有两个及以上子树，它是一个割点。
- 只有一个子树，它是一个点双连通分量的根。
- 它没有子树，视作一个点双。

需要注意：两点之间任意一条路径上的所有割点，不一定就是两点之间的所有必经点。

3.求法：

（1）边双连通分量

由于已经知道如何求割边了，那么割边分割出来的一块块连通块就是一个个边双连通分量。类似求强连通分量，在 dfs 的时候用一个栈存下当前遍历过的点，如果判断出 \(u \to v\) 是一条割边，那么 \(v\) 子树内的点（且还没有属于其他边双）就属于一个边双，弹出栈内元素直到弹到 \(v\) 。最后由于没有到达根的边，自然也就没有割边，最后需要特殊的将所有还在栈内的元素弹出（因为可能不止根节点一个点），它们属于同一个边双。

模板题代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=2e6+5;
int n,m,num;
int low[M],dfn[M];
vector<vector<int>> ans;
stack<int> s;

int cnt=0;
struct N{
	int to,next,val;
}; N p[M<<1];
int head[M];
inline void add(int a,int b,int c)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b,p[cnt].val=c;
}
inline void push(int pos)//表示直到弹到pos才结束
{
	vector<int> res;int x;
	while(x!=pos)
	{
		res.push_back((x=s.top()));
		s.pop();
	}
	ans.push_back(res);
}

inline void tarjan(int u,int pre)
{
	dfn[u]=low[u]=++num;
	s.push(u);
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(p[i].val==pre) continue;
		if(!dfn[v])
		{
			tarjan(v,p[i].val);
			low[u]=min(low[u],low[v]);
			if(low[v]>dfn[u]) push(v);//是割边
		}
		else low[u]=min(low[u],dfn[v]);
	}
}//实质上是求割边的同时将原图分成了一个个连通块
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++)
	{
		cin>>a>>b;
		add(a,b,i),add(b,a,i);
	}
	for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0),push(i);//将剩下的点弹出
	cout<<ans.size()<<"\n";
	for(auto it:ans)
	{
		cout<<it.size()<<" ";
		for(auto x:it) cout<<x<<" ";
		cout<<"\n";
	}
	return 0;
}

（2）点双连通分量

类似边双连通分量的求法，但是略有不同。如果一个点 \(u\) 存在一个儿子 \(v\) 满足了 \(dfn_u \leq low_v\) ，那么 \(u\) 就是一个割点，这时存在一个点双连通分量含有 \(u\) 与 \(v\) 子树内还没有被分配到其他点双的点，弹出只弹出到 \(v\)，但是要将 \(u\) 也塞进这个点双里，\(u\) 由于是割点可能还属于其它的点双。

这时候不需要向求割点那样特判根节点，但是要特判单独的一个点。

模板题代码：

#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<stack>
using namespace std;
inline int max(int x,int y){return x>y?x:y;}
inline int min(int x,int y){return x>y?y:x;}
const int M=5e5+5,N=2e6+5;
int n,m,root,num;
int dfn[M],low[M];
stack<int> s;
vector<vector<int>> ans;
vector<int> res;

int cnt=0;
struct edge{
	int to,next;
};edge p[N<<1];
int head[M];
inline void add(int a,int b)
{
	++cnt;
	p[cnt].next=head[a];
	head[a]=cnt;
	p[cnt].to=b;
}
inline void push(int u,int f)//弹到 u，但是 f 点也要加进去
{
	res.clear();int x;
	while(1)
	{
		res.push_back((x=s.top()));
		s.pop();
		if(x==u) break;
	}
	res.push_back(f);
	ans.push_back(res);
}
inline void dfs(int u,int f)
{
	dfn[u]=low[u]=++num;
	s.push(u);
	int siz=0;
	for(int i=head[u];i!=0;i=p[i].next)
	{
		int v=p[i].to;
		if(v==f) continue;
		if(!dfn[v])
		{
			++siz;
			dfs(v,u);
			low[u]=min(low[u],low[v]);
			if(low[v]>=dfn[u]) push(v,u);//通过 u -> v 判断出 u 是个割点
		}
		else low[u]=min(low[u],dfn[v]);
	}
	if(!f&&!siz)//特判单点
	{
		res.clear();
		res.push_back(u),ans.push_back(res);
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);cout.tie(0);
	cin>>n>>m;
	for(int i=1,a,b;i<=m;++i) cin>>a>>b,add(a,b),add(b,a);
	
	for(int i=1;i<=n;++i)
	{
		if(!dfn[i])
		{
			while(!s.empty()) s.pop();
			root=i,dfs(i,0);//root其实没啥用
		}
	}
	cout<<ans.size()<<"\n";
	for(auto res:ans)
	{
		cout<<res.size()<<" ";
		for(int it:res) cout<<it<<" ";
		cout<<"\n";
	}
	return 0;
}

标签：连通,边双,int,割点,笔记,dfn,low,杂题
From： https://www.cnblogs.com/call-of-silence/p/18535394

双连通分量学习笔记+杂题

图论系列：

前言：

一.割点与桥

1.割点：

（1）定义：

（2）求法：

2.割边：

（1）定义：

（2）求法：

二.双连通分量

1.相关定义：

2.性质：

（1）边双连通：

（2）点双连通

3.求法：

（1）边双连通分量

（2）点双连通分量

相关文章

赞助商

阅读排行