标签：cnt 压缩 pos IFWT sum FWT 动态 规划 质数

\(3^n\)枚举子集

状压DP中相当重要的技巧（虽然后位有FWT，FMT替代，但不是都能代）

for(int i = x; i; i = (i - 1) & x) {
// i 就是 x 的子集
}

题目

P6622 [省选联考 2020 A/B 卷] 信号传递

看数据范围，\(m \le 23\)，且不同分数段增长很慢，表明会有\(O(2^m)\)的做法，考虑状压或搜索剪枝

但是题目要求的是排列的贡献，直接状压不可行，需要转化为与顺序无关的情况

观察到\(n \le 10^5\)，表明对\(S\)序列要有很快的统计方式

关键转换：发现\(s[i-1]\)到\(s[i]\)之间的转移只会有\(m^2\)种，预处理出\(s[]\)中每种的转移次数，那么此时数字\(i\)和数字\(j\)（设重排列后\(i\)在\(j\)前面）之间的贡献为：

\[W_{i,j}=cnt[i][j]*(pos[j]-pos[i])+k*cnt[j][i]*(pos[j]+pos[i]) \]

\[=pos[j]*(cnt[i][j]+k*cnt[j][i])+pos[i]*(k*cnt[j][i]-cnt[i][j]) \]

此时\(i,j\)的贡献分为两部分，分别仅与\(pos[i],pos[j]\)相关，可以分别统计；\(pos[i],pos[j]\)可以在枚举位置时分别获取，而剩下部分仅与\(i,j\)的相对位置有关，状压可以做到

方程很好推，时间复杂度\(O(m^2*2^m)\)，过不了后40分

考虑\(i\)插入时对\(S\)的影响是一定的，可以在dp外预处理出\(g[i][S]\)（想想如何做到\(O(m*2^m)\)），空间又炸了

接下来就是空间优化了 link

反思

被djy薄纱了，难受

考试时思路走错了，以为是直接替换\(s[]\)，然后关键的预处理没想到，之后应该就是自然的思路了

关键在于看到数据范围就朝着状压的方向走，不断尝试消除排列的影响

P3959 [NOIP2017 提高组] 宝藏

思路来源

读题，一眼看出状态，但发现缺少层数，无法转移

考虑强制限定层数，所有新加点强制对上一层连边，而不是任意层

感性理解该状态转移完全

p.s. 开始考虑强制选定前一个点，发现这样子树状态还要上传，有后效性，没想到是按层转移（悲

P7519 [省选联考 2021 A/B 卷] 滚榜

最朴素方程非常好列，把状态、总和，前一个数，前一个数取的值全部放入方程即可，但是没有穷举+贪心快

重要性质：由于\(b[i]\)单调不降，一个常见(?)的思路就是考虑横向统计，如图

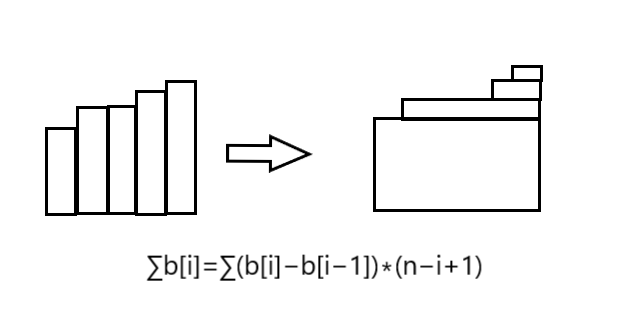
这说明我们不需要考虑前一个\(b[]\)取了多少，因为当前的\(b[]\)就是基于前面的\(b[]\)，相当于把往后的分值同时向上顶了\(b[i-1]\)，此时想要方案合法，只需考虑\(a[i]\)和\(a[i-1]\)之间差了多少即可，类似差分思想

p.s. 卡常技巧：把大循环的int变为宏会更快

根号分治

做题时，如果遇到与质因数有关的状压DP，考虑根号分治

原理：我们约定大于\(\sqrt n\)的数为大质数，则\(\forall x \in [2,n]\)，都有\(x\)的质因数中，要么没有大质数，要么有且仅有一个

这样我们就在\(x\)就唯一对应了一个大质数，利用该性质，可以解决此类问题

P2150 [NOI2015] 寿司晚宴

朴素方程略

很明显，对于一个大质数\(x\)，要么小G取，要么小W取，要么都不取，那么把所有对应此大质数\(x\)的数放在一起，分\(g1[][]\)和\(g2[][]\)分别统计\(x\)被小G取、小W取的方案数，再合并至\(f[][]\)中即可

p.s. 注意\(g1\)和\(g2\)会有重复计数（都不取），记得减掉

P8292 [省选联考 2022] 卡牌

这道题有两种做法：FWT和容斥

题解都说样例提示了正难则反，但是我觉得FWT更自然……

做法1：暴力状压+FWT优化枚举子集

先根号分治，设\(f[i][S]\)为大质数为\(i\)，小质数状态为\(S\)

对大质数不同的数分开跑\(f[i][]\)

那么最后合并答案\(f_0[S]\leftarrow \sum_{i|j=S}f_0[i]*f_k[j]\)，可以用\(FWT\)优化

做法2：容斥

看看题目要求的是什么，不要容斥错了

其实第一眼发现\(s_i\le30\)的状压是可以直接转移的，问题在于统计是枚举，考虑在这里优化

题目求的是质数集至少为\(S\)，子集反演直接pass

考虑容斥中常见的钦定大法，（不能钦定\(x\)一定出现，因为这样得到的就是题目求的质数集至少为\(S\)的方案数，绕一圈又回来了）

我们考虑钦定\(g[S]\)为\(S\)一定不出现的方案数，则\(f(S)=\sum_{T\subseteq S}(-1)^{|T|}g(T)\)

此时\(g(T)\)的贡献变得更简单：对于质数集为\(P\)的数\(x\)，若\(P\cap T=\varnothing\)，则\(x\)可被\(g(T)\)统计到，则\(g(T)=2^{cnt[T]}\)

考虑大质数时也一样，只不过对于要求选取的大质数必须选一个，即\(g(T)=2^{cnt[T]}-1\)，最后根据乘法原理把每个大质数的\(g\)乘起来即可

技巧：如果每次都把大质数的\(g\)全部累乘，那时间复杂度就会有\(O(m|S|\cdot 2^{14})\)（\(S\)为\(2000\)以内的质数集），无法承受；考虑只有给定的大质数才有必须选的需求，对于其它大质数，直接\(\sum g(T)=\sum2^{cnt[T]}=2^{\sum cnt[T]}\)计算即可，复杂度\(O(2^{14}\cdot \sum c)\)

快速沃尔什变换（FWT）

求解\(\displaystyle C_i=\sum_{j\oplus k=i}A_jB_k\)，其中\(\oplus\)为\(or,and,xor\)

FWT类似于FFT，是基于反演优化的（FWT更直观一点），实际上就是找一个式子\(FWT[A_i]=\sum A_j\)，使得\(FWT[C_i]\)恰好等于\(FWT[A_i]*FWT[B_i]\),从而用类似多项式点值表示的方法优化卷积

或卷积

这里找到的式子为\(\displaystyle FWT[A_i]=\sum_{j|i=i}A_j\)，下面是证明

\(\displaystyle FWT[A_i]*FWT[B_i]=(\sum_{j|i=i}A_j)*(\sum_{k|i=i}B_k) =\sum_{(j|k)|i=i}A_jB_k=FWT[C_i]\)

接下来就是高效处理出\(FWT[A]\)了，高维前缀和可以做到，不过考虑类似FFT的分治做法，在合并\([l,mid],[mid+1,r]\)时，有公式\(FWT[l\sim r]=merge(FWT[l\sim mid],FWT[l\sim mid]+FWT[mid+1\sim r])\)

转成二进制形式，\(A_0\)为当前最高位为\(0\)，\(A_1\)为当前最高位为\(1\)，有

\(FWT[A]=merge(FWT[A_0],FWT[A_0]+FWT[A_1])\)

还原数组时减回来即可

\(IFWT[A]=merge(IFWT[A_0],IFWT[A_0]-IFWT[A_1])\)

与卷积

\(FWT[A]=merge(FWT[A_0]+FWT[A_1],FWT[A_1])\)

\(IFWT[A]=merge(IFWT[A_0]-IFWT[A_1],IFWT[A_1])\)

异或卷积

\(FWT[A]=merge(FWT[A_0]+FWT[A_1],FWT[A_0]-FWT[A_1])\)

\(\displaystyle IFWT[A]=merge(\frac {IFWT[A_0]+IFWT[A_1]} 2,\frac {IFWT[A_0]-IFWT[A_1]} 2)\)

子集卷积

即求\(\displaystyle h(S)=\sum_{i|j=S,i\&j=\emptyset}f(i)*g(j)\)

子集反演

当方程\(f[S]\)难以快速统计转移时，考虑弱化它，然后容斥

具体地，设\(f[S]\)为状态集恰好为\(S\)时的方案数，\(g[S]\)为状态集至多为\(S\)时的方案数

即只能从\(S\)中取数，但不要求全部取完，此时\(g[S]\)的优势在于不用枚举子集，直接传\(S\)即可

此时有容斥：\(f(S)=\sum_{T\subseteq S}(-1)^{|S|-|T|}g(T)\)

证明略

P3349 [ZJOI2016]小星星

首先得想到枚举子集，向儿子递归转移，时间复杂度\(O(n^3\cdot3^n)\)

然后考虑把恰好为\(S\)换成至多为\(S\)，做子集反演，每次转移直接将\(S\)下传，将答案容斥即可

注意这里有个技巧：不需要使得编号对应不重（即树上两个点可能对应图上的同一个点），因为对于答案\(f[111...]\)，需要\(n\)个点恰好取满，这种情况必不会重

\(p.s.\) 常数优化：提取每次\(S\)的点集，还有不把\(i\)分配的编号\(q[i]\)放入递归参数（亲测快\(5\)倍，可能是开栈相对循环太慢了）

C. 拼凑数字

给你\(n\)个数字，你需要将它们拼成一个\(n\)位整数 ，使得在保证\(n\)对\(k\)取模的结果最大的前提下， 尽可能大。\(n\le 24,k\le 80\)

首先得想到朴素状压（逆天，我考时没想到

记\(f[S][i]\)为取数状态为\(S\)，余数为\(i\)的最大数，转移即可

然后想到每个数只能是\(1\thicksim 9\)，记录每种数字用了几次即可

通过计算可知，状态数最多为\(1.1\times 10^5\)，可以接受

但是对于非01串的状压，可能需要一点优化

技巧

P3813 [FJOI2017]矩阵填数

常见思路：最大值为\(v\)方案数\(=\)最大值\(\le v\)的方案数\(-\)最大值\(<v\)的方案数

但是在这里有多个矩形，直接做会有问题，因为非法方案应该是存在一个矩形最大值\(<v\)，看\(n\)的范围想到容斥

上公式：\(\displaystyle f(S)=\sum_{T\subset S}(-1)^{|S|-|T|}\cdot g(T)\)

钦定\(T\)为最大值\(<v\)的矩形集合，问题转化为快速求出\(g(T)\)

考虑离散化之后，\((x_i,y_i),(x_i+1,y_i+1)\)一定可以表示最大值限制相同的矩形，枚举离散化后的小矩形统计即可

时间复杂度\(O(n^3\cdot2^n)\)

$p.s. $ 这么好的容斥题被我浪费了，我真该死啊——

标签：cnt,压缩,pos,IFWT,sum,FWT,动态,规划,质数
From： https://www.cnblogs.com/zhone-lb/p/18522197