质数
唯一分解定理
任意一个正整数都可以唯一地表示成若干个素数的乘积,其中素数因子从小到大依次出现(这里的“乘积”可以有0个、1个或多个素因子)。
埃氏筛
要得到自然数n以内的全部素数,必须把不大于根号n的所有素数的倍数剔除,剩下的就是素数。时间复杂度\(O(nlogn)\)
a[1]=1;
for(int i=2;i*i<=n;i++)
{
if(!a[i])
for(int j=i*i;j<=n;j+=i) a[j]=1;
}
时间复杂度分析
1、
埃筛看上去有两重循环,看着好像是\(O(n^2)\)
但是分析每层循环,发现循环次数为
\[\frac{n}{1}+\frac{n}{2}+\frac{n}{3}+...+\frac{n}{n} \]\[=n(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}) \]发现括号内出现调和级数,对此有以下结论:
\[\sum^n_{i=1}\frac{1}{n}\approx \log_2n \]因此有时间复杂度\(O(n\log n)\)
2、
实际上,标准的埃筛时间复杂度为\(O(n\log \log n)\)
区别在于有无中间的 \(if(!a[i])\)
运用
埃筛常用于对因数(倍数)的筛查和统计,在数据大小支持且无法莫比乌斯反演的情况下使用
例:
70分做法:\(\displaystyle\sum^{maxa}_{i=1}\sum_{j|i}cnt[i]*cnt[j]\)
变化一下,第二维枚举倍数:\(\displaystyle\sum^{maxa}_{i=1}\sum^{maxa}_{i|j}cnt[i]*cnt[j]\)
发现符合埃筛形式,用埃筛统计即可
线性筛\(\color{red} {^*}\)
在埃氏筛中,每个数被筛若干次。
改进:使每个数只被最小质因子筛。
当循环到当前数的因子之后,即可跳出循环。
时间复杂度O(n)。
vis[0]=vis[1]=1;
for(int i=2;i<=n;i++) {
if(!vis[i]) p[++cnt]=i; //p[]记录素数
for(int j=1;j<=cnt&&i*p[j]<=n;j++) {
vis[i*p[j]]=1; //i*p[j]被p[j]筛掉
if(i%p[j]==0) break; //p[j]循环到i的最小质因数则退出,因为i*p[j]只能被
} //最小质因数筛去,也就是i的最小质因数
}
新的理解
线性筛中各种操作,相当于对当前数的分类讨论:
1、\(i\)是质数;
即 \(!vis[i]\),存入\(p[]\)
2、\(i*p[j]\)中,\(p[j]\)是\(i\)的最小质因子;
即 \(i%p[j]==0\),p[]循环边界
3、\(i*p[j]\)中,\(p[j]\)不是\(i\)的最小质因子;
正常筛数
这三类数在线性筛求各种积性函数的分析中起重要作用;
p.s.有时候需要记录最小质因子的个数;
最大公因数 & 最小公倍数
最大公因数:\(gcd(a,b)\), 亦作 \((a,b)\)
最小公倍数:\(lcm(a,b)\), 亦作 \([a,b]\)
性质
1、\(\gcd(a,b)=\gcd(b,a\!\!\mod b)\)
应用:辗转相除法求gcd,时间复杂度\(O(\log n)\)
2、\(a \times b=\gcd(a,b) \times lcm(a,b)\)
3、\(\gcd(a,b)=\gcd(b,a-b)=\gcd(a,a-b)\)
证明:设\(\gcd(a,b)=k\),则\(a=ka',b=kb'\),且\(\gcd(a',b')=1\)
\(\gcd(a,b)=k\cdot\gcd(a',b')\)
\(\gcd(b,a-b)=k\cdot\gcd(b',a'-b')\)
则问题等价于证明\(\gcd(b',a'-b')=\gcd(a',b')=1\)
反证,设\(\gcd(b',a'-b')=p\ (p\not=1)\),则有\(b'=pb'',a'-b'=p(a''-b'')\),则\(a'=pa''\),则\(\gcd(a',b')=p\),与条件矛盾,故得证
同理,第二个等号也可得出
利用此结论可以进一步证明性质1,当然还有其他用途
解题经验
多个数求gcd常用质因数分解。
例1:给定n个数,从其中选n-1个数,问最大gcd。(n <= 10^5)
解:任选两个数,答案一定在其因子里(抽屉原理)。检验答案即可。
例2:[P5502]
给定一个长度为 \(N\) 的正整数序列 \(A_i\) 。
定义权值为 \(W(L,R) = (R-L+1) × \gcd (A_l,...,A_r)\)。
求出最大权值。
\(1 \le A_i \le 10^{12}, 1 \le N \le 100000\)
解法1:cdq分治板子
解法2:考虑定住右端点时,区间\([1\thicksim l,r]\)的\(\gcd\)值最多会有\(O(\log V)\)种(\(V\)为值域)(因为根据唯一分解,区间\(\gcd\)值\(V\)在区间扩大时要么不变,要么至少缩小\(2\)倍),每次移动右端点时将这\(O(\log V)\)个值暴力修改就行了
例3: 求\(\displaystyle\sum^{i=1}_n gcd(i,k)\)
解:先对\(k\)因数分解,最多会有\(O(\sqrt k)\)的因数,再考虑这些因数的贡献,因数\(i\)的贡献可用\(n/i\)快速求出,但对于小的因数,它们的倍数也为因数时会算重,因此从大到小考虑,把大数中算重的小数容斥掉即可,时间复杂度最坏约为\(O(n^{\frac 1 2}+n^{\frac 2 3})\),但是卡不满
约数个数有关的公式,见link
例4:求\(lcm(a_1,a_2,...,a_n)\)
同余运算
基本性质
裴(péi)蜀定理
设\(a,b\)是不全为零的整数,则存在整数\(x,y\),使得\(ax+by=\gcd(a,b)\)
推论
\(a,b\)互质的充要条件是存在\(x,y\)使得\(ax+by=1\)
拓展欧几里得算法
线性不定方程
\(ax+by=c\)。给出整数 \(a,b,c\),求出一组整数解。
推导
设\(gcd(a,b)=d\)。
则若原方程有解,$c $ 必为 $ gcd(a, b)$ 的倍数(可用裴蜀定理推论证明)。
\(d=gcd(a,b)=gcd(b,a\bmod b)\),则有不定方程\(d=bx'+(a\bmod b)y'\)。
变形为:\(d=bx'+(a\bmod b)y'\)
\(\hspace{1.45cm}=bx'+(a-(a \div b)*b)*y'\)
\(\hspace{1.45cm}=bx'+ay'-(a \div b)*b*y'\)
\(\hspace{1.45cm}=ay'+b*(x'-(a \div b)*y')\)
又由于\(d=ax+by\),则有两个等式:\(x=y'\);$ y=x'-(a \div b)*y'$。
对子问题(求解\(bx'+(a\bmod b)y'=d\))进行递归直至\(b_n=0\),此时\(a_n=gcd(a,b)\),方程只剩\(a_nx_n=d\),可得此时\(x_n=1,y_n=0\)(\(y_n\)是随便赋值),回溯迭代求出\(x,y\)即可
代码
int exGcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1;y=0;
return a;
}
int r=exGcd(b,a%b,x,y);
int t=x; x=y; y=t-a/b*y;
return r;
}
时间复杂度 \(O(\log n)\)
细节处理
对于\(b \not = 0\),扩欧求出的解\(x,y\)必有\(|x| \le b,|y| \le a\)
应用
例1:[P1082]求关于x的同余方程 \(ax\equiv 1(\bmod\ b)\) 的最小正整数解。
欧拉函数
定义
正整数n的欧拉函数\(φ(n)\)的值等于不超过n且与n互质的正整数的个数。
性质

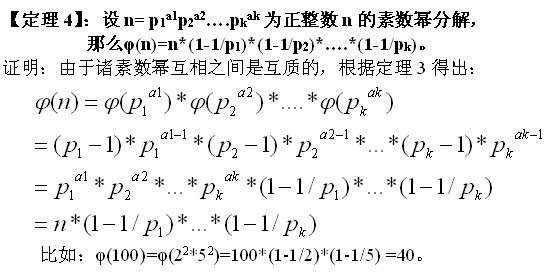
性质5: 如果p为质数,且i % p = 0,则 φ(i * p) = p * φ(i)

性质5可以用来线性求欧拉函数(欧拉筛)
代码
费马小定理
定义
假如p是质数,且gcd(a,p)=1,那么 \(a^{(p-1)} ≡1(\bmod\ p)\)
解释: 假如p是质数,且a,p互质,那么 a的(p-1)次方除以p的余数恒等于1
\(a^p≡a(\bmod\ p)\)。
欧拉定理
定义
若m,a为正整数,且\(\gcd(a,m) = 1\),则\(a^{φ(m)}≡1 (\bmod\ m)\)。
乘法逆元
扩欧求逆元

线性求逆元

中国剩余定理
求解
\[\begin{cases} x \equiv b_1\ ({\rm mod}\ m_1) \\ x\equiv b_2\ ({\rm mod}\ m_2) \\ ... \\ x \equiv b_n\ ({\rm mod}\ m_n)\end{cases} \]的\(x\)的最小正整数解,\(m_i\)两两互质
建议直接背公式
\[M=\prod_{i=1}^nm_i \]\[M_i=\frac M {m_i} \]\[ans=\sum_{i=1}^nb_iM_iM_{i \pmod {m_i}}^{-1}\pmod M \]扩展中国剩余定理
这位大佬讲得很透彻
数论分块
高效求解\(\displaystyle \sum_{i=1}^nf(i)\cdot \lfloor\frac n i\rfloor\),若\(\sum f(l\sim r)\)可以在\(O(1)\)的时间内求出,则可以在\(O(\sqrt n)\)的时间内计算该式的值
简单来说,把\(\displaystyle \lfloor\frac n i\rfloor\)相同的值一起统计即可
正确性证明
1、\(\displaystyle\lfloor \frac n i\rfloor\)的值是\(O(\sqrt n)\)的
\(i\le\sqrt n\)时,\(\displaystyle\lfloor \frac n i\rfloor\)最多\(\sqrt n\)种取值
\(i>\sqrt n\)时,\(\displaystyle\lfloor \frac n i\rfloor<\sqrt n\),\(\displaystyle\lfloor \frac n i\rfloor\)最多\(\sqrt n\)种取值
细节处理
注意\(\displaystyle\lfloor \frac{n}{\lfloor \frac{n}{i} \rfloor} \rfloor\) 有可能会超过\(n\),注意特判
例题
原根与阶
利用群论知识,可以更好理解(其实是一套东西)
定义
阶:对于整数\((a,m)=1\),满足\(a^k\equiv1\ (\bmod\ m)\)的最小整数\(k\)为\(a\)模\(m\)的阶,记作\(\delta_m(a)\)
原根:当\(\delta_m(a)=\varphi(m)\)时,\(a\)为关于\(m\)的原根
性质
1、由欧拉定理,\(\delta_m(a)\mid\varphi(m)\)
2、\(1\thicksim\delta_m(a)\)构成剩余系,\(a^1\thicksim a^{\delta_m(a)}\)互不同余,\(\delta_m(a)\)为最小循环节
3、阶的运算:
\(\delta_m(ab)=\delta_m(a)\delta_m(b)\)的充要条件为\((\delta_m(a),\delta_m(b))=1\)
\(\displaystyle\delta_m(a^t)=\frac{\delta_m(a)}{\gcd(\delta_m(a),t)}\)
证明略
4、对于原根\(g\),\(g^1,g^2,...,g^{\varphi(m)}\)构成既约剩余系
5、如果\(m\)有原根,那么\(m\)有\(\varphi(\varphi(m))\)个原根
6、由循环群的性质,\(m\)的原根一定在\(g^1,g^2,...,g^{\varphi(m)}\)之中
原根存在定理
一个数存在原根当且仅当\(m=2,4,p^{\alpha},2p^\alpha\),其中\(p\)为奇素数,\(\alpha\)为正整数
原根判定定理
\(g\)为\(m\)的一个原根的充要条件为:对于\(\varphi(m)\)的每一个质因数\(p\),都有\(\displaystyle g^\frac{\varphi(m)}{p} \not\equiv 1\ (\bmod\ m)\)
推论
若\(g\)为\(m\)的一个原根,则\(S=\{g^s|1\le s\le\varphi(m),s\perp \varphi(m)\}\)
证明:(待补充link)
求原根
1、判断是否有原根,用原根存在定理判断
2、找最小原根\(g\),已知最小原根大小不超过\(m^{0.25}\),暴力枚举,用原根判定定理判断
3、求\(g\)的\(1\thicksim \varphi(m)\)次方,\(g^s\)中\(s\perp \varphi(m)\)为原根,找出\(\varphi(\varphi(m))\)个即可
时间复杂度为\(O(m^{0.25}\log m+\varphi(m)\log \varphi(m))\)
\(p.s.\) \(998244353\)的最小原根是\(3\)
BSGS
求解\(a^x\equiv b\pmod p\),\(a\)与\(p\)互质
原理:根号平衡
设\(x=i*\lfloor\sqrt p\rfloor-j\),则有\(1\le i,j\le \lfloor\sqrt p\rfloor\)
原式化为:\(a^{i*\lfloor\sqrt p\rfloor-j}\equiv b\pmod p\)
\(a^{i*\lfloor\sqrt p\rfloor}\equiv b*a^j\pmod p\)
将\(b*a^j\)扔进map里,在遍历\(a^{i*\lfloor\sqrt p\rfloor}\)时Check就行了
时间复杂度\(O(\sqrt p\log \sqrt p)\)
拓展BSGS
即不一定满足\(a,p\)互质
考虑变形:\(a^x+kp=b\)
\(a^{x-1}\cdot a+kp=b\)
由裴蜀定理,将\(a^{x-1}\)看作\(a\)的系数,则该方程有解的充要条件是\(\gcd(a,p)\mid b\)
设\(d=\gcd(a,p)\),则\(\displaystyle a^{x-1}\cdot \frac{a}{d}+k\cdot\frac{p}{d}=\frac{b}{d}\)
然后将\(\displaystyle a^{x-1},\frac{p}{d},\frac{b}{d}\)作为新的\(a^x,p,b\) 处理
反复进行该操作,直至\(\gcd(a,p)=1\)
最后把相应系数乘上即可