专题:二次函数+圆 \(\qquad \qquad\) 题型:隐圆+轨迹 \(\qquad \qquad\) 难度系数:★★★★★
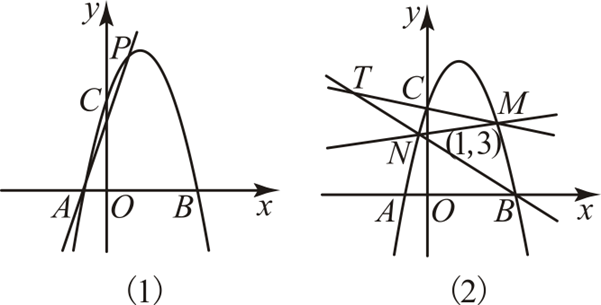
(2024年湖北模拟预测)如图,抛物线\(y=-x^2+3x+4\)与\(x\)轴分别交于\(A\),\(B\)两点(点\(A\)在点\(B\)的左侧),与\(y\)轴交于点\(C\).
(1)直接写出\(A\),\(B\),\(C\)三点的坐标;
(2)如图(1),\(P\)是抛物线上异于\(A\),\(B\)的一点,将点\(B\)绕点\(P\)顺时针旋转\(45°\)得到点\(Q\),若点\(Q\)恰好在直线上,求点\(P\)的坐标;
(3)如图(2),\(M\),\(N\)是抛物线上异于\(B\),\(C\)的两个动点,直线\(BN\)与直线\(CM\)交于点\(T\),若直线\(MN\)经过定点\(\left(1,3\right)\),求证:点\(T\)的运动轨迹是一条定直线.
【详解】(1)解:对于抛物线\(y=-x^2+3x+4\),当\(x=0\)时,\(y=4\),则\(C\left(0,4\right)\),
当\(y=0\),即\(-x^2+3x+4=0\),解得:\(x_1=-1\),\(x_2=4\)\(∴ A\left(-1,0\right),B\left(4,0\right)\).
(2)解:
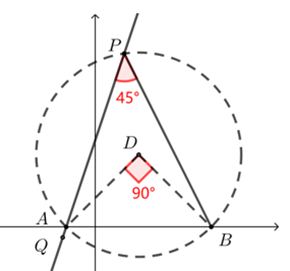
典型的“定弦定角的隐圆问题”,依题意可知,点\(P\)在以\(AB=5\)为弦,圆周角为\(\angle APB=45°\)的上,则点\(P\)为抛物线与\(\odot D\)的交点,即\(PD\)等于圆的半径.
如图所示,以\(AB\)为斜边向上作等腰直角三角形\(\triangle ABD\),

\(∵A\left(-1,0\right),B\left(4,0\right)\),则\(AB=5\),\(∴x_D=\frac{-1+4}{2}=\frac{3}{5}\),\(y_D=\frac{1}{2}AB=\frac{5}{2}\),
\(∴D\left(\frac{3}{2},\frac{5}{2}\right)\) 确定圆心\(D\)坐标和求半径.
依题意,\(\angle APB=45° =\frac{1}{2}\angle ADB\),
\(∴P\)是半径为\(\frac{5}{2}\sqrt2\)的\(\odot D\)与抛物线的交点,
设\(P\left(m,-m^2+3m+4\right)\),其中\(-1<m<4\),
\(∴\left(m-\frac{3}{2}\right)^2+\left(-m^2+3m+4-\frac{5}{2}\right)^2=\left(\frac{5}{2}\sqrt2\right)^2\),
由\(PD=r=\frac{5}{2}\sqrt2\),通过设元求点\(P\)坐标.
整理得\(\left(m+1\right)\left(m-4\right)\left(m-2\right)\left(m-1\right)=0\),解得:\(m=\pm1,2,4\),
\(∵-1<m<4\),\(∴m=1\)或\(m=2\),
则\(P\left(1,6\right)\)或\(P\left(2,6\right)\);
(3)要点1:要证“点\(T\left(m,n\right)\)的运动轨迹是一条定直线”,即只需要证明\(m,n\)存在一次函数关系或\(m,n\)其中一个是定值.
要点2:要确定动点\(T\)的轨迹,需要了解它运动的源头和它是如何产生的;
方法1 :逆向思考,动点\(T\)是直线\(NB\)和\(MC\)的交点,则可设法求出两条直线的方程,再联立便可知\(m,n\)的关系;
要求直线\(NB\)和\(MC\)方程,这可设点\(M(x_1,y_1)\)和\(N(x_2,y_2)\),由直线\(MN\)联立抛物线可知\(x_1,y_1,\ x_2,y_2\)的关系;
\(x_1,y_1,\ x_2,y_2\)表示\(m,n\)便可得到\(m,n\)的关系,确定轨迹.
方法2 :设点\(T\left(m,n\right)\),由点\(T\)和点\(C\)得到直线\(MC\)的方程,由点\(T\)和点\(B\)得到直线\(NB\)的方程;
两条直线方程分别与抛物线联立方程得到点\(M,N\)的坐标;
再利用直线\(MN\)过点\((1,3)\)得到\(m,n\)的关系从而确定轨迹.
解:设\(T\left(m,n\right)\),
\(∵B(4,0)\),\(C\left(0,4\right)\),
设直线\(TB,TC\)的解析式分别为\(y_1=k_1x+b_1\),\(y_2=k_2x+b_2\),
利用高中的直线的点斜式方程,求解会简单些.
\(\therefore\left\{\begin{array}{l} 4 k_1+b_1=0 \\ m k_1+b_1=n \end{array}\right.\),\(\left\{\begin{array}{c} b_2=4 \\ m k_2+b_2=n \end{array}\right.\),
解得:\(\left\{\begin{array}{l} k_1=\dfrac{n}{m-4} \\ b_2=\dfrac{4 n}{4-m} \end{array}\right.\),\(\left\{\begin{array}{c} k_2=\dfrac{n-4}{m} \\ b_2=4 \end{array}\right.\),
\(\therefore y_1=\frac{n}{m-4} x+\frac{4 n}{4-m}\),\(y_2=\frac{n-4}{m} x+4\)
联立\(\left\{\begin{array}{l} y_1=\frac{n}{m-4} x+\frac{4 n}{4-m} \\ y=-x^2+3 x+4 \end{array}\right.\),\(\left\{\begin{array}{c} y_2=\frac{n-4}{m} x+4 \\ y=-x^2+3 x+4 \end{array}\right.\),
消去\(y\)得:\(x^2+\left(\frac{n}{m-4}-3\right) x-4+\frac{4 n}{4-m}=0\),\(x^2+\left(\frac{n-4}{m}-3\right) x=0\),
\(\therefore x_B+x_N=3-\frac{n}{m-4}\),即\(x_N=-\frac{n}{m-4}-1\),
由\(x^2+\left(\frac{n-4}{m}-3\right) x=0\)可得\(x_M=3-\frac{n-4}{m}\),
两直线方程与抛物线联立,可求点\(M,N\)的坐标;而仅求它们横坐标会简单些,不要死求,注意到点\(B,C\)是定点,用韦达定理简单些.
依题意,直线\(MN\)的解析式为\(y=k(x-1)+3\),即\(y=kx-k+3\),
联立\(\left\{\begin{array}{c} y=k x-k+3 \\ y=-x^2+3 x+4 \end{array}\right.\),则\(x^2+\left(k-3\right)x-\left(k+1\right)=0\),
\(∴x_M+x_N=3-k\),\(x_M\cdot x_N=-k-1\),
利用韦达定理是常规手段.
\(\therefore\left\{\begin{array}{c} \left(-\dfrac{n}{m-4}-1\right)\left(3-\dfrac{n-4}{m}\right)=-k-1 \\ -\dfrac{n}{m-4}-1+3-\dfrac{n-4}{m}=3-k \end{array}\right.\),
消去\(k\)得:\(\frac{n}{m-4}+\frac{n-4}{m}+1=\left(\frac{n}{m-4}+1\right)\left(3-\frac{n-4}{m}\right)-1\),
解得:\(n=-m+4\)(与直线\(BC\)重合,故舍去)或\(n=m+8\).
即点\(T\)的运动轨迹是一条定直线\(y=x+8\).
消参\(k\)得\(m,n\)的关系式,确定动点\(T\)的轨迹.
标签:直线,begin,right,frac,函数,二次,array,初三,left From: https://www.cnblogs.com/zhgmaths/p/18470560