斜率优化初探:以 [HNOI2008]玩具装箱 为例
记 \(f[i]\) 表示装好前 \(i\) 个的最小花费。容易写出转移:
\[f[i] = \min_{j \lt i} \ [f[j]+(s[i] - s[j] - 1 - L) ^ 2] \]直接转移是 \(O(n ^ 2)\) 的,我们考虑斜率优化。
斜率优化的过程
(一)问题转化成了求最小截距。
我们把 \(min\) 的外壳去掉,并且提前把 \(L +1\) (式子更简洁) 可以得到:
\[f[i] = f[j]+(s[i] - s[j] - 1 - L) ^ 2 \]把括号打开,可以得到:
\[f[i] = f[j] + s[i] ^ 2 - 2\times s[i] \times L - 2 \times s[i] \times s[j] + (s[j] + L) ^ 2 \]移项后得到:
\[(2s[i]) \times s[j] + (f[i] - s[i] ^ 2 + 2 \times s[i] \times L) = f[j] + (s[j] +L) ^ 2 \]此时,如果我们把这看做一个一次函数,那么
\[k = 2s[i]\\ x = s[j]\\ b = (f[i] - s[i] ^ 2 + 2 \times s[i] \times L)\\ y = f[j] + (s[j] +L) ^ 2 \]注意到固定 \(i\) 后,\(k\) 是固定的。而对于每个 \(j\), 我们都可求出对应的 \((x, y)\)。此时当 \(b\) 最小时,\(f[i]\) 也会最小。
(二)截距在哪里最小?(图像理解)
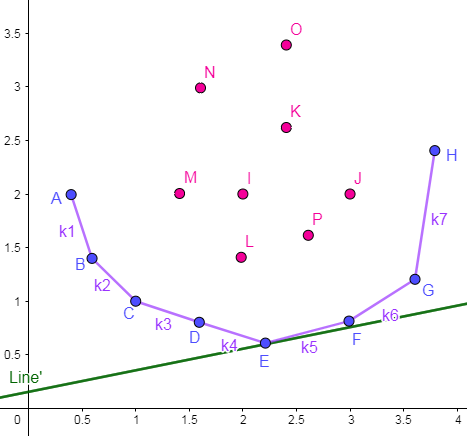
我们知道有用的 \(j\) 在二维平面上形成的点阵是个凸包。
我们惊讶的发现斜率竟然是固定的!我们可以平移这条直线至与凸包相切,显然这个切点 \(E\), 就对应着最小的截距。
怎么找这个点呢?发现 \(E\) 点以前的斜率都小于当前 \(k\), \(E\) 点之后的斜率都大于等于 \(k\), 因此可以二分这个位置。时间复杂度 \(O(nlogn)\)。
(三)决策单调性的优化(图像理解)
决策单调性的定义:
设 \(j_0[i]\) 表示 \(f[i]\) 转移的最优决策点,那么 决策单调性 可以描述为 \(\forall i \le i'\), \(j_0[i] \le j_0[i']\)。即随着 \(i\) 递增,所找到的 最优决策点 是递增态(非严格递增)。
发现 \(k = 2s[i]\), 而 \(s[i]\) 是前缀和,显然是递增的,那么我们的决策点也一定会越来越大(因为目标斜率递增)
详细证明参见参考博客。
用单调队列维护凸包的点集,分三步:
- 将斜率比目标斜率小的点弹出, 在队首位置找到最优决策点 \(j\)。
- 用最优决策点 \(j\) 更新 \(dp[i]\)。
- 把新的点加入队列中。
时间复杂度 \(O(n)\)。
#include<bits/stdc++.h>
#define F(i,l,r) for(int i(l);i<=(r);++i)
#define G(i,r,l) for(int i(r);i>=(l);--i)
#define int ll
using namespace std;
using ll = long long;
const int N = 1e5 + 5;
int L, n, h = 1, t = 0;
int f[N], s[N], q[N];
int X(int j){
return s[j] +L;
}
int Y(int j){
return f[j] + (s[j] + L) * (s[j] + L);
}
long double slope(int i, int j){
return (long double)(Y(i) - Y(j)) / (long double)(X(i) - X(j));
}
signed main(){
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> L;
++L;
F(i, 1, n) cin >> s[i], s[i] += s[i - 1] + 1;
q[++t] = 0;
F(i, 1, n){
while(h < t && slope(q[h], q[h + 1]) < 2 * s[i]) ++ h;
int j = q[h];
f[i] = f[j] + (s[i] - s[j] - L) * (s[i] - s[j] - L);
while(h < t && slope(q[t - 1], q[t]) > slope(q[t - 1], i)) -- t;
q[++ t] = i;
}
cout << f[n] << '\n';
return 0;
}
反思:移项的依据
为了用 \(Function(i)\) 表示出 \(Function(j)\),我们把含 \(i\) 的东西移到等式左边,把含 \(j\) 的东西移到等式右边。以此整理出 "不变的 \(k\),待求解的 \(b\),确定的 \(x, y\)"。 记得 \(f[i]\) 一定要放在截距 \(b\) 里面!因为我们是对 截距 求解极值。
标签:截距,为例,int,决策,long,times,斜率,HNOI2008,装箱 From: https://www.cnblogs.com/superl61/p/18452404