在上一节中,提到了分布式一致性算法的实现与多智能体之间的交流方式密切相关。这一节用图论来揭示不同多智能体之间交流方式的本质差异。
图的基本定义
我们可以将不同智能体之间的通信方式,抽象出来,称为“通信图”(graph)。
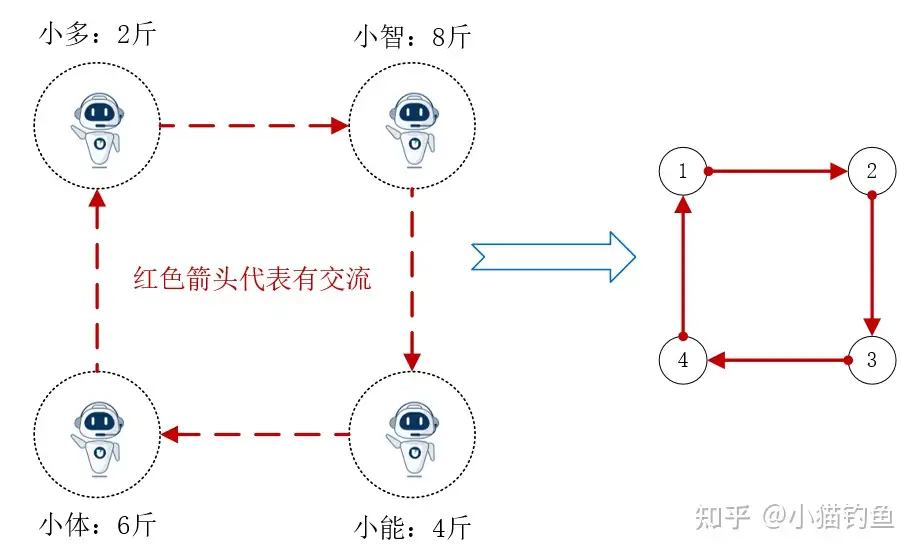
如右图所示,舍弃物理意义,将每个智能体抽象成节点(vertex)1,、2、3、4。 一张图中所有节点的集合记为: V={v1,v2,...,vN}
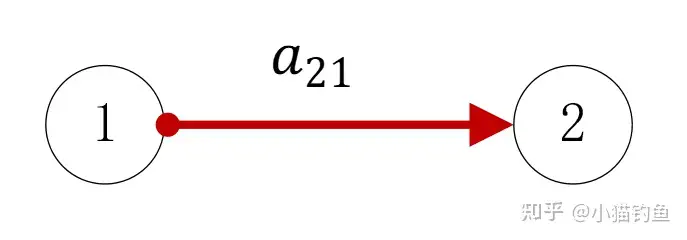
用上图中箭头表示通信方式。圆点表示尾巴(tail),箭头表示头部(head),直线表示边(edge)。可以用 e12=(v1,v2) 来表示边,它的含义是:节点1(母节点)发送信息给节点2(子节点),节点2接收来自节点1的信息。对于节点2来说,节点1就是它的邻居(neighbor)。信息在传输过程中,可能被扭曲:放大或缩小。因此在每条边上添加一个权重系数 aij ,注意,下标i为子节点,下标j为母节点,所以上图中记为 a21 。图中所有边的集合记为: E 。
对于节点 vi 来说,它可能会接收来自不同邻居(母节点)的信息,这些邻居构成节点 vi 的邻居集合: Ni={vj|(vj,vi)∈E} , |Ni| 表示节点 vi 的邻居的个数,又称为节点 vi 的入度(in-degree);同样它也会发送信息给其他节点(子节点),子节点的个数称为节点 vi 的出度(out-degree)。
如果Graph(后简写为G)中任意节点 vi 的入度和出度相等,则把G称为平衡图(balanced graph)。
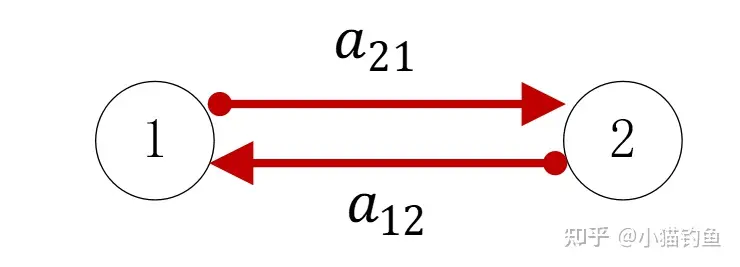
如果任意两个节点之间的通信是相互的: (vi,vj)∈E⟹(vj,vi)∈E ,如上图所示,则称G为双向图(bidirectional);否则称G为有向图(directed)。
在双向图的基础上,如果有权重系数 aij=aji ,则称G为无向图。节点之间可用一条直线连接。
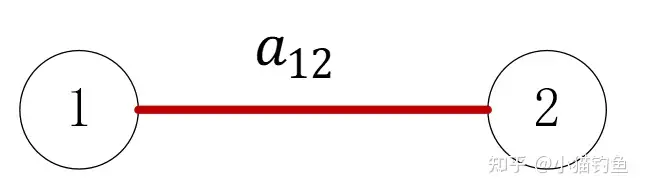
如果从某个节点出发,能够遍历所有节点,则称G有生成树(spanning tree)。有生成树是实现控制算法的必要条件。
图矩阵
一张图G的的结构和属性可以通过研究与G相关的矩阵来揭示,也就是代数图论(algebraic graph theory)。
一个N节点的G中边的权重系数 aij 可以构成一个邻接矩阵(adjacency matrix):
A=[a11a12⋯a1Na21⋱⋮⋮⋱⋮aN1aN2⋯aNN]
若 (vj,vi)∈E ,则 aij>0 ;否则 aij=0 。默认每个节点知道自己的信息,不需要和自己通信,则对角元素 aii=0 。
定义节点 vi 的加权入度(weighted in-degree)为A的第i行所有元素之和:
di=∑j=1Naij定义节点vi的加权出度(weighted out-degree)为A的第i列所有元素之和:
dio=∑j=1Naji
在文献中,通常将节点 vi 简称为节点i,并且直接使用入度、出度等概念,省略“加权”。
L矩阵
接下来介绍的拉普拉斯矩阵(Laplacian matrix),简称为L矩阵。在后续的内容中,我们将会看到L矩阵在多智能体系统中举足轻重的地位。
首先定义入度矩阵 D=diag{di} , diag{di} 表示以元素 di 作为主对角线元素的对角矩阵。
L矩阵定义为: L=D−A 。
用一个小栗子来更好的理解D矩阵和L矩阵。
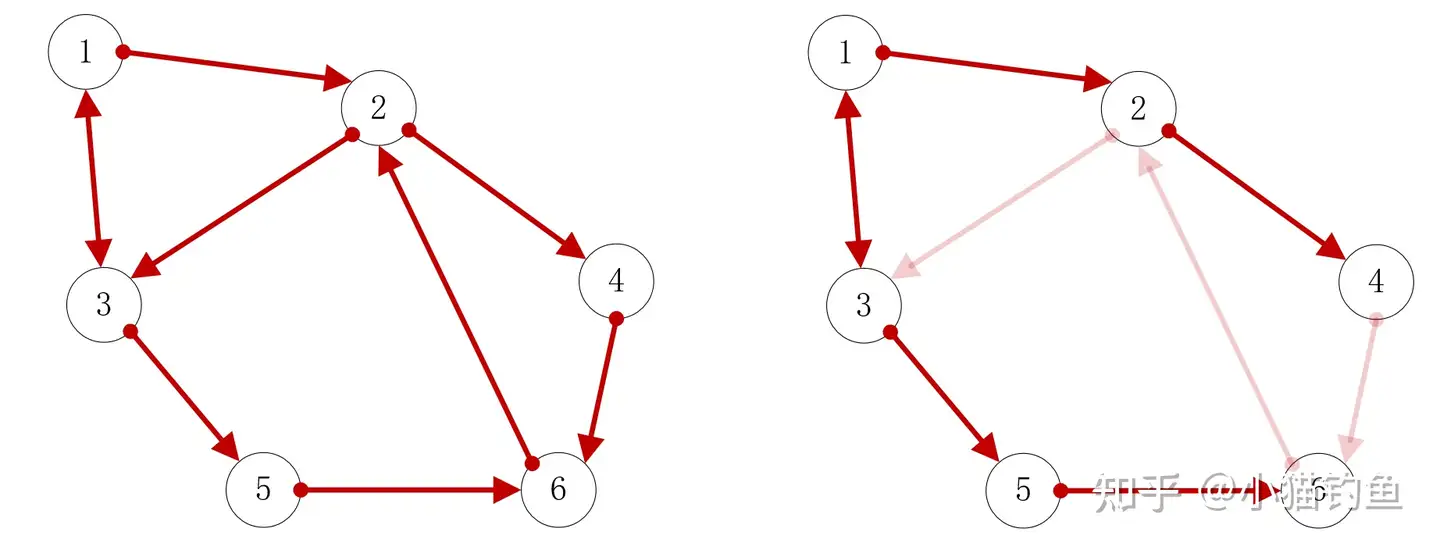
上图中一共有N=6个节点,每条边的权重系数取为1。右图显示了这个G的生成树:节点1的信息,可分别通过1-2-4和1-3-5-6传达到G中的所有节点。
G的邻接矩阵A根据图写出:
A=[aij]=[001000100001110000010000001000000110]
由于节点1只接收来自节点3的信息,因此第一行只有 a13=1 ,其余元素均为0;
节点2接收来自节点1和节点6的信息,因此第二行中, a21=1,a26=1 ,其余元素为0。其他类似写出。
根据对角入度矩阵D的定义: di=∑j=1Naij 以及 D=diag{di} ,可以得出
D=diag{di}=[100000020000002000000100000010000002]
根据定义 L=D−A ,有L矩阵:
L=D−A=[10−1000−12000−1−1−120000−1010000−1010000−1−12]
可以看出,L矩阵的每一行所有元素之和为0,即行和为0。
L矩阵的特征值与特征向量
在线性代数和矩阵论中,矩阵的特征值和特征向量都是最为核心的内容,他们在分析动态系统时至关重要。这里简单地列一下,具体的可以参考教科书。
在线性代数中,我们学过:对于一个n阶方阵L,如果它有n个相异特征根 λ1,...λn ,则一定可以找到一个矩阵P,将L对角化:
P−1LP=[λ1λ2⋱λn]
如果某个特征根有重根,则不能找到这样的矩阵P,将L对角化。
但在矩阵论中,我们又学到:如果矩阵L的所有元素都是实数,则一定可以把它化简成约当(Jordan)标准型:
J=M−1LM
M=[v1v2⋯vN] 为右特征向量组成的矩阵,特征值 λi 与特征向量 vi 满足关系:
(λiI−L)vi=0其中, I 为单位阵。
M−1=[w1Tw2T⋯wNT]T 为左特征向量组成的矩阵,特征值 λi 与特征向量 wiT 满足关系:
wiT(λiI−L)=0
其中 wiT 是标准化的,即有 wiTvi=1 。
Jordan矩阵为:
J=[λ1λ2⋱λN]
此时对角元素 λi 不是标量,而是一个Jordan块:
[λi1λi⋱⋱1λi]
很明显,Jordan标准型是更一般的矩阵对角化形式,建议仔细地阅读矩阵论的相关章节。
此处,并不进一步展开。为了便于讨论,我们假设L矩阵的特征值都是互异的,因为相应的结论容易推广到Jordan标准型下。
设L矩阵的特征值按序排列为: |λ1|⩽|λ2|⩽⋯|λN| 。对于无向图,有 L=LT ,则所有特征值都是实数,可以排列为: λ1⩽λ2⩽⋯λN 。
前面说到L矩阵的行和为0,则L1_c=0其中 1_=[1⋯1]T∈RN ,c为任意非零常数。
根据特征值的定义: (λiI−L)vi=0 ,可知L矩阵一定有一个特征值 λ1=0 ,对应的特征向量为 v1=1_c 。
定理1:如果图G有生成树,则L的秩为N-1, λ1=0 有且仅有一个,相应的右特征向量为 1_c 。
我们来看一个例子,更好地理解不同图拓扑下,L矩阵特征值的分布情况。
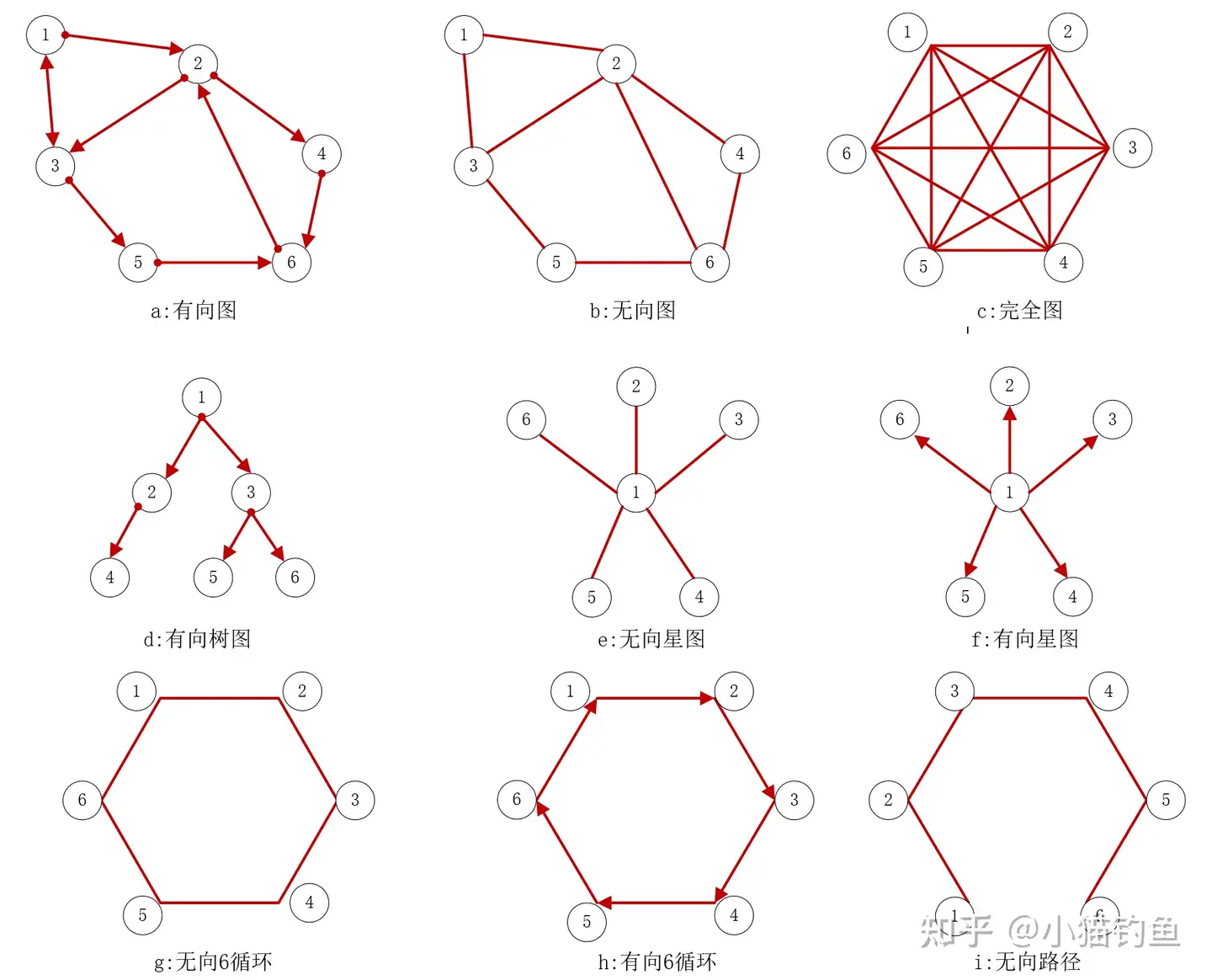
在matlab中分别计算出每幅图的L矩阵,用eig指令计算出L矩阵的特征值。
详细代码见最后。
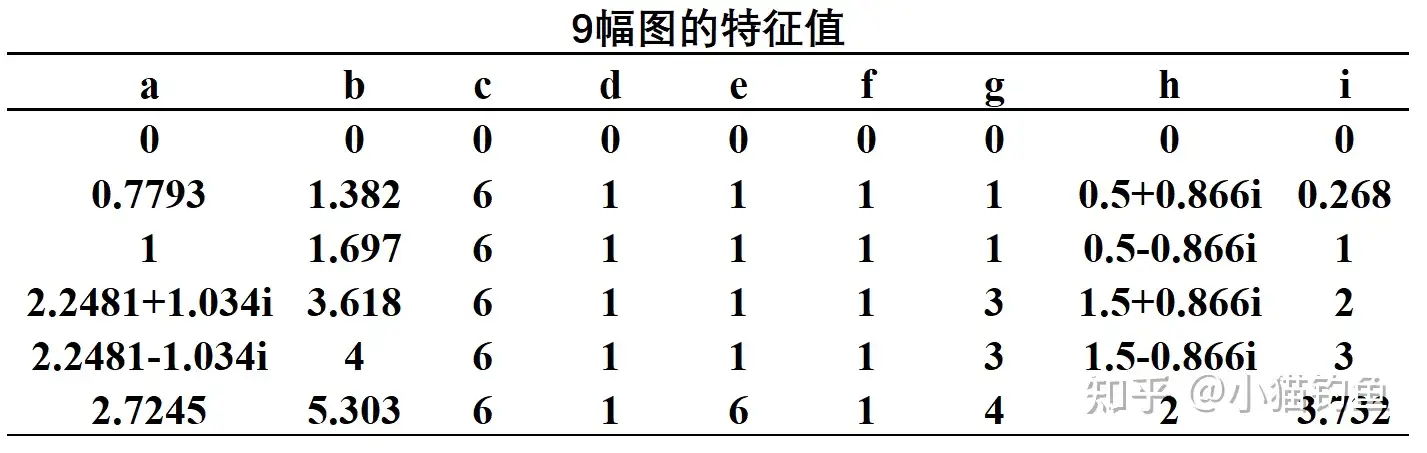
根据计算结果,可以列出9幅图的特征值为:
同样可以在复平面上绘制出特征值的分布情况,如下图:
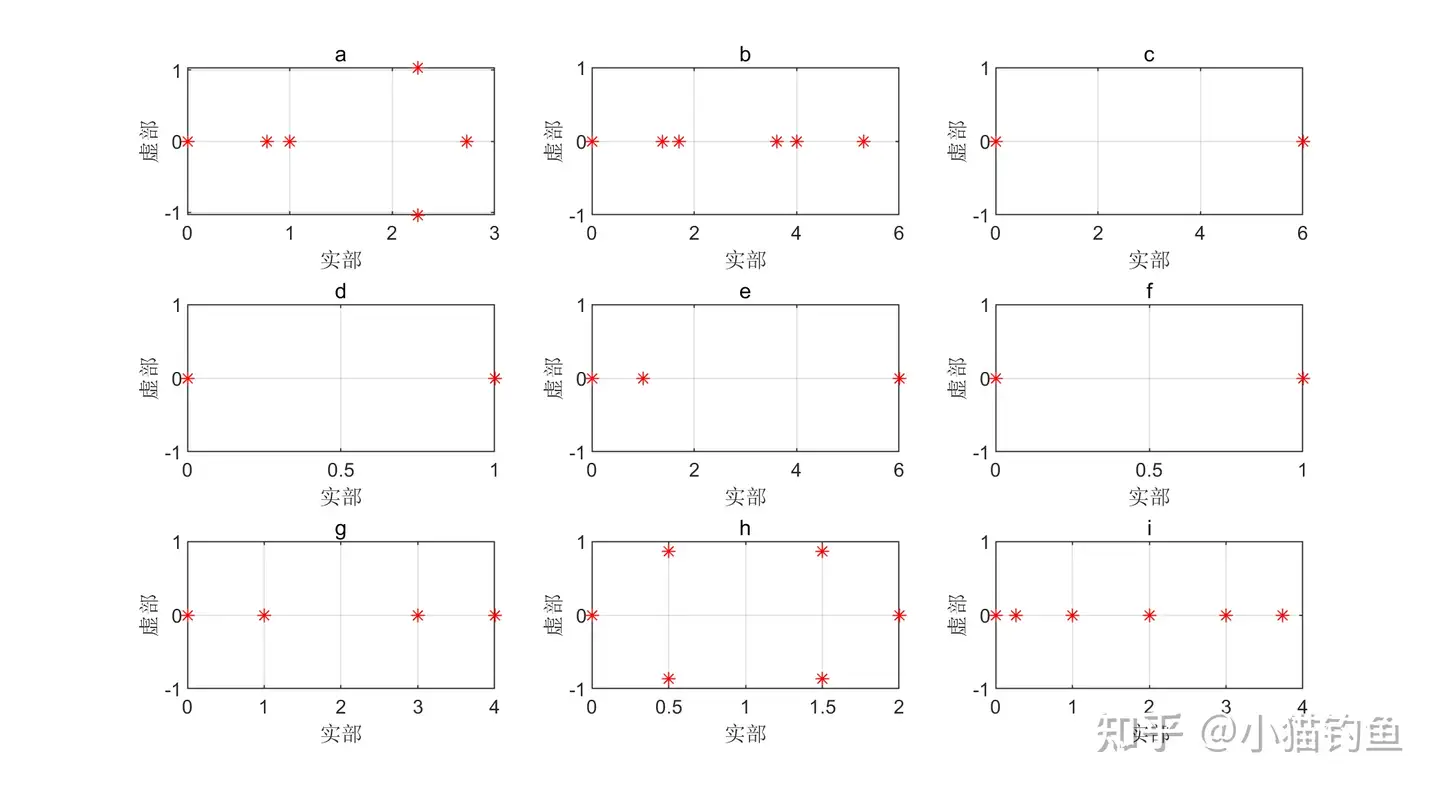
观察上表与上图,可以得出以下结论:
①由于L矩阵行和为0,所有图的第一个特征值都为0, λ1=0 ;
②对于所有无向图(b,c,e,g,i),所有特征值都是实数;
③N节点完全图(c)的所有非零特征值为 λ=N ;
④有向树(d,f)的所有非零特征值为 λ=1 ;
⑤有向N循环图的N个特征值均匀分布在以(1,0)为圆心,1为半径的圆上,且第一个特征值为0;
从下一节开始,将正式进入多智能体协同控制算法的介绍。做好面对数学疾风的准备吧。
详细代码:
clear;clc
%% 图a的特征值 L矩阵之前已经算出来了
La = [ 1 0 -1 0 0 0;...
-1 2 0 0 0 -1;...
-1 -1 2 0 0 0;...
0 -1 0 1 0 0;...
0 0 -1 0 1 0;...
0 0 0 -1 -1 2];
lambda_a = eig(La);
%% 图b的特征值
Ab = [ 0 1 1 0 0 0;...
1 0 1 1 0 1;...
1 1 0 0 1 0;...
0 1 0 0 0 1;...
0 0 1 0 0 1;...
0 1 0 1 1 0];
Db = diag(sum(Ab')); % 取转置 是因为matlab默认对矩阵按列进行求和,而我们需要对行求和
Lb = Db - Ab;
lambda_b = eig(Lb);
%% 图c的特征值
Ac = [ 0 1 1 1 1 1;...
1 0 1 1 1 1;...
1 1 0 1 1 1;...
1 1 1 0 1 1;...
1 1 1 1 0 1;...
1 1 1 1 1 0];
Dc = diag(sum(Ac'));
Lc = Dc - Ac;
lambda_c = eig(Lc);
%% 图d的特征值
Ad = [ 0 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0;...
0 1 0 0 0 0;...
0 0 1 0 0 0;...
0 0 1 0 0 0];
Dd = diag(sum(Ad'));
Ld = Dd - Ad;
lambda_d = eig(Ld);
%% 图e的特征值
Ae = [ 0 1 1 1 1 1;...
1 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0];
De = diag(sum(Ae'));
Le = De - Ae;
lambda_e = eig(Le);
%% 图f的特征值
Af = [ 0 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0;...
1 0 0 0 0 0];
Df = diag(sum(Af'));
Lf = Df - Af;
lambda_f = eig(Lf);
%% 图g的特征值
Ag = [ 0 1 0 0 0 1;...
1 0 1 0 0 0;...
0 1 0 1 0 0;...
0 0 1 0 1 0;...
0 0 0 1 0 1;...
1 0 0 0 1 0];
Dg = diag(sum(Ag'));
Lg = Dg - Ag;
lambda_g = eig(Lg);
%% 图h的特征值
Ah = [ 0 0 0 0 0 1;...
1 0 0 0 0 0;...
0 1 0 0 0 0;...
0 0 1 0 0 0;...
0 0 0 1 0 0;...
0 0 0 0 1 0];
Dh = diag(sum(Ah'));
Lh = Dh - Ah;
lambda_h = eig(Lh);
%% 图i的特征值
Ai = [ 0 1 0 0 0 0;...
1 0 1 0 0 0;...
0 1 0 1 0 0;...
0 0 1 0 1 0;...
0 0 0 1 0 1;...
0 0 0 0 1 0];
Di = diag(sum(Ai'));
Li = Di - Ai;
lambda_i = eig(Li);
%% 绘制特征值分布图
figure
hf = gcf;
hf.Color= [1 1 1]; % 控制图形的整体颜色。(scope中被默认为灰黑色,此处修改为白色)
subplot(3,3,1)
plot(real(lambda_a),imag(lambda_a),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('a')
subplot(3,3,2)
plot(real(lambda_b),imag(lambda_b),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('b')
subplot(3,3,3)
plot(real(lambda_c),imag(lambda_c),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('c')
subplot(3,3,4)
plot(real(lambda_d),imag(lambda_d),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('d')
subplot(3,3,5)
plot(real(lambda_e),imag(lambda_e),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('e')
subplot(3,3,6)
plot(real(lambda_f),imag(lambda_f),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('f')
subplot(3,3,7)
plot(real(lambda_g),imag(lambda_g),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('g')
subplot(3,3,8)
plot(real(lambda_h),imag(lambda_h),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('h')
subplot(3,3,9)
plot(real(lambda_i),imag(lambda_i),'r*')
grid on
xlabel('实部')
ylabel('虚部')
title('i')