二分图

定义

如果你能把一个图划分成两个集合，集合内部的点没有边相连接，那么这个图就是一个二分图，如图就是一个二分图：

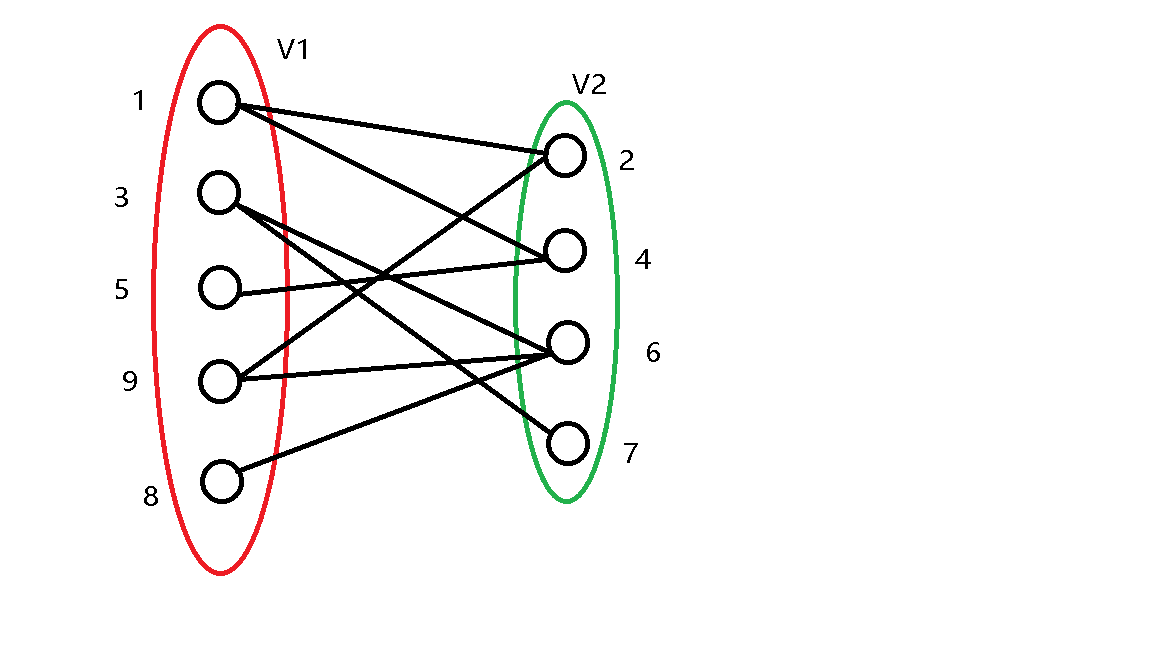
交错路：从一个没有被匹配的点出发，依次走非匹配边，匹配边，非匹配边 …… 最后到达另外一部点当中某个没有被匹配的点的路径。

增广路：从一个没有被匹配的点出发，依次走非匹配边，匹配边，非匹配边 …… 最后通过一条非匹配边到达另外一部点当中某个没有被匹配的点的路径。

性质

一个图是二分图当且仅当它不存在长度为奇数的环。

证：在二分图中，每走一条边就会切换一次集合，只有走偶数条边才可以回到原来的集合，才有可能回到原来的点，因此二分图中的环都是偶数长度的。

反过来，如果一个图只存在长度为偶数的环，那么可以对这张图黑白染色，使得一条边上的两个点颜色不同，那么将染成黑色的点分为一个集合，染成白色的点分为一个集合，就可以得到一个二分图。

这个性质可以在 \(O(|V| + |E|)\) 的复杂度内判断一个图是否是二分图。

二分图的匹配

二分图的一个匹配指的是一个边集的子集 \(E' \subseteq E\) 且 \(E'\) 中任意两条边都不存在公共顶点 (就像一个男人不会拥有两个老婆)

二分图最大匹配

对于一个二分图，他的最大匹配就是它所有匹配中边数的最大值。

匈牙利算法

匈牙利算法可以在 \(O(|V||E|)\) 的时间复杂度内求出一个二分图的最大匹配。

匈牙利算法每次枚举一个点 \(u\)，遍历和这个点连接的所有边，尝试将这个边作为匹配边去更新答案，如果这条边的另一个节点 \(v\) 没有被匹配过，那么直接匹配；如果 \(v\) 已经被匹配过了，那么尝试更改 \(v\) 的匹配边，如果 \(v\) 的匹配边可以被更改，那么就将匹配边修改，再将 \(u, v\) 之间的边标记为匹配。

举个例子：对于二分图

从 \(1\) 号点开始，直接匹配。

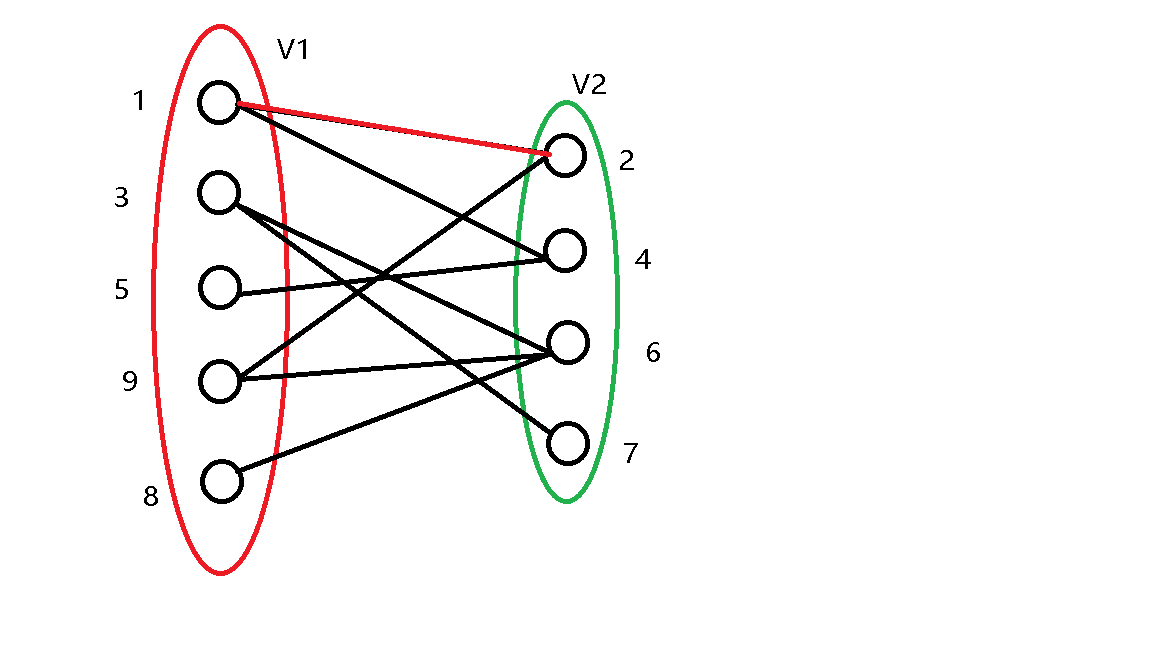
\(2\) 号点被标记过了，跳过。

\(3\) 号点也直接匹配。

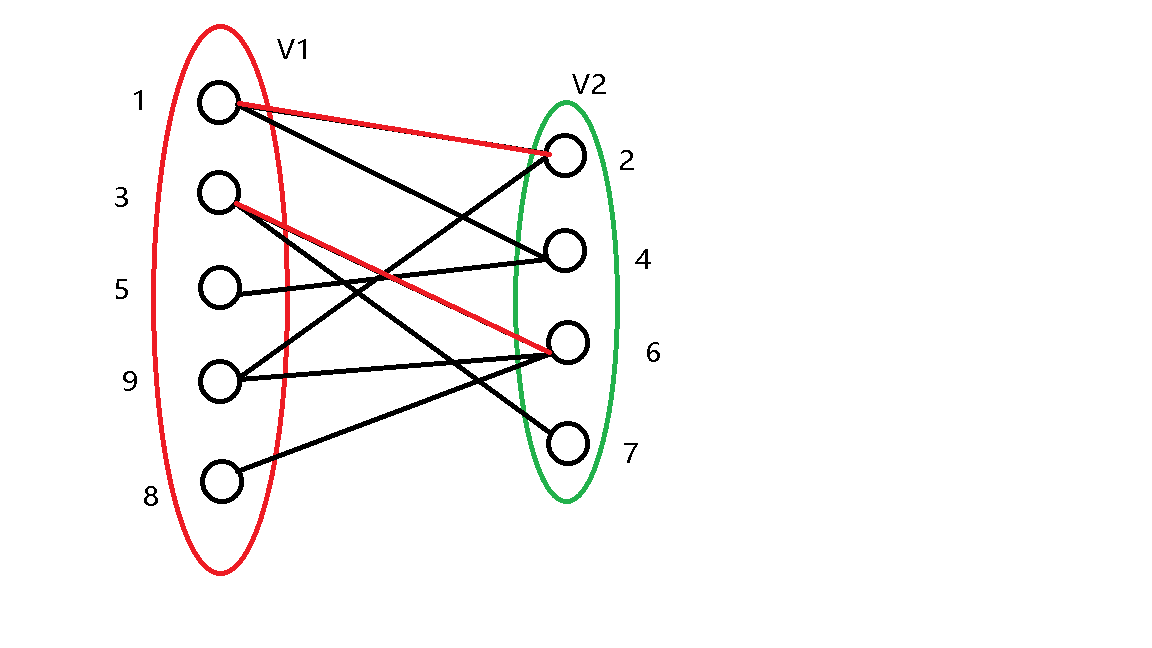
\(4\) 号点也直接匹配。

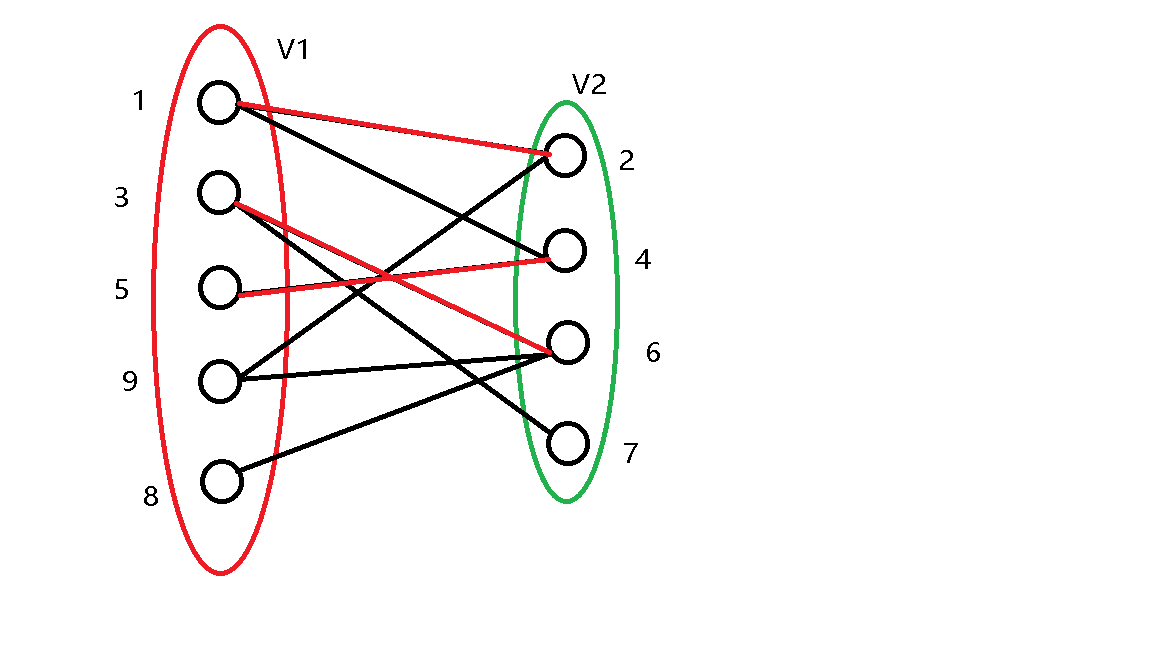
\(5\) 号点被匹配过了，跳过。

\(6\) 号点被匹配过了，跳过。

\(7\) 号点与 \(3\) 号点之间有边，尝试将这个边标记为匹配。

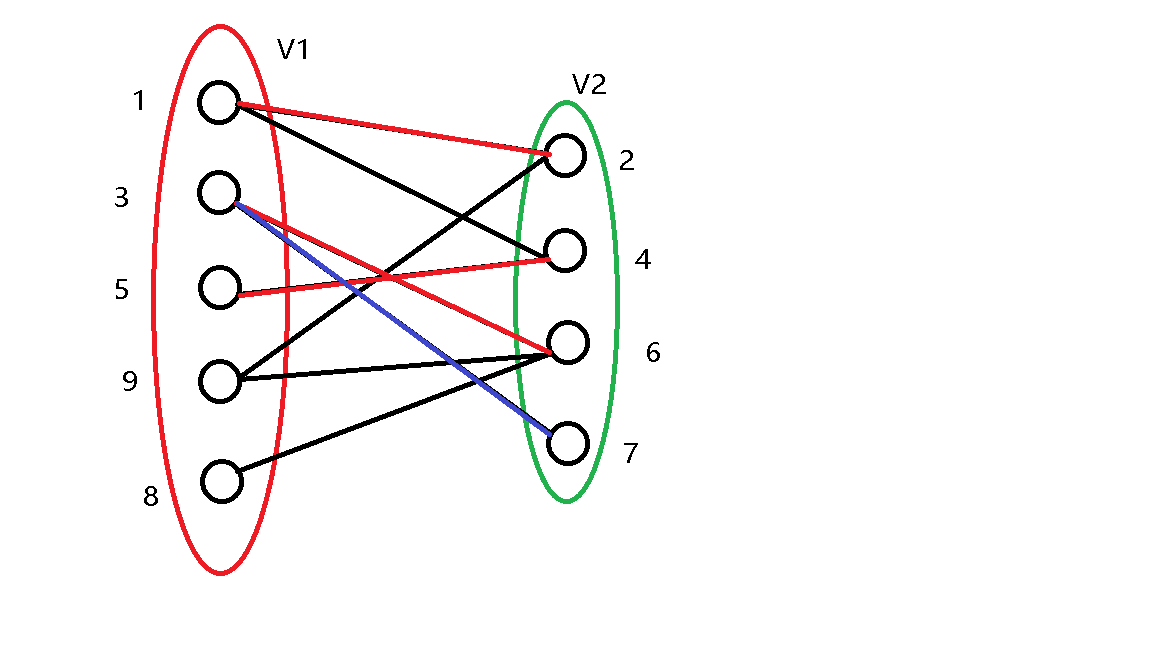
发现 \(3\) 号点已经被 \(6\) 号点匹配，继续尝试更改 \(6\) 号点的匹配，发现 \(6\) 号节点可以与 \(9\) 号点匹配，那么将 \(6\) 号和 \(9\) 号点匹配，\(3\) 号点与 \(7\) 号店匹配。

\(8\) 号点与 \(6\) 号点之间有边，尝试将这个边标记为匹配。

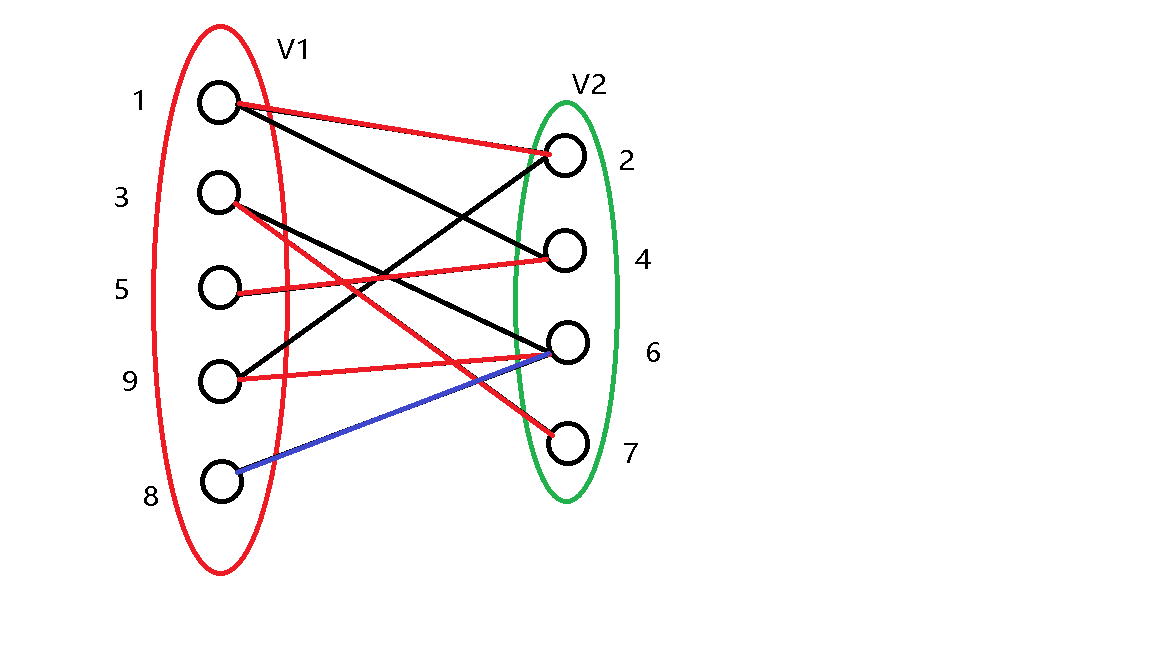
发现 \(6\) 号点已经被 \(9\) 号点匹配，继续尝试更改 \(9\) 号点的匹配。

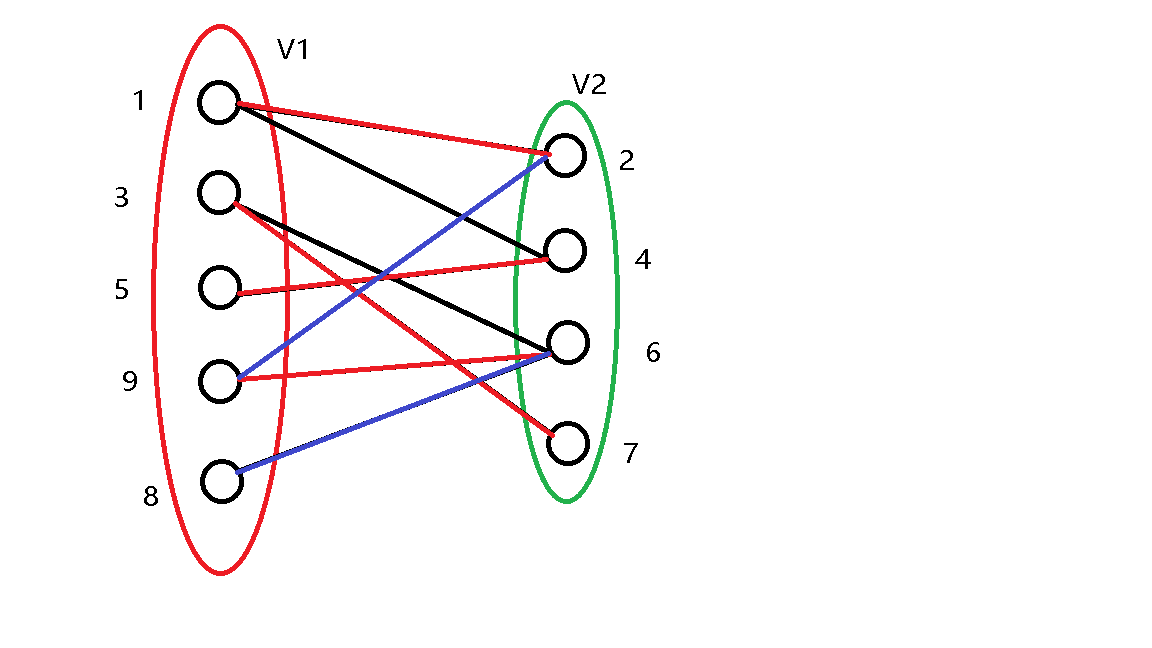
发现 \(2\) 号点已经被 \(1\) 号点匹配，继续尝试更改 \(1\) 号点的匹配。

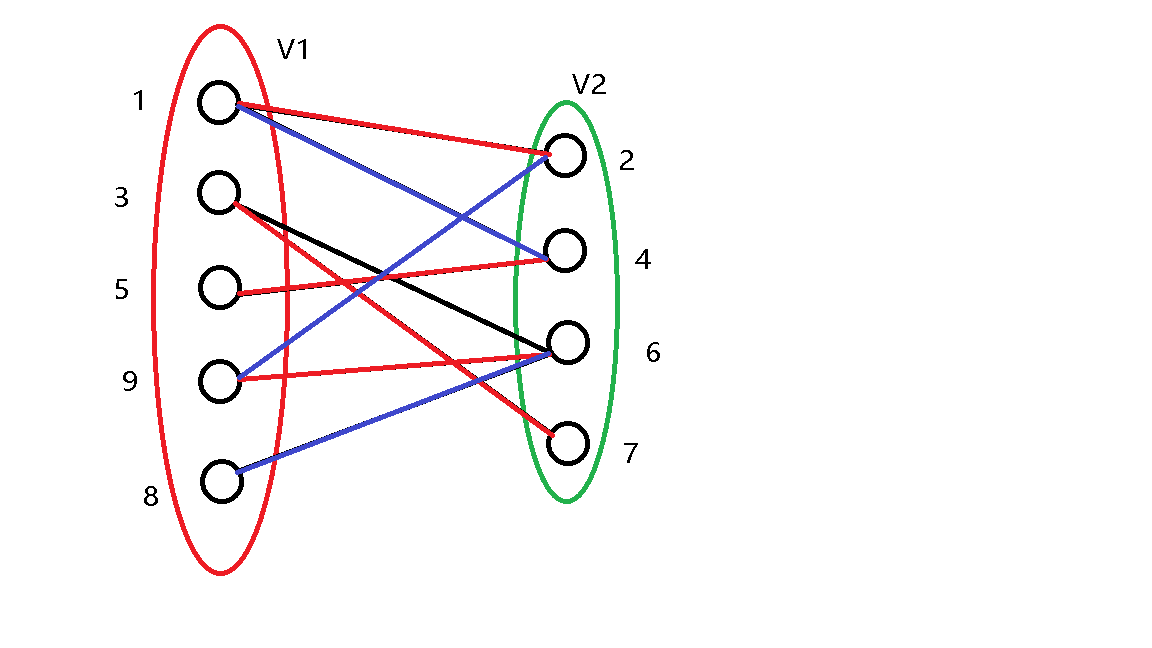
发现 \(4\) 号点已经被 \(5\) 号点匹配，继续尝试更改 \(5\) 号点的匹配，发现 \(5\) 号点无法更改匹配，说明本次尝试无法更改匹配。

\(9\) 号点被匹配过了，跳过。

这样就得出了最终匹配：

可以发现：此过程相当于对每个点寻找它的增广路，，然后切换所有边的匹配状态，以此增加匹配数。

完整代码：P3386 【模板】二分图最大匹配

#include<bits/stdc++.h>
using namespace std;
int G[510][510];
int match[510], reserve_boy[510];//match[i]表示i号点的匹配对象（图上红边），reverse_boy[i]表示尝试匹配中i号点是否被匹配（图上蓝边）
int n, m;
bool dfs(int x){
	for(int i = 1; i <= m; i++)
		if(!reserve_boy[i] && G[x][i]){
			reserve_boy[i] = 1;//这个点标记为被匹配
			if(!match[i] || dfs(match[i])){//这个点没被匹配货可以更改匹配
				match[i] = x;//更新匹配
				return true;
			}
		}
	return false;
}
int main(){
	int e;
	scanf("%d%d%d", &n, &m, &e);
	while(e--){
		int a, b;
		scanf("%d%d", &a, &b);
		G[a][b] = 1;
	}
	int sum = 0;
	for(int i = 1; i <= n; i++){
		memset(reserve_boy, 0, sizeof(reserve_boy));
		if(dfs(i))
			sum++;
	}
	printf("%d\n", sum);
	return 0;
}

最大流算法

讲到最大流时会讲，此处不做阐述。

二分图完美匹配

对于一个二分图，如果它的两个点集点数相等且他的最大匹配数量等于任意一个点集大小，那么就称这是这个二分图的一个完美匹配。

二分图最大权完美匹配

KM 算法

匈牙利算法可以在 \(O(|V| ^ 4)\) 的时间复杂度内求出一个二分图的最大权完美匹配。

先来两个定义：

• 可行顶标：给每个点赋值一个点权 \(l_u\)，满足 \(\forall (u, v) \in E\)，\(w_{u, v} \leq l_u + l_v\)

• 相等子图：原图的一个生成子图，包括了原图所有的点，包含且仅包含满足 \(w_{u, v} = l_u + l_v\) 的边 \((u, v) \in E\)

定理1.3.1

对于某组可行顶标，如果根据这组可行顶标构造的相等子图存在完美匹配，那么，该匹配就是原二分图的最大权完美匹配。

证：考虑任意一组完美匹配 \(M\)，其边权和为：\(\displaystyle\sum_{(u, v) \in M}w_{u, v} \leq \sum_{(u, v) \in M} l(u) + l(v)\) (可行顶标的定义) \(= \displaystyle\sum_{u \in V} l(u)\) (二分图完美匹配的定义)

而这个相等子图的完美匹配的边权和为 \(\displaystyle\sum_{u \in V} l(u)\)，因此一定是最大权完美匹配。

于是现在问题变成了调整可行顶标，使得相等子图存在完美匹配。

初始时我们随便给所有顶点一个可行的可行顶标(一般设 \(l_u = \operatorname{max}_{1 \leq j \leq n}w_{i, j}, l_v = 0\))。然后每次选出左部点中第一个没有匹配的点，遍历所有从它出发的在相等子图中的交错路，如果存在增广路就将增广路上的所有边切换匹配状态。

否则记左部点中在交错路中的集合为 \(S_1\)，没在的为 \(S_2\)，右部点的为 \(T_1\) 和 \(T_2\)。

那么在相等子图中的边有如下的事实：

• 不存在 \(S_1 \rightarrow T_2\) 的边，否则从 \(S_1\) 中的点出发的交错路会到达 \(T_2\) 中的点。

• 如果存在 \(S_2 \rightarrow T_1\) 的边，那一定不是匹配边，否则这个 \(S_2\) 中的点应该属于 \(S_1\)

现在开始协调调已经有匹配的左部点的顶标，我们考虑给 \(S_1\) 的所有点的顶标减去一个数 a，给 \(T_1\) 的所有点的顶标加上 a。那么有：

• \(S_1 \rightarrow T_1\) 的边不会变化，因为它们中的点在交错路上，满足 \(l_u + l_v = w_{u, v}\)

• \(S_2 \rightarrow T_2\) 的边不会变化，因为它们的可行顶标没有发生变化。

• \(S_1 \rightarrow T_2\) 的边可能加入相等子图，因为 \(l_u\) 减小，\(l_v\) 不变，\(l_u + l_v\) 减小。

• \(S_2 \rightarrow T_1\) 的边不可能加入相等子图，因为 \(l_u\) 不变，\(l_v\) 增大，\(l_u + l_v\) 增大。

因此我们要让 \(S_1 \rightarrow T_2\) 中的最大的边恰好加入相等子图，即：\(a = \operatorname{min}_{u \in S_1, v \in S_2}{l_u + l_v - w_{u, v}}\)

对 \(T_1\) 中的每个点 \(v\) 维护 \(slack_v = \operatorname{min}_{u \in S_1}{l_u + l_v - w_{u, v}}\)，那么每次修改顶标后可以通过 \(a = \operatorname{min}_{v \in T_2}slack_v\) 更新 \(a\)

这个协调的过程最多进行 \(|V|\) 次就可以找到一条增广路。于是朴素维护的复杂度为 \(O(|V| ^ 4)\)

采用DFS，就是最朴素的写法。

举个例子：对于二分图

完整代码：P6577 【模板】二分图最大权完美匹配

#include<bits/stdc++.h>
using namespace std;
#define int long long 
const int N = 5e2 + 9, M = 3e5 + 9, inf = 0x3f3f3f3f3f3f3f3f;
int w[N][N], slack[N];
int lx[N], ly[N];
bool visx[N], visy[N];
int matx[N], maty[N], pre[N], n, m;
queue <int> q; 
bool check(int x){
	visy[x] = 1;
	if(maty[x]){
		q.push(maty[x]);
		return false;
	}
	while(x){
		maty[x] = pre[x];
		int t = matx[pre[x]];
		matx[pre[x]] = x;
		x = t;	
	}
	return true;
}
bool bfs(){
	while(!q.empty()){
		int u = q.front();
		q.pop();
		if(visx[u])
			continue;
		visx[u] = 1;
		for(int v = 1; v <= n; v++){		
			if(w[u][v] != -inf){
				if(visy[v])
					continue;
				if(lx[u] + ly[v] - w[u][v] < slack[v]){
					slack[v] = lx[u] + ly[v] - w[u][v];
					pre[v] = u;
					if(!slack[v] && check(v))
						return true;
				}
			}
		}
	}
	int delta = inf;
	for(int i = 1; i <= n; i++)
		if(!visy[i])
			delta = min(delta, slack[i]);
	for(int i = 1; i <= n; i++){
		if(visx[i])
			lx[i] -= delta;
		if(visy[i])
			ly[i] += delta;
		else
			slack[i] -= delta; 
	}	 
	for(int i = 1; i <= n; i++)
		if(!visy[i] && !slack[i] && check(i))
			return true;
	return false;
}
int KM(){
	for(int i = 1; i <= n; i++){
		lx[i] = -inf;
		for(int j = 1; j <= n; j++)
			lx[i] = max(lx[i], w[i][j]);
	}
	for(int i = 1; i <= n; i++){
		memset(slack, 0x3f, sizeof(slack));
		memset(visx, 0, sizeof(visx));
		memset(visy, 0, sizeof(visy));
		while(!q.empty())
			q.pop();
		q.push(i);
		while(!bfs());
	}
	int ret = 0;
	for(int i = 1; i <= n; i++)
		ret += w[maty[i]][i];
	return ret; 
}
signed main(){
	scanf("%lld%lld", &n, &m);
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++)
			w[i][j] = -inf;
	for(int i = 1; i <= m; i++){
		int u, v, x;
		scanf("%lld%lld%lld",&u, &v, &x);
		w[u][v] = max(w[u][v], x);
	}
	printf("%lld\n", KM());
	for(int i = 1; i <= n; i++)
		printf("%lld ", maty[i]);
	return 0;
}

费用流算法

讲到费用流时会讲，此处不做阐述。

二分图的应用：最小点覆盖

定义：对于一张二分图，它的点覆盖是一个点集的子集，满足每条边都恰好有一个顶点在这个子集中。

它的最小点覆盖则是所有点覆盖中集合大小最小的点覆盖。

定理1.4.1

对于一张二分图，其最大匹配数等于其最小点覆盖数。

证：考虑如果存在完美匹配则显然。否则设已经有了一个匹配且右部点没有全部匹配，
然后从右边的每个非匹配点出发找增广路，把经过的所有节点标注出来，如图：

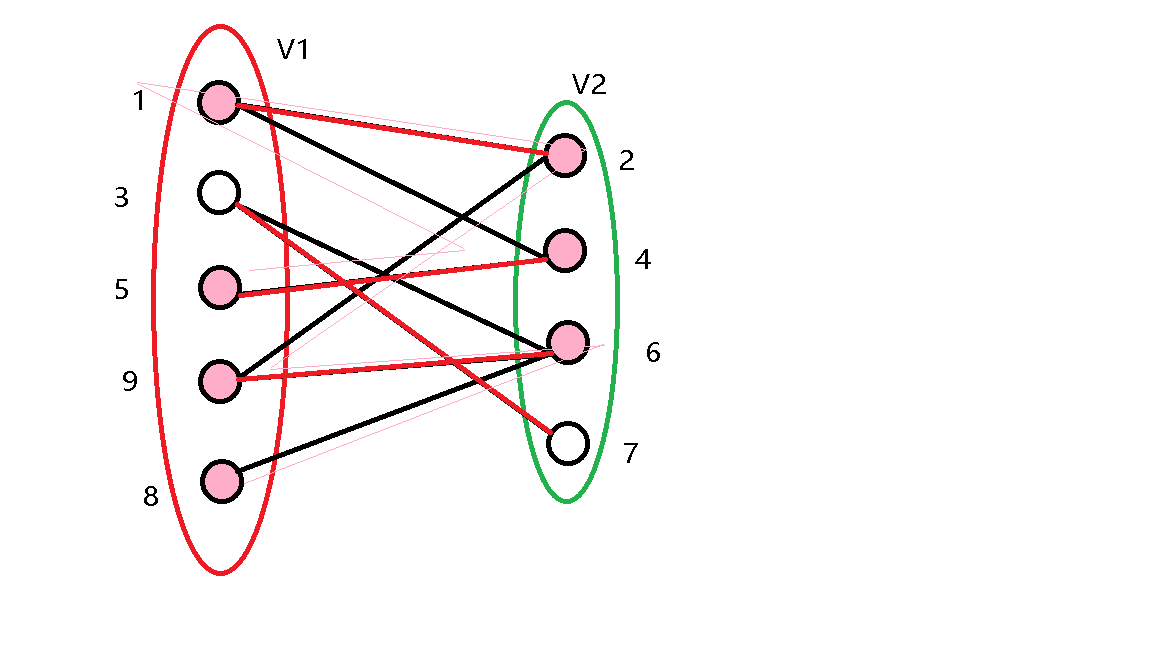(粉色细线为增广路)

这时候我们把右部点中没有被标记的点拿出来，左部点被标记的点拿出来。

分别考虑左部点和右部点。对于左部点：如果它不是匹配点，那么找到了一条增广路，匹配可以增大；对于右部点：如果它不是匹配点，那么一定会从它出发寻找非匹配边。

\(\therefore\) . 所有拿出来的点都是匹配点。

再次是分别考虑左部点和右部点。考虑右边的标记点连出来的边，假设它左边的点没有标记(那么该右部点一定是匹配点)，那么有两种情况：

• 该点不是匹配点：那么这条边一定不是匹配边，于是可以加入交错路，左部点不可能不标记.

• 该点是匹配点：那么这条边一定是匹配边，但是这样右部点就不可能被标记

左部点的情况同理。

\(\therefore\) 拿出来的点构成一个点覆盖。

覆盖所有匹配边就至少需要这么多点。
至此，我们证明了最大匹配等于最小覆盖，并给出了一种可行的构造方案。

二分图的应用：最大独立集

定义：对于一张二分图，那些没有边直接的顶点组成的集合。

它的最大独立集则是所有独立集中集合大小最大的独立集。

定理1.5.1

对于一张二分图，其最大点独立集数 \(U\) 等于其总点数减去最大匹配数 \(M\) 。

证：考虑把最小点覆盖的点全部去掉一定构成一个独立集，也即 \(U \geq n − M\)

另一方面，所有匹配里面最多选择一个点，也即 \(U \leq n − M\)，于是有 \(U = n − M\)

网络流

网络的基本概念

网络是指一种特殊的有向图 \(G = (V, E)\)，其与一般有向图的不同之处在于有容量和源汇点。

\(E\) 中每条边 \((u, v)\) 都有一个被称为容量的权值 \(c_{u, v}\)，对于 \((u, v) \not \in E\)，可以设 \(c_{u, v} = 0\)

\(V\) 中有两个特殊的点：源点(\(s\))，汇点(\(t\))(\(s \neq t\))

流是一个从有序数对 \(u, v\) 映射到实数域 \(\mathbb{R}\) 的函数 \(f(u, v)\)

网络的性质

参考资料

• 二分图最大匹配 OI Wiki

• 二分图最大权匹配 OI Wiki

• Bipartite+graph 校内课件

• 网络流，二分图与图的匹配 Alex_wei

• 图论——二分图——最小点覆盖 Probie Tao

• 二分图知识点：一篇笔记带你回顾 Hacking Group 0318