首页 > 其他分享 >2024.8.30校测

2024.8.30校测

时间：2024-09-20 17:16:06浏览次数：1  
标签：输出 return leq 2024.8 校测 30 样例 int dp

T1

题目描述

物理老师 YJ 有一个长杆天平，天平的两臂长均为 \(15\)，将长杆看作 \(x\) 轴，则平衡点在 \(0\) 位置处，负数位置在左臂上，正数位置在右臂上。长杆上有 \(n\) 个位置有挂钩可以挂秤砣。YJ 有 \(m\) 个秤砣，质量分别为 \(g_i\)，每个挂钩可以不挂也可以挂任意个秤砣。YJ 想要知道，在使用所有秤砣的条件下，有多少种不同的挂秤砣的方案，可以使得天平平衡？问题太过复杂，仅凭物理知识难以解决，所以请你来帮助他。

天平的平衡条件是所有秤砣的位置质量之和为 \(0\)。例如有质量为 \(2,3,4\) 的秤砣分别挂在 \(-3,-2,3\) 位置处，则 \(2 \times (-3) + 3 \times (-2) + 4 \times 3 = 0\)，天平是平衡的。

输入格式

第一行两个数 \(n, m\)。表示挂钩的数目和秤砣的数目。

第二行 \(n\) 个不同且递增的数，第 \(i\) 个数表示第 \(i\) 个挂钩的位置，数的范围在 \([-15,15]\) 内。

第三行 \(m\) 个不同且递增的数，第 \(i\) 个数表示第 \(i\) 个秤砣的质量，数的范围在 \([1,25]\) 内。

输出格式

一个整数，代表能使得天平平衡的方案数。

输入样例

2 4
-2 3
3 4 5 8

输出样例

2

样例解释

方案 \(1\)：\((-2) \times (3 + 4 + 5) + 3 \times 8 = 0\)。

方案 \(2\)：\((-2) \times (4 + 8) + 3 \times (3 + 5) = 0\)。

数据规模

对于 \(10\%\) 数据，\(2 \leq n, m \leq 4\)。

对于 \(100\%\) 数据， \(2 \leq n, m \leq 20\)。

题解

考虑可以组合出的重量在 \(-7500\) 到 \(7500\) 之间，我们可以枚举这个重量，把这个重量作为容量，再用背包做就行了。

完整代码

#include <bits/stdc++.h>
using namespace std;
#define int long long 
const int N = 1.5e4 + 9, M = 39;
int dp[M][N], w[N], p[N], n, m;
signed main(){
	freopen("balance.in", "r", stdin);
	freopen("balance.out", "w", stdout);
	scanf("%lld%lld", &n, &m);
	for(int i = 1; i <= n; i++)
		scanf("%lld", &p[i]);
	for(int i = 1; i <= m; i++)
		scanf("%lld", &w[i]);
	dp[0][7500] = 1;
	for(int i = 1; i <= m; i++)
		for(int j = 1; j <= n; j++)
			for(int k = 0; k <= 15000; k++){
				if(k - w[i] * p[j] < 0 || k - w[i] * p[j] > 15000)
					continue;
				dp[i][k] += dp[i - 1][k - w[i] * p[j]];
			}
	printf("%lld", dp[m][7500]);
	return 0;
}

T2

题目描述

山峰数是指数字排列中不存在山谷（先降后升）的数，例如 \(0, 5, 13, 12321\) 都是山峰数，\(101, 1110000111\) 都不是山峰数。

现给出 \(n\) 个数，请依次判断它们是否为山峰数，如果不是，输出 -1。如果是，求出比它小的数中有多少个山峰数。

输入格式

第一行一个数 \(n\)，表示询问数目。

接下来 \(n\) 行，每一行一个数 \(x\)，表示询问的数。

输出格式

输出有 \(n\) 行，\(x\) 如果不是山峰数，输出 -1。\(x\) 如果是山峰数，则输出有多少个比它小的山峰数。

输入样例

5
10
55
101
1000
1234321

输出样例

10
55
-1
715
94708

数据规模

对于 \(20%\) 数据， \(x \leq 10^6\)。

对于 \(100%\) 数据， \(n \leq 10, x \leq 10^{60}\)

题解

“为什么要攀登？因为山就在那里。”

非常板的数位 DP，在 DFS 时多记录一下之前是否下降过，如果下降过就不能再上升，其它跟普通数位 DP 一样。

完整代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 69;
int a[N], dp[N][10][2][2], T, len;
char ch[N];
int dfs(int pos, int pre, int down, int lim){
	if(pos == len + 1)
		return 1;
	if(dp[pos][pre][down][lim] != -1)
		return dp[pos][pre][down][lim];
	int up = lim ? a[pos] : 9, ans = 0;
	for(int i = 0; i <= up; i++){
		if(!down){
			if(i < pre)
				ans += dfs(pos + 1, i, 1, lim && i == up);
			else
				ans += dfs(pos + 1, i, 0, lim && i == up);
		} else if(i <= pre)
			ans += dfs(pos + 1, i, 1, lim && i == up);
	}
	return dp[pos][pre][down][lim] = ans;
}
signed main(){
	freopen("hill.in", "r", stdin);
	freopen("hill.out", "w", stdout);
	scanf("%lld", &T);
	while(T--){
		scanf("%s", ch);
		len = strlen(ch);
		for(int i = 0; i < len; i++)
			a[i + 1] = ch[i] - '0';
		bool flag = false, flag2 = false;
		for(int i = 2; i <= len; i++){
			if(a[i - 1] > a[i])
				flag = true;
			if(flag && a[i] > a[i - 1]){
				flag2 = true;
				break;
			}
		}	
		if(flag2)
			printf("-1\n");
		else {
			memset(dp, -1, sizeof(dp));
			printf("%lld\n", dfs(1, 0, 0, 1) - 1);
		}	
	}
	return 0;
}

T3

题目描述

有一个 \(4 \times N\) 的木板需要粉刷，第 \(i\) 行 \(j\) 列的颜色记为 \(A_{i, j}\)。有 \(256\) 种颜色，记为 \(0 \dots 255\)，为了使得粉刷比较好看，粉刷需要满足如下要求:

  1. \(A_{x, y} \geq A_{x, y - 1}\)。

  2. 有一些指定的 \((x_1, y_1)\) 和 \((x_2, y_2)\)，要求 \(A_{x_1, y_1} = A_{x_2, y_2}\)。

请问有多少种满足要求的粉刷方式？输出答案的最后 \(5\) 位即可。

输入格式

第一行两个数 \(n, m\)，表示木板的长度，和指定规则的条目个数。

接下来 \(m\) 行，每行四个数 \(x_1, y_1, x_2, y_1\)，此规则表示 \(A_{x_1, y_1}\) 需要等于 \(A_{x_2, y_2}\)。

输出格式

一个整数，表示答案的末 \(5\) 位。

输入样例1

1 0

输出样例1

67296

输入样例2

1 3
1 1 2 1
1 1 3 1
4 1 3 1

输出样例2

00256

提示

输出可以使用 %05d 输出。

数据规模

对于 \(30\%\) 数据，\(n ≤ 3, m = 0\)。

对于 \(100\%\) 数据，\(1 \leq n \leq 15, 0 \leq M \leq 100, x_1, x_2 \leq 4, y_1, y_2 \leq n\)。

T4

题目描述

有一个 \(N \times M\) 的棋盘，要在上面摆上 knight，每个格子可以放至多一个 knight。

knight 的攻击范围如下图：

所有 knight 不能互相攻击，请问总共有多少可行的摆法？答案对 \(1000000007\) 取模。

输入格式

第一行个数 \(t\)，表示测试的组数。

接下来 \(t\) 组，每组两个整数，\(n\) 和 \(m\)。

输出格式

一共 \(t\) 行，第 \(i\) 行表示第 \(i\) 组的答案。

输入样例

4
1 2
2 2
3 2
3 31415926

输出样例

4
16
36
933912086

数据规模

对于 \(70\%\) 数据，\(m \leq 100\)。

对于 \(100\%\) 数据，\(t \leq 10, n \leq 3, m \leq 10^9\)。

题解

由于 \(n\) 比较小，所以考虑状压的思想，有马的位置标记为 \(1\)，无马的位置标记为 \(0\)，将两列压成一个二进制数，由于马不能相互攻击，因此这样的状态有 \(36\) 种。

那么原问题就相当于是将 \(m - 1\) 个这样的两排 每两排重叠一排地拼在一起，马不能相互攻击，重叠的两排有相同的一排，有多少种方法可以拼出整个棋盘。

比如，下面的两个局面可以拼在一起：

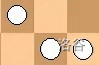
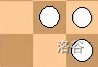
拼成：

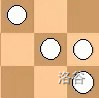
如果我们将有相同一排，且重叠一排拼在一起后马不能互相攻击的局面建立一条无向边，用邻接矩阵存图。

现在有一个重要结论：邻接矩阵的 \(n\) 次方中 \(A_{i, j}\) 表示 \(i\) 到 \(j\) 的不同路径中长度为 \(n\) 的路径条数 (我不会证qwq)

那么我们只用将这个邻接矩阵的 \(m - 1\) 次方算出来，将矩阵中第一排每个数加起来就是答案。

完整代码

#include <bits/stdc++.h>
using namespace std;
#define int long long 
const int P = 1000000007;
int n, cnt;
int rev[(36 + 1)];
struct Mat{
	int a[(36 + 1)][(36 + 1)];
	void Mat0(){
		for(int i = 1; i <= cnt; ++ i)
			for(int j = 1; j <= cnt; ++ j)
				a[i][j] = 0;
	}
	void Mat1(){
		for(int i = 1; i <= cnt; ++ i){
			for(int j = 1; j <= cnt; ++ j)
				a[i][j] = 0;
			a[i][i] = 1;
		}
	}
} x, ansmat;
Mat operator * (Mat &s, Mat &t){
	Mat res;
	res.Mat0();
	for(int i = 1; i <= cnt; ++ i)
		for(int j = 1; j <= cnt; ++ j)
			for(int k = 1; k <= cnt; ++ k)
				res.a[i][j] = (res.a[i][j] + s.a[i][k] * t.a[k][j] % P) % P;
	return res;
}
Mat Qpow(Mat s, int k){
	Mat res;
	res.Mat1();
	while(k){
		if(k & 1)
			res = s * res;
		s = s * s;
		k >>= 1;
	}
	return res;
}

int Check(int s){//判断局面是否合法
	if(n == 1)
		return 1;
	if(n == 2){
		if((s & 1) == 1 && ((s >> 5) & 1) == 1)
			return 0;
		if(((s >> 1) & 1) == 1 && ((s >> 4) & 1) == 1)
			return 0;
		return 1;
	}
	if((s & 1) == 1){
		if(((s >> 5) & 1) == 1)
			return 0;
		if(((s >> 7) & 1) == 1)
			return 0;
	}
	if(((s >> 1) & 1) == 1){
		if(((s >> 6) & 1) == 1)
			return 0;
		if(((s >> 8) & 1) == 1)
			return 0;
	}
	if(((s >> 2) & 1) == 1){
		if(((s >> 3) & 1) == 1)
			return 0;
		if(((s >> 7) & 1) == 1)
			return 0;
	}
	if(((s >> 3) & 1) == 1)
		if(((s >> 8) & 1) == 1)
			return 0;
	if(((s >> 5) & 1) == 1)
		if(((s >> 6) & 1) == 1)
			return 0;
	return 1;
}
signed main(){
	freopen("knight.in", "r", stdin);
	freopen("knight.out", "w", stdout);
	int t;
	scanf("%lld", & t);
	while(t --){
		int m;
		scanf("%lld%lld", &n, &m);
		cnt = 0;
		for(int s = 0; s < (1 << (n << 1)); s++){
			if(n == 3 && (((s & 1) == 1 && ((s >> 5) & 1) == 1) || (((s >> 2) & 1) == 1 && ((s >> 3) & 1) == 1)))
				continue;
			rev[++cnt] = s;
		}
		x.Mat0();
		for(int i = 1; i <= cnt; i++)
			for(int j = 1; j <= cnt; j++)
				if((rev[j] % (1 << n)) == (rev[i] >> n) && Check(rev[i] | ((rev[j] >> n) << (n << 1))) == 1)//判断两个局面是否能重叠一排拼在一起
					x.a[i][j] = 1;
		ansmat = Qpow(x, m);//矩阵快速幂，此处必须m次方
		int ans = 0;
		for(int j = 1; j <= cnt; j++)
			ans = (ans + ansmat.a[1][j]) % P;
		printf("%lld\n", ans);
	}
	return 0;
}

标签：输出,return,leq,2024.8,校测,30,样例,int,dp
From： https://www.cnblogs.com/JPGOJCZX/p/18422878

相关文章

  • 分块/莫队学习笔记（一）（2024.8.23）
    分块基本概念分块的基本思想是，通过对原数据的适当划分，并在划分后的每一个块上预处理部分信息，从而较一般的暴力算法取得更优的时间复杂度。分块的时间复杂度主要取决于分块的块长，一般可以通过均值不等式求出某个问题下的最优块长，以及相应的时间复杂度。LOJ小分块#6277.数列分......
  • 2024.8.31校测
    T1题目描述今天的酒席有\(n\)个人，他们要同时举杯，成对碰杯。碰杯的时候，不能有人不参与碰杯，也不希望有手臂交叉这种别扭的情况出现。如下图，左图的情况是好的，右图的情况是不希望出现的。每个人都有一个喜爱的酒种类，每个人想要与和自己喝一样酒的人碰杯，请你设计一个方法，在保证每......
  • 2024.9.6校测
    T1题目描述猫猫是丛林里很多动物心中的天使，她为此十分自豪。猫猫最爱吃鱼了，她每天都要去池塘钓鱼吃。猫猫经常吃鱼脑，数学特别强，然而，小女生的性格决定了她的贪玩。一天，猫猫钓到了很多条鱼。她并不想马上就把可怜的鱼儿吃掉，而是先折磨够之后再吃（有句话叫什么来着，最毒不过猫猫心）。......
  • 2024.9.16上午校测
    T1题目描述首先，让我们来一道萌萌哒的并查集吧。你有\(n\)个萌萌哒元素。每个元素都单独在一个集合中。同时，我们有\(n-1\)个操作，每次合并两个元素所在的集合，保证合并前两个元素位于不同的集合。现在有\(m\)个询问\((x,y)\)，每次询问需要你输出元素\(x,y\)第一次位......
  • 2024.9.13校测
    T1题目描述Gnaw刚刚学习在数字逻辑中学到了格雷码，它的定义是这样的，对于二进制数\(A\)，它对应的格雷码为\(G=A\operatorname{xor}(A>>1)\)，格雷码有个很有趣的性质是相邻二进制数对应的格雷码只有一位不同。现在以\(01?\)的方式给出一个长为的二进制数\(m\)，\(?\)表示......
  • 2024.9.16下午校测
    T1题目描述有\(n\)个人站成一行，每个人有一个魅力值，相同魅力值的人会形成一个团伙，你出于对于社会和谐发展的考虑，定义一个团伙正常当且仅当团伙人数为\(2\)，现在你的任务就是回答\(M\)个询问，每次询问一个区间\([L,R]\)，你需要回答这个区间中所有人各自结成团伙后，处于不正常团......
  • 图论进阶学习笔记（三）（2024.8.12）
    二分图定义如果你能把一个图划分成两个集合，集合内部的点没有边相连接，那么这个图就是一个二分图，如图就是一个二分图：交错路：从一个没有被匹配的点出发，依次走非匹配边，匹配边，非匹配边……最后到达另外一部点当中某个没有被匹配的点的路径。增广路：从一个没有被匹配的点出发，依次走......
  • 图论进阶学习笔记（二）（2024.8.1）
    图的连通性强连通分量割点缩点例题一边双连通分量点双连通分量2-SAT例题二例题三欧拉回路例题四......
  • GEE教程：对降水数据进行重投影（将10000m分辨率提高到30m）
    目录简介函数projection()Arguments:Returns: ProjectionnominalScale()Arguments:Returns: FloatsetDefaultProjection(crs, crsTransform, scale)Arguments:Returns: Image代码结果简介在GEE中进行重投影和重分类的步骤如下：1.选择目标图层。2.使用......
  • 线段树进阶应用学习笔记（一）（2024.7.19）（2024.8.22）
    线段树优化建图算法流程复杂度分析例题一#include<bits/stdc++.h>usingnamespacestd;#defineintlonglongconstintN=5e5,M=5e6+9;structEdge{ intv,w,nex;}e[M];inthead[M],ecnt;voidAddEdge(intu,intv,intw){ e[++ecnt]=Edge{v,w,hea......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99