T1
题目描述
今天的酒席有 \(n\) 个人,他们要同时举杯,成对碰杯。碰杯的时候,不能有人不参与碰杯,也不希望有手臂交叉这种别扭的情况出现。如下图,左图的情况是好的,右图的情况是不希望出现的。
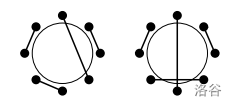
每个人都有一个喜爱的酒种类,每个人想要与和自己喝一样酒的人碰杯,请你设计一个方法,在保证每个人参与碰杯,且没有手臂交叉的情况下,有最多的人与喝一样酒的人碰杯,输出最多有多少人能与喝一样酒的人碰杯。
输入格式
第一行一个数 \(n\),表示酒桌上人的个数。
第二行 \(n\) 个数 \(c_i\),逆时针方向依次表示坐在第 \(i\) 个位置的人喝哪种酒,第 \(1\) 个和第 \(n\) 个人是相邻的。
输出格式
一个整数,表示在保证每个人参与碰杯,且没有手臂交叉的情况下,最多有多少人能与喝一样酒的人碰杯。
输入样例
6
1 2 2 3 3 1
输出样例
3
数据规模
对于 \(10 \%\) 的数据,\(2 \leq n \leq 10\)。
对于 \(100 \%\) 的数据,\(2 \leq n \leq 1000\),\(1 \leq c_i \leq 100\)。
题解
考虑区间 DP。
设 \(dp_{i, j}\) 表示第 \(i\) 到第 \(j\) 个人不交叉碰杯的最优解,首先可以发现 \(j - i + 1\) 必须为偶数,否则就会单一个人无法碰杯,因此只枚举长为偶数的区间即可,可以降低常数。
答案很简单,就是 \(dp_{1, n}\),考虑如何转移。
可以发现,如果出现下图这种情况:
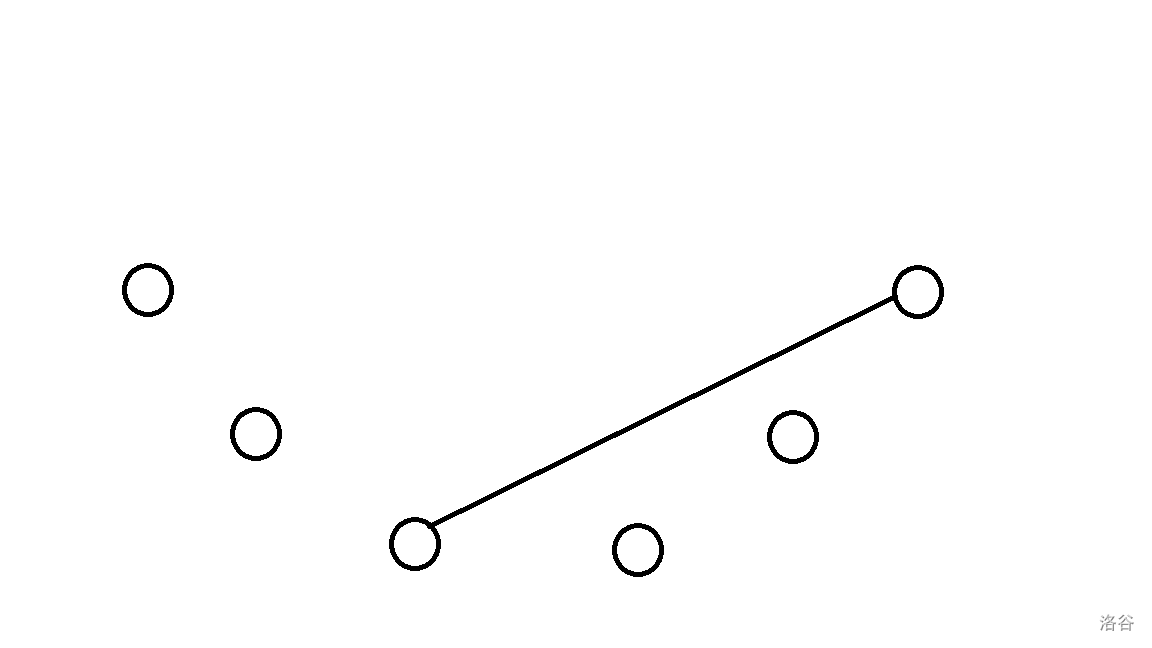
那么这条线左右两边的人都无法碰杯,这样就将大问题转化为了一模一样的小问题。于是,我们可以枚举这条分割线的两个端点,就可以得到以下 DP 转移方程:
\[dp_{i, j} = \begin{cases} \max_{i \leq k < j}dp_{i, k - 1} + dp_{k + 1, j - 1} & : a_k \neq a_j\\ \max_{i \leq k < j}dp_{i, k - 1} + dp_{k + 1, j - 1} + 1 & : a_k = a_j \end{cases} \]这样状态个数为 \(O(n^2)\),转移复杂度为 \(O(n)\),总复杂度 \(O(n^3)\),足以通过此题。
完整代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 9;
int a[N], dp[N][N], n;
bool flag;
int main(){
freopen("toasting.in", "r", stdin);
freopen("toasting.out", "w", stdout);
scanf("%d", &n);
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
for(int j = 2; j <= n; j++)
for(int i = j - 1; i >= 1; i -= 2)
for(int k = i; k < j; k += 2){
if(a[j] == a[k])
dp[i][j] = max(dp[i][j], dp[i][k - 1] + dp[k + 1][j - 1] + 1);
else
dp[i][j] = max(dp[i][j], dp[i][k - 1] + dp[k + 1][j - 1]);
}
printf("%d", dp[1][n]);
return 0;
}
T2
题目描述
院子里有一颗又高又大的草莓树,草莓树有 \(n\) 个节点,每个节点都结了一个草莓,吃掉第 \(i\) 个结点的草莓可以得到 \(a_i\) 的营养值,由于草莓可能会坏掉,所以 \(a_i\) 可能为负值,也可能为 \(0\)。现在要砍掉这颗树的两条边,使树变成三份,并且使得三份各自草莓营养值的和恰好一样。请问是否有这样的方法呢?如果有,请输出 YES,否则输出 NO。
输入格式
第一行一个数 \(t\),表示测试点的个数。
接下来 \(t\) 组:
每组第一行一个数 \(n\),表示结点的个数。
接下来 \(n\) 行,每行两个数 \(fa_i\) 和 \(a_i\),表示第 \(i\) 个结点的父亲是 \(fa_i\),第 \(i\) 个结点有营养值为 \(a_i\) 的草莓,根节点的 \(fa_1\) 记为 \(0\)。
输出格式
输出 \(t\) 行,如果第 \(t\) 组有解,则输出 YES,否则输出 NO
输入样例
2
6
2 4
0 5
4 2
2 1
1 1
4 2
6
2 4
0 6
4 2
2 1
1 1
4 2
输出样例
YES
NO
样例解释
第一组可以切掉 \(1\) 号和 \(4\) 号的父边,形成均等的三份。
数据规模
对于 \(10 \%\) 的数据,\(3 \leq n \leq 100\)。
对于 \(100 \%\) 的数据,\(t \leq 20\),\(3 \leq n \leq 100000\),\(-100 \leq a_i \leq 100\)。
题解
这里给出一种简单的 DFS 做法。
首先,如果这棵树上所有苹果的营养值之和不是 \(3\) 的倍数,那么一定无法将这棵树按照要求划分,直接输出 NO。
否则,就从根节点开始 DFS,同时记录以每个点为根的子树营养值的和,如果遇到一棵子树的营养值的和为总营养值的 \(\frac 13\),那么将答案加 \(1\),并将这棵子树的营养值和设为 \(0\) 来消除影响。如果最后统计到的答案大于 \(3\) (其实大于2就可以了),那么这颗树就可以划分成 \(3\) 个营养值相同的部分。
完整代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
struct Edge{
int v, nex;
} e[N << 1];
int head[N], ecnt;
void addEdge(int u, int v){
e[++ecnt] = Edge{v, head[u]};
head[u] = ecnt;
}
int T, fa[N], a[N], siz[N], n, rt, cnt, s;
void dfs(int u){
for(int i = head[u]; i; i = e[i].nex){
int v = e[i].v;
if(v == fa[u])
continue;
dfs(v);
siz[u] += siz[v];
}
if(siz[u] == s / 3){
cnt++;
siz[u] = 0;
}
}
void init(){
memset(siz, 0, sizeof(siz));
memset(head, 0, sizeof(head));
ecnt = 0;
cnt = s = 0;
}
int main(){
freopen("strawberry.in", "r", stdin);
freopen("strawberry.out", "w", stdout);
scanf("%d", &T);
while(T--){
init();
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d%d", &fa[i], &a[i]);
if(fa[i] != 0){
addEdge(i, fa[i]);
addEdge(fa[i], i);
} else
rt = i;
s += a[i];
}
for(int i = 1; i <= n; i++)
siz[i] = a[i];
if(s % 3 != 0)
printf("NO\n");
else {
dfs(rt);
if(cnt >= 2)
printf("YES\n");
else
printf("NO\n");
}
}
return 0;
}
T3
题目描述
有的词语常常别有深意,比如 \(\texttt{hehe}\) 可以单纯的表示 \(\texttt{hehe}\),也可以表示 \(\texttt{excuse me?!}\) ,现给出一段话 \(s\),和一个单词 \(t\),已知单词 \(t\) 有别有深意,也就是说有两个意思,求 \(s\) 可能有多少个意思?答案对 \(1000000007\) 取模。
输入格式
第一行一个数 \(n\),表示测试的组数。
接下来 \(n\) 组,每组两行,表示 \(s\) 和 \(t\)。
输出格式
一共 \(n\) 行,第 \(i\) 行表示第 \(i\) 组的 \(s\) 个意思个数。
输入样例
4
hehehe
hehe
woquxizaolehehe
woquxizaole
hehehehe
hehe
woyaoqugenbierenliaotianle
wanan
输出样例
3
2
5
1
样例解释
黑色表示取原意,红色表示取深意。
第 1 组: \(\texttt{\red{hehe}he}, \texttt{hehehe}, \texttt{he\red{hehe}}\)。
第 3 组: \(\texttt{hehehehe}, \texttt{hehe\red{hehe}}, \texttt{\red{hehe}hehe}, \texttt{he\red{hehe}he}, \texttt{\red{hehehehe}}\)。
数据规模
对于 \(50\%\) 数据,\(len(t) \leq len(s) \leq 1000\)。
对于 \(100\%\) 数据,\(len(t) \leq len(s) \leq 100000, n \leq 10\)。
\(s\) 和 \(t\) 仅包含小写字母。
题解
首先先用 KMP 找出模式串在文本串中的位置,设 \(dp_i\) 表示最后一个 取深意的位置 是文本串中第 \(i\) 个匹配 的不同深意个数,记匹配个数为 \(num\)。
那答案就是 \(\displaystyle\sum_{i=1}^{num}dp_i\),考虑如何转移
我们发现,当枚举到 \(i\) 个匹配时,只要在第 \(i\) 个匹配之前,且与第 \(i\) 个匹配没有交集的匹配的 \(dp\) 值都应加入到 \(dp_i\) 中,可以预处理这种匹配的个数 \(pre_i\),就可以写出 DP 转移方程:
\(dp_i = \displaystyle\sum_{j=1}^{pre_i}dp_j\)
发现转移是一段区间和,可以用树状数组或前缀和优化成 \(O(1)\)
注意,本题需要初始化 \(dp_1 = 1\)
这样,状态个数为 \(O(n)\),转移复杂度 (我用的是树状数组) 为 \(O(\log n)\),总复杂度为 \(O(n \log n)\),足以通过此题。
完整代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, MOD = 1000000007;
int nex[N], last[N], dp[N], cnt, T, lens, lenp;
char s[N], p[N];
int pre[N], t[N];
bool flag[N];
void init(){
memset(nex, 0, sizeof(nex));
memset(last, 0, sizeof(last));
memset(dp, 0, sizeof(dp));
memset(flag, 0, sizeof(flag));
memset(pre, 0, sizeof(pre));
memset(t, 0, sizeof(t));
cnt = 0;
}
void get(){
nex[0] = nex[1] = 0;
for(int i = 1; i < lenp; i++){
int j = nex[i];
while(j && p[i] != p[j])
j = nex[j];
if(p[i] == p[j])
nex[i + 1] = j + 1;
else
nex[i + 1] = 0;
}
}
void kmp(){
int j = 0;
for(int i = 0; i < lens; i++){
while(j && s[i] != p[j])
j = nex[j];
if(s[i] == p[j])
j++;
if(j == lenp)
last[++cnt] = i;
}
}
int lowbit(int x){
return x & -x;
}
void update(int x, int d){
while(x <= N){
t[x] += d;
x += lowbit(x);
}
}
int sum(int x){
int ans = 0;
while(x > 0){
ans += t[x];
ans %= MOD;
x -= lowbit(x);
}
return ans;
}
signed main(){
freopen("meaning.in", "r", stdin);
freopen("meaning.out", "w", stdout);
scanf("%lld", &T);
while(T--){
init();
scanf("%s", s);
scanf("%s", p);
lens = strlen(s);
lenp = strlen(p);
get();
kmp();
int ans = 1;
if(cnt == 0)
printf("%lld\n", ans);
else {
for(int i = 1; i <= cnt; i++)
flag[last[i]] = 1;
for(int i = 0; i < lens; i++){
pre[i] = pre[i - 1];
if(flag[i])
pre[i]++;
}
dp[1] = 1;
update(1, 1);
for(int i = 2; i <= cnt; i++){
int tmp = i - pre[last[i]] + pre[last[i] - lenp];
dp[i] = 1;
if(tmp > 0){
dp[i] += sum(tmp);
dp[i] %= MOD;
}
update(i, dp[i]);
}
for(int i = 1; i <= cnt; i++){
ans += dp[i];
ans %= MOD;
}
printf("%lld\n", ans);
}
}
return 0;
}
T4
题目描述
斐波那契序列是这样一个序列 \(A\),其中所有 \(A_i = A_{i - 2} + A_{i - 1}\)。现在给出一个序列 \(C\),求其中的最长斐波那契子序列。
输入格式
第一行一个数 \(n\),表示序列的长度。
第二行 \(n\) 个数,第 \(i\) 个数表示 \(C_i\)。
输出格式
一个整数,表示最长斐波那契子序列长度。
输入样例
10
1 1 3 -1 2 0 5 -1 -1 8
输出样例
5
数据规模
对于 \(10\%\) 数据,\(n \leq 100\)。
对于 \(100\%\) 数据,\(n \leq 3000, abs(C_i) \leq 10^9\)。
题解
考虑像求最长不下降子序列一样,设 \(dp_{j, i}\) 表示以 \(C_i\) 为子序列第一个数, \(C_j\) 为子序列第二个数的最长斐波那契子序列长度。
那么答案就是 \(\max_{1 \leq i \leq n, 1 \leq j < i}dp_{j, i}\)
考虑转移,如果能找到一个位置 \(k\) 使得 \(C_i + C_j = C_k\),那么 \(dp_{j, i}\) 就可以从 \(dp_{i, k}\) 转移到 \(dp_{j, i}\),就可以得到 DP 转移方程:
\(dp_{j, i} = \max(dp_{j, i}, \max_{C_i + C_j = C_k}dp_{i, k} + 1)\)
朴素枚举为 \(O(n^3)\) 的,如果我们将枚举到的所有 \(C_i\) 都插入到一个数据结构中,每次查询 \(C_i + C_j\),就可以将复杂度降至 \(O(n \log n)\),足以通过此题。
完整代码
#pragma GCC optimize(2)
#include <bits/stdc++.h>
using namespace std;
int read(){
int k = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')
f = -1;
c = getchar();
}
while(c >= '0' && c <= '9'){
k = k * 10 + c - '0';
c = getchar();
}
return k * f;
}
void write(int x){
if(x < 0){
putchar('-');
x = -x;
}
if(x < 10)
putchar(x + '0');
else {
write(x / 10);
putchar(x % 10 + '0');
}
}
const int N = 3e3 + 9;
int a[N], dp[N][N], n, ans;
unordered_map <int, short> mp;
int main(){
freopen("fibonacci.in", "r", stdin);
freopen("fibonacci.out", "w", stdout);
n = read();
for(register int i = 1; i <= n; i++)
a[i] = read();
if(n == 1)
write(1);
else {
for(register int i = 1; i <= n; i++)
for(register int j = i + 1; j <= n; j++)
dp[i][j] = 1;
ans = 0;
for(register int i = n; i >= 1; i--){
for(register int j = 1; j < i; j++){
int k = mp[a[i] + a[j]];
if(k != 0)
dp[j][i] = max(dp[i][k] + 1, dp[j][i]);
}
mp[a[i]] = i;
}
for(register int i = 1; i <= n; i++)
for(register int j = 1; j < i; j++)
ans = max(ans, dp[j][i]);
}
if(ans == 0)
write(2);
else
write(ans + 1);
return 0;
}