一定要看好乘的顺序!!!!!横的在前,竖的在后!
矩阵乘法和矩阵快速幂本身简单,但是构造出矩阵递推式的过程比较考验智慧。
1 矩阵乘法
1.定义
若矩阵A的大小为\(n \times m\),矩阵B的大小为\(m \times p\),则两个矩阵可以做乘法,得到的矩阵C的大小为\(n \times p\)。
\(A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix}\) \(B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32} \end{bmatrix}\) \(C = A \times B = \begin{bmatrix} a_{11}\times b_{11}+ a_{12} \times b_{21}+a_{13} \times b_{31} & a_{11} \times b_{12} + a_{12} \times b_{22} + a_{13} \times b_{32} \\ a_{21} \times b_{11} + a_{22} \times b_{21} + a_{23} \times b_{31} & a_{21} \times b_{12} + a_{22} \times b_{22} + a_{23} \times b_{32} \end{bmatrix}\)
注意:只有矩阵A的列数等于矩阵B的行数时,两个矩阵才能相乘。
2.代码实现
int a[N][N],b[N][N],c[N][N];
signed main()
{
#ifdef LOCAL
freopen("in.in","r",stdin);
#endif
int n = read(),m = read();
for(int i{1};i<=n;i++)
for(int j{1};j<=m;j++) a[i][j] = read();
int k = read();
for(int i{1};i<=m;i++)
for(int j{1};j<=k;j++) b[i][j] = read();
for(int i{1};i<=n;i++)
for(int j{1};j<=m;j++)
for(int l{1};l<=k;l++)
c[i][l] += a[i][j] * b[j][l];
for(int i{1};i<=n;i++)
{
for(int j{1};j<=k;j++)
writek(c[i][j]);
putchar(10);
}
exit(0);
}
2 矩阵快速幂
模版
注意在给 res 的初值赋成单位矩阵 \(I = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}\)。
const int N = 1e2+5;
int n;
const int MOD = 1e9+7;
struct MATRIX
{
int a[N][N]{};
void build(){for(int i{1};i<=n;i++) a[i][i] = 1;}
MATRIX operator *(const MATRIX md)
{
MATRIX as;
for(int i{1};i<=n;i++)
for(int j{1};j<=n;j++)
for(int k{1};k<=n;k++)
(as.a[i][k] += a[i][j] * md.a[j][k] % MOD ) %= MOD;
return as;
}
}mt;
inline MATRIX qp(MATRIX a,int b)
{
MATRIX ans;
ans.build();
while(b)
{
if(b&1) ans = ans * a;
a = a * a;
b>>=1;
}
return ans;
}
signed main()
{
#ifdef LOCAL
freopen("in.in","r",stdin);
#endif
n = read();
int k = read();
for(int i{1};i<=n;i++)
for(int j{1};j<=n;j++) mt.a[i][j] = read();
MATRIX ans = qp(mt,k);
for(int i{1};i<=n;i++)
{
for(int j{1};j<=n;j++) writek(ans.a[i][j]);
putchar(10);
}
Fibonacci第n项
题目描述:计算斐波那契数列第n项的后m位。
解析:
斐波那契数列的递推方程试可以写成矩阵的形式:
\(\begin{bmatrix} f[n] \\ f[n-1] \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} f[n-1] \\ f[n-2] \end{bmatrix}\)
那么:
\(\begin{bmatrix} f[n] \\ f[n-1] \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \times \begin{bmatrix} f[n-1] \\ f[n-2] \end{bmatrix} = \begin{bmatrix} 1&1\\1&0 \end{bmatrix} \times \begin{bmatrix} 1&1\\1&0 \end{bmatrix} \times \begin{bmatrix} f[n-2]\\f[n-3] \end{bmatrix} = \begin{bmatrix} 1&1\\1&0 \end{bmatrix}^{n-1} \times \begin{bmatrix} f[1]\\f[0] \end{bmatrix}\)
于是,我们只需要类比普通的快速幂计算矩阵
\(\begin{bmatrix} 1&1\\1&0 \end{bmatrix}\)
的快速幂即可。
Fibonacci前n项和
题目描述:
求\(d_n\)的前n项和\(S_n \bmod m\)。
解析:
考虑递推关系式:\(s[n] = s[n-1]+f[n]\),写成矩阵形式:
\(\begin{bmatrix} s[n]\\f[n+1]\\f[n] \end{bmatrix} = \begin{bmatrix} 1&1&0\\0&1&1\\0&1&0 \end{bmatrix} \times \begin{bmatrix} s[n-1]\\f[n]\\f[n-1] \end{bmatrix}\)
所以:
\(\begin{bmatrix} s[n]\\f[n+1]\\f[n] \end{bmatrix} = \begin{bmatrix} 1&1&0\\0&1&1\\0&1&0 \end{bmatrix}^{n-1} \times \begin{bmatrix} s[1]\\f[2]\\f[1] \end{bmatrix}\)
佳佳的Fibonacci
题目描述:
\(T(n) = f_1+2f_2+3f_3+\cdots+nf_n\),求\(T(n) \bmod m\)。
解析:
递推关系式的矩阵中不能出现变量n,所以要先对递推关系式变形成我们可以处理的情况。
\(\begin{aligned} T_n &= f_1+2f_2+3f_3+\cdots+nf_n \\ &= n \times S_n - S_{n-1} - S_{n-2} - S_{n-3} - \cdots - S_1 \\ &= n \times S_n - \sum _ {i=1}^{n-1} S_i \end{aligned}\)
而
\(\begin{aligned} \sum_{i=1}^{n-1} S_i &= S_1+S_2+S_3+\cdots+S_{n-1} \\ &= f_1+(f_1+f_2)+\cdots+(f_1+f_2+f_3+\cdots+f_{n-1}) \\ &= (n-1)f_1+(n-2)f_2+(n-3)f_3+\cdots+f_n \end{aligned}\)
令\(P_n = \sum_{i=1}^{n-1}S_i\),则: \(T_n=n\times S_n-P_n\)
我们不需要递推\(T_n\),只需要递推\(P_n\)和\(S_n\),再直接计算得到\(T_n\)。
因为\(P_n=P_{n-1}+S_{n-1}\),所以:
\(\begin{bmatrix} P_n\\S_n\\f_{n+1}\\f_n \end{bmatrix} = \begin{bmatrix} 1&1&0&0\\0&1&1&0\\0&0&1&1\\0&0&1&0 \end{bmatrix} \times \begin{bmatrix} P_{n-1}\\S_{n-1}\\f_n\\f_{n-1} \end{bmatrix}\)
[UVA10870] Recurrences
考虑矩阵加速递推。
令 \(F_{n}=\begin{bmatrix} f_{n} & f_{n+1} & f_{n+2} & \dots & f_{n+d-1} \end{bmatrix}\),容易有 \(\begin{aligned} F_{n} &=\begin{bmatrix} f_{n} & f_{n+1} & f_{n+2} & \dots & f_{n+d-1} \end{bmatrix} \\ &=\begin{bmatrix} f_{n-1} & f_{n} & f_{n+1} & \dots & f_{n+d-2} \end{bmatrix} \times \begin{bmatrix} 0 & 0 & 0 & \dots & a_{d} \\ 1 & 0 & 0 & \dots & a_{d-1} \\ 0 & 1 & 0 & \dots & a_{d-2} \\ \dots & \dots & \dots & \dots & \dots & \\ 0 & 0 & 0 & \dots & a_{1} \end{bmatrix} \\ &=\begin{bmatrix} f_{n-2} & f_{n-1} & f_{n} & \dots & f_{n+d-3} \end{bmatrix} \times \begin{bmatrix} 0 & 0 & 0 & \dots & a_{d} \\ 1 & 0 & 0 & \dots & a_{d-1} \\ 0 & 1 & 0 & \dots & a_{d-2} \\ \dots & \dots & \dots & \dots & \dots & \\ 0 & 0 & 0 & \dots & a_{1} \end{bmatrix}^{2} \\ &= \dots \\ &=\begin{bmatrix} f_{1} & f_{2} & f_{3} & \dots & f_{d} \end{bmatrix} \times \begin{bmatrix} 0 & 0 & 0 & \dots & a_{d} \\ 1 & 0 & 0 & \dots & a_{d-1} \\ 0 & 1 & 0 & \dots & a_{d-2} \\ \dots & \dots & \dots & \dots & \dots & \\ 0 & 0 & 0 & \dots & a_{1} \end{bmatrix}^{n-1} \\ &=F_{1} \times \begin{bmatrix} 0 & 0 & 0 & \dots & a_{d} \\ 1 & 0 & 0 & \dots & a_{d-1} \\ 0 & 1 & 0 & \dots & a_{d-2} \\ \dots & \dots & \dots & \dots & \dots & \\ 0 & 0 & 0 & \dots & a_{1} \end{bmatrix}^{n-1} \end{aligned}\)。
接着矩阵快速幂处理即可。
int MOD;
int d,n,m;
const int N = 20;
int b[N],f[N];
struct MATRIX
{
int a[N][N]{};
void build()
{
for(int i{1};i<=d+1;i++) a[i][i] = 1;
}
void build2()
{
for(int i{1};i<=d+1;i++)
a[1][i] = f[d+2-i];
}
void build3()
{
for(int i{1};i<=d;i++)
a[i][1] = b[i];
for(int i{2};i<=d+1;i++)
a[i-1][i] = 1;
}
void print()
{
for(int i{1};i<=d+1;i++)
{
for(int j{1};j<=d+1;j++) writek(a[i][j]);
putchar(10);
}
}
MATRIX operator *(const MATRIX md)
{
MATRIX as;
for(int i{1};i<=d+1;i++)
for(int j{1};j<=d+1;j++)
for(int k{1};k<=d+1;k++)
(as.a[i][j] += a[i][k] * md.a[k][j] % MOD) %= MOD;
return as;
}
};
inline MATRIX qp(MATRIX aa,int b)
{
MATRIX ans;
ans.build();
while(b)
{
if(b&1) ans = ans * aa;
aa = aa * aa;
b>>=1;
}
return ans;
}
signed main()
{
#ifdef LOCAL
freopen("in.in","r",stdin);
#endif
while(true)
{
d = read(),n = read(),MOD = read();
for(int i{1};i<=d;i++) b[i] = read();
for(int i{1};i<=d;i++) f[i] = read();
if(!d && !n && !MOD) break;
if(n<=d) {writeln(f[n]);continue;}
f[d+1] = 0;
for(int i{1};i<=d;i++)(f[d+1] += b[i]*f[d-i+1]) %= MOD;
MATRIX ori;
ori.build2();
MATRIX mt;
mt.build3();
mt = qp(mt,n-d-1);
ori = ori * mt;
writeln(ori.a[1][1]);
}
exit(0);
}
递推中存在常数的处理
1.\(f(n) = a \times f(n - 1) + b \times f(n - 2) + c\)
\(\begin{bmatrix} f_n\\f_{n-1}\\c \end{bmatrix} = \begin{bmatrix} a&b&1\\1&0&0\\0&0&1 \end{bmatrix} \times \begin{bmatrix} f_{n-1}\\f_{n-2}\\c \end{bmatrix}\)
2.\(f(n) = c^n - f(n - 1)\)
\(\begin{bmatrix} f_n\\c^n \end{bmatrix} = \begin{bmatrix} -1&c\\0&c \end{bmatrix} \times \begin{bmatrix} f_{n-1}\\c^{n-1} \end{bmatrix}\)
矩阵幂求和
题目描述:
给定一个矩阵,求\(S = A + A^2 + A^3 + \cdots + A^k\),求S中的每个数对P取模的结果。
解析:
法一:递归
对式子进行变形,比如:\(A + A^1 + A^2 + A^3 + A^4 + A^5 + A^6\)可以变形为\(A+A^1+A^2+A^3+A^3 \times (A+A^2+A^3) = (A^3+1)(A+A^2+A^3)\),所以这个式子可以递归。如果k为偶数直接递归即可;如果k为奇数,递归计算\(A^{k-1}\),之后单独计算\(A^k\)。
法二:分块矩阵
我们尝试使用
\(\begin{bmatrix} S_k\\A^k \end{bmatrix}\)
和
\(\begin{bmatrix} S_{k-1}\\A^{k-1} \end{bmatrix}\)
建立关系:
\(\begin{bmatrix} S_k\\S^k \end{bmatrix} = \begin{bmatrix} 1&A\\0&A \end{bmatrix} \times \begin{bmatrix} S_{k-1}\\A^{k-1} \end{bmatrix}\)
我们会发现,这里面是矩阵包含着矩阵,所以这个矩阵的长度为 \(A\)的长度乘 \(2\),同时下面的 \(1\)也为单位矩阵,\(0\) 也是一个矩阵,长度都为 \(A\) 的长度。我们求新矩阵的 \(n-1\)次方,就可以得到\(S_k\)。
图上路径方案
题目描述:
给定一个有向图的邻接矩阵 \(S\),问从点 \(a\) 恰好走 \(K\) 步(允许重复经过边)到达 \(b\) 点的方案数模$10007 $ 的值。
解析:
如下图: 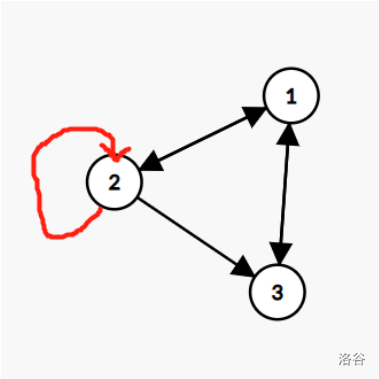
在图的邻接矩阵中,两点之间有连边用1表示,没有用0表示。
\(\begin{bmatrix} 0&1&1\\1&1&1\\1&0&0 \end{bmatrix}\)
换个角度来想,在邻接矩阵A中,\(a_{ij}\)正好表示从点i到点j走一步的方案数,我们尝试将矩阵乘起来,变成\(A^2\)。 在\(A^2\)中,\(A_{11}^2 = a_{11} \times a_{11} + a_{12} \times a_{21} + a_{13} \times a_{31}\)。在这个式子中,\(a_{ik}\)和\(a_{kj}\)都为1,才能对最终的答案贡献1,所以\(A_{ij}^s = A_{ik}^{s-1} + a_{kj}\)表示i到j走s步,可以是i到k走s-1步的基础上再走kj这条边,也就是多走了1步,所以乘一次邻接矩阵,相当于多走一步。所以本题我们直接对邻接矩阵做一个 \(k\) 的快速幂即可。
[USACO07NOV] Cow Relays G
题目描述:
给定一张T条边的无向连通图,求S到E经过M条边的最短路。
解析:
我们可以通过动态规划来解决此题。令\(f[i][j]\)表示达到i经过j条边的最短距离,那么转移方程如下:
\(f[i][j] = min(f[k][j - 1] + G[k][i])(1 <= k <= N)\)
其中N为总的点数,如果k和i之间有边相连,则\(G[k][i]\)为边权,否则为正无穷。
上述dp方程时间复杂度为\(O(N^2M)\),显然会T。 回顾矩阵乘法在图论里的应用式子:
\(C[i][j] = \sum_{k=1}^p A[i][k] \times B[k][j]\)
由于矩阵乘法满足分配律和结合律(不满足交换律),所以我们可以通过矩阵快速幂的方法来加速。于是:
\(C[i][j] = min(A[i][k] + B[k][j])(1<=k<=p)\)
例题7:[POJ 3734]Blocks
题目描述:
有 \(n\)个 blocks,让你用红,蓝,绿,黄四种颜色染上色,求红色和绿色的 block 都是偶数个的方案有多少个。
解析:
首先,令
\(dp[i][0]\) 表示当涂了前 \(i\) 个 blocks 之后,红色和绿色都是偶数个的方案数。
\(dp[i][1]\) 表示当涂了前 \(i\) 个 blocks 之后,红色和绿色只有一个是偶数个的方案个数。
\(dp[i][2]\) 表示当涂了前 \(i\) 个blocks之后,红色和绿色都不是偶数个的方案个数。
得出状态转移方程:
\(dp[i + 1][0] = 2 \times dp[i][0] + dp[i][1]\)
\(dp[i + 1][1] = 2 \times dp[i][0] + 2 \times dp[i][1] + 2 \times dp[i][2]\)
\(dp[i + 1][2] = dp[i][1] + 2 \times dp[i][2]\)
由于n<=1e9所以\(O(n)\)的dp是不行的,需要矩阵快速幂优化。
\(\begin{bmatrix} A(n)\\B(n)\\C(n) \end{bmatrix} = \begin{bmatrix} 2&1&0\\2&2&2\\0&1&2 \end{bmatrix} \times \begin{bmatrix} A(n-1)\\B(n-1)\\C(n-1) \end{bmatrix} \rightarrow \begin{bmatrix} A(n)\\B(n)\\C(n) \end{bmatrix} = \begin{bmatrix} 2&1&0\\2&2&2\\0&1&2 \end{bmatrix}^n \times \begin{bmatrix} A(0)\\B(0)\\C(0) \end{bmatrix}\)
[SCOI 2009] 迷路
题目描述:
该有向图有n个结点,从1到n编号。Windy从1出发,必须恰好在t时刻到达n。求有多少种不同的路径,答案对2009取模。
解析:
首先,如果题目中的每一条边只用0和1表示并且用邻接矩阵A来存这张图,那么在矩阵\(A^t\)中,\(A_{ij}^t\)表示由i到j经过t条边的情况总数。 但这道题这么做显然不行,因为我们所有的推论都建立在边权为1的情况上。
虽然我们不能直接使用我们的结论,但最大边权是9,n也不超过10,不算大。所以我们可以采用拆点:把一个点拆成多个点。
先来拆一个边权不超过2的图: 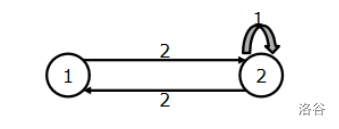
可得矩阵:
\(\begin{bmatrix} 0&2\\2&1 \end{bmatrix}\)
将其拆点: 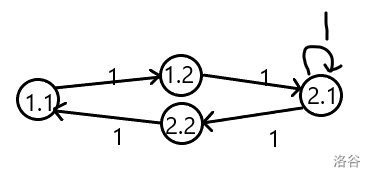
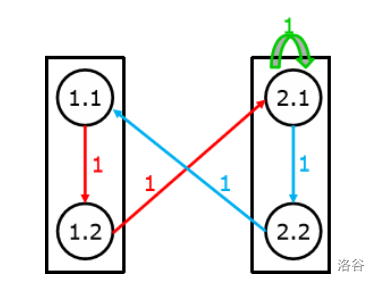
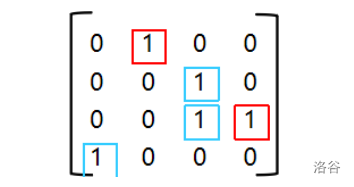
将1.1看成结点1;1.2看成结点2;2.1看成结点3;2.2看成结点4,可得新矩阵:
\(\begin{bmatrix} 0&1&0&0\\0&0&1&0\\0&0&1&1\\1&0&0&0 \end{bmatrix}\)
将其平方:
\(\begin{bmatrix} 0&0&1&0\\0&0&1&1\\1&0&1&1\\0&1&0&0 \end{bmatrix}\)
我们再对非零点进行分类,原先就有的1看成蓝色,后面通过自连得到的1看成红色: