图的连通性小记

标签：连通连通性 int 割点割边 dfn low 小记

前言

DFS 树

无向图 DFS 树

定义：DFS树是在图或树结构上进行深度优先搜索时形成的树。在 DFS 过程中，从一个顶点开始，尽可能深地搜索图的分支，直到达到一个没有未访问邻居的顶点，然后回溯到上一个顶点继续搜索。

从点 \(r\) 开始搜索，每次进入一个点 \(i\) 对应的边 \((fa_i,i)\) 为树边，其他的为回边。

图来源标于参考资料中。

有向图 DFS 树

对于若连通图，从一个点搜索不一定能搜到所有节点，一般是以森林的形式。

选择一个未访问的点，按无向图的方式建树，直到无法搜索。

每一棵子树如下图：

图片来源

一些同无向图不一样的边：

从祖先指向后代的非树边，称为 前向边。
从后代指向祖先的非树边，称为 返祖边（后向边）。
两端无祖先后代关系的非树边，称为 横叉边。

性质

在生成树种，图的回边连接的都是一个顶点和它的子孙节点。
当且仅当树边 \((u,v)\) 不存在连接其祖先和子孙节点的回边时，它是割边（桥）。

无向图连通性

割点与割边

定义

割点：在无向图中，删去后使得连通分量数增加的点称为割点。
割边：在无向图中，删去后使连通分量数增加的边称为割边，也称为桥。
将某种类型的连通分量根据等价性或独立性缩成一个点的操作称为缩点，原来连接两个不同连通分量的边在缩点后的图上连接对应连通分量缩点后形成的两个点。
必经点的定义：在从点 \(u\) 到点 \(v\) 的所有路径中，所有路径都必须经过的点。
两点边双连通是指它们在同一个边双内。两点点双连通是指它们在同一个点双内。

性质

边双的性质：

两点之间任意一条迹上的所有割边，就是两点之间的所有必经边。
边双和点双缩点后均得到一棵树，而强连通分量缩点后得到一张有向无环图。
如果在原图上新连一条边，设为：\((u,v)\)，那 \(u,v\) 所在边双的树上简单路径会被缩成一个大边双，所以边双具有传递性，即：若 \(a,b\) 双连通，\(b,c\) 双连通，那么 \(a,c\) 双连通。
两个点 \(u,v\) 双连通，当且仅当 \(u,v\) 之间没有必经边（割边）。
一条边双中的边 \((u,v)\)，删去后 \(u,v\) 依然联通，将此路径与边 \((u,v)\) 相接得到不经过重复边的回路，所以对于边双内任意一条边 \((u,v)\)，存在经过 \((u,v)\) 的回路。

推论：

对于边双内任意一条边 \((u,v)\)，存在不经过重复边的回路。
对于边双内任意一个点 \(u\)，存在经过 \(u\) 的回路。

点双的性质：

删去割点后不连通的两个点之间任意一条路径必然经过该割点，这割点为必经点。两点之间的所有割点 不一定是 两点之间的必经点，因为割点的定义是关于图的整体结构的，而必经点是针对具体的两点之间的所有路径。如果一个割点不位于两点之间的所有路径上，它就不是这两点之间的必经点。
点双两两可能有交，所以点双不具有传递性。
若两点双有交，那么交点一定是割点。因为如果点双有交，这个焦点一定阻碍了点双的扩大：删去此点依然联通，点双会扩大。
点双的交点是割点，但割点不一定是点双的交点，是一个点属于超过一个点双。
一条边恰属于一个点双。

可以得出定义：可知割点是连接点双的桥梁，正如割边是连接边双的桥梁。用一个点代表一个点双，并将点双代表点向它包含的割点连边，得到块割树（Block-Cut Tree，“点双连通块 - 割点” 树）。

对于一个 \(n>3\) 的点双，其中的点 \(u\) 存在经过 \(u\) 的简单环。

menger 定理

边形式：对于有限图中的任意两个不同顶点 \(u\) 和 \(v\)，它们之间的最大相互不相交路径的数量等于为了使 \(u\) 与 \(v\) 断开连接而必须删除的最小顶点数。
点形式：对于无向图上任意不同且不相邻的两点 \(u,v\)，使得 \(u,v\) 不连通所需删去的点的数量的最小值，等于 \(u,v\) 之间点不相交（不在除了 \(u,v\) 以外的点相交）的路径数量的最大值。

求割点

这里把 alex_wei 的话简单的复述一遍。

先构建出图的 DFS 树。

现在探究点 \(x\) 是否为割点，设 \(T(x)\) 为根为 \(x\) 的树，\(T'(x)\) 为图除去 \(T(x)\) 的部分，\(y\in T(x)\)。如果除去 \(x\)，\(y\) 与 \(T'(x)\) 中的节点都不相连，那么 \(x\) 就是割点。

所以现在问题变为：不经过 \(x\) 能到达的所有点都属于 \(T(x)\)。

设以点 \(y\) 为根的子树为 \(T(y)\)，点 \(u \in T(y)\)，点 \(v \in T'(x)\)。设存在一条路径使得 \(y\) 不经过 \(x\) 到达 \(T'(x)\)。\((u,v)\) 为跨越 \(T(y)\) 与 \(T'(x)\) 的一条边，可以知道 \(v\) 一定是 \(x,u\) 的祖先。

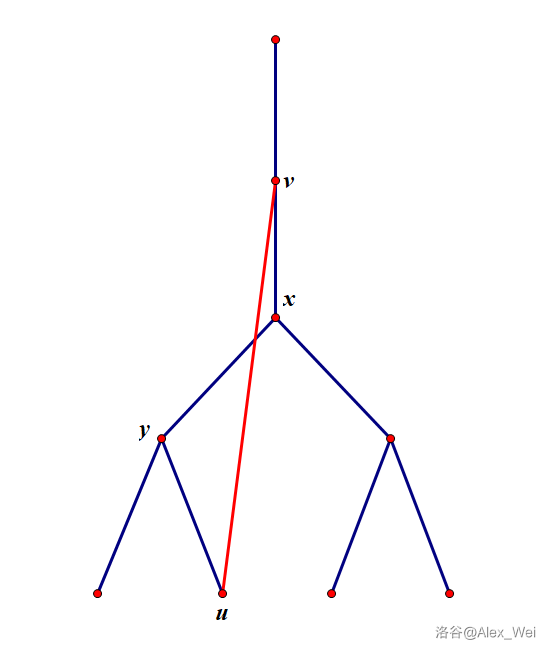
图来源标于参考资料中

可以知道不管是 \(y,u\) 一定都在除 \(x\) 的 \(x\) 为根的树内，所以割点的判断条件为除 \(x\) 的以 \(x\) 为根的子树内存在一个点 \(u\)，连接到 \(x\) 的祖先。

设 \(f_x\) 表示 \(x\) 通过非树边（回边）相连的点的 \(dfn\) 的最小值。

所以定义了 \(low_x\) 函数，表示 \(T(x)\) 中 \(f_x\) 的最小值。

所以非根结点的割点判定法则：

\(x\) 为割点当且仅当存在 \(u\) 属于除 \(x\) 的以 \(x\) 为子树中，且 \(low_u \le dfn_x\) 即不存在 \(x\) 的祖先与 \(u\) 相连。

如果是根节点，如果根节点的儿子数大于一，即 \(son_x \ge 2\)，可以把树分为几个联通块，所以是割点。

模板题 code:

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
vector<int>e[N];
int n,m;
int dfn[N],low[N],buc[N],tim;
void tarjan(int u,int fa)
{
    dfn[u]=low[u]=++tim;
    int son=0;
    for(auto v : e[u])
    {
        if(v==fa)   continue;
        if(!dfn[v])
        {
            son++,tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]&&fa!=0)   buc[u]=1;
        }
        else low[u]=min(low[u],dfn[v]);
    }
    if(son>=2&&fa==0)   buc[u]=1;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        e[u].push_back(v),e[v].push_back(u);
    }
    for(int i=1;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i,0);
    }
    int ans=0;
    for(int i=1;i<=n;i++)   ans+=buc[i];
    printf("%d\n",ans);
    for(int i=1;i<=n;i++)
        if(buc[i])  printf("%d ",i);
    return 0;
}

求割边

与割点差不多。

可以知道割边一定是树边，回边一定不是割边。

设一条边为 \((u,v)\)，\(u\) 是 \(v\) 的祖先，这条边为割边当且仅当 \(low_u<dfn[v]\)。

注意判树边的方法，一般图论题都会用 if(fa==v) continue;，但如果树边是重边就不好判断了。

如果用链式前向星，把 cnt=1 每条边的编号为 \(k,k+1\)，把当前编号异或一得到反边，如果用 vector 存图，开个 pair 存一下边的编号就可以了。

缩点只用开个栈，每次找到一个割边 \((u,v)\) 就从 \(u\) 一直出栈，直到 \(v\)，这样一个边双就缩成一个点。其他的缩点方式类似。

模板题 code:

#include<bits/stdc++.h>
#define pii pair<int,int>
using namespace std;
const int N=1e6+10;
int n,m;
vector<pii>e[N];
int tim,dfn[N],stk[N],top,low[N],tot;
vector<int>ans[N];
void form(int u)
{
    ++tot;
    do{ans[tot].push_back(stk[top]);}
    while(stk[top--]!=u);
}
void tarjan(int u,int fa)
{
    dfn[u]=low[u]=++tim;
    stk[++top]=u;
    for(auto t : e[u])
    {
        if(t.second==fa)    continue;
        int v=t.first;
        if(!dfn[v])
        {
            tarjan(v,t.second);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<low[v])   form(v);
        }
        else low[u]=min(low[u],dfn[v]);
    }   
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        e[u].push_back({v,i}),e[v].push_back({u,i});
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i]) tarjan(i,0),form(i);
    printf("%d\n",tot);
    for(int i=1;i<=tot;i++)
    {
        printf("%d ",ans[i].size());
        for(auto v : ans[i])    printf("%d ",v);
        puts("");
    }
    return 0;
}

有向图联通性

定义

强连通：对于有向图上两点 \(u,v\) 如果两点可以互相到达，称两点强连通。

强连通图：满足任意两点强连通的有向图称为强连通图。它等价于图上任意点可达其它所有点。

强连通分量：有向图的极大强连通子图称为强连通分量（Strongly Connected Component，SCC）。

性质

前文可知，无向图的 DFS 树还有返祖边、横叉边与前向边。如果用时间戳记录搜索顺序，返祖边与横叉边是指向时间戳比他早的节点，而前向边不是，根据上文无向图的经验，应该探讨返祖边与横叉边。

若 \(u,v\) 强连通，\(u,v\) 树上路径上的所有点都强连通。
设 \(f_x\) 为 \(x\) 的所有 \(x\) 的返祖边、横叉边 \((u,v)\)，\(u\) 的最小时间戳，\(x\) 是关键点（某个 scc 的最浅节点），当且仅当 \(f_x \ge dfn_x\)。

tarjan 求 scc

\(f_x\) 的定义与上文的无向图大致相同，得到关键点的方法与求割点大致相同，所以考虑如何求 scc。

为了找到最浅节点，也就是使强连通子图最大，选取的关键点是：\(f_x=dfn_x\)。

要得到这个子图，用栈维护，搜到一个点就加入栈，找到关键点就回退栈。

模板 code:

缩完点之后的图是 DAG，点的编号的逆序满足拓扑序。

再探 DFS 树

树上差分求割边

结论：当且仅当树边 \((u,v)\) 不存在连接其祖先和子孙节点的回边时，它是割边。也就是说，树边 \((u,v)\) 是桥当且仅当此时没有回边跨越它。

所以求割点的方法为：

建立这张图的 DFS 树。
对每一条树边 \((u,v)\)，寻找是否有一条回边跨越 \((u,v)\)，如果没有，它就是割边。

对于第二条，可以再建树时判断哪些时回边，并知道祖孙关系，然后标记两点，做个差分即可。

无向图加方向转为强连通图

先判断能否转为强连通图：如果图中有割边，则一定无法构成。

现在图是一个大的边双，又知道边双中任意一点都存在回路，所以只用在割点判断时记录路径即可。

后言

参考资料：

alex_wei：图论1。
DFS 树

标签：连通,连通性,int,割点,割边,dfn,low,小记
From： https://www.cnblogs.com/hutongzhou/p/18409018

前言