解决的问题
有 \(n\) 个值,每个值有两个信息 \((a_i, b_i)\)。你需要在这 \(n\) 个值间连边并形成一棵二叉树,使得:
- 每个点的 \(a_i\) 满足二叉搜索树的性质。即对于所有 \(v \in \text{subtree}_{lson}\) 都有 \(a_v \le a_u\),对于所有 \(v \in \text{subtree}_{rson}\) 都有 \(a_v > a_u\)。
- 每个点的 \(b_i\) 满足小根堆的性质。即对于所有 \(v \in \text{subtree}_u\) 都有 \(a_v \ge a_u\)。
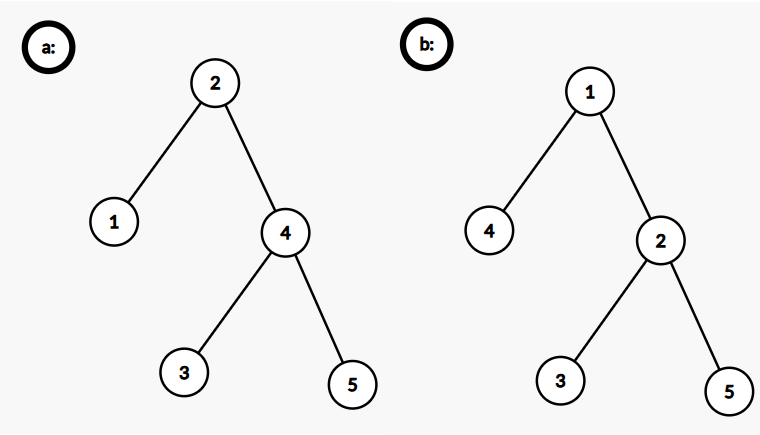
例如当 \(a = \{1,2,3,4,5\},b = \{4, 1, 3, 2, 5\}\) 时
算法
首先我们将所有值按照 \(a\) 升序排序。然后从左往右向树中插入。显然当一个值被插入时它的 \(a\) 一定是最大的。
此时我们默认插入新值之前的二叉树是合法的。
我们回忆一颗二叉搜索树中的最大值是什么。因为一个点的右儿子的权值一定比自己大,所以我们从根开始不断往右走,走不动时所在的点就是二叉搜索树中的最大值。例如在上左图中最大值 \(5\) 就是从根一直走右儿子得到的。
我们定义从根开始,如果一直可以就走到当前点的右儿子,这个过程中经过点构成的序列为右链。例如上左图中右链为 \(2,4,5\)。那么二叉搜索树上的最大值就是这棵树的右链的最后一个元素。
回到原问题。我们希望在新值的 \(a\) 最大,也就是成为树上右链的末端。
但是直接将其设为当前右链末端的右儿子肯定不行。因为这可能导致小根堆的条件不满足。我们考虑调整颗树的形态。
具体的,因为插入新值之前这棵树的形态是正确的,所以右链上的点的 \(b\) 权值一定随深度递增(小根堆)。例如上右图中的 \(1,2,5\)。所以将新值插入后右链上 \(b\) 的单调性必须仍保持。
所以如果我们要插入值 \((6, 4)\):
- 右树中 \(4\) 的位置必须要在 \(2,5\) 之间。这样能保证 \(b\) 的小根堆性质。
- 左树中 \(6\) 的位置必须在右链末端。这样能保证 \(a\) 的二叉搜索树性质。
最好的调整方法是这样:
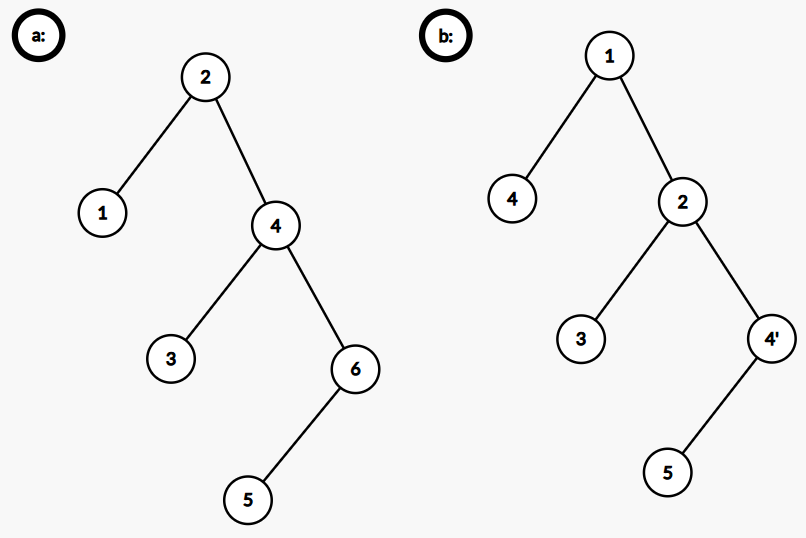
即 \(rson((4,2)) \gets (6,4)\),\(lson((6,4)) \gets (5,5)\)。其余点的左右儿子均不改动。
实现上,我们维护一个栈存储当前树上的右链。栈顶元素为右链末端,栈底元素为根。每次插入一个值 \((a_i,b_i)\) 时,我们找到当前栈内最靠上的一个点 \(j\) 满足 \(b_j > b_i\),并将 \(j\) 及以上的点全部弹栈。令 \(k\) 表示操作后的新栈顶,然后执行 \(rson(k) \gets i,lson(i) \gets j\) 即可。
建出来的树即笛卡尔树。
P5854 【模板】笛卡尔树 的代码如下。因为这道题的二叉搜索树权值就是下标,所以不用排序,直接从左往右插入即可。
int n, a[N];
int l[N], r[N]; // 左右儿子
int stk[N], top; // 右链
cin >> n;
for (int i = 1; i <= n; ++ i ) {
cin >> a[i];
int k = top;
while (top && a[stk[top]] > a[i]) top -- ;
if (top) r[stk[top]] = i;
if (top < k) l[i] = stk[top + 1];
stk[ ++ top] = i;
}
应用技巧
-
以 \(u\) 为根的子树对应到原序列上是一段区间,且根节点是这段区间的最小/大值(取决于小根堆还是大根堆)。
-
将笛卡尔树中序遍历(左根右)能得到原序列。