\(\texttt{0x00}\):前置芝士
- 二叉搜索树
- 堆
- 单调栈
\(\texttt{0x01}\):概念
笛卡尔树是一种二叉树,每一个结点由一个键值二元组 \((k,w)\) 构成。要求 \(k\) 满足二叉搜索树的性质(左小右大),而 \(w\) 满足堆的性质(大根堆或小根堆)。
q1:这么一看,Treap 不也是笛卡尔树?
a1:正确的。
一个有趣的事实是,如果笛卡尔树的 \(k,w\) 键值确定,且 \(k\) 互不相同,\(w\) 互不相同,那么这个笛卡尔树的结构是唯一的。
q2:那它有什么用,写个 Treap 不是就可以代替它了吗?
a2:它在一些问题上(比如求最大值)的速度比 Treap 快,这就足够了。
\(\texttt{0x02}\):构建
对于一个 \(1\sim n\) 的排列,以下标为键值 \(k\) (满足二叉搜索树性质),数值为键值 \(w\) (满足小根堆的性质),如何建立笛卡尔树?
考虑到笛卡尔树的性质,我们先将整个序列的最小值找出来作为根节点,然后再分别在其左右区间中找到最小值作为左右子树的根节点,依次这样递归下去即可完成建树。
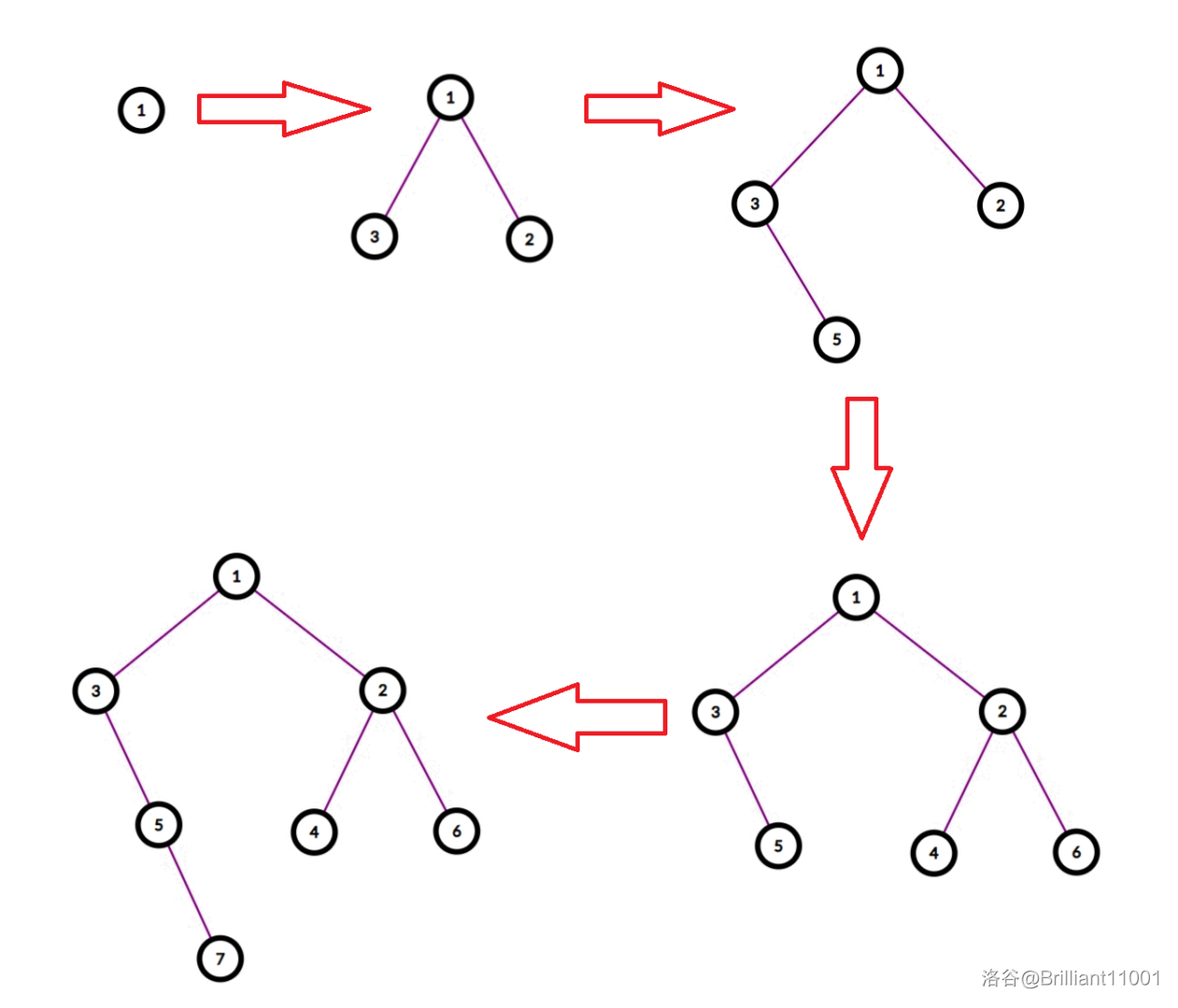
比如一个序列 \(\{3,5,7,1,4,2,6\}\) 它的建树过程如下:
先找到全局最小值 \(1\) 作为根节点。
递归左子树,找到区间 \(\{3,5,7\}\) 中的最小值 \(3\) 作为左子树的根节点。
递归右子树,找到区间 \(\{4,2,6\}\) 中的最小值 \(2\) 作为右子树的根节点。
继续向下递归,找到区间 \(\{5,7\}\) 中的最小值 \(5\) 作为子树根节点。
右子树中左为 \(4\),右为 \(6\)。
\(7\) 挂在 \(5\) 右子树上。
最坏情况下时间复杂度为 \(O(n^2)\),用线段树或 ST 表优化后为 \(O(n\log n)\)。
当然也可以用 Treap 一个一个插入,也是 \(O(n\log n)\)。
注意数据范围:\(n\le 10^7\)。
Treap 一下就释怀地似了。
这要求我们在线性时间复杂度内完成建树操作,怎么办?
回想一下笛卡尔树的性质,发现下标一定是单调递增的,所以我们只会在右子树上插入新的节点!
考虑一下每个点插入时的情形:
当我们插入一个点 \(i\) 时,实际上就是在右链上找到一个一个位置,使得 \(w_u\) < \(w_i\) < \(w_v\),然后我们将 \(u\) 的右儿子修改成 \(i\),\(i\) 的左儿子修改为 \(v\)。
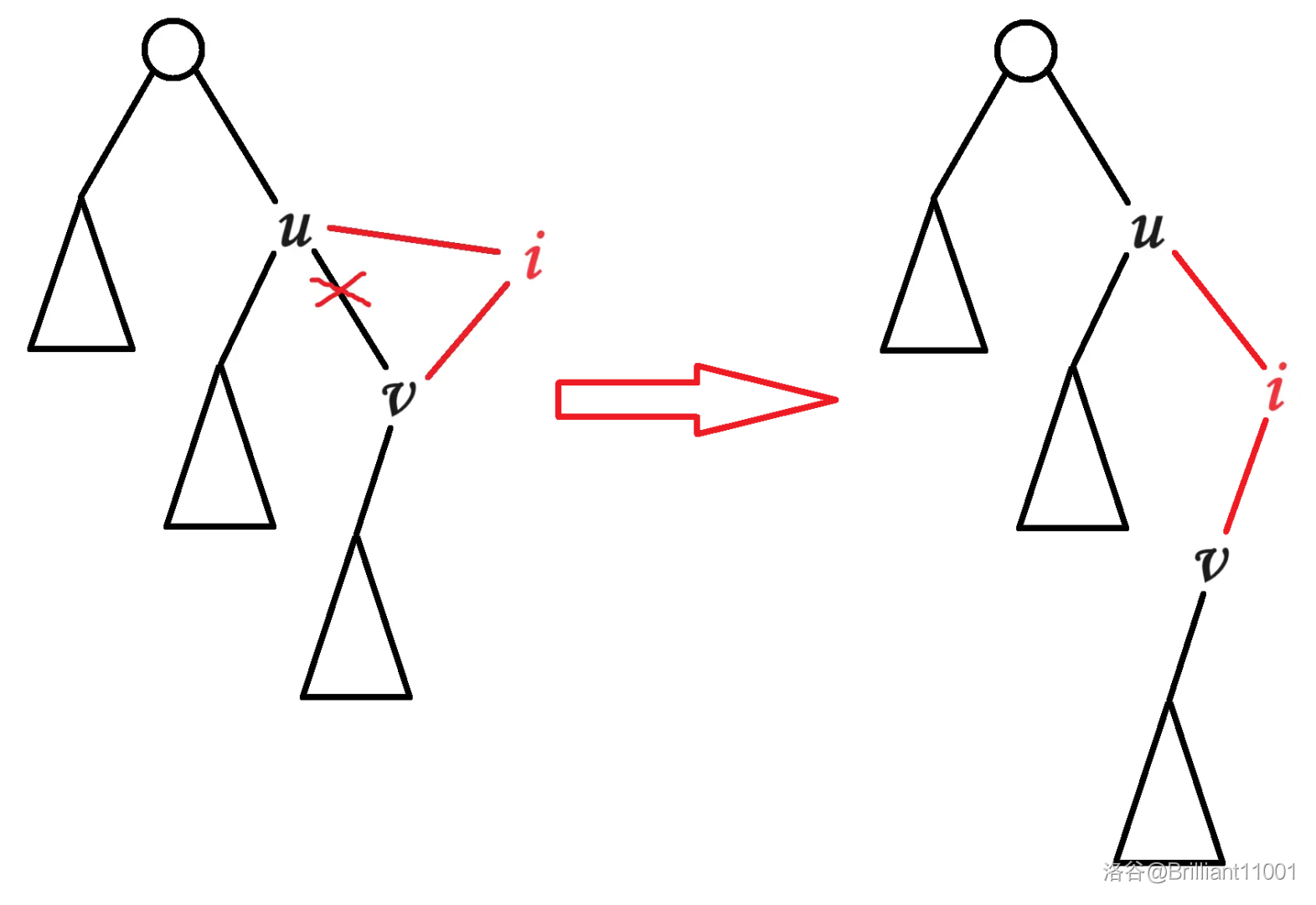
这启示我们只需要维护这个右链,显然可以用单调栈维护。
若新加的点小于栈顶,则弹出,直到栈为空或栈顶比它大。
注意这里要特判一下,若栈已经为空了,说明当前点要作为根节点,所以要把根节点更新,并且不用将栈顶的右儿子修改为 \(i\)。
用插入的方式理解一下上述例子:
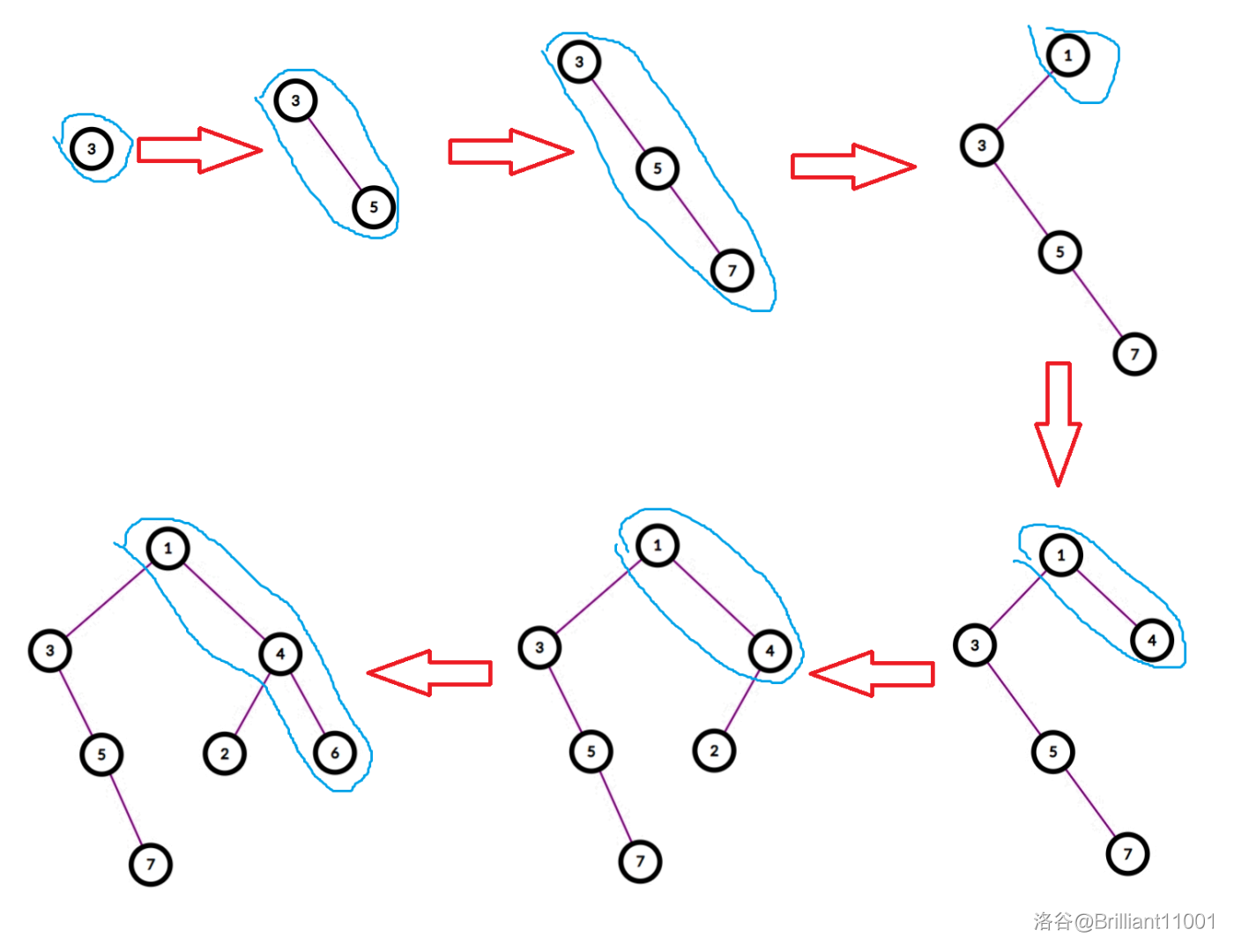
其中蓝色框起来的部分就是维护的右链。
\(\texttt{Code}\):
#include <iostream>
using namespace std;
const int N = 10000010;
int n;
int a[N];
int stk[N], top;
struct node{
int ls, rs;
}tr[N];
int root;
inline int read() {
int x = 0;
char ch = getchar();
while(ch < '0' || ch > '9') ch = getchar();
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + ch - 48; ch = getchar();}
return x;
}
void build() {
for(int i = 1; i <= n; i++) {
int las = 0;
while(top > 0 && a[stk[top]] >= a[i]) las = stk[top--];
if(!top) root = i;
if(top) tr[stk[top]].rs = i;
tr[i].ls = las;
stk[++top] = i;
}
}
int main() {
n = read();
for(int i = 1; i <= n; i++) a[i] = read();
build();
long long res1 = 0, res2 = 0;
for(int i = 1; i <= n; i++)
res1 ^= 1ll * i * (tr[i].ls + 1), res2 ^= 1ll * i * (tr[i].rs + 1);
printf("%lld %lld\n", res1, res2);
return 0;
}
题目大意:
根据生成序列建出一棵笛卡尔树,求一个字典序最小且和它能得到相同笛卡尔树的生成序列。
思路:
先解释一下为什么是建出一颗笛卡尔树。
首先键值 \(k\) 满足 BST 性质,其次它是一个一个插入到子树里的,所以如果建立一个时间戳,父节点的时间戳一定小与子节点,这就满足堆性质,可以把时间戳当成笛卡尔树中的第二个键值,所以是建一棵笛卡尔树。
所以接下来思路就很明显了,我们先建一棵小根堆笛卡尔树,由于要字典序最小,所以我们得把尽量小的点往左子树里塞,具体操作就是对该笛卡尔树进行先序遍历,直接输出遍历到的每个点即可。
只需要在模板题的代码上加一个 dfs 就行了。
时间复杂度为 \(O(n)\)。
\(\texttt{Code}\):
#include <iostream>
using namespace std;
const int N = 100010;
int n;
int a[N];
int stk[N], top;
struct node{
int ls, rs;
}tr[N];
int root;
inline int read() {
int x = 0;
char ch = getchar();
while(ch < '0' || ch > '9') ch = getchar();
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + ch - 48; ch = getchar();}
return x;
}
void dfs(int u) {
printf("%d ", u);
if(tr[u].ls) dfs(tr[u].ls);
if(tr[u].rs) dfs(tr[u].rs);
}
void build() {
for(int i = 1; i <= n; i++) {
int las = 0;
while(top > 0 && a[stk[top]] >= a[i]) las = stk[top--];
if(!top) root = i;
if(top) tr[stk[top]].rs = i;
tr[i].ls = las;
stk[++top] = i;
}
dfs(root);
}
int main() {
n = read();
for(int i = 1; i <= n; i++) a[read()] = i;
build();
return 0;
}