BatchNorm & LayerNorm

• BatchNorm & LayerNorm
  • BatchNorm
    • 过程
  • LayerNorm

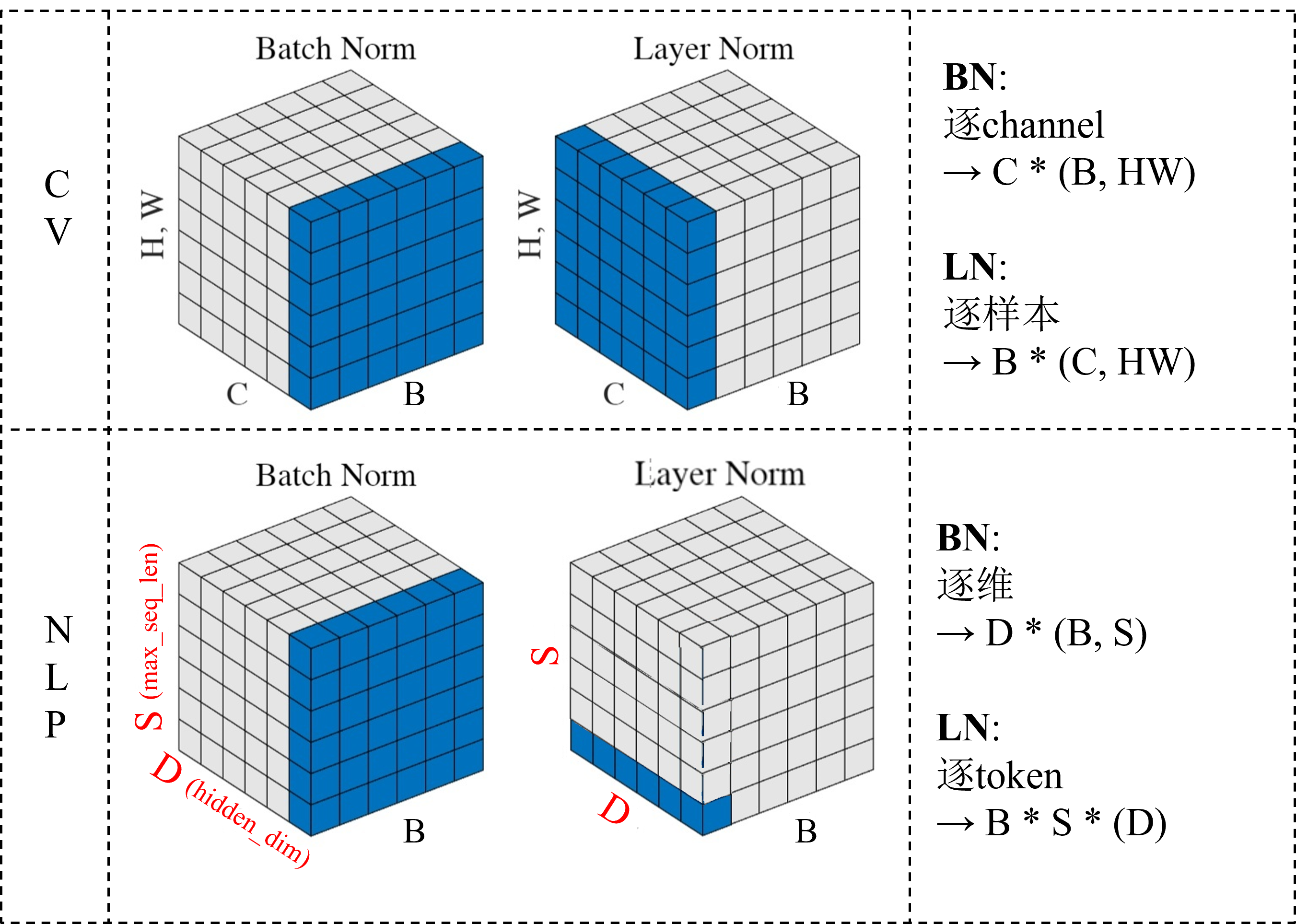
Normalization作用：
1.缓解内部协变量偏移。 在深度神经网络中，随着网络层数的加深，每一层的参数更新都可能导致后续层的输入分布发生变化，这种现象被称为内部协变量偏移（Internal Covariate Shift, ICS）。ICS会导致网络训练困难，因为每一层都需要不断适应新的输入分布。LayerNorm通过归一化每一层的输入，减少了层与层之间的输入分布变化，从而有效缓解了ICS问题。
2. 加速收敛速度。 由于输入数据被归一化到较小的范围内，使得激活函数在其饱和区域内的概率减少，从而减少了梯度消失问题，使得网络更容易学习。
3. 增加模型的泛化性能。 Normalization 类似于一种正则化的方式，使得网络对输入数据的小扰动更加鲁棒，从而提高了模型的泛化能力。

BatchNorm

过程

训练阶段：

1. 计算均值和方差：
   在训练阶段，对于每个 mini-batch，计算当前 mini-batch 上的均值和方差。

2. 归一化：
   使用当前 mini-batch 的均值和方差对特征进行归一化。

3. 更新运行时统计量：
   使用指数加权移动平均更新整个训练集的均值和方差，用于在测试阶段进行归一化。

4. 调整缩放和平移参数：
   在训练阶段，学习并调整批量归一化层中的缩放和平移参数（gamma 和 beta）。

测试阶段：

1. 使用运行时统计量：
   在测试阶段，不再计算当前 mini-batch 的均值和方差，而是使用训练阶段累积的整个训练集的均值和方差。
2. 归一化：
   使用训练阶段累积的均值和方差对特征进行归一化。
3. 应用缩放和平移参数：
   使用训练阶段学习到的缩放和平移参数对归一化后的特征进行缩放和平移。

BatchNorm 中各变量维度如下：

• 当输入维度为 \((N, D)\) 时
  均值（mean）和方差（variance）：维度为 \((D,)\)，即每个维度上的均值和方差。
  归一化后的特征：维度与输入相同 \((N, D)\)。
  缩放因子(gamma)和平移因子(beta)：维度也为 \((D,)\)，即每个维度上的缩放和平移参数。
• 当输入维度为 \((N, H, W, C)\) 时（CV）
  均值（mean）和方差（variance）：维度为 \((C,)\)，即每个通道上的均值和方差。
  归一化后的特征：维度与输入相同 \((N, H, W, C)\)。
  缩放因子(gamma)和平移因子(beta)：维度也为 \((C,)\)，即每个通道上的缩放和平移参数。
• 当输入维度为 \((N, S, D)\) 时（NLP）
  NLP 中的 BN 很模糊，因为一般在 NLP 中不使用 BN，有说输入应该是 \((N, D, S)\) 维度的，按照最上面的图来看：
  均值（mean）和方差（variance）：维度为 \((D,)\)，即每个维度上的均值和方差。
  归一化后的特征：维度与输入相同 \((N, S, D)\) 或 \((N, D, S)\) 。
  缩放因子(gamma)和平移因子(beta)：维度也为 \((D,)\)，即每个维度上的缩放和平移参数。

实现代码(GPT)
由于 NLP 中的 BN 比较模糊，所以没有实现 NLP 中的 BN

import torch

class BatchNorm(torch.nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1):
        super(BatchNorm, self).__init__()
        self.num_features = num_features
        self.eps = eps
        self.momentum = momentum
        self.gamma = torch.nn.Parameter(torch.ones(num_features))
        self.beta = torch.nn.Parameter(torch.zeros(num_features))
        self.register_buffer('running_mean', torch.zeros(num_features))
        self.register_buffer('running_var', torch.ones(num_features))

    def forward(self, x):
        if self.training:
            mean = x.mean(dim=(0, 2, 3), keepdim=True)
            var = x.var(dim=(0, 2, 3), unbiased=False, keepdim=True)
            self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * mean.squeeze()
            self.running_var = self.momentum * self.running_var + (1 - self.momentum) * var.squeeze()
        else:
            mean = self.running_mean
            var = self.running_var
        
        x_normalized = (x - mean) / torch.sqrt(var + self.eps)
        out = self.gamma.view(1, -1, 1, 1) * x_normalized + self.beta.view(1, -1, 1, 1)
        return out

LayerNorm

LayerNorm 常在 NLP 中使用，并且在 NLP 中使用的时候更像是 InstanceNorm，相当于是对每个词向量自身(token)做 norm

LayerNorm 中各变量维度如下：

• 当输入维度为 \((N, D)\) 时
  均值（mean）和方差（variance）：维度为 \((N,)\)，即每个样本的均值和方差。
  归一化后的特征：维度与输入相同 \((N, D)\)。
  缩放因子(gamma)和平移因子(beta)：维度也为 \((N,)\)，即每个样本的缩放和平移参数。
• 当输入维度为 \((N, H, W, C)\) 时（CV）
  均值（mean）和方差（variance）：维度为 \((N,)\)，即每个样本的均值和方差。
  归一化后的特征：维度与输入相同 \((N, H, W, C)\)。
  缩放因子(gamma)和平移因子(beta)：维度也为 \((N,)\)，即每个样本的缩放和平移参数。
• 当输入维度为 \((N, S, D)\) 时（NLP）
  均值（mean）和方差（variance）：维度为 \((N, S,)\)，即每个样本的各个 token 的均值和方差。
  归一化后的特征：维度与输入相同 \((N, S, D)\) 。
  缩放因子(gamma)和平移因子(beta)：维度也为 \((N, S, )\)，即每个样本的各个 token 的缩放和平移参数。

实现代码

import torch

class LayerNorm(torch.nn.Module):
    def __init__(self, features, eps=1e-5, momentum=0.1):
        super(LayerNorm, self).__init__()
        self.features = features
        self.eps = eps
        self.momentum = momentum
        self.gamma = torch.nn.Parameter(torch.ones(features))
        self.beta = torch.nn.Parameter(torch.zeros(features))
        self.register_buffer('running_mean', torch.zeros(features))
        self.register_buffer('running_std', torch.ones(features))

    def forward(self, x):
        if self.training:
            mean = x.mean(dim=-1, keepdim=True)
            std = x.std(dim=-1, unbiased=False, keepdim=True)
            self.running_mean = self.momentum * self.running_mean + (1 - self.momentum) * mean.squeeze()
            self.running_std = self.momentum * self.running_std + (1 - self.momentum) * std.squeeze()
        else:
            mean = self.running_mean
            std = self.running_std

        x_normalized = (x - mean) / torch.sqrt(std**2 + self.eps)
        out = self.gamma * x_normalized + self.beta
        return out