LayerNorm 等其他归一化

标签：方差 LN 均值 batch Batch 其他归一化 LayerNorm

LayerNorm 等其他归一化

总览

BatchNorm：沿batch方向上，对 (N、H、W) 做归一化，保留通道C的维度

适用于CNN
对小batchsize效果不好；BN主要缺点是对batchsize的大小比较敏感
由于每次计算均值和方差是在一个batch上，所以如果batchsize太小，则计算的均值、方差不足以代表整个数据分布

LayerNorm：沿channel方向上，对 (C、H、W) 做归一化，保留通道N的维度

适用序列模型，如：RNN
不适应输入变化很大的数据，大Batch较差

InstanceNorm：在图像像素上，对 (H、W) 做归一化

优点：适用图像风格迁移，因为生成结果主要依赖于某个图像实例，
HW做归一化。可以加速模型收敛，并且保持每个图像实例之间的独立。
不适应通道之间的相关性较强数据

GroupNorm：将channel分组，对 (C/G、H、W) 做归一化，在不同的Batch Size下具有较大的稳定性

优点：不同Batch Size下具有较大的稳定性
缺点：在大Batch 下性能略差于BN

其他归一化方式

Switchable Normalization（SN，2018年）：将BN、LN、IN结合，赋予权重，让网络自己去学习归一化层

Positional Normalization（PN，2019年）：提出了位置归一化算法来计算生成网络沿信道维数的统计量；

Batch Group Normalization（BGN，2020年）解决Batch Size退化和饱和的问题；

Batch Norm

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

num_features：	来自期望输入的特征数，该期望输入的大小为’batch_size x num_features [x width]’
eps： 			为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。
momentum： 		动态均值和动态方差所使用的动量。默认为0.1。
affine： 		布尔值，当设为true，给该层添加可学习的仿射变换参数。
track_running_stats：布尔值，当设为true，记录训练过程中的均值和方差；

Layer Norm

Layer Normalization的思想与Batch Normalization非常类似，只是Batch Normalization是在每个神经元对一个mini batch大小的样本进行规范化，而Layer Normalization则是在每一层对单个样本的所有神经元节点进行规范化，即C,W,H维度求均值方差进行归一化（当前层一共会求batch size个均值和方差，每个batch size分别规范化）。 LN 不需要批训练，在单条数据内部就能归一化。

论文链接：https://arxiv.org/abs/1607.06450

torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)

normalized_shape： 	输入尺寸
[∗×normalized_shape[0]×normalized_shape[1]×…×normalized_shape[−1]]
eps： 				为保证数值稳定性（分母不能趋近或取0）,给分母加上的值。默认为1e-5。
elementwise_affine： 布尔值，当设为true，给该层添加可学习的仿射变换参数。

计算过程

沿着 batch 方向计算每个通道 (C, H, W) 的均值 $\mu$ 和方差 $ \sigma $
做归一化
引入缩放和平移变量计算最后的归一化数值（平移和缩放）

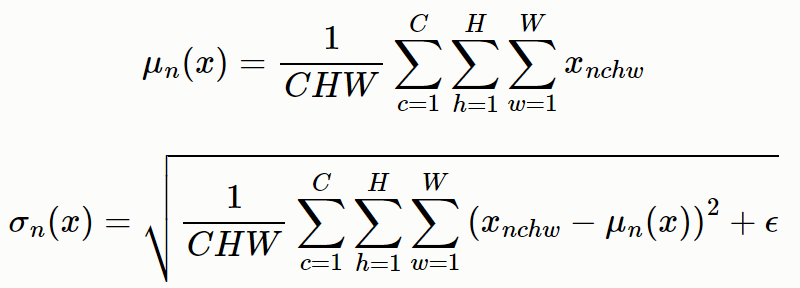
其中前一项是归一化过程。分母中的 $ \epsilon $ 是一个非常小的数，作用是防止数值计算不稳定。 $\gamma$ 和 $\beta $ 是仿射参数，将归一化后的数据再次放缩得到新的数据， $\gamma$ 可以理解为标准差， $\beta $ 可以理解为均值，它们两个一般是可学习的。可以发现，， $\gamma$ 和， $\beta $ 是LayerNorm层仅有的可学习参数。

LN优缺点

LN针对单个训练样本进行，不依赖于其他数据,可以避免BN中受mini-batch数据分布的影响的问题。
LayerNorm中没有batch的概念，所以不会像BatchNorm那样跟踪统计全局的均值方差，因此train()和eval()对LayerNorm没有影响。
LN特别适合处理变长数据，因为是对channel维度做操作(这里指NLP中的hidden维度)，和句子长度和batch大小无关

用法上的差异

nn.BatchNorm2d(num_features)中的num_features一般是输入数据的第2维(从1开始数），BatchNorm中weight和bias与num_features一致。
nn.LayerNorm(normalized_shape)中的 normalized_shape是最后的几维，LayerNorm中weight和bias的shape就是传入的normalized_shape。
输出维度不同，BN 输出维度为C, LN输出维度为 N

transformer 为什么使用 layer norm

测试集中出现比训练集更长的数据，tranformer支持任意长度输入
长短不一的情况下，足够的batch_size的数据，文本数据较图像数据的分布差异更大
可能原因：批归一化会破坏向量的位置信息

Instance Norma, IN

对一个特征图的所有通道做归一化

Group Norma, GN

Group Normalization(GN) 则是提出的一种 BN 的替代方法，Group Normalization 将 channel 分成 num_groups组，每组包含channel / num_groups通道，则feature map变为(N, G, C//G, H, W)，然后计算每组 (C//G, H, W)维度平均值和标准差，这样就与batch size无关。

GB的计算与Batch Size无关，因此对于高精度图片小BatchSize的情况也是非常稳定的

GN是为了解决BN对较小的mini-batch size效果差的问题。GN适用于占用显存比较大的任务，例如图像分割。对这类任务，可能 batch size 只能是个位数

GN的主要思想：在 channel 方向 group，然后每个 group 内做 Norm，计算的均值和方差，这样就与batch size无关，不受其约束。