题面
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
思路
这次我们要使用的知识点是 \(dfs\) 和并查集,这个 \(tarjan\) 是离线的,我们要先把每个点的每一个要跟它求 \(LCA\) 的点给记录下来,接下来用 \(dfs\) 跑这么个流程:
- 遍历这个点的每个子结点并进入子节点
- 将子节点与自己合并
- 遍历要跟它求 \(LCA\) 的点,如果这个点被访问了,这个点在并查集中的祖先便是答案
等等,你是不是蒙圈了?我们先放张图:
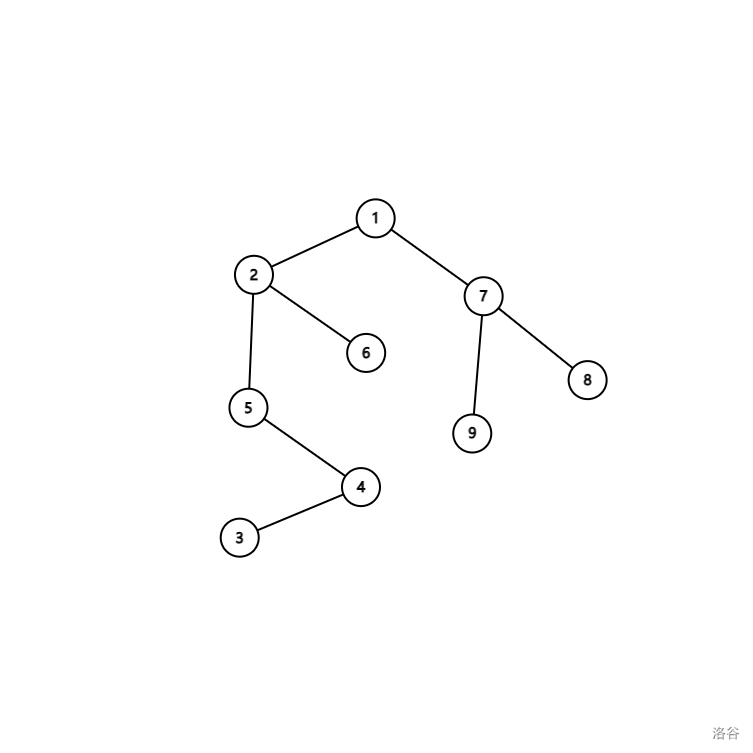
假设我们要求 \(LCA(3,6)\) 。
我们在这张图上模拟一下并查集中的过程:
首先,一切还是一盘散沙:
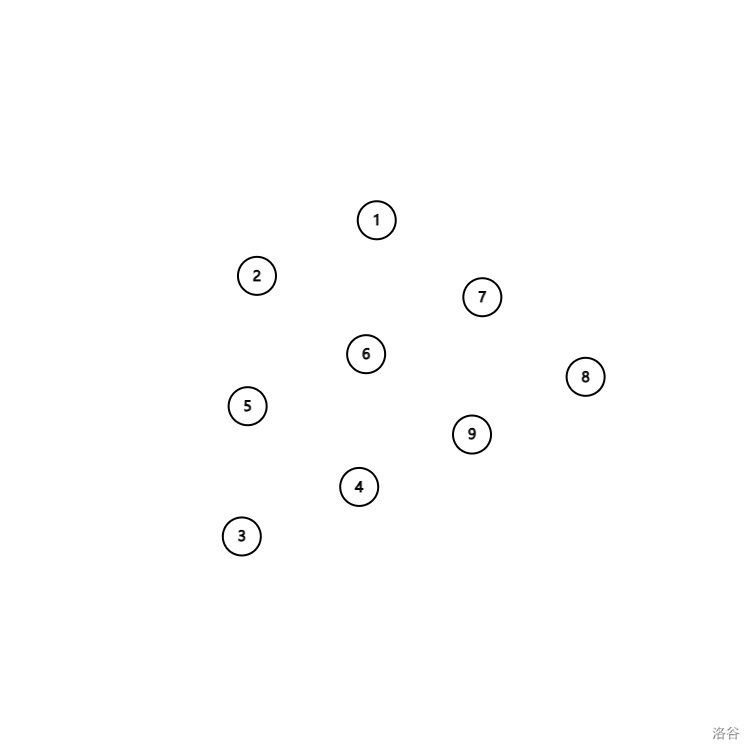
接下来,\(3\) 和它的父节点 \(4\) 合并起来了,由于与 \(3\) 它相关联的 \(6\) 还没访问,此时无法更新任何答案:
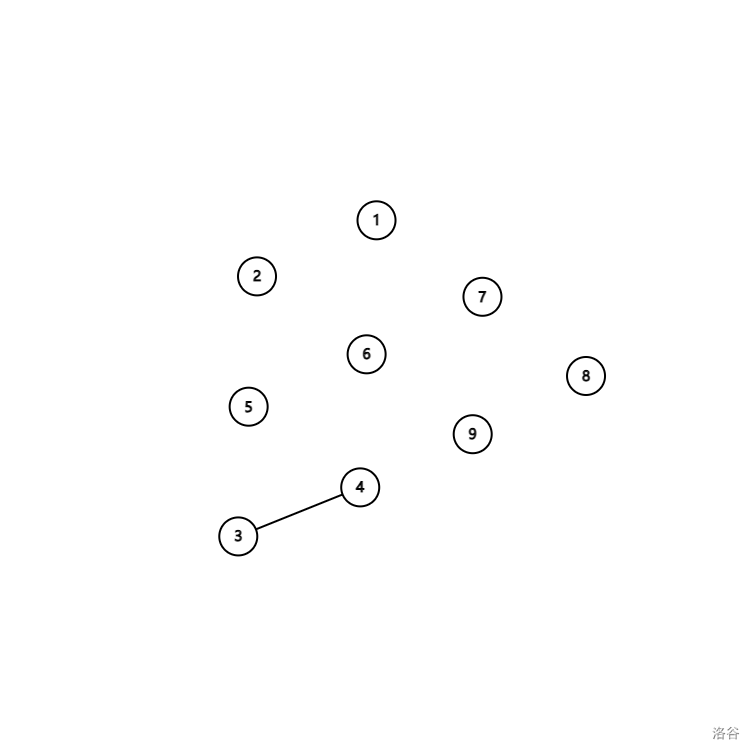
接着又是 \(5,4\) 以及 \(2,5\),都无法更新答案:
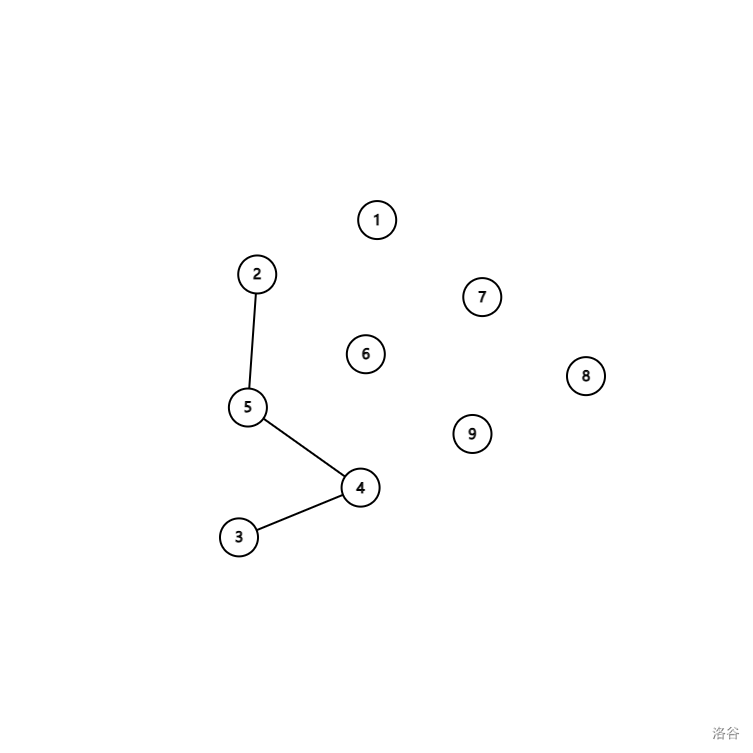
注意了!!!此处敲黑板!!!此时我们访问到 \(2\) 的另一个子节点 \(6\),此时我们便发现,\(3\) 已被访问,于是答案是 \(2\) !!!
后面的无用功就不放了。
于是,我们就发现了,其实我们就是把点按 \(dfn\) 序不断合并,当两个点要合并在一起时,此时的祖先便是答案,就像这样:
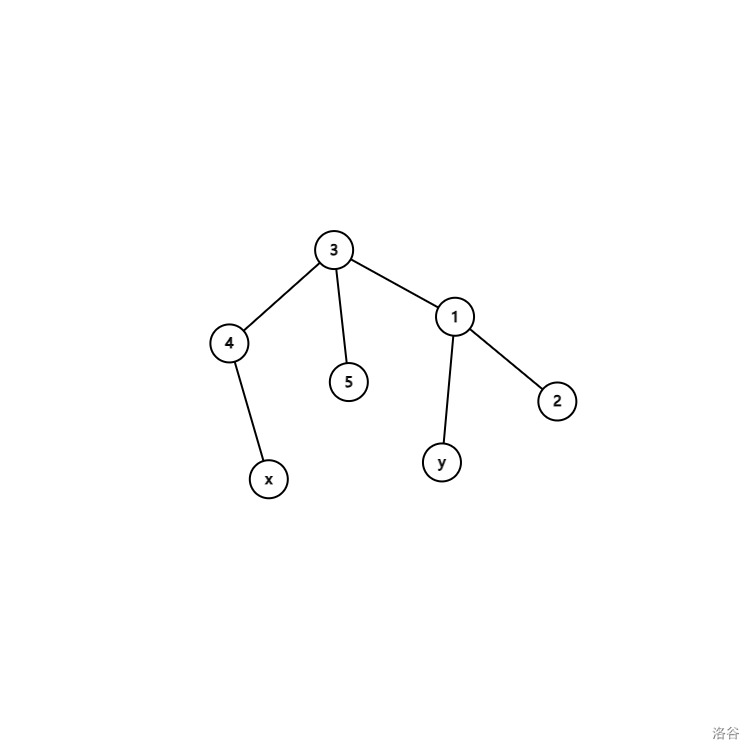
\(x\) 和 \(y\) 便是要求 \(LCA\) 的两个点,它们现在刚好就合并到一起,显然只有到它们的公共祖先它们才会合并在一起,再由于回溯时是从深到低,所以第一次合并在一起时一定是到 \(LCA\) 了。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdio>
#include<string>
#include<iomanip>
using namespace std;
const int N=5e5+10;
int n,m,s;
struct edge{
int to,nxt;
}g[N<<1];
int head[N],tot1=0;
struct qry{
int to,nxt,idx;
}q[N<<1];
int qhead[N],tot2=0;
int ans[N];
void add(int x,int y){
tot1++;
g[tot1].to=y;
g[tot1].nxt=head[x];
head[x]=tot1;
return;
}
void qadd(int x,int y,int z){
tot2++;
q[tot2].to=y;
q[tot2].nxt=qhead[x];
q[tot2].idx=z;
qhead[x]=tot2;
return;
}
int fa[N],vis[N];
int Find(int x){
return (fa[x]==x)?x:(fa[x]=Find(fa[x]));
}
void dfs(int u,int f){
vis[u]=1;
for(int i=head[u];i;i=g[i].nxt){
int v=g[i].to;
if(v!=f){
dfs(v,u);
fa[v]=u;
}
}
for(int i=qhead[u];i;i=q[i].nxt){
int v=q[i].to;
if(vis[v]){
ans[q[i].idx]=Find(v);
}
}
return;
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
cin>>n>>m>>s;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
qadd(u,v,i);
qadd(v,u,i);
}
for(int i=1;i<=n;i++)fa[i]=i;
dfs(s,0);
for(int i=1;i<=m;i++){
cout<<ans[i]<<"\n";
}
cout<<flush;
return 0;
}