标签：limits 线段节点 sum 区间 ll

完成时间： $2024.5.31\sim202?.?.?$

工程表

$日期$	$完工$
$2024.6.1$	$2.3,3.1,3.2,3.3$
$2024.6.5$	$2.1,2.2$
$2024.6.8$	$3.4$

线段树入门

P2068 统计和

P1531 I Hate It

打算写，鸽一鸽。

线段树基础

懒标记线段树

P3372 【模板】线段树 1

如果暴力修改的话，时间复杂度会退化到 $O(n^2)$。

受到第一道例题启发，我们将修改的区间划分成 $\log n$ 个区间。不同的是，我们没必要将这个区间里的每一个数都修改。

例如我们修改了 $[3,4]$，后一次查询操作查询了 $[2,5]$。不过我们遍历到区间 $[3,4]$ 时直接返回了这个区间的 $sum$，而并没有用到 $[3,3],[4,4]$ 的相关信息。我们只需要直接修改 $[3,4]$ 的 $sum$ 值（同理，如果我们要修改一个区间 $[l,r]$ 的信息，以这道题为例，区间加 $k$，区间和就加上了 $(r-l+1)\times k$ ）。就可以保证这几次询问的正确性。

但如果下一次询问要询问 $[1,3]$，需要用到 $[3,3]$ 的信息。但我们只修改了 $[3,4]$ ，却没有修改 $[3,3]$。这岂不穿帮了？所以我们需要在每个节点处维护一个变量，表示
「当前区间已经修改，但其子节点还为修改」的信息。当需要访问一个节点的子节点时，就下传这个变量并清零。

我们令其为 $tag$（下文称之为“懒标记”）。我们只要在将要遍历一个区间的子节点时，将这个区间的 $tag$ 下传给子节点，然后清空。就可以始终保持当前区间处于「所有相关操作均已进行」的状态。

注意的是，修改子节点后，一定要 $\text{push_up}$。

时间复杂度：在线段树中的查询或修改中，深度为 $i$ 的节点向深度为 $i+1$ 的节点下传懒标记的次数不会超过 $2$，深度为 $i$ 的节点通过深度为 $i+1$ 的节点进行 $\text{push_up}$ 的次数也不会超过 $2$ 次。时间复杂度为 $O(n\log n)$。

搞清楚这些，就很好做了：

点击查看代码

ll update(int p){
	return a[2*p].sum+a[2*p+1].sum;
}
void push_down(int p){
	int lt=2*p,rt=2*p+1;
	a[lt].lazy+=a[p].lazy;a[lt].sum+=(a[lt].right-a[lt].left+1)*a[p].lazy;
	a[rt].lazy+=a[p].lazy;a[rt].sum+=(a[rt].right-a[rt].left+1)*a[p].lazy;
	a[p].lazy=0;
}	
void add(int l,int r,int t,int p){
	if(a[p].left>=l&&a[p].right<=r){
		a[p].lazy+=t;
		a[p].sum+=(a[p].right-a[p].left+1)*t;
	}else{
		push_down(p);
		int mid=(a[p].left+a[p].right)/2;
		if(l<=mid)add(l,r,t,2*p);
		if(r>mid)add(l,r,t,2*p+1);
		a[p].sum=update(p);
	}
	return;
}
ll sum(int l,int r,int p){
	if(a[p].left>=l&&a[p].right<=r)return a[p].sum;
	push_down(p);
	ll v=0,mid=(a[p].left+a[p].right)/2;
	if(l<=mid)v+=sum(l,r,2*p);
	if(r>mid)v+=sum(l,r,2*p+1);
	return v;
}

P3373 【模板】线段树 2

本题增加了一个区间乘的操作，关键在于如何记录加和乘的信息，将其下传给子节点。

我们发现一个 $tag$ 难以维护，于是我们定义两个 $tag$，分别是 $mul$ 和 $add$。代表的意义是「整个区间先乘了 $mul$，然后加了 $add$」。

如果区间加 $k$：此时整个区间先乘了 $mul$，然后加了 $add$，最后加了 $k$，等价于整个区间先乘了 $mul$，然后加了 $add+ k$。

所以我们直接把 $k$ 加到 $add$ 里，同时更新 $sum$。

如果区间乘 $k$：此时整个区间先乘了 $mul$，然后加了 $add$，最后乘了 $k$，等价于整个区间先乘了 $mul\times k$，然后加了 $add\times k$。

所以令 $mul\to mul\times k,add\to add\times k$。

时间复杂度 $O(n\log n)$。

点击查看代码

void push_down(ll p,ll ls,ll rs){
    if(a[p].tag2!=1){
        a[ls].tag2=(a[ls].tag2*a[p].tag2)%mod;
        a[rs].tag2=(a[rs].tag2*a[p].tag2)%mod;
        a[ls].tag1=(a[ls].tag1*a[p].tag2)%mod;
        a[rs].tag1=(a[rs].tag1*a[p].tag2)%mod;
        a[ls].sum=(a[ls].sum*a[p].tag2)%mod;
        a[rs].sum=(a[rs].sum*a[p].tag2)%mod;
        a[p].tag2=1;
    }
    if(a[p].tag1){
        a[ls].tag1=(a[ls].tag1+a[p].tag1)%mod;
        a[rs].tag1=(a[rs].tag1+a[p].tag1)%mod;
        a[ls].sum=(a[ls].sum+((a[ls].r-a[ls].l+1)*a[p].tag1)%mod)%mod;
        a[rs].sum=(a[rs].sum+((a[rs].r-a[rs].l+1)*a[p].tag1)%mod)%mod;
        a[p].tag1=0;
    }
}

P1471 方差

我们先思考区间平均数如何做。显然，如果我们可以快速求出区间和，然后除以区间长度就可以了，就是线段树1。

对于区间方差，我们推一下式子

\[\begin{aligned} s^2&=\frac{1}{n}\sum\limits_{i=1}^n\left(A_i-\overline A\right)^2\\ &=\frac{1}{n}\sum\limits_{i=1}^n\left(A_i^2-2A_i\overline A+\overline A^2\right)\\ &=\frac{1}{n}\sum\limits_{i=1}^nA_i^2-2\overline A\times \overline A+\overline A^2\\ &=\frac{1}{n}\sum\limits_{i=1}^nA_i^2-\overline A^2 \end{aligned} \]

显然，我们只需要维护 $\sum\limits_{i=1}^nA_i$ 和 $\sum\limits_{i=1}^nA_i^2$。前者好维护（下文令其为 $sum$），但后者（下文令其为 $exsum$）在区间加情况下不易维护，我们在推再下式子。

\[\begin{aligned} \sum\limits_{i=1}^n(A_i+k)^2-\sum\limits_{i=1}^nA_i^2 &=\sum\limits_{i=1}^n\left(A_i^2+2A_ik+k^2\right)-\sum\limits_{i=1}^nA_i^2\\ &=\sum\limits_{i=1}^nA_i^2+2k\sum\limits_{i=1}^nA_i+nk^2-\sum\limits_{i=1}^nA_i^2\\ &=2k\sum\limits_{i=1}^nA_i+nk^2\\ &=2k·sum+nk^2 \end{aligned}\\ \]

具体来说，如果其父节点下传懒标记 $tag$ 给子节点 $[l,r]$，则其子节点

\[exsum'=exsum+2·tag·sum+(r-l+1)\times tag^2 \]

这样只用一个 $tag$ 就可以维护两个变量了。

权值线段树

就是线段树维护值域。

P1774 最接近神的人

我们知道，冒泡排序的过程会进行 $n-1$ 次循环，每次从前往后枚举 $p$，遇到 $a_p>a_{p+1}$ 就交换着两个数，最后序列就会变得有序，我们就可以得出结论

在一个序列列 $A$ 中，定义一个二元组 $(i,j)$ 为“逆序对”，必须满足 $i<j$ 且 $A_i>A_j$

进行一种操作，交换序列中相邻的两个元素。而用最少的，使原序列变成不下降序列的的次数即为这个序列中逆序对的个数

如何快速求解逆序对问题？

我们从后往前枚举 $i$，对于以 $i$ 开头的逆序对的个数，就是存在多少 $j$ 使得 $i<j,A_i>A_j$。我们使用一个权值数组 $val$，$val_k$ 表示 $k$ 在 $[i+1,n]$ 中的出现次数。

那么以 $i$ 开头的逆序对的个数即为 $\sum\limits_{l=1}^{A_i-1}val_l$，因为此时 $val$ 数组中的所有数下表均大于 $i$，只要满足小于 $A_i$ 的条件即可。

求值完之后可以修改 $val$ 数组，时间复杂度 $O(n^2)$。可以用线段树代替数组将复杂度优化到 $O(n\log n)$。

P1637 三元上升子序列

介绍两种做法。

1. 枚举中间数：

我们枚举中间数 $j$，求两个数组，分别是 $le_j$ 和 $ri_j$。

$le_j$：存在多少 $i$，使得 $i<j,A_i>A_j$。

$ri_j$：存在对少 $k$，使得 $j<k,A_j>A_k$。

实质上是两次逆序对。由乘法原理可得答案为

\[\sum\limits_{k=1}^nle_k\times ri_k \]

2.逐步递推：

我们定义 $f_{i,j}$ 表示以 $i$ 结尾的 $j$ 元上升子序列。根据乘法原理可得

\[f_{i,j}=\sum\limits_{k=1}^{i-1}f_{k,j-1}[A_k<A_j] \]

初始化任意 $f_{i,1}=1$。我们逐步递推，本题只需推到出所有 $f_{i,3}$。这种做法可以推广到 $k$ 元上升子序列，时间复杂度 $O(kn\log n)$。

P6186 [NOI Online #1 提高组] 冒泡排序

如果对于一个数 $p_j$ 存在 $i<j,p_i>p_j$，那么这轮冒泡排序无论如何都会使 $p_j$ 被交换，在 $p_j$ 之前比 $p_j$ 大的数只会消失一个。

换言之，令 $f_j$ 表示以 $j$ 结尾的逆序对数量，在进行 $k$ 轮冒泡排序后 $f_j'=\max\{0,f_j-k\}$。

而交换两个数无非对两个数的 $f_j$ 造成影响，我们预处理出 $f_i$，转换题意。

你需写一个数据结构维护 $f$，支持两种操作。

给定 $k$，求出 $\sum\limits_{i=1}^n{\max\{0,f_i-k}\}$

给定 $x$ 和 $t$，令 $f_x\to f_x+t,t\in \{1,-1\}$

显然，每次询问中 $f_i\le k$ 的 $f_i$ 不会在答案中有贡献。我们令 $cnt_x$ 表示存在多少个 $i$ 使得 $f_i=x$。则所有 $f_i>k$ 的 $f_i$ 的和即为 $\sum\limits_{x=k+1}^ncnt_x\times x$。因为这些数每个数都减去 $k$，所以减去 $\sum\limits_{x=k+1}^ncnt_x\times k=k\sum\limits_{x=k+1}^ncnt_x$。

单点修改 $f_i$ 就是单点修改 $cnt_x$。问题变成区间查询 $\sum\limits_{x=l}^rcnt_x\times x,\sum\limits_{x=l}^rcnt_x$。

可以用线段树快速维护。时间复杂度 $O(n\log n)$。

特殊维护方法

P4513 小白逛公园

直接维护显然无法做到，不过可以分开来维护。

思考区间 $[l,r]$ 的最大子段在那个位置，无非三种

最大子段在 $[l,mid]$ 中：即左节点的最大子段。
最大子段在 $[mid+1,r]$：中，即右节点的最大子段。
包含 $mid,mid+1$：即最大子段可分成两部分，分别是 $[L,mid]$ 和 $[mid+1,R]$，$[L,R]$ 即表示最大子段

第三种情况下，因为 $[L,R]$ 最大，所以 $[L,mid]$ 是左节点最大后缀，$[mid+1,R]$ 则是右节点最大前缀。

所以我们还要维护区间最大前后缀，无非两种情况，我们就最大前缀来讲，假设区间 $[l,r]$ 的最大前缀是 $[l,R]$

$R\le mid$：即左子节点最大前缀。
$R > mid$：将最大前缀分为 $[l,mid],[mid+1,R]$，前一个是左子节点区间和，后一个是右子节点最大前缀。

我们同时维护区间和，区间最大前缀，区间最大后缀，区间最大子段，下文分别用 $sum,lmax,rmax,mmax$ 来表示，$p,l,r$ 分别是一个节点和他的左右两个子节点。则

\[sum_p=sum_l+sum_r \]

\[lmax_p=\max\{lmax_l,sum_l+lmax_r\} \]

\[rmax_p=\max\{rmax_r,sum_r+rmax_l\} \]

\[mmax_p=\max\{mmax_l,mmax_r,rmax_l+lmax_r\} \]

P1558 色板游戏

注意到虽然是区修，但颜色很少，所以可以开 $30$ 颗线段树，每颗线段树代表一种颜色。每次修改和查询都跑三十遍就好了。

但显然不够优秀，我们发现题目只关注颜色是否出现，首次启发，对于每个区间 $[l,r]$，压缩一个二进制串，如果这个串第 $i$ 个数为 $1$，则表示这种颜色在区间中出现，$0$ 则反之。

显然易见，该信息具有区间可加性，$\text{push\_up}$ 用或运算就可以完成。

线段树提高

动态开点

线段树在维护值域时会有一个痛点，如果值域很大，把线段树建出来会空间超限。针对这个问题，我们可以使用动态开点的技巧，即在使用时建出要使用的节点。

P5459 [BJOI2016] 回转寿司

求出 $a$ 的前缀和数组 $S$，则 $\sum\limits_{i=l}^ra_i=S_r-S_{l-1}$。我们枚举 $S_r$，即求出

\[L\le S_r-S_{l-1}\le R \]

化简的

\[S_r-R\le S_{l-1}\le S_r-L \]

求出存在多少 $l-1(l>1)$，满足 $l-1< r$ 且 $S_{l-1}\in[S_r-R, S_r-L]$，显然可以使用权值线段树解决。

数据最大可以达到 $10^{10}$，使用动态开点，则树高可达到 $34$，一次修改最多增加 $34$ 个节点，数组开 $3.4\times 10^6$ 大小足矣。

ll New(){
    a[++tot]=node{0,0,0};
    return tot;
}//动态新建节点
void insert(ll p,ll l,ll r,ll x){
    if(l==r)return a[p].sum++,void();//到达最底部
    ll mid=(l+r)>>1;
    if(x<=mid){
        if(!a[p].lc)a[p].lc=New();//插入时不处在，动态开点
        insert(a[p].lc,l,mid,x);
    }else if(x>mid){
        if(!a[p].rc)a[p].rc=New();
        insert(a[p].rc,mid+1,r,x);
    }
    a[p].sum=a[a[p].lc].sum+a[a[p].rc].sum;
}
int ask(ll p,ll l,ll r,ll L,ll R){
    if(L<=l&&r<=R)return a[p].sum;
    ll mid=(l+r)>>1,cnt=0;
    if(L<=mid)cnt+=(!a[p].lc)? 0:ask(a[p].lc,l,mid,L,R);//查询时不存在，直接返回0.
    if(R>mid)cnt+=(!a[p].rc)? 0:ask(a[p].rc,mid+1,r,L,R);
    return cnt;
}

标记永久化

在写线段树的过程中，有时我们很难 $\text{push\_up}$，例如二维线段树或树套树，无法再较短时间内 $\text{push\_up}$。或有时一个节点同时是多个节点的子节点，例如可持久化线段树，我们无法懒标记下传。

针对一些特殊的信息维护，我们可以使用“标记永久化”这种技巧，即给节点打上标记后不在下传，而是在查询时，将该节点到根节点路径上所有节点的标记累加起来。例如区间最大值，区间和等等。

这样做既可以解决无法使用懒标记的问题，还可以进一步优化常数，一举两得，缺点是必须要求打上标记的结果与打上标记的顺序无关。

势能线段树

P4145 上帝造题的七分钟 2 / 花神游历各国

思考一个问题，如果一个数 $x(x>2)$ 不断执行 $x\to x^2$。显然 $x$ 的增长成指数级，相反的，如果一个数 $x$ 不断的执行 $x\to \lfloor\sqrt x\rfloor$ 直至 $x$ 为 $1$。那么操作次数理论在 $\log n$ 这个级别，实际上更少。

这启发我们对于每个不为 $1$ 的数暴力开平方，则修改操作的时间复杂度就是 $O(n\log n)$，我们要同时维护区间和，很容易想到线段树。

如果对区间 $[l,r]$ 中每个数均开方，但区间内每个数均为 $1$，开平方就没有意义（修改后任何值无变化），因此维护区间最大值，只要这个值大于 $1$，就将其暴力修改。

这样看似时间复杂度 $O(n^2)$，实际上只有 $O(n\log n)$，这种特殊的分析方法叫做势能分析法。

CF438D The Child and Sequence

一个结论：$x \bmod p< \frac{x}{2}(x\ge p)$。证明如下：

$p\le \frac{x}{2}$

因为 $x\bmod p <p$，所以 $x\bmod p<\frac{x}{2}$

$\frac{x}{2}<p\le x$

变形可得 $2p>x$，则 $x\bmod p=x-p$，因为 $\frac{x}{2}<p$，所以 $x\bmod p<\frac{x}{2} $

维护区间最大值，照样做就行。

虽然有单点修改，但不同的数最多仍只有 $10^5$ 级别个，不影响时间复杂度。

扫描线

面积并，周长并以及二维数点问题。

P5490 【模板】扫描线

经典面积并。

直接算无从下手，不过我们可以快速分割图形。将一坨分成若干矩形分开来算（依据所有矩形的左右边所在直线划分，下图省略了重复的线）

分割图形

然后维护一根线，从左边走到右边。这就是扫描线求面积并的核心思想。

扫描线

我们把一个矩形 $(x_1,y_1),(x_2,y_2)$ 分成两个四元组 $(x_1,y_1,y_2,1),(x_2,y_1,y_2,-1)$ 分别表示矩形的左右两边。

当扫描线经过一个四元组时，扫描线在矩形并中的部分可能会增加。具体说，如果当前扫描线遇到一个 $(x_1,y_1,y_2,1)$ 的四元组，且扫描线中不包含 $(y_1,y_2)$ 这一部分，那扫描线所截线段长就会加上这一部分；如果当前扫描线遇到一个 $(x_1,y_1,y_2,-1)$ 的四元组，且扫描线中包含 $(y_1,y_2)$ 这一部分，那扫描线所截线段长就会减去这一部分。

我们把所有四元组的 $y$ 放在一起排序，则 $c_i$ 表示 $y_i\sim y_{i-1}$ 这一段区间，如下图。

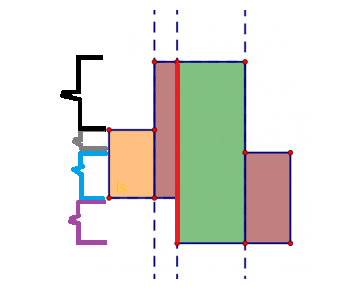
则遇到四元组的操作可以写为区间加，这样就可以用线段树维护截线长了。

然后就做好了，时间复杂度 $O(n\log n)$。

for(int i=1;i<=2*n-1;i++){
	ll L=lower_bound(raw+1,raw+1+tot,b[i].y1)-raw;
	ll R=lower_bound(raw+1,raw+1+tot,b[i].y2)-raw;
	if(L>R)swap(L,R);
	add(1,L,R-1,b[i].k);
    ans+=a[1].dat*(b[i+1].x-b[i].x);
}

P1972 [SDOI2009] HH的项链

经典二维数点。

记一个数 $a_i$ 上一次出现的位置为 $pre_i$（$a_i$ 第一次出现，则 $pre_i=0$）。

一个数在区间 $[l,r]$ 中可以出现很多次，我们只关心最后边的个一个，如果存在 $a_i$ 满足 $i\in[l,r],pre_i\in[0,l-1]$，则这个数在区间中出现过。

转化问题，我们令 $(i,pre_i)$ 为坐标系中的一个点，则求出存在多少点在 $(l,0),(r,l-1)$ 所成的矩形之间。

因为可差分，且容易差分，我们将其分为两个询问的差。用扫描线扫，同时维护扫过的点。

然后写完了。