\(\texttt{0x00}\) 一些概念
什么是“流图”?
给定有向图 \(G = \{V, E\}\),若存在 \(r\in V\),满足从 \(r\) 出发能到达 \(V\) 中的所有点,则称 \(G\) 为一个 “流图”,记为 \((G,r)\),其中 \(r\) 称为流图的源点。
在一个流图 \(G = \{V,E\}\) 上从 \(r\) 出发进行 \(\operatorname{dfs}\),每个点只访问一次,就得到了一棵以 \(r\) 为根的树,称为流图 \(G = \{V, E\}\) 的一棵搜索树。
在 \(\operatorname{dfs}\) 的过程中,按照每个节点第一次被访问的顺序,依次给予流图中 \(N\) 个节点 \(1\sim N\) 的整数标记,该标记被称为时间戳,记为 \(dfn[x]\)。
流图中的有向边可分为 \(4\) 类:
- 树枝边,即搜索树上的边,\(x\) 是 \(y\) 的父节点;
- 前向边,即搜索树中 \(x\) 是 \(y\) 的祖先节点;
- 后向边,即搜索树中 \(y\) 是 \(x\) 的祖先节点;
- 横叉边,即除了以上三种情况的边,它一定满足 \(dfn[x] < dfn[y]\)。
什么是有向图的强连通分量?
首先有个前置概念:强连通图,是指一张有向图中任意两个节点 \(x,y\) 都满足既有从 \(x\) 到 \(y\) 的路径,又有从 \(y\) 到 \(x\) 的路径。
有向图中的强连通分量(\(\texttt{Strongly Connected Component})\) 就是指有向图的极大强连通子图,简记为 \(\texttt{SCC}\)。
简单来讲,一个 SCC 就是一个有向图的一个子图,在这个子图中从任意一个节点出发都能到达这个子图中的其他所有节点。
比如:
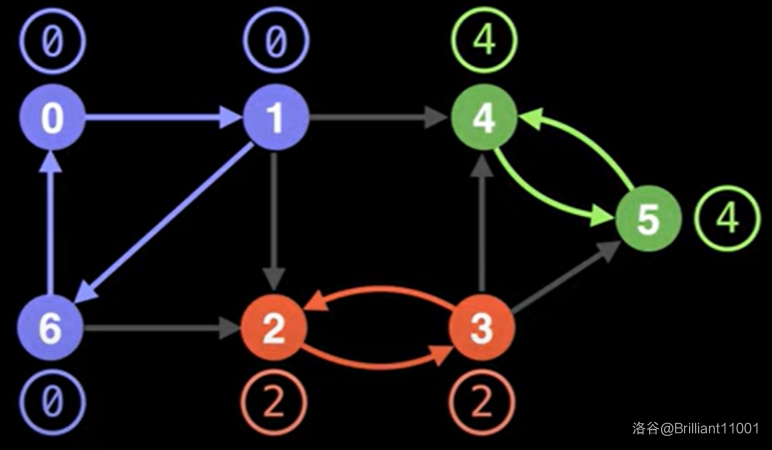
这张有向图中有 \(3\) 个 SCC,如图所示,相同颜色的节点构成这张有向图的一个 SCC。
什么是追溯值?
定义 \(low[x]\) 为 \(x\) 节点的追溯值,则 \(low[x]\) 表示在搜索树中 \(\texttt{subtree(x)}\) 中的所有节点与经过不在搜索树的边,能够到达 \(\texttt{subtree(x)}\) 的节点中的最小 dfn。
简单来讲,就是在对原有向图进行 dfs 时节点 \(x\) 所能到达的所有节点(包括 \(x\) 本身)中时间戳中最小的那个。
比如:
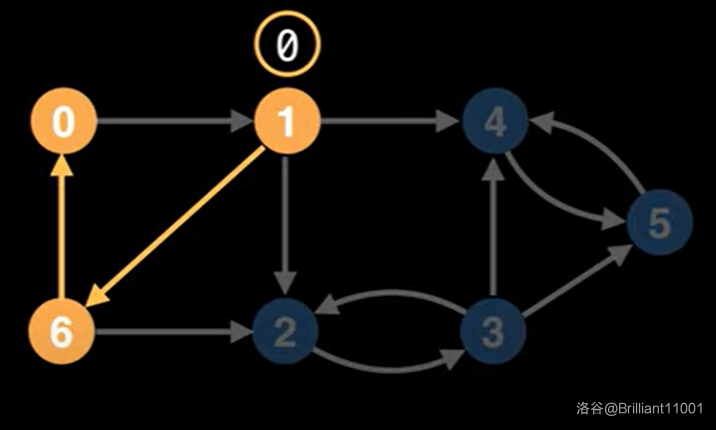
从左上角的节点开始进行 dfs,求出这张有向图中所有节点的 dfn 序,标记在点上。
节点 \(1\) 能到达节点 \(0\) 和节点 \(6\),由于 \(0\) 是节点 \(1\)
所能到达的节点中 dfn 值最小的,所以 \(low[1] = 0\)。
\(\texttt{0x01}\) tarjan 算法求 SCC
tarjan 算法基于有向图的深度优先遍历,能够在 \(O(n + m)\) 的时间复杂度内求出一张有向图的各个 SCC。
思路:
通过定义不难发现:一个环一定是一个强连通图,因此,tarjan 算法就运用了这一点,对于每个点尝试找到与它能构成环的所有节点。
接下来分析每一种边 \((x,y)\):
- 树枝边,作为考虑是否构成环的基础;
- 前向边,因为是由祖先指向子孙,所以一定不会构成环;
- 后向边,非常有用,因为它和搜索树上从 \(y\) 到 \(x\) 的路径构成环;
- 横叉边,看情况,如果经过这条横叉边能走到 \(x\) 的祖先节点上,就是有用的。
综上所述,我们应该寻找“后向边”和“横叉边”和“树枝边”构成的环。
tarjan 算法在执行 dfs 时维护了一个栈。当访问到节点 \(x\) 时,栈中保存了如下节点:
- 搜索树上 \(x\) 的祖先节点,记为 \(anc(x)\)。设 \(y\in anc(x)\),若存在后向边 \((x,y)\),则 \((x,y)\) 与 \(y\) 到 \(x\) 的路径一起构成一个环;
- 已经访问过的,并且存在一条路径到达 \(anc(x)\) 的节点。设 \(z\) 是满足以上性质的节点,若存在横叉边 \((x,z)\),则 \((x,z)\)、\(z\) 到 \(y\) 的路径、\(y\) 到 \(x\) 的路径共同构成一个环。
接着就要用到 SCC 判定法则:若从 \(x\) 回溯前,有 \(dfn[x] = low[x]\) 成立,则从栈顶到 \(x\) 的所有节点构成一个 SCC。
详细的证明在 Tarjan 的论文中,这里主要讲一下怎么理解。
当 \(dfn[x] = low[x]\) 时,\(x\) 就是它所在 SCC 的最高点,即从 \(x\) 出发走不到任何前面的点,所以这时 \(x\) 到栈顶的所有点构成一个 SCC。
举个例子:
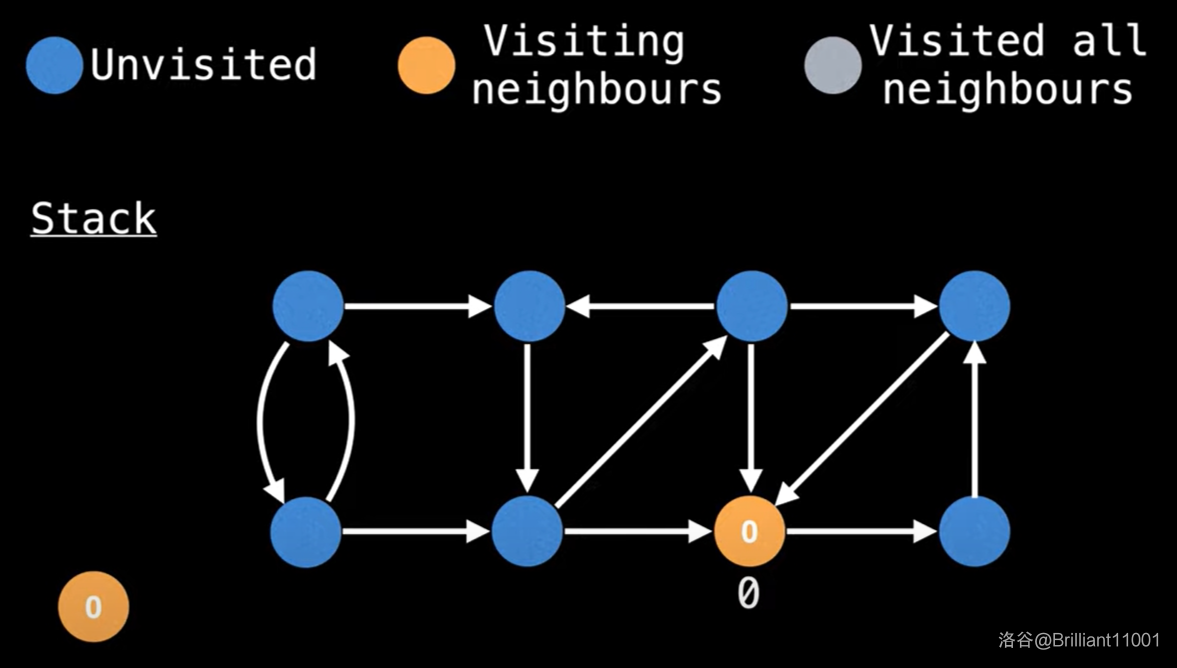
从 \(0\) 号点开始 dfs。
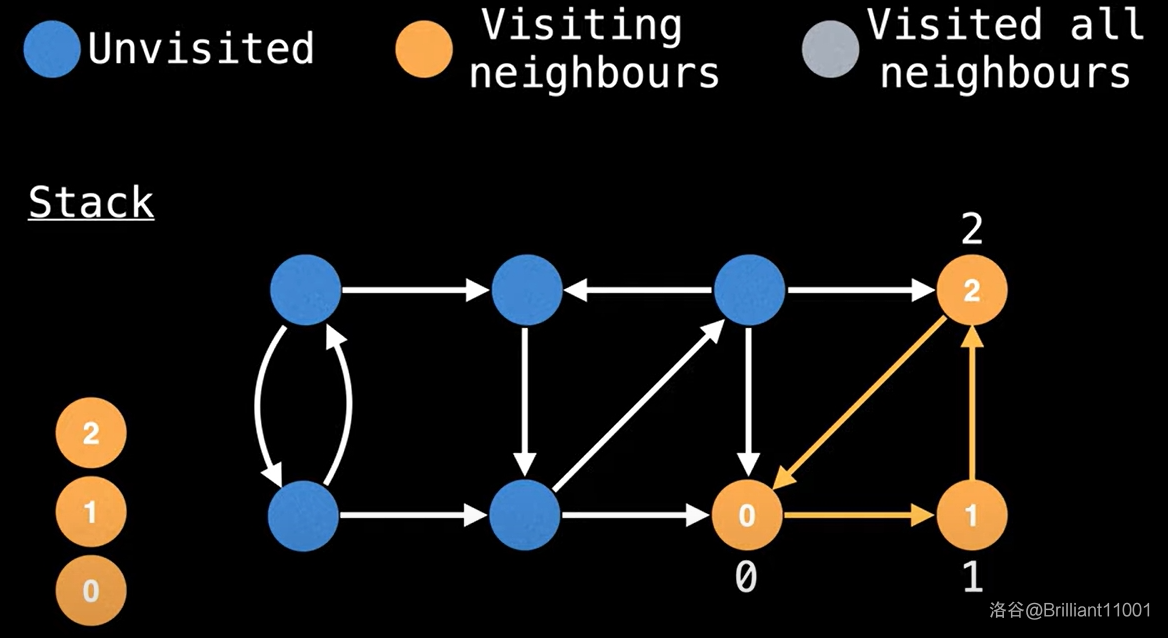
向下搜索,直到无路可走,开始回溯。
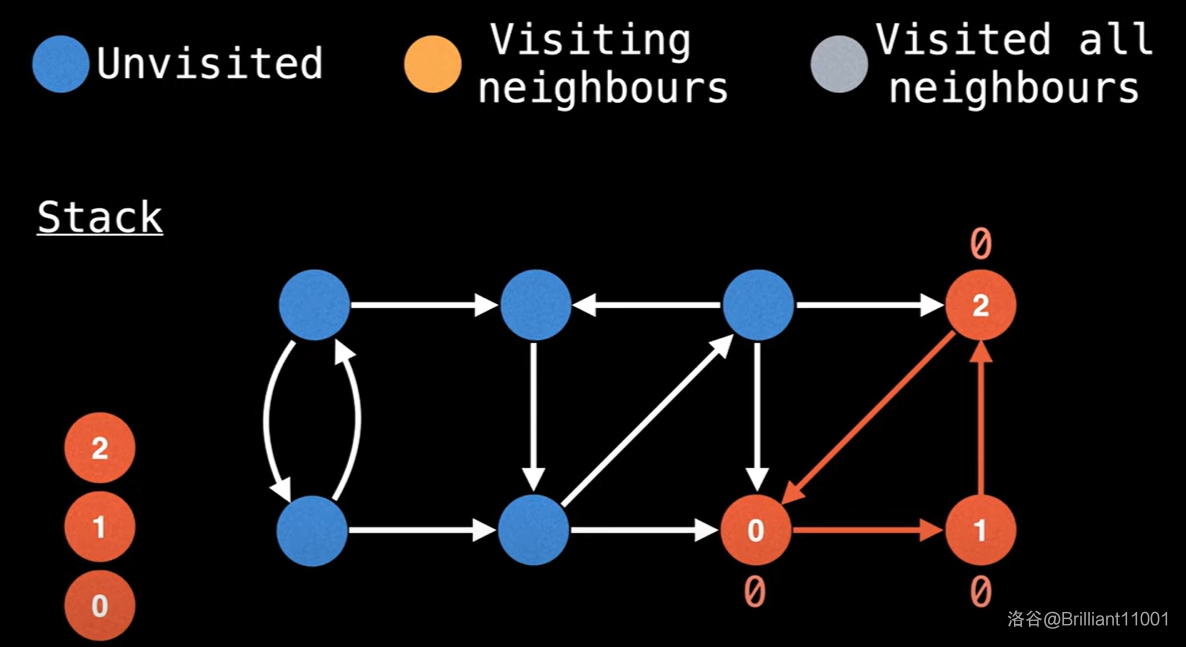
先更新 \(low[2] = min(low[2], low[0]) = 0\)。
再更新 \(low[1] = min(low[1], low[2]) = 0\)。
再更新 \(low[0] = min(low[0], low[1]) = 0\)。
发现 \(low[0] = dfn[0]\),所以将 \(0\) 到栈顶全部弹出,\(\{0,1,2\}\) 构成一个 SCC。
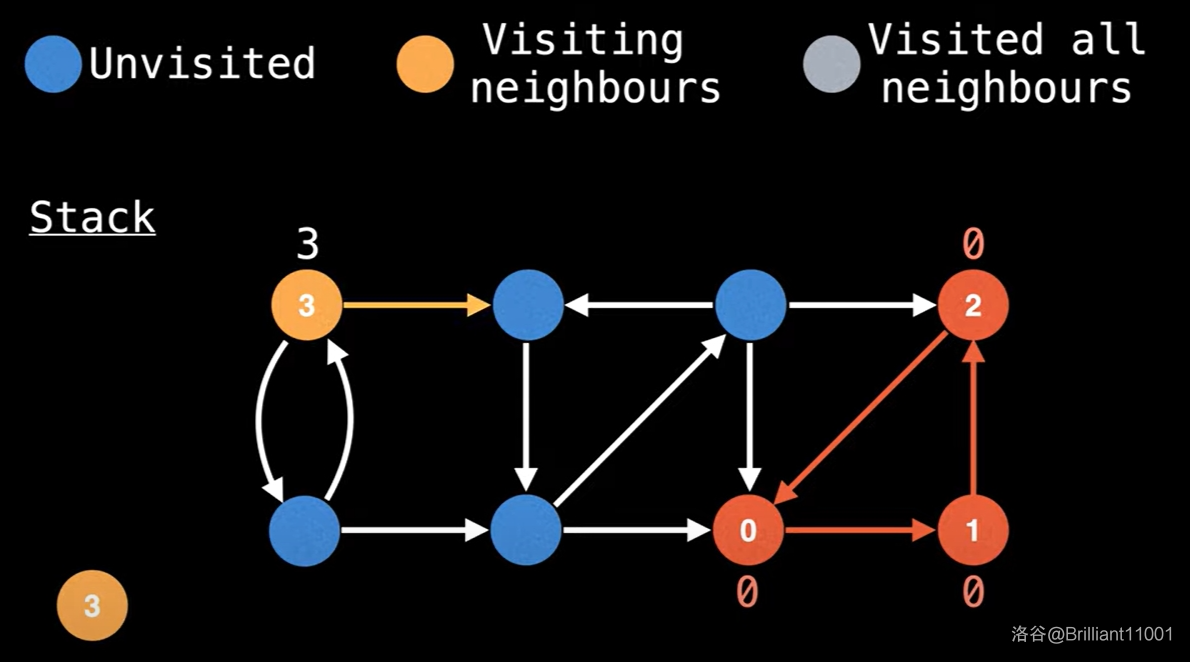
然后从 \(3\) 号点重新开始 dfs。
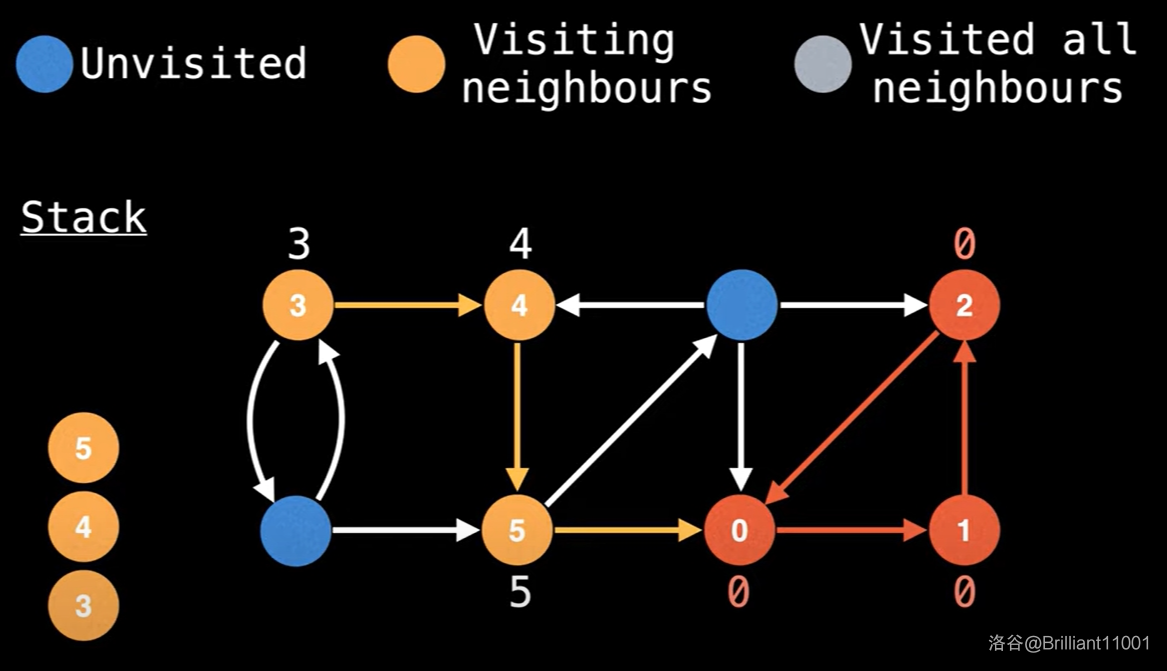
当搜到节点 \(5\) 时,发现 \(5\) 有一条出边连向 \(0\),但 \(0\) 已经访问过且不在栈中,所以不能用 \(0\) 来更新,跳过。
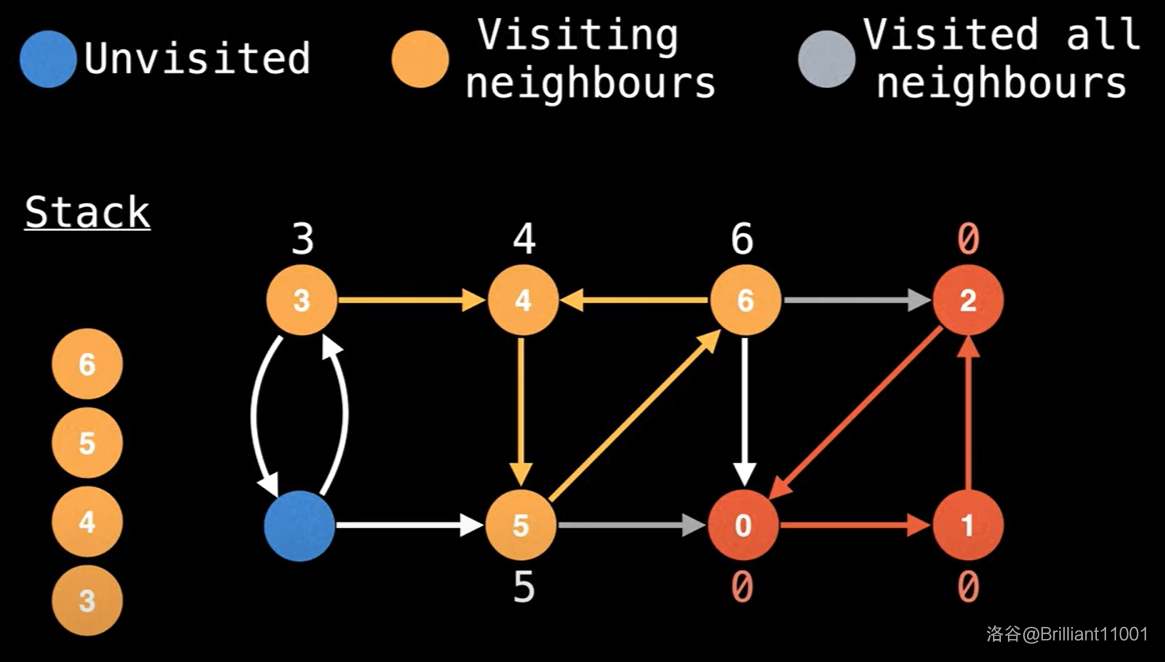
搜到 \(6\) 时也是同理,不能用 \(0\) 和 \(2\) 来更新。但当发现一条出边指向 \(4\) 时,发现 \(4\) 在栈中,所以可以更新。
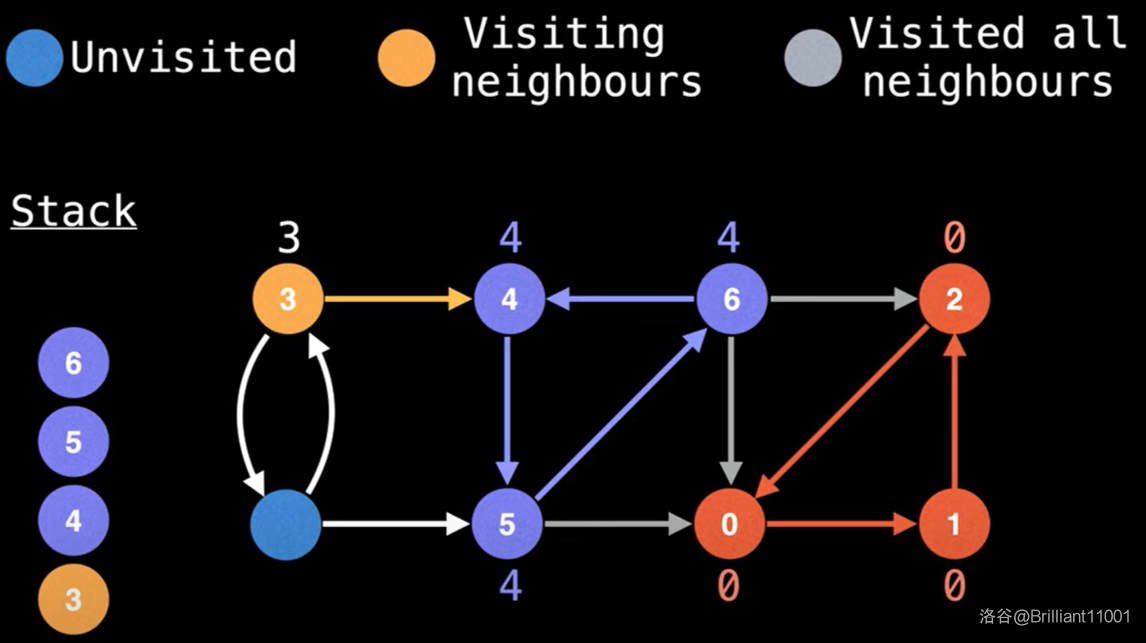
无路可走后,开始回溯。
先更新 \(low[6] = min(low[6], low[4]) = 4\)。
再更新 \(low[5] = min(low[5], low[6]) = 4\)。
再更新 \(low[4] = min(low[4], low[5]) = 4\)。
发现 \(low[4] = dfn[4]\),所以将 \(4\) 到栈顶全部弹出,\(\{4,5,6\}\) 构成一个 SCC。
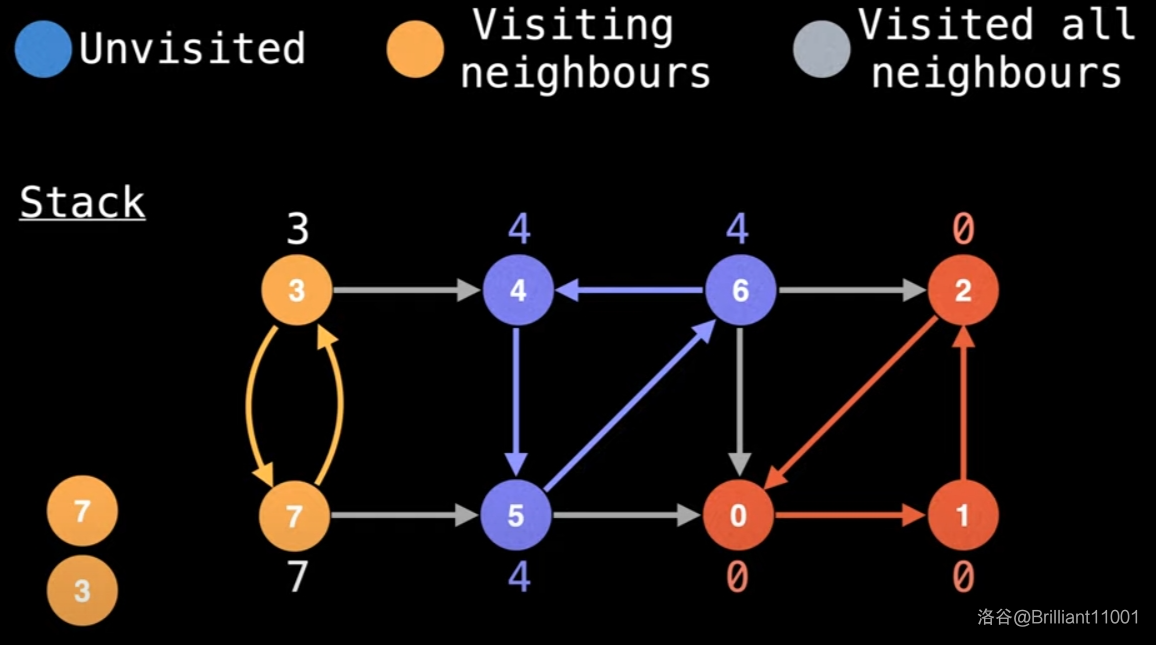
回溯到 \(3\) 后,再遍历点 \(7\)。
然后发现 \(4\) 已经被遍历过且不在栈中,所以不能用来更新,只能回到 \(3\)。
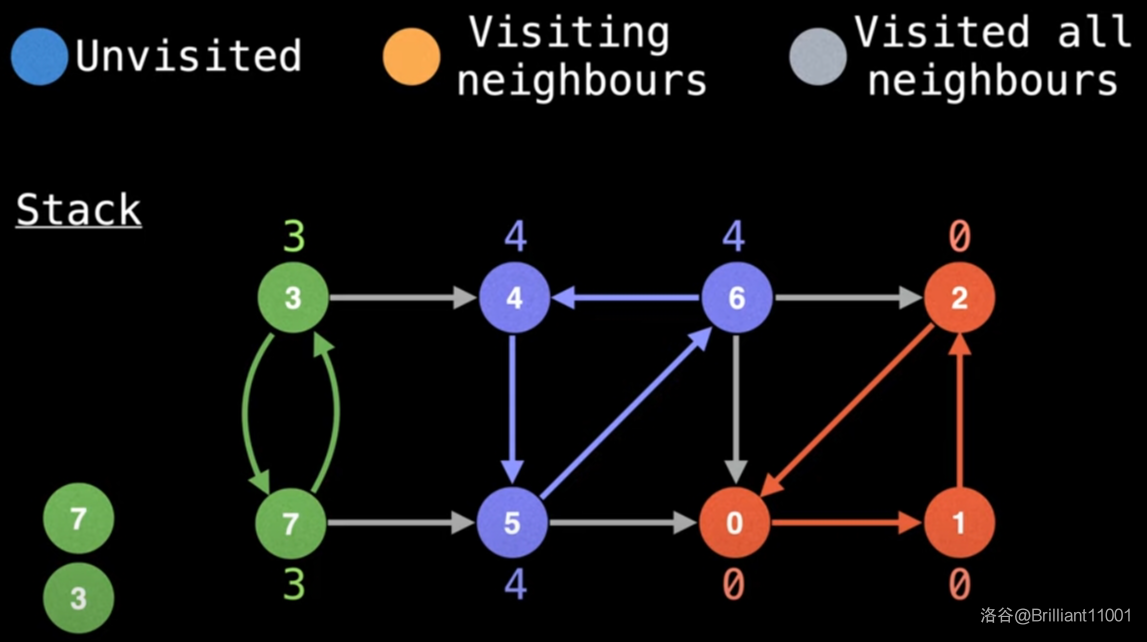
无路可走了,回溯。
先更新 \(low[7] = min(low[7], low[3]) = 3\)。
再更新 \(low[3] = min(low[3], low[7]) = 3\)。
发现 \(low[3] = dfn[3]\),所以将 \(3\) 到栈顶全部弹出,\(\{3,7\}\) 构成一个 SCC。
至此,已找出原有向图的 \(3\) 个 SCC。
根据以上思路可以写出 tarjan 模板:
\(\texttt{Code:}\)
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
stk[++top] = u, st[u] = true;
for(int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if(!dfn[j]) {
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if(st[j]) low[u] = min(low[u], dfn[j]); //这里写成 low[j] 也是正确的,但为了方便和双连通分量的联合记忆,故写成 dfn[j](其实这样写也是对的
}
if(dfn[u] == low[u]) {
int y;
scc_cnt++;
do {
y = stk[top--], st[y] = false;
id[y] = scc_cnt;
}while(y != u);
}
}
特别注意:tarjan 求 SCC 中的 low 数组与求 DCC 的 low 数组定义不同。
前者是:在搜索树中 \(\texttt{subtree(x)}\) 中的所有节点与【经过不在搜索树的边】,能够到达 \(\texttt{subtree(x)}\) 的节点中的最小 dfn。
意思是可以走多步到 \(\texttt{subtree(x)}\) 的点都算数。
后者是:在搜索树中 \(\texttt{subtree(x)}\) 中的所有节点与【经过 \(1\) 条不在搜索树的边】,能够到达 \(\texttt{subtree(x)}\) 的节点中的最小 dfn。
意思是只能走一步到 \(\texttt{subtree(x)}\) 的点才算数。
至于为什么,请参考 Tarjan 论文。(因为我确实不会证)
\(\texttt{0x02}\) 一些例题
题目大意:
给定一张有向图,每个点都有一个权值,求一条路径,使其得到的权值和最大,可多次经过一个点,但只算一次权值。
思路:
因为点权都是非负的,所以我们要尽可能经过尽量多的点,秉承着“既来之,则安之”的观点,我们每到一个点,便一定可以把它所在的 SCC 中的点都给走一遍。所以我们先缩点,在得到的 DAG 上跑最长路即可。
#include <vector>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 10010, M = 200010;
int n, m;
int h[N], e[M], ne[M], idx;
int v[N];
int hc[N], ec[M], w[M], nec[M], idxc;
int stk[N], q[M << 5];
int top, hh, tt = -1;
int dfn[N], low[N];
bool st[N];
int tim, scc_cnt;
int id[N], scc_w[N];
int in_deg[N], out_deg[N];
int dist[N];
vector<int> scc[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void addc(int a, int b, int c) {
ec[idxc] = b, w[idxc] = c, nec[idxc] = hc[a], hc[a] = idxc++;
}
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
stk[++top] = u, st[u] = true;
for(int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if(!dfn[j]) {
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if(st[j]) low[u] = min(low[u], low[j]);
}
if(dfn[u] == low[u]) {
int y;
++scc_cnt;
do {
y = stk[top--], st[y] = false;
id[y] = scc_cnt;
scc_w[scc_cnt] += v[y];
scc[scc_cnt].push_back(y);
}while(y != u);
}
}
int main() {
memset(h, -1, sizeof h);
memset(hc, -1, sizeof hc);
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &v[i]);
int a, b;
for(int i = 1; i <= m; i++) {
scanf("%d%d", &a, &b);
add(a, b);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
for(int i = 1; i <= n; i++) {
for(int j = h[i]; ~j; j = ne[j]) {
int y = e[j];
if(id[i] != id[y]) {
addc(id[i], id[y], scc_w[id[y]]);
++in_deg[id[y]];
++out_deg[id[i]];
}
}
}
int ans = 0;
for(int i = 1; i <= scc_cnt; i++) {
if(!in_deg[i])
q[++tt] = i;
dist[i] = scc_w[i];
}
while(hh <= tt) {
int t = q[hh++];
for(int i = hc[t]; ~i; i = nec[i]) {
int j = ec[i];
dist[j] = max(dist[j], dist[t] + w[i]);
in_deg[j]--;
if(!in_deg[j]) q[++tt] = j;
}
}
for(int i = 1; i <= scc_cnt; i++)
if(!out_deg[i]) ans = max(ans, dist[i]);
printf("%d\n", ans);
return 0;
}
P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G
题目大意:
给定一张有向图,问有多少个所有点都能到达的点?
思路:
根据 SCC 的定义可知:在一个 SCC 内所有点都是互相可达的,所以不妨先缩点,然后整张图就变成了一个 DAG,若这个 DAG 中出度为 \(0\) 的点只有一个,说明存在所有点都能到的点,数量就是那个 SCC 中点的个数,否则不存在。
\(\texttt{Code:}\)
#include <cstring>
#include <iostream>
using namespace std;
const int N = 10010, M = 50010;
int n, m;
int h[N], e[M], ne[M], idx;
int hc[N], ec[N], nec[N], idxc;
int stk[N];
int tt;
int dfn[N], low[N];
bool st[N];
int tim, scc_cnt;
int id[N], scc_siz[N];
int deg[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
stk[++tt] = u, st[u] = true;
for(int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if(!dfn[j]) {
tarjan(j);
low[u] = min(low[u], low[j]);
}
else if(st[j]) low[u] = min(low[u], dfn[j]);
}
if(dfn[u] == low[u]) {
int y;
++scc_cnt;
do {
y = stk[tt--], st[y] = false;
id[y] = scc_cnt;
++scc_siz[scc_cnt];
}while(y != u);
}
}
int main() {
memset(h, -1, sizeof h);
memset(hc, -1, sizeof hc);
scanf("%d%d", &n, &m);
int a, b;
for(int i = 1; i <= m; i++) {
scanf("%d%d", &a, &b);
add(a, b);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);
for(int i = 1; i <= n; i++) {
for(int j = h[i]; ~j; j = ne[j]) {
int y = e[j];
if(id[i] != id[y]) deg[id[i]]++;
}
}
int ans = 0, cnt = 0;
for(int i = 1; i <= scc_cnt; i++)
if(!deg[i]) cnt++, ans += scc_siz[i];
if(cnt == 1) printf("%d\n", ans);
else puts("0");
return 0;
}