mpc

标签：SPDZ MPC 同态 SS 算法 计算 mpc

https://blog.csdn.net/apr15/article/details/133965768

 

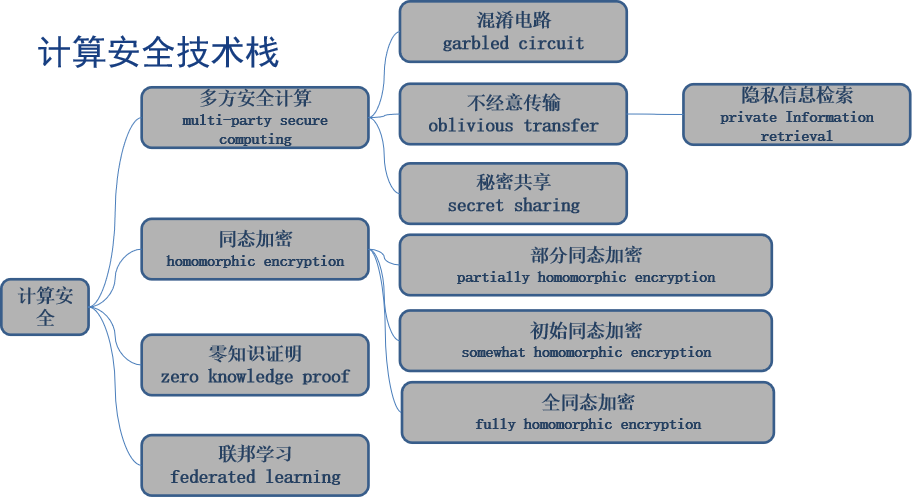
在“数据安全概述”里面， 我们提到了安全多方计算SMPC（Secure multi-party computation）的技术。在这个计算里面代表是密码分享SS （secret sharing）技术。 

 

 

而开启整个算法世界的其实是华人科学家姚期智教授， 他提出了百万富翁问题， 一下子引发了全世界密码学专家的思考，4年后他还提出了混淆电路解决了这个问题。 

 

至此电路的思想已经深入人心， GMW就是利用了电路+SS+OT的思想，但是抛弃来的混淆，而采用了随机尾数的方式。

 

到了BGW，进一步加速了

 

 

而这一切的基础是RSA （Rivest, Shamir, Adelman）非对称加密算法的发明。

 

 

 

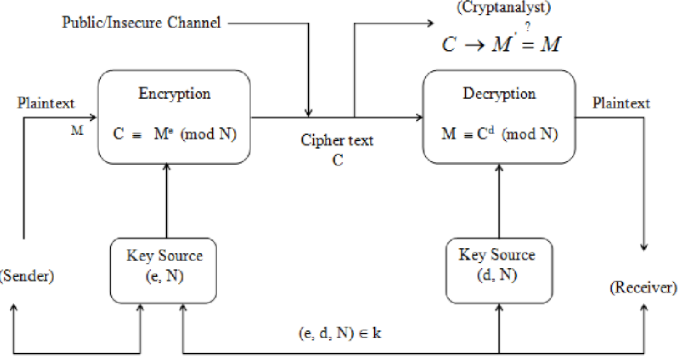
在RSA的基础上，诞生了OT （oblivious transfer）算法， 实现了N选1的双方隐私保护。 

 

 

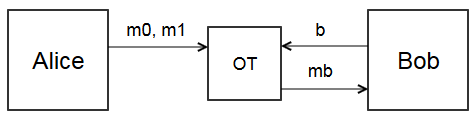
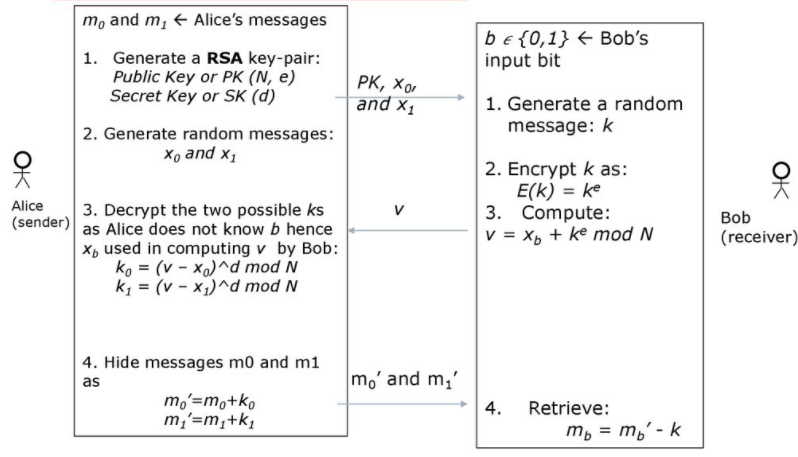
OT通过利用RSA，通过引入3个随机数（x0, x1, k) 然后通过加密后实现对选择序号的保密，以及对原始2个带选择数的保密。 同时通过两次对同一个序号进行反向处理，实现只有对应，序号的数能够被恢复。 

 

 

上述发明成为开启整个多方安全计算时代的雷声。

 

前言

 

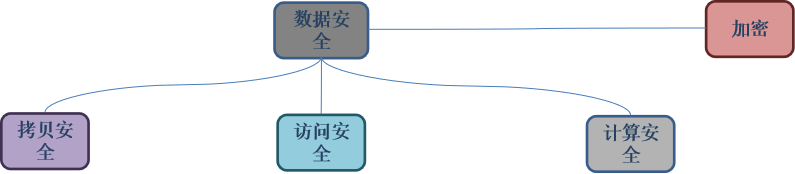
数据安全越来越重要了，为了确保数据安全， 常见的技术手段有拷贝安全， 访问安全， 计算安全，当然这些方面都离不开加密技术。因而，密码学的人的春天来了。 

 

 

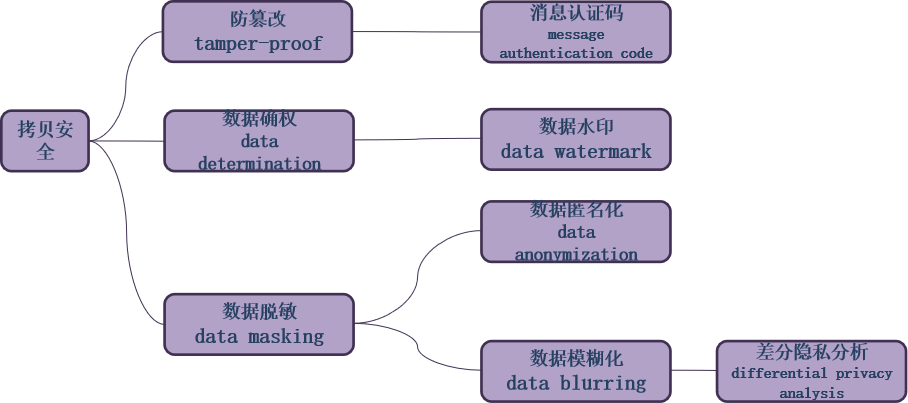
拷贝安全常见的方法有防篡改， 数据确权， 数据脱敏等方法。 

 

 

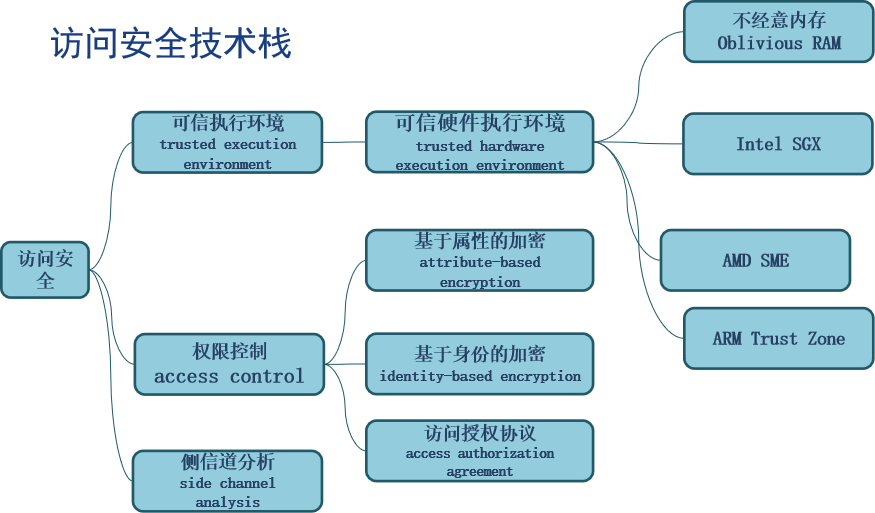
访问安全经常采用可信执行环境， 权限控制等。 

 

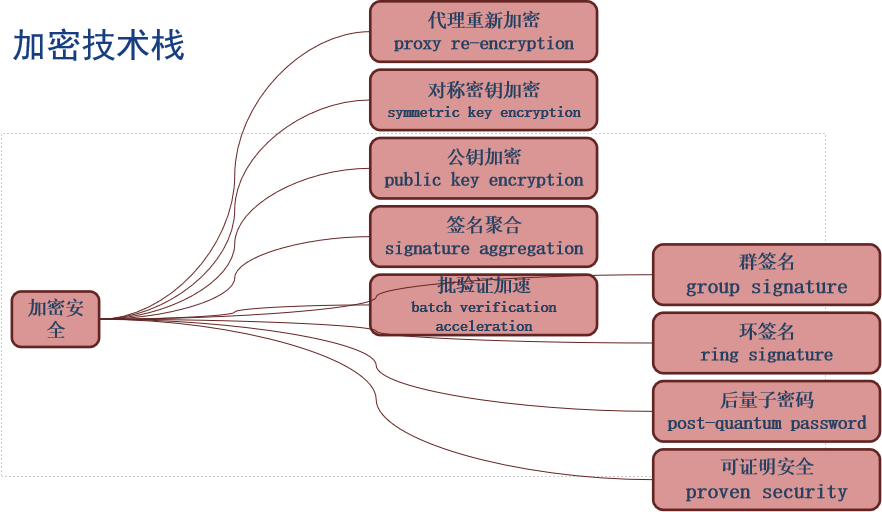
当然目前密码学的进展也日新月异， 尤其后量子密码时代来临。 

 

 

 

多方安全计算 - 起步

 

当存在多方的时候， 最简单的情况是，找一个信任的天使方， 大家把数据给他， 然后进行联合计算。这种情况下， 即便有恶意方， 他也无法看到各方隐私数据。 

 

 

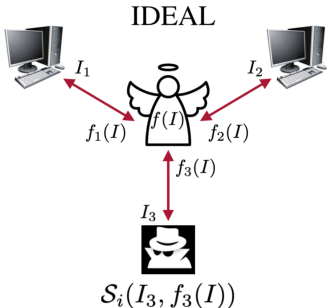
但是，现实场景中， 这个天使方往往是不存在的。这种情况下， SS技术提出， 将数据切分多份， 然后分布到不同的计算节点上进行计算， 每个计算节点都无法还原原始数据， 但是可以推进计算结果，最终多个计算节点的结果进行整合就得到了最终结果。 

 

 

 

 

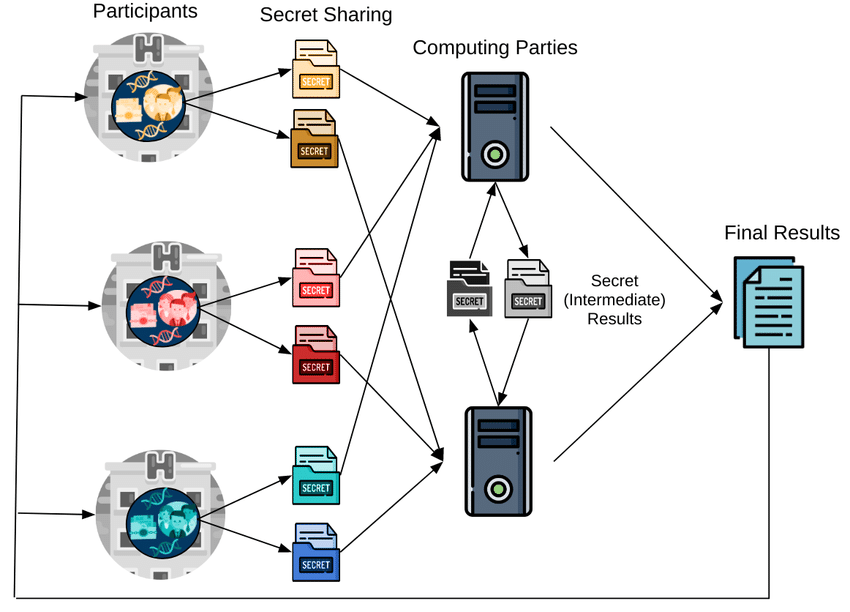
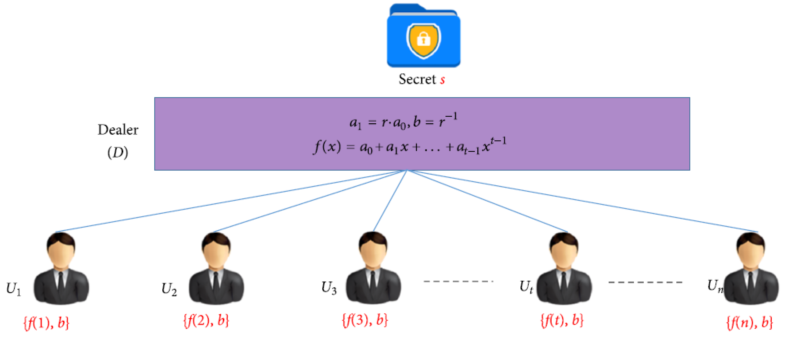
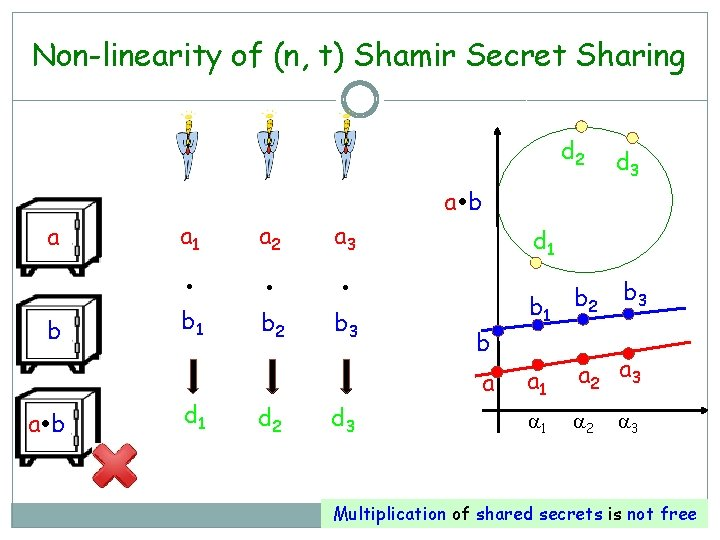
Shamir算法

 

这个Shamir就是著名的RSA算法的S， Adi Shamir。 

 

早期Shamir提出了多项式原始的SS技术，通过拉格朗日差值法，实现秘密通过多项式方程的参数分享到多方，实现既不分享原始内容，也不分享原始内容的加密形态，而且具有可解方式的组合个数就可以破解的能力。 

 

 

 

 

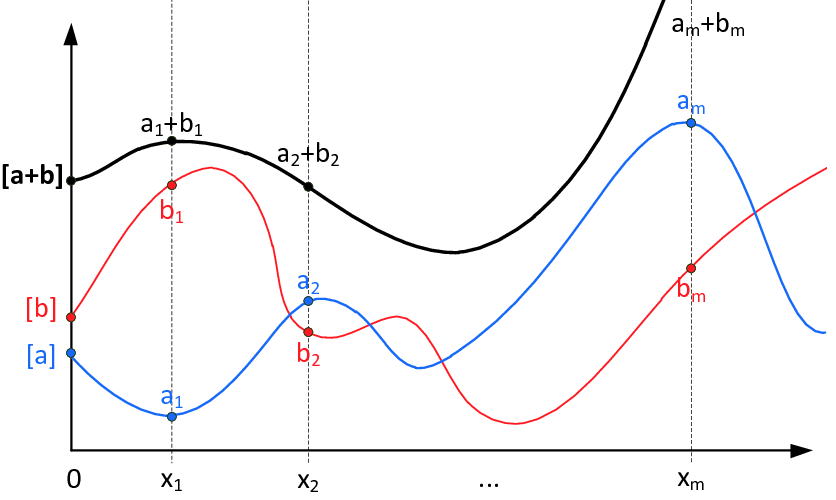
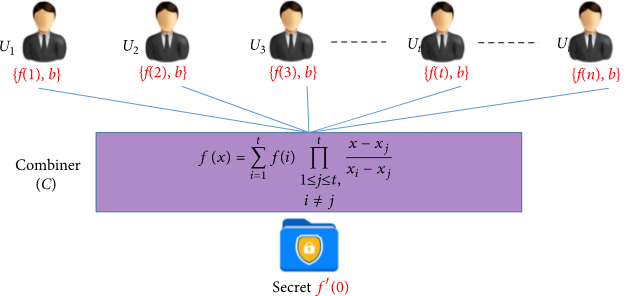
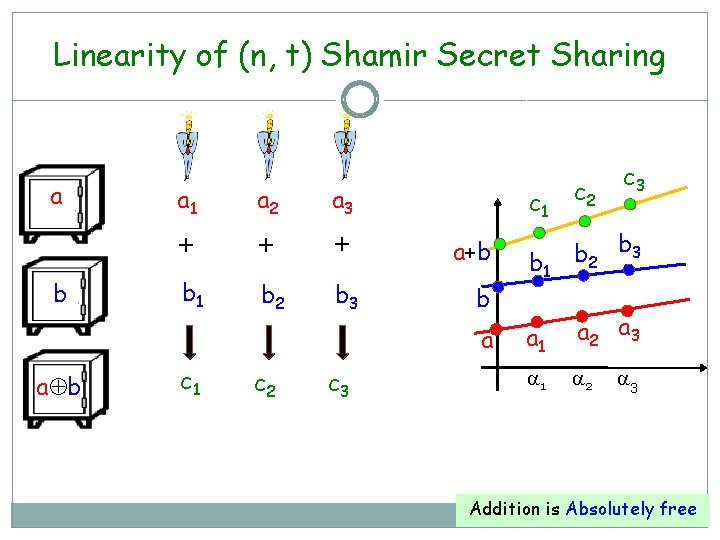
这种技术对加减法非常友好。

 

但是对于乘法来说， 计算非常复杂， 通信量非常大。 

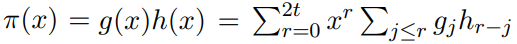
并且如果全部计算的话， 选择数维度就变成了2t。当然可以通过只保留低阶的值进行截断计算，来还原 。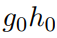

 

 

 

 

 

GMW算法

不久GMW就提出了改进算法，希望通过GC的方法来实现乘法部分，提高效率。 

 

或许受到了姚期智教授的混淆电路的想法的触发， GMW提出了基于布尔电路来实现，尤其对于其中的乘法。 

 

 

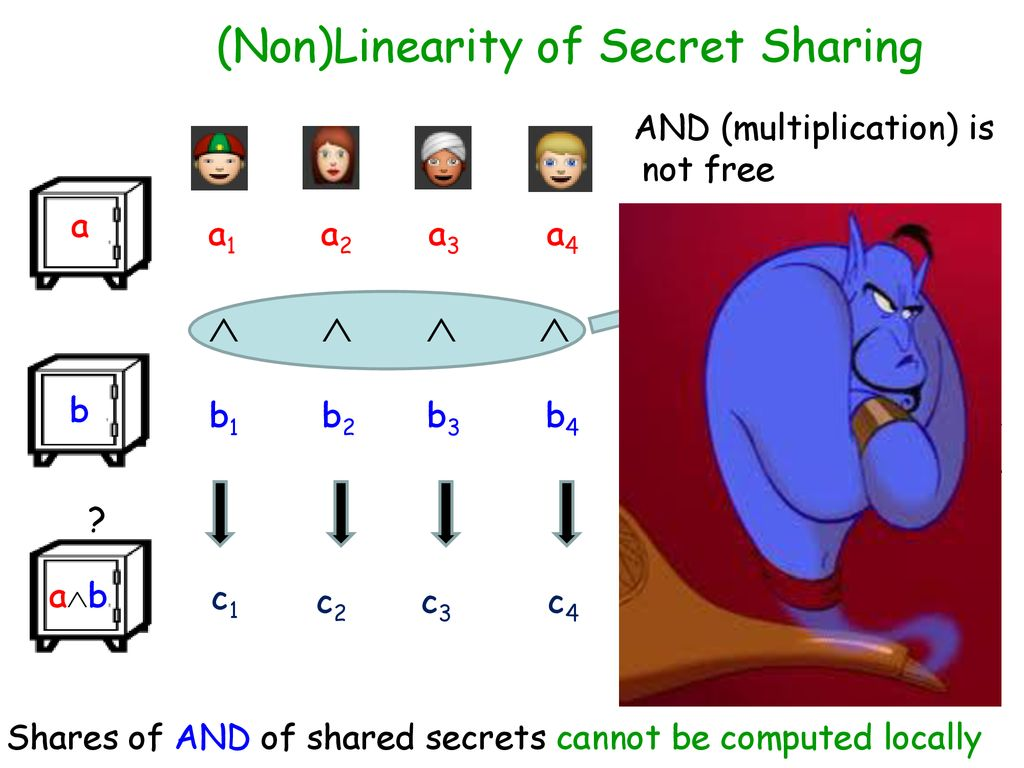
跟进布尔电路， 那么要隐藏b的一方信息，就可以通过OT方法来实现。 

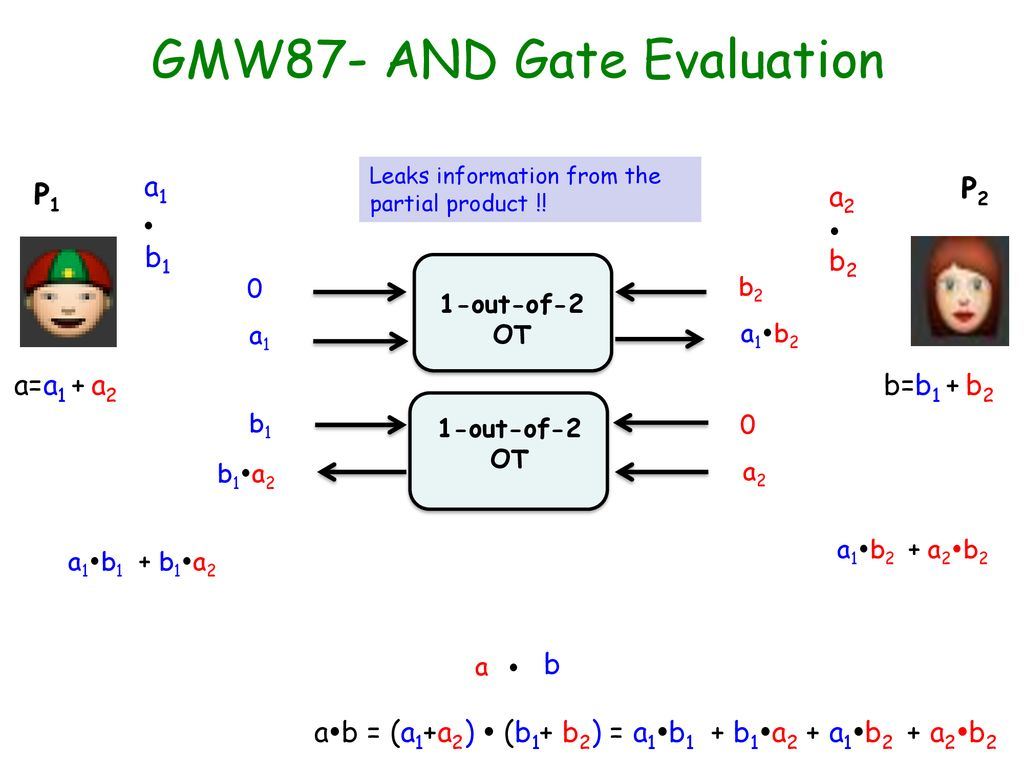
但是还是没有隐藏a的信息， 那么再通过加一个随机数来隐藏a。 

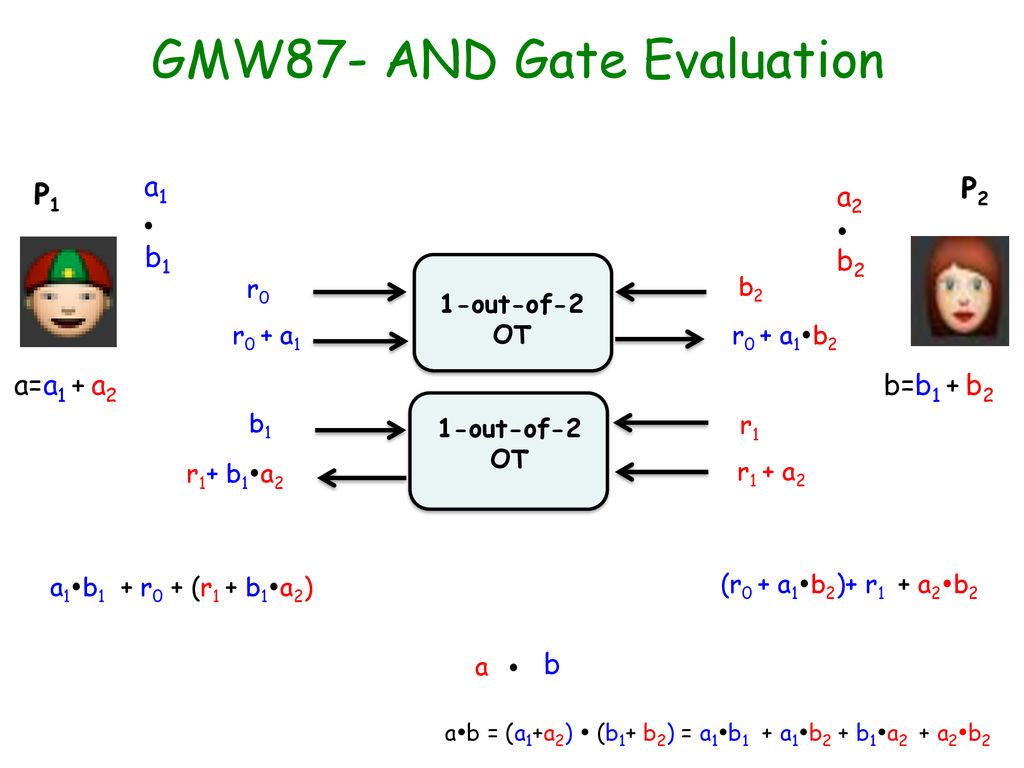
而添加了r0,r1后， 乘积里面的r0+r1是很容易通过SS实现的。因此解决了乘法问题。 

 

BGW算法

是 BenOr-Goldwasser-Wigderson 三位大神，在一起搞的算法。 

 

BGW里面直接应用算数电路，化简了多方计算来划分加法乘法。 

 

然后再通维度约减后的Shamir的SS算法实现乘法运算。

 

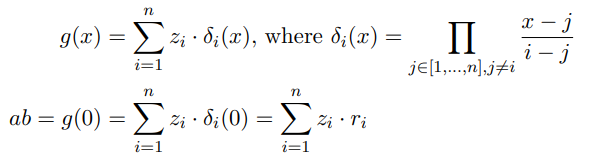
所以， 总得来说GMW是既支持bool电路，也支持算数电路。 但是BGW是基于SS的，仅仅支持算数电路。 

 

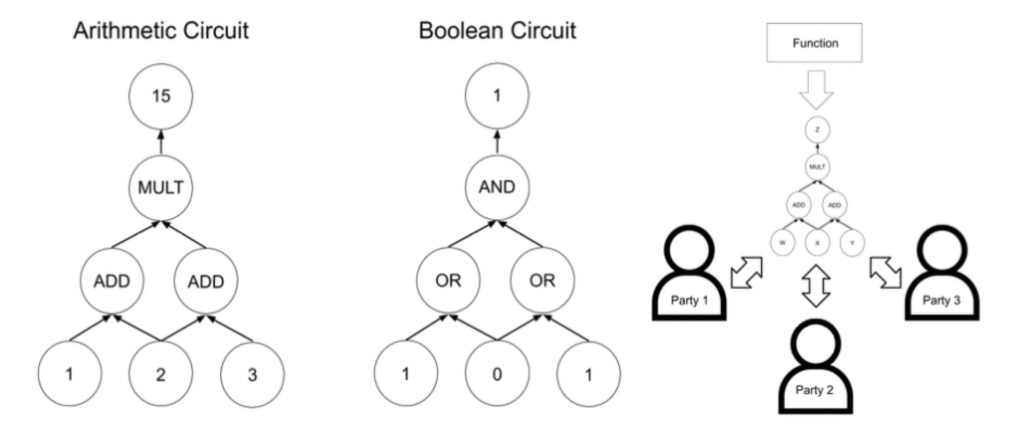
Active Passive 安全模式

 

类似的电路的的情况，可以看到FairMP， Sharemind等等。 

 

 

其中security一般可以分为3种大的类型：

1.  Semi-honest 半可信， 一般也叫Passive模式。

2.  Malicious 恶意， 一般也叫Active 模式。 

3. 还有一种介于2者间， Covert 间谍， 

对于GMW，或者BGW，要实现Active模式， 可以使用Reed-Solomon Encoding，对错误的部分进行校验并恢复。 

 

李德所罗门编码 Reed-Solomon encoding

 

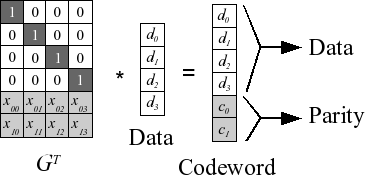
如果支持Malicious状态， 那么就可以称为是Verifiable Secret Sharing VSS了。 

 

 

 

多方安全计算 - 高速发展

 

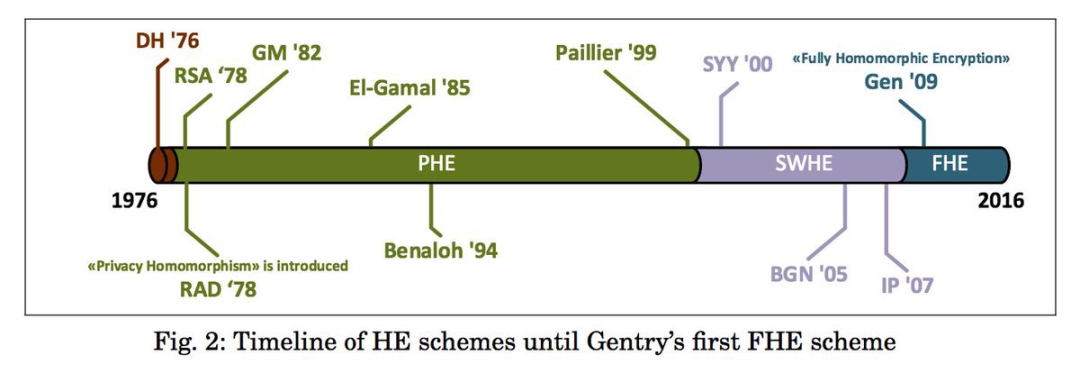
跑过早期的概念成熟，就开始追求性能可用了。 而这其中最大的进步在于同态加密发展。 

 

同态加密

 

同态的思想提供了超前的模型， 就是在明文空间的操作， 可以实现密文空间的映射。并且结果还能映射回明文空间。 

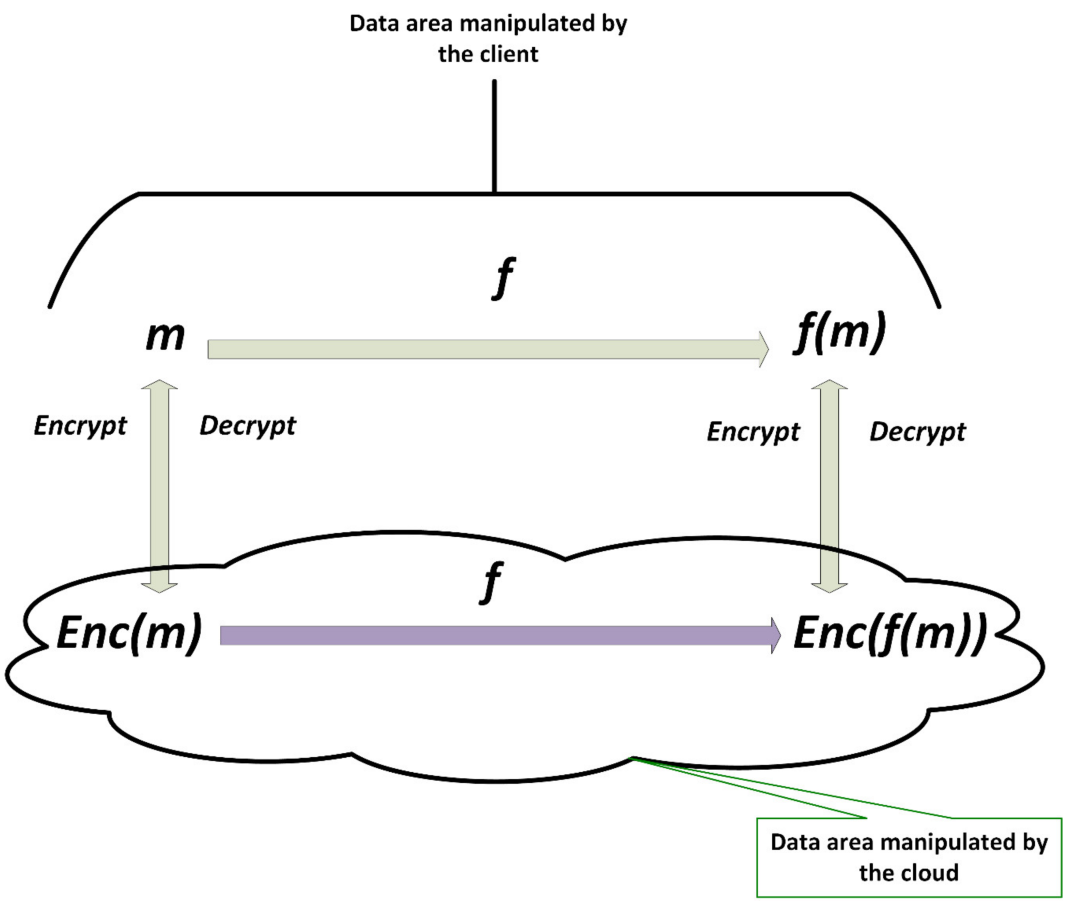
类比一下，就是把加法映射到字符空间的“加法”， 而结果解密之后恰好就是明文空间的结果。 

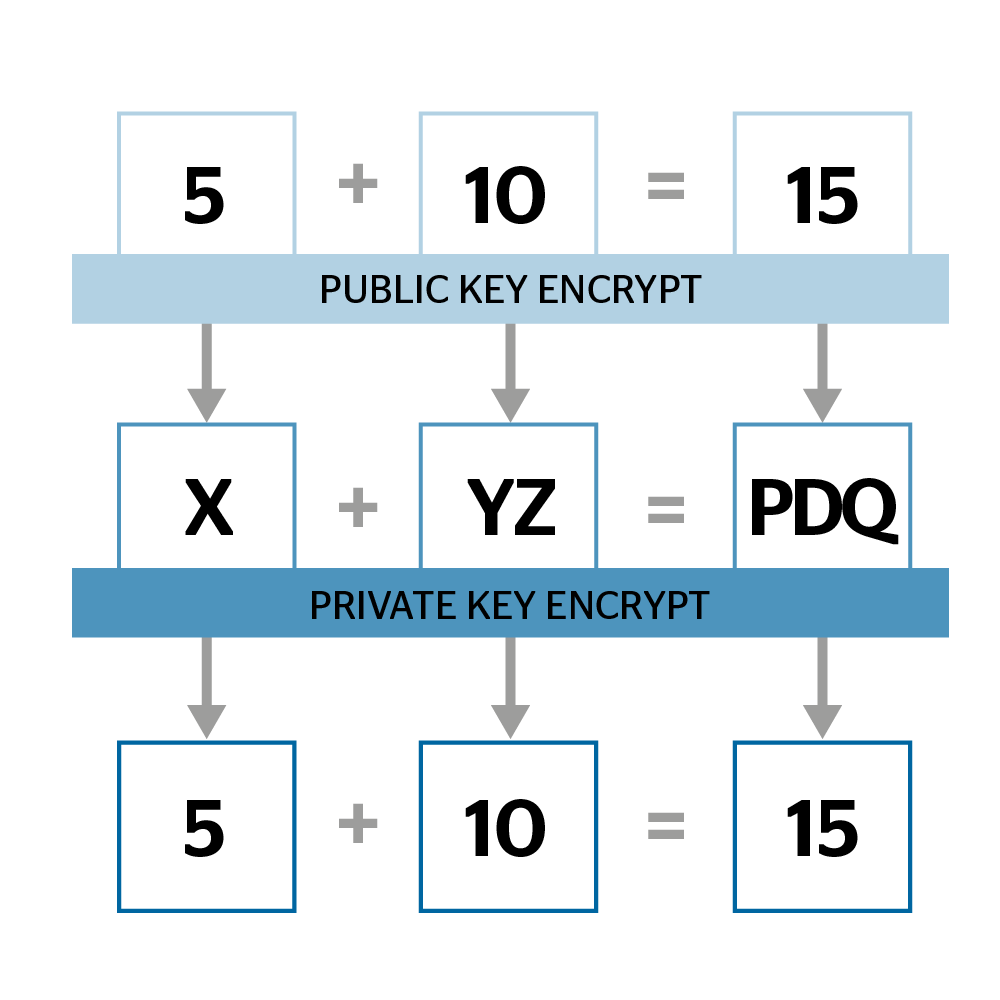
早期， 人们发现加法可以比较容易的实现同态。 

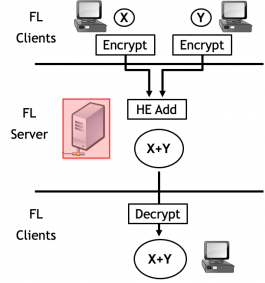
经典的加法同态：

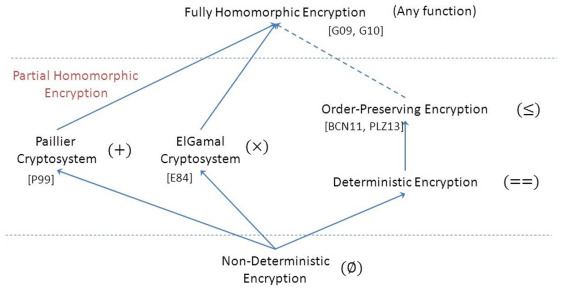
1.  Pailier  算法

经典的乘法同态：

1.  EIGamal  加密算法

2.  RSA 加密算法

同态加密的发展正当时，希望继续涌现非凡的华人领袖解决性能问题。 

 

 

SPDZ 算法

 

有了同态的世界， 通信变得小很多。 经典的秘密分享一般分为数据节点， 计算节点。

 

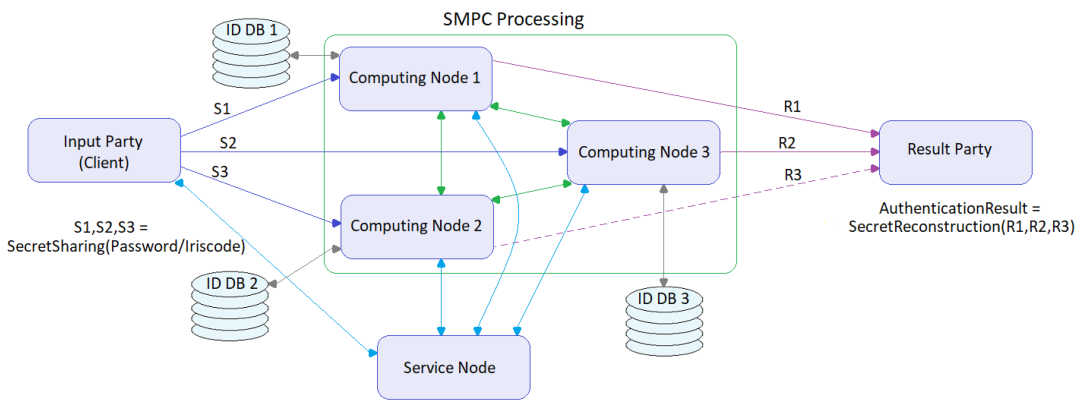
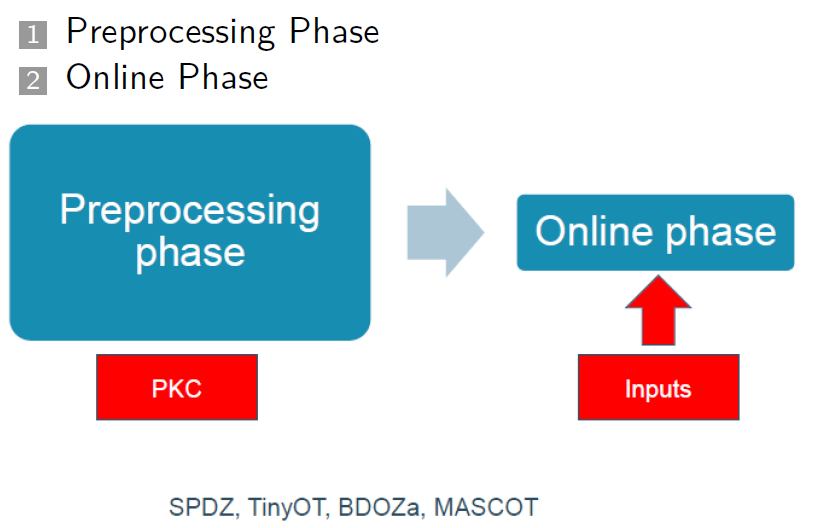
如果深入分析， 提出算法优化， 那么在乘法阶段其实可以做一些优化生成Beaver 三元组， 可以极大的减少运算数目， 但是会带来流程上的变化， 那就是要增加预训练阶段。 

 

Beaver Triples

 

 

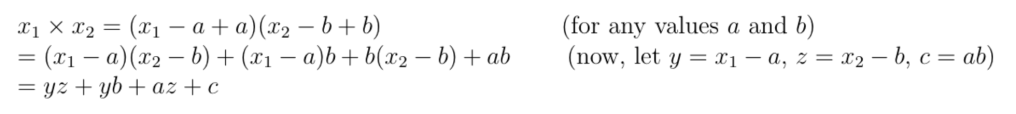
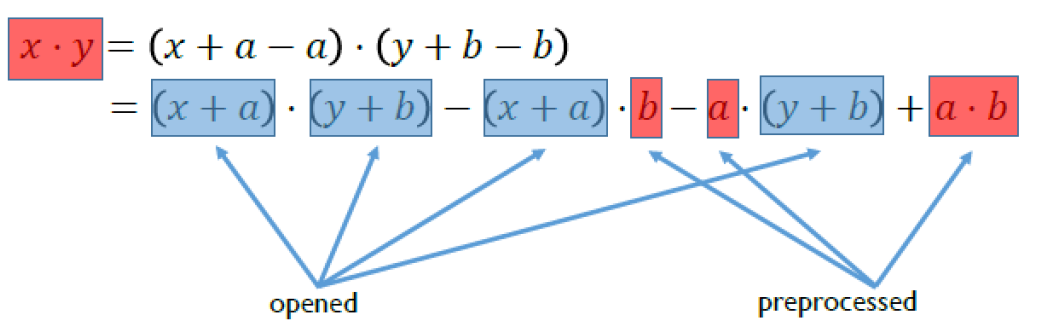
其中的加法与乘法就可以采用SHE进行预处理：

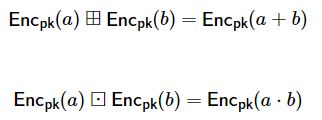
在预处理阶段， 使用了SHE进行计算，极大的加快了计算效率，减少了通信内容。  

 

预训练阶段的差异：

BeDOZa: 最早提出使用SHE来进行预训练处理加法。

SPDZ: 在BeDOZa的SHE思想基础上，处理乘法。

MASCOT: 使用OT算法减少SHE的计算时间，用通信换计算，缩短时间。

Overdrive: 继续回到SHE, 提高计算效率。 

 

对于Malicious Active 的情况下， 需要既保证通信的信息是对的， 也要保障执行了SHE加密（尤其是offline的情况下）。 

 

 

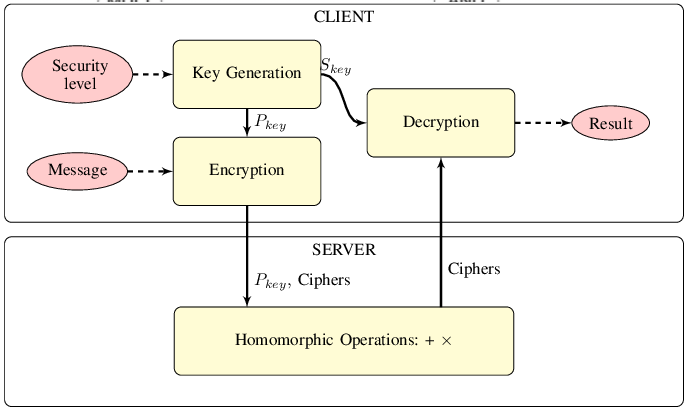
对于通信信息的校验一般采用MAC方法进行确认。 而对于离线情况的确认一般采用ZKP （Zero-Knowledge Proofs）。

 

 

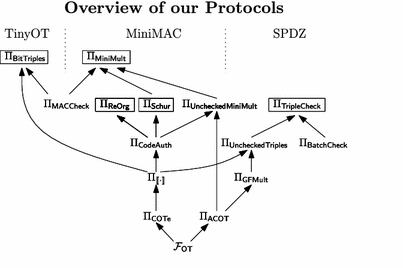
一旦引入了MACs与ZKP，那么整个计算流程就会变得复杂， 等待依赖也会变得复杂， 从工程的角度， 如何并发执行，可以进一步优化等待时间。  

 

SDPZ2 就是类似角度进行的优化:

1）从减少在线计算时间，进行离线数据准备。 

2）MAC的校验与SS部分数据进行重用。

3)  SHE 也优化了BGV实现。

 

工具包混合实现

 

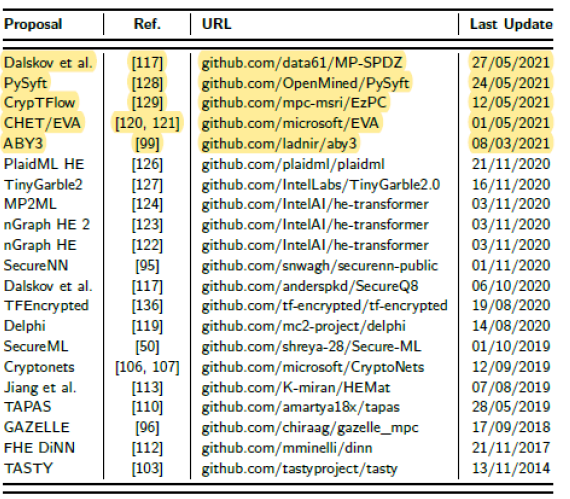
越来越多的多方安全计算的工具包包含不止一种基础算法了。 例如ABY， MPyC，SPDZ的后继（SCALE-MAMBA 与 MP-SPDZ）

 

 

 

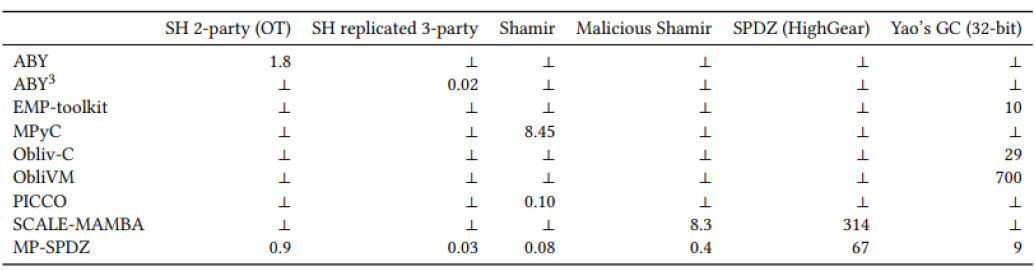
OT， 电路， SS，同态 如何组合已经成为多方安全计算的一门架构学问。 尤其在同态加密突飞猛进的年代里， 更重方案都可能螺旋式的上升， 一会儿被超越， 一会儿又赶超。 

 

 

 

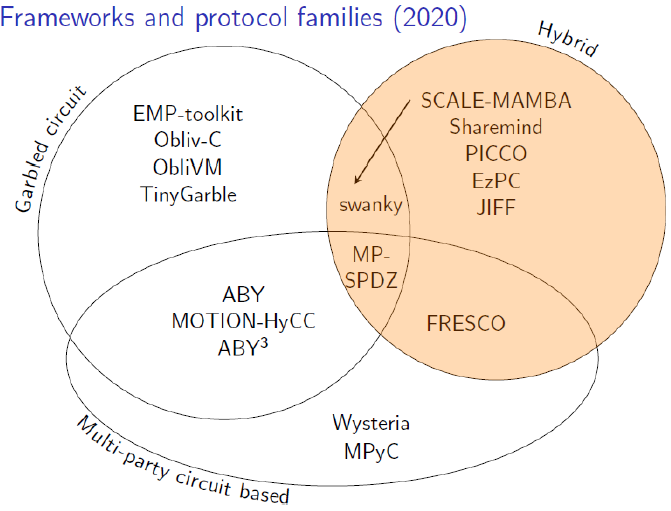
但就目前而言， SPDZ系列还是占据了多方安全计算的主流， 毕竟天下武功，唯Speed不破。 

 

SPDZ系列：

1. SCALE-MAMBA 与 MP-SPDZ：SPDZ的兼容优化

2. Pond协议: SPDZ的优化

 

另外就是基于Shamir + 电路的改进：

1.  MPyC

2.  ABY3

 

 

多方安全计算 - 地基之上

 

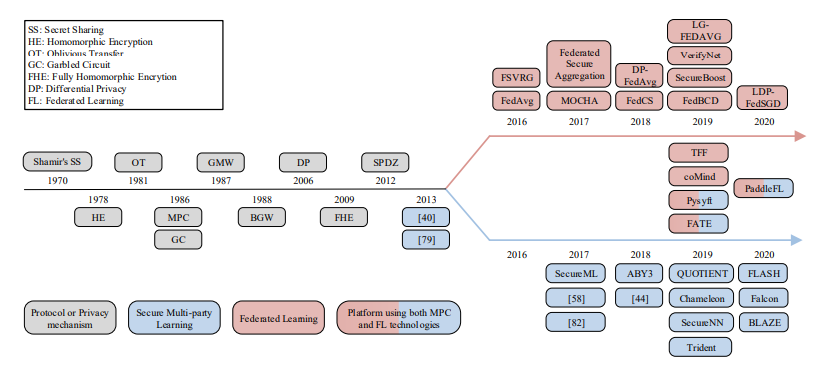
在多方安全计算的地基之上， 现在开源的数据隐私计算平台如沐春风，百花齐放。 其中MPC已经更为各大平台支持的底层能力。 例如：Tensorflow-federated (TFF), TF-encrypted, Paddle FL, PySyft, FATE, CrypTFlow, CrypTen等。 

 

 

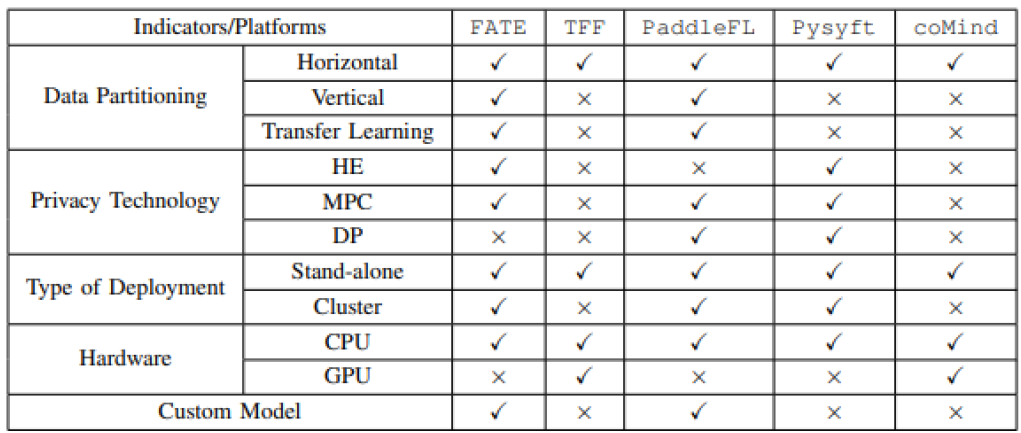
同时，大家也要注意， 最近几年开源的同态加密的库也进入大爆发。 每次同态的大爆发， 后续一定会影响到MPC的开源库的进展。 相信不久MPC基础库还得再有很多进一步的大改进。

 

 

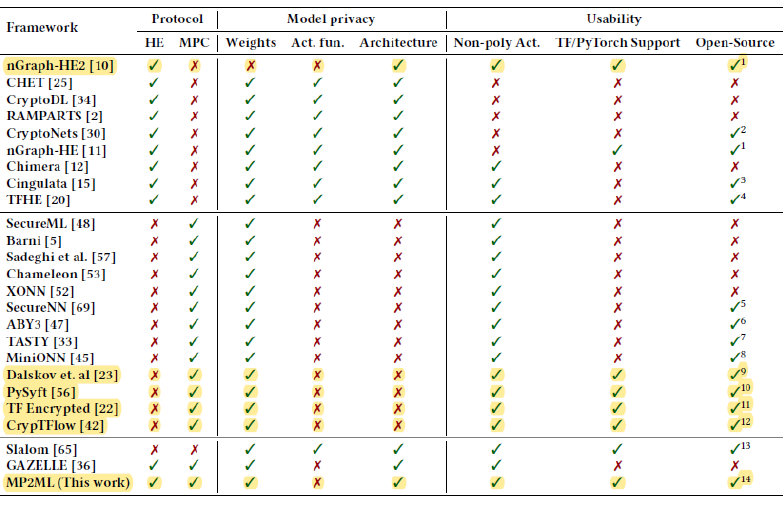
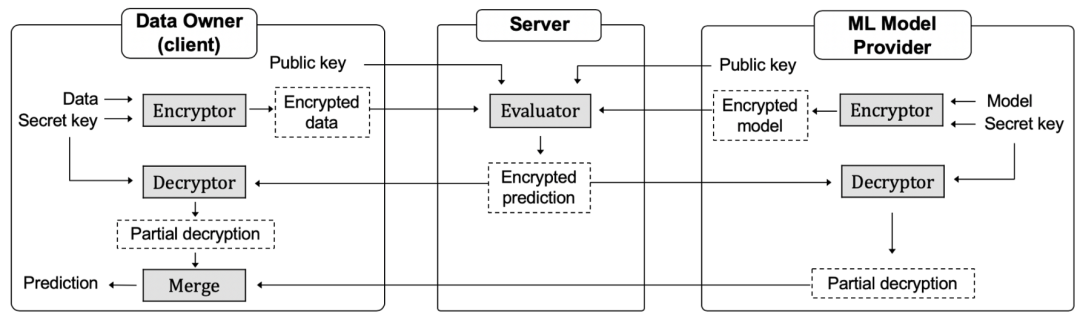
在FATE, PySyft, PaddleFL等上层的数据平台，它们的基础架构非常类似。基本采用加密 + 机器学习分层。 其中加密大部分是C-S架构的。 

 

 

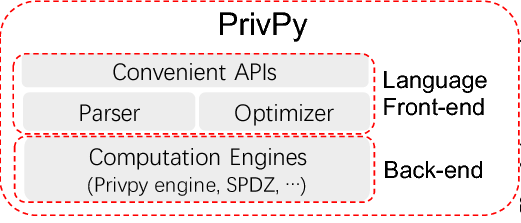
华控清交PrivPy

PrivPy后台也是以SPDZ为主要MPC的方法。 

 

 

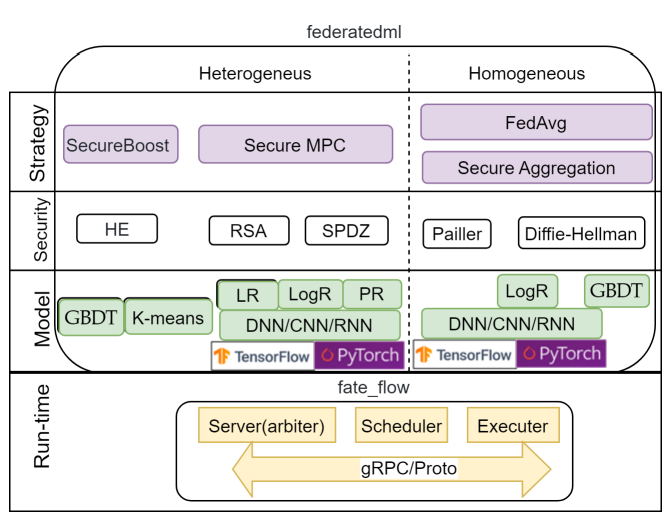
微众银行FATE

FATE后台也是以SPDZ为主要MPC的方法。 

 

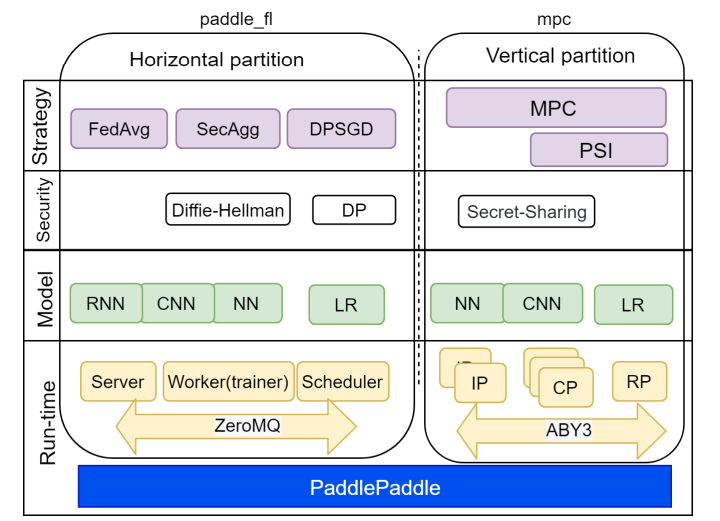
百度PaddleFL

PaddleFL后台也是以ABY3为主要MPC的方法。 

 

 

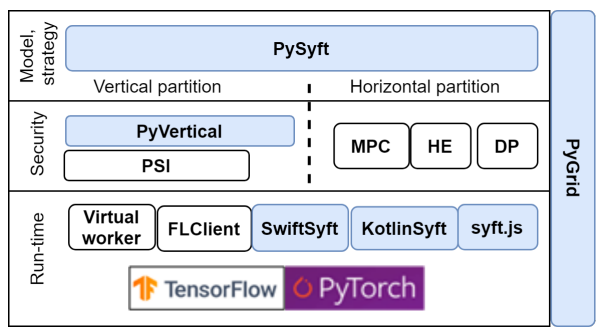
OpenMined的PySyft

PySyft后台也是以SPDZ，SecureNN为主要MPC的方法。

 

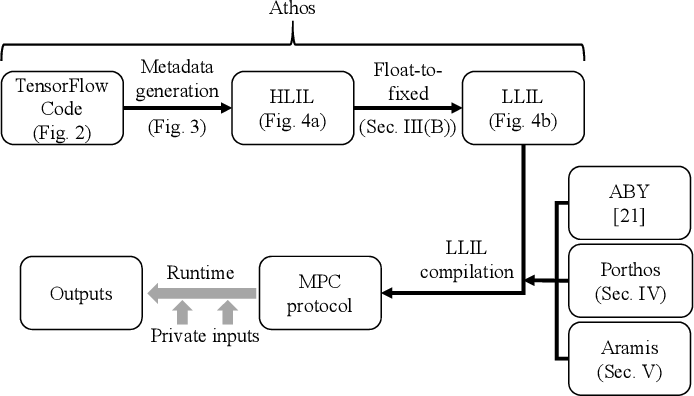
微软的CrypTFlow

CrypTFlow后台也是以EzPC-Aramis为主要MPC的方法，Aramis是GMW + Porthos （SecureNN的定制版）。

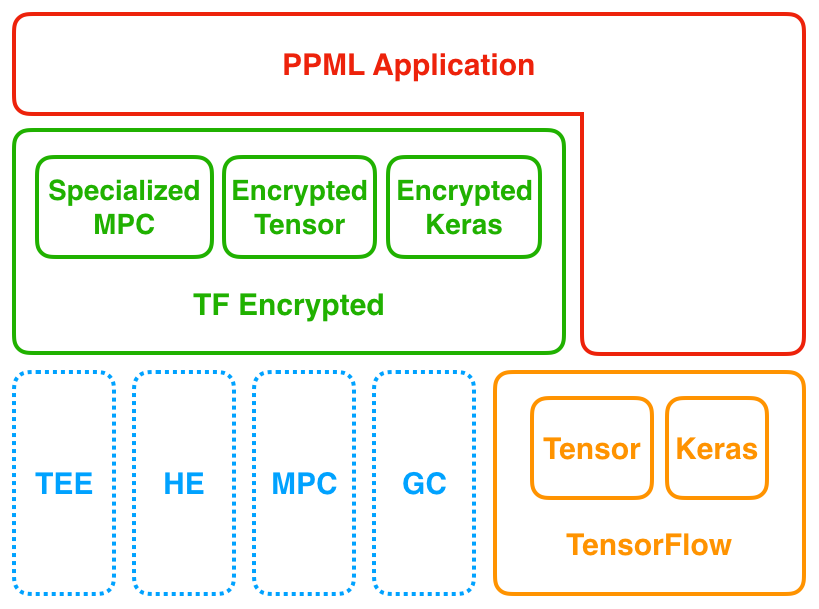
DropoutLabs, Openmined, Alibaba的TF-Encrypted

TF-Encrypted 后台也是以Pond(SPDZ的定制实现)为主要MPC的方法。

 

 

 

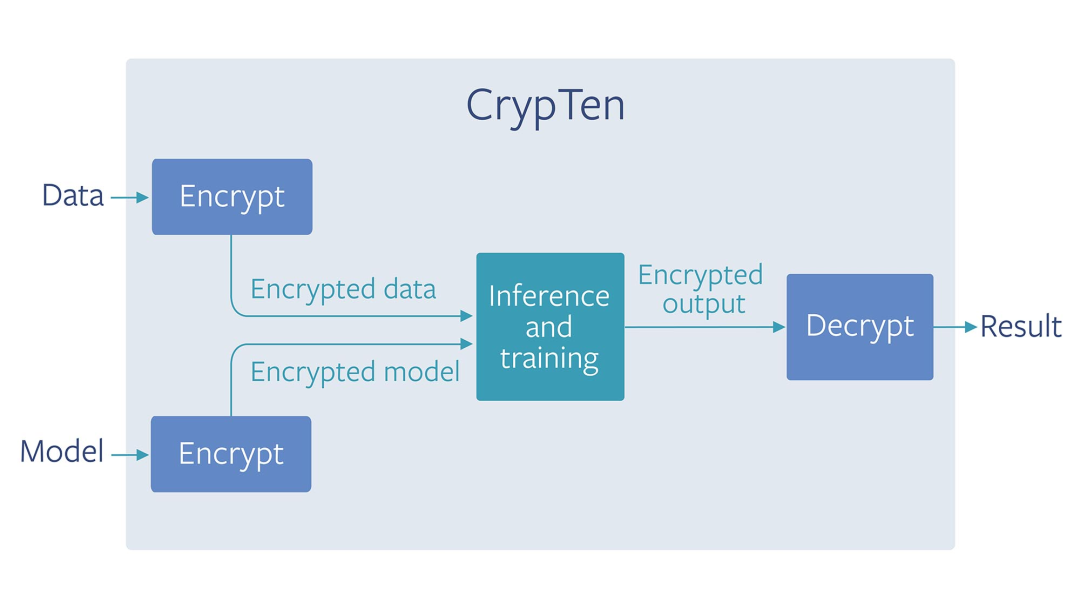
Facebook的CrypTen

CrypTen后台也是以SPDZ为主要MPC的方法。

 

 

思想融合趋势

 

近年， 以SecureNN为代表的机器学习方法， 直接把SS秘密分享的思想进行融合到分布式机器学习中。 在实际实现中以OT为主要参数隐私保护方案。 

 

SecureML, MiniONN, Chameleon, Gazelle, CHET, Delphi 等方法，就是希望把机器学习的原子操作， 例如矩阵乘法， 卷积计算，布尔boolean等使用各种MPC的方法进行安全计算。 

 

 

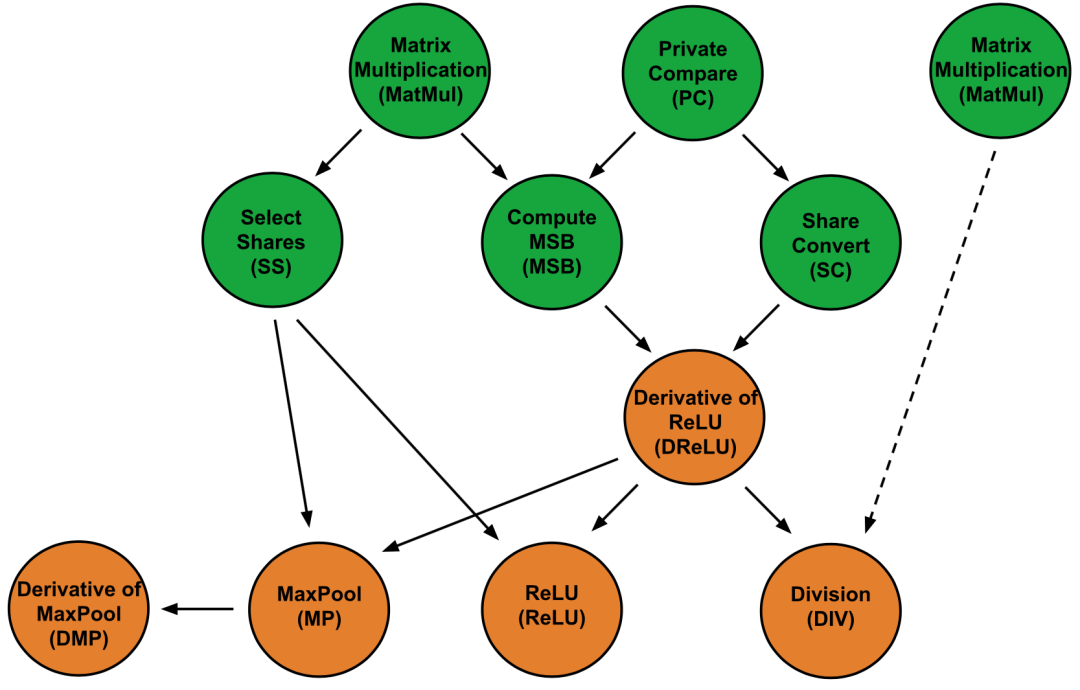
再进一步优化各种非线性的操作，实现基本的非线性函数能力。 

 

 

 

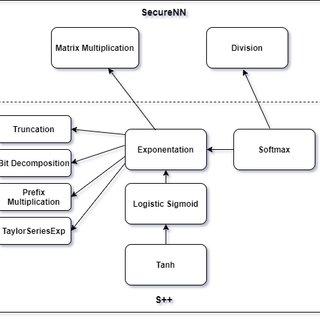
然后可以实现基于这里原子操作的各种神经网络的隐私计算。 

 

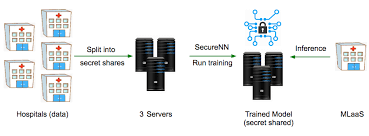
可见从2方，到3方， 再到4方的平台越来越多。

 

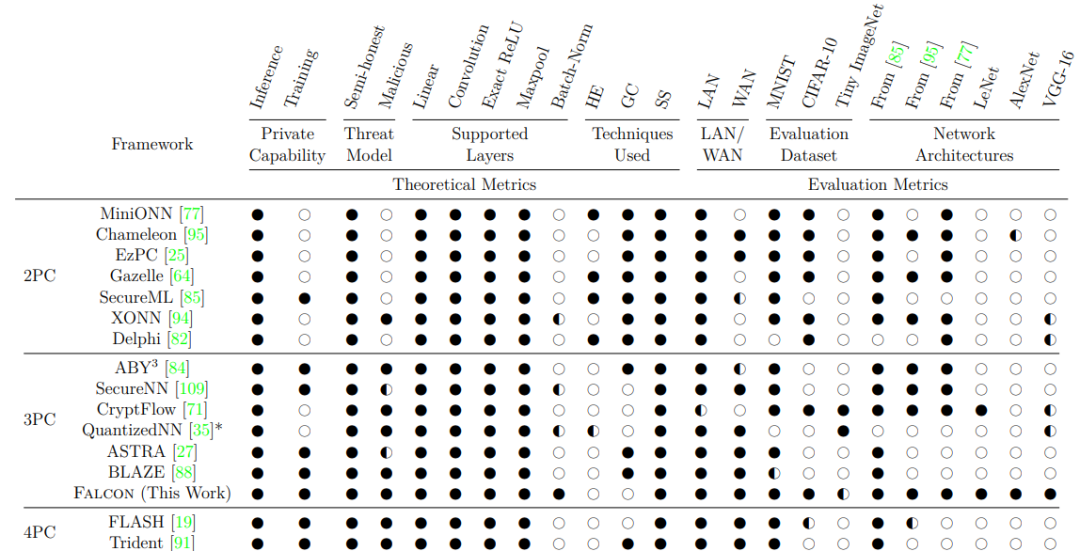
再有就是对于互联网的支持，已经成为最新趋势。 

 

 

 

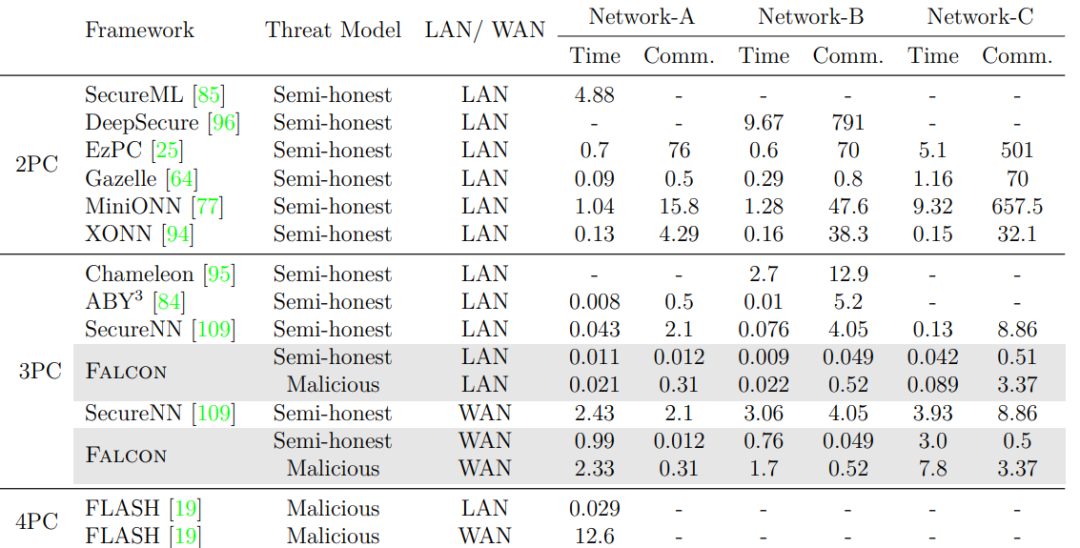
总而言之， 多方安全计算已经从早期的研究基本算术/逻辑运算，进入了按平台原子操作能力（矩阵乘法，比较），按实际需求（3方， 互联网）的方向进行研发。 背后是同态加密， 预处理等底层技术框架，平台框架的迭代发展。

 

 

 

总结

 

联邦学习， 多方安全计算， 一个从AI的角度引入安全， 一个是从安全的角度架上AI。 现在这两个方案越来越融合了， 例如SplitNN， SecureNN解决的问题就非常类似了。 相信不久，就不再区分底层技术了， 你从下图也能看到百度的PaddleFL， 微众的FATE， OpenMinded的PySyft其实是两者兼而有之。 

 

标签：SPDZ,MPC,同态,SS,算法,计算,mpc
From： https://www.cnblogs.com/Janly/p/18316081