Part 0:前置知识
Part 1:初识2-SAT
sat即Satisfiability(可满足性问题),2-set问题指对于一串布尔变量,其只有True和False两种取值,在满足若干个约束条件的前提下,对变量赋值
举个栗子:
A、B、C去吃早餐
小A认为一顿好早餐应该菜品多(a) 或 味道好(b)
小B认为一顿好早餐应该菜品少(!a) 或 价格低(c)
小C认为一顿好早餐如果味道好(b) 那么 价格高(!c)
求是否存在一种早餐可以同时满足三人的需求
这种有多种限制,且限制只关于若干变量具体的取值,同时每个变量只有是或不是两种可能性,一般为2-sat问题
Part 2:向图论前进!
让我们继续这个例子:如果存在一种早餐,它可以满足三人的条件,那么其a,b,c三个变量的取值满足(a or b) and (!a or c) and (b and !c)=true
Q:那怎么求这个方程的一组可行解呢?
首先 扔掉脑子 暴力枚举,时间复杂度\(O(2^N)\) 不要求AC其实也可以
显然时间复杂度过大,考虑其他办法。回忆一下2-sat的定义,一个变量只有False和True两种取值,所以考虑对一个布尔变量建两个点(i和i+n)用于表示第i个变量取False/True的情况。现在我们就解决了变量取值的问题,
接下来就只剩刻画限制条件了
Q:那么应该怎么去描述一个限制条件呢?
想必你一定注意到了上面加粗的字体,像“或”、“如果 那么”、“只选一个”、“不选”、“必选”这类表示两个变量之间关系的词语,通常表示几种不同的限制关系。一般情况下,我们将一条有向边(u,v)表示如果选择u则必选v,那么我们可以将大部分限制关系描述为以下几种形式:
- i,j不能同时选:思考一下,这种情况等同于“选i必不选j,选j必不选i”,转化一下,即”选i必选!j,选j必选!i",所以建边(i,!j)和(j,!i)
- 如果选i那么j必须选:等同于“选i必选j,选!j必选!i”(想想为什么)直接建边(i,j)和(!j,!i)即可
- i,j至少选一个:和上面一样,转为了“不选i必选j,不选j必选i”,所以连(!i,j)和(!j,i)
- 必选i:这个有些棘手,但是可以考虑反向构造出“选!i不合理”,即“选!i必选i”,这一定是不可能的,所以必选i,即连(!i,i)
- 必不选i:和上面一样的,连(i,!i)
Q:描述了限制条件后该怎么求解呢
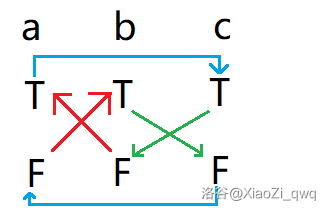
就拿举的例子来说吧,显然我们可以建出上图所示的图(T表示i点,F表示i+n点)。跑一遍tarjan后可以得到每一个点所处的连通块编号(如浅绿色的数字所示)
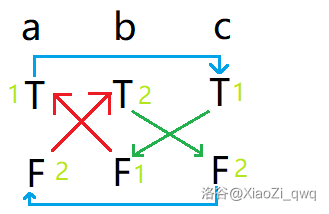
回顾我们建图和tarjan的过程,发现求SCC的过程是有先后顺序的。在一个连通块中:先找到的连通块肯定是由后找到的连通块推出来的,所以我们只需要取所处连通块编号大的点代表的值即可。
时间复杂度\(O(n+m)\)
Q:一定有解吗?如果有无解情况怎么判呢?
无解情况肯定是有的,比如“如果i必取True那么i必取False”。
显然,一个变量的如果值是唯一的,即 一个变量不能既取True又取False 。所以如果存在限制条件类似“i必取True且i必取False”,那么这种情况肯定无解。只需要在找可行解之前枚举判断即可
**Part 3:小试牛刀**
P4782 【模板】2-SAT
纯板子题,但在建图时一定要细心,实现细节见注释
#include<bits/stdc++.h>
using namespace std;
inline int read(){
register int x=0;
char c=getchar();
while(c<'0' || '9'<c) c=getchar();
while('0'<=c && c<='9') x=(x<<1)+(x<<3)+c-'0',c=getchar();
return x;
}
inline void write(int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
const int N=2001000;//由于有反点,所以需要将空间开两倍
struct Edge{ int from,to;}e[N];
int num,h[N];
void add(int f,int t){e[++num].from=h[f],e[num].to=t,h[f]=num;}
int n,m;
//tarjan部分
int dfn[N],low[N],col[N],cnt,tot;
bool instack[N];
stack<int>s;
void tarjan(int u){//只是普普通通的tarjan模板
dfn[u]=low[u]=++tot;
instack[u]=true;
s.push(u);
for(int i=h[u];i;i=e[i].from){
int v=e[i].to;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(instack[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u]){
++cnt;
while(true){
int x=s.top();s.pop();
col[x]=cnt,instack[x]=false;
if(x==u) break;
}
}
}
int main()
{
//freopen("test.in","r",stdin);
n=read(),m=read();
for(int i=1,u,v,a,b;i<=m;i++){
//u取a 或 v取b
u=read(),a=read(),v=read(),b=read();
//建图前先默念:不+n是false,+n是true
if(a==1 && b==1)
add(u,v+n),add(v,u+n);
else if(a==0 && b==1)
add(u+n,v+n),add(v,u);
else if(a==1 && b==0)
add(u,v),add(v+n,u+n);
else//if(a==0 && b==0)
add(u+n,v),add(v+n,u);
//建图小贴士:不管什么情况,一定有一条从a(或a+n)出发的边和一条从b(或b+n)出发的边
}
for(int i=1;i<=2*n;i++)//注意,这里是2*n
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++)
if(col[i]==col[i+n]){//a=!a 捏,那肯定无解捏
printf("IMPOSSIBLE");
return 0;
}
printf("POSSIBLE\n");
for(int i=1;i<=n;i++)
printf("%d ", col[i]<col[i+n]?0:1);//哪个小选哪个
return 0;
}
[P3825 [NOI2017] 游戏](https://www.luogu.com.cn/problem/P3825)
考对2-sat的深刻理解 如果直接枚举’x'的取值,会发现$O(3^d(n+m))$的时间复杂度根本过不了
回顾2-sat的过程,如果有解,那么每一个布尔变量的取值是确定的
以此作为突破口,只需要枚举x取‘a'和取’c',即可覆盖所有情况
时间复杂度\(O(2^d(n+m))\)
#include<bits/stdc++.h>
using namespace std;
inline int read(){
register int x=0;
char c=getchar();
while(c<'0' || '9'<c) c=getchar();
while('0'<=c && c<='9') x=(x<<1)+(x<<3)+c-'0',c=getchar();
return x;
}
inline void write(int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
const int N=101000;//由于有反点,所以需要将空间开两倍
struct Limit{int u,a,v,b;}lim[N];
struct Edge{ int from,to;}e[N<<1];
int num,h[N];
void add(int f,int t){e[++num].from=h[f],e[num].to=t,h[f]=num;}
int n,m,d,t[N],f[N],pos[10];//f,t数组辅助建图
//tarjan部分
int dfn[N],low[N],col[N],cnt,tot;
bool instack[N];
stack<int>st;
void tarjan(int u){//只是普普通通的tarjan模板
dfn[u]=low[u]=++tot;
instack[u]=true;
st.push(u);
for(int i=h[u];i;i=e[i].from){
int v=e[i].to;
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(instack[v])
low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u]){
++cnt;
while(true){
int x=st.top();st.pop();
col[x]=cnt,instack[x]=false;
if(x==u) break;
}
}
}
char s[N];
void init_tf(char c,int id){//预处理f,t数据
if(c=='x') pos[++pos[0]]=id;
if(c=='a') f[id]=2,t[id]=3;
if(c=='b') f[id]=1,t[id]=3;
if(c=='c') f[id]=1,t[id]=2;
}
void init(){
num=tot=cnt=0;
memset(h,0,sizeof(h));
memset(col,0,sizeof(col));
memset(low,0,sizeof(low));
memset(dfn,0,sizeof(dfn));
}
void slove(){
init();
//建图
for(int i=1,u,a,v,b;i<=m;i++){
u=lim[i].u,v=lim[i].v,a=lim[i].a,b=lim[i].b;
//建图前先默念:不+n是false,+n是true
if(u==v && a==b) continue;
if(u==v){
if(a==t[u]) add(u+n,u);
if(a==f[u]) add(u,u+n);
}
else if(a==f[u] && b==f[v])//不能同时选(f[u],t[v
add(u,v),add(v+n,u+n);
else if(a==f[u] && b==t[v])
add(u,v+n),add(v,u+n);
else if(a==t[u] && b==f[v])//t[u] t[v]
add(u+n,v),add(v+n,u);
else if(a==t[u] && b==t[v])//t[u] f[v]
add(u+n,v+n),add(v,u);
else if(b!=f[v] && b!=t[v]){
if(a==f[u]) add(u,u+n);
if(a==t[u]) add(u+n,u);
}
}
for(int i=1;i<=2*n;i++)
if(!dfn[i])
tarjan(i);
for(int i=1;i<=n;i++)
if(col[i]==col[i+n])
return;
for(int i=1;i<=n;i++)
putchar(col[i]<col[i+n]?(char)(f[i]+'A'-1):(char)(t[i]+'A'-1));
exit(0);
}
int main()
{
//freopen("test.in","r",stdin);
n=read(),d=read();
scanf("%s",s+1);
for(int i=1;i<=n;i++)
init_tf(s[i],i);
m=read();
for(int i=1;i<=m;i++)//存储限制,每一次匹配建一次图
lim[i].u=read(),lim[i].a=getchar()-'A'+1,lim[i].v=read(),lim[i].b=getchar()-'A'+1;
for(int i=0;i<(1<<d);i++){//二进制枚举
for(int j=0;j<d;j++)//如果第i位为1则认为x取'c',否则认为x取'a'
if(i&(1<<j))
init_tf('c',pos[j+1]);
else
init_tf('a',pos[j+1]);
slove();
}
printf("-1");
return 0;
}