词语表示
一种典型方法是符号表示法,\(w_1w_2\cdots w_m\)等等,等价的表示方法是one-hot表示法,此时有多少个词向量就有多少维,且没有办法表示词之间的相似性,基于连续语义空间的词语表示,向量维数和词的数量无关,是低维稠密的连续实数空间
神经网络语言模型
词向量:将每个词映射到实数向量空间中的点,设词表规模\(V\),词向量维度\(D\),look-up table是一个\(D\times V\)的矩阵,记为\(L\),里面的每一列代表一个词,该矩阵右乘一个\(V \times 1\)的ont-hot向量取出特定的词对应的词向量,\(L\)的学习:通常先随机初始化,然后通过目标函数优化词的向量表达
前馈神经网络
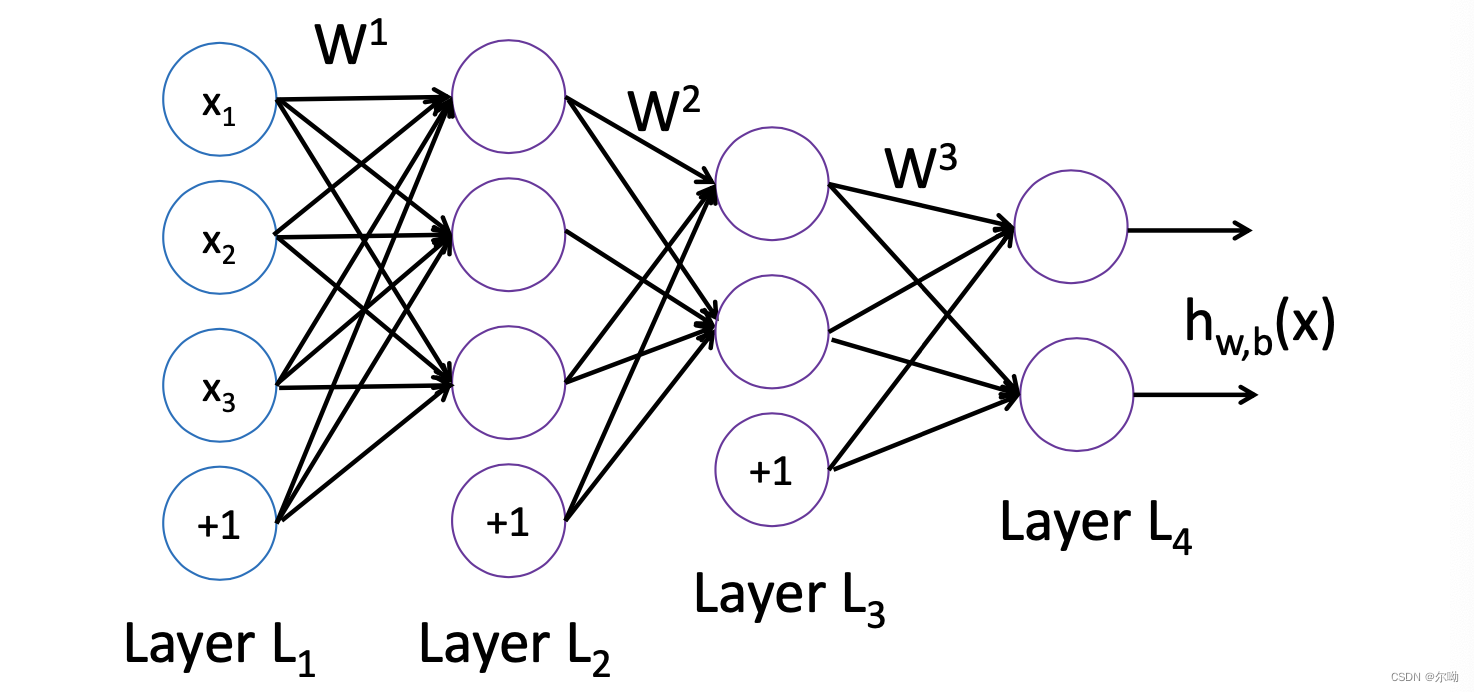
参数\(W,b\)通过反向传播算法学习,首先:
之后定义损失函数:
\[J(W,b;x,y) = \frac12||h_{W,b}(x) - y||^2 \]训练的样本为\(\{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots,(x^{(m)},y^{(m)})\}\),损失函数:
\[J(W,b) = [\frac1m\sum_{k = 1}^mJ(W,b;x^{(k)},y^{(k)}))] + \frac\lambda 2\sum_{l = 1}^{n_l - 1}\sum_{j = 1}^{s_l}\sum_{i = 1}^{s_{l + 1}}\left({W_{ij}^{(l)}}^2\right) \]参数的学习中,首先forward计算每一层每个神经元的输出,之后计算输出层也就是最后一层的输出,之后反向计算每个神经元的梯度,最后计算权重和偏差的梯度,这样既可以完成参数的学习
前馈神经网络的语言模型总结如下:
以求\(p(this|the,few,supporters,of)\)的概率为例
- 输入\(the\ few\ supporters\ of\)
- 根据look-up table得到一个由每个词的列向量concatenate得到的的矩阵,\(L:D \times V,T_w:V \times 4\),也就是得到一个\(D \times 4\)的矩阵,这个矩阵作为神经网络的输入
- 经过一个全连接层和一个Tanh激活层
- 再经过一个全连接层,输出变为\(1 \times V\)
- 经过softmax层得到输出的概率
前馈神经网络语言模型存在的问题:仅对小窗口的历史信息建模,例如n-gram仅考虑前n-1个词的历史信息
循环神经网络语言模型
例如Bush held a talk with Salon这句话,在\(t_1\)时刻,输入是Bush对应的词向量\(w_1 = [0.2,0.2]^T\)和\(h_0 = [0,0]^T\),输出的\(h_1 = U\cdot w_1 + W\cdot h_0\),这个\(h_1\)和第二个词held对应的词向量\(w_2\)作为下一时刻\(t_2\)的输入,其中\(U,W\)是共享的参数,尺寸为\(D \times D\),过程总结如下
- 输入:\(t-1\)时刻历史\(h_{t - 1}\)与\(t\)时刻输入词语的词向量\(w_t\)
- 输出:\(t\)时刻历史\(h_t\)与\(t + 1\)时刻词语的词向量\(y_t\)的概率,\(y_t\)由\(h_t\)得来,\(y_t:V\times 1\)尺寸
循环神经网络存在的问题是梯度消失和爆炸问题,参数\(W\)经过多次传递后,易发生梯度消失和爆炸,可以通过有选择的保留和遗忘,通过某种策略有选择的保留或遗忘\(t\)时刻的信息来解决LSTM
自注意机制语言模型
\[Attention(Q,K,V) = softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)V \]神经网络语言模型相关开源工具
- NNlm, 前馈神经网络语言模型(feed-forward n-gram neural language model), http://nlg.isi.edu/software/nplm/
- RNNlm, 循环神经网络语言模型(recurrent neural language model), http://rnnlm.org/;
- LSTMlm, LSTM语言模型(recurrent neural language model with LSTM unit), https://www-i6.informatik.rwth-aachen.de/web/Software/rwthlm.php
- 自我注意机制语言模型GPT(Language Model with Generative Pre-training), https://github.com/openai/gpt-2
- LSTM反向传播算法,http://arunmallya.github.io/writeups/nn/lstm/index.html#/
- Google Word2Vec, http://code.google.com/p/word2vec/