这东西对初中生挺友好的。
前置知识
-
复数
形如 \(a+bi(a,b\in \mathbb{R})\) 的数叫复数,其中 \(i^2=-1\)。
复数乘法:\((a+bi)(c+di)=ac-bd+(ad+bc)i\)。乘法分配律即可。 -
复平面
以 \(a\) 为 \(x\) 轴,\(b\) 为 \(y\)轴所组成的平面叫复平面。每个复数都对应复平面上一点。 -
单位根
以原点为圆心,\(1\) 为半径所形成的圆叫单位圆。以 \((1,0)\) 为起点,用 \(n\) 个点圆上的点将单位圆分成 \(n\) 等分。容易发现,这 \(n\) 个点正好是 \(w^n=1\) 的 \(n\) 个解。
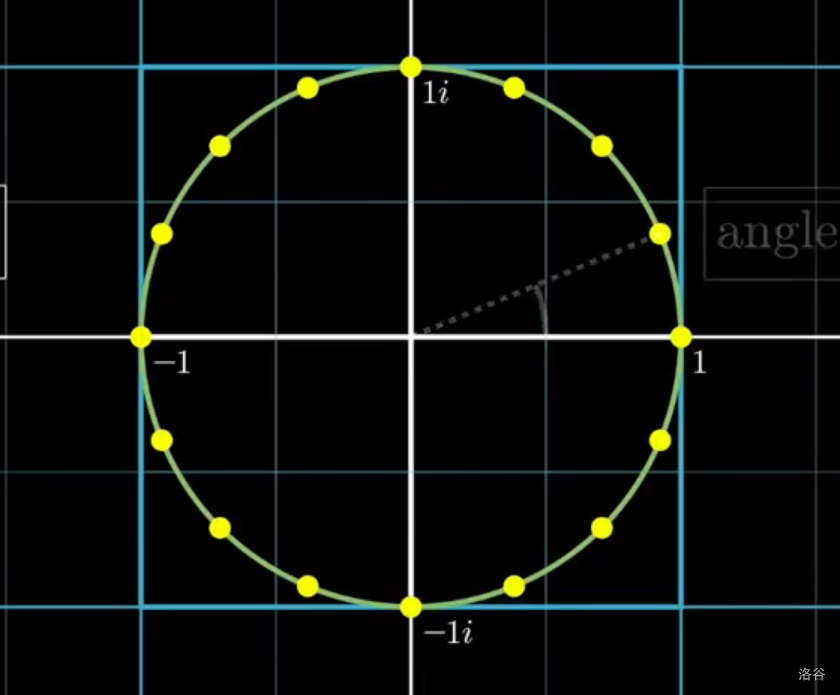
如图为一个单位圆和一些单位根。
按角度大小记这 \(n\) 个点为 \(w_n^0,w_n^1\dots w_n^{n-1}\),当 \(n\) 为 \(2\) 的次幂时,有如下性质:
- \(w_n^k=-w_n^{k+\frac{n}{2}}\),也就是说他们两两互为相反数。
- \(w_n^k=w_n^{n+k}\),说明单位根有周期性。
- 当 \(n\) 个单位根平方后,他们依然是两两互为相反数。
这些性质决定了我们为什么选它来求值。
FFT
其实就是将两个多项式转化成点值表示相乘在转回来的过程。
设 \(F(x)=\sum\limits_{i=0}^m a_ix^i\),\(m\)是两个多项式相乘后的次数。默认 \(n\) 为最小的大于 \(m\) 的 \(2\) 的次幂(方便计算)。将 \(F\) 按次数奇偶分成两个函数。
\[f_0(x^2)=\sum\limits_{i=0}^{n/2-1}a_{2i}x^{i} \]\[f_1(x^2)=\sum\limits_{i=0}^{n/2-1}a_{2i+1}x^{i} \]则
\[F(x)=f_0(x^2)+xf_1(x^2) \]显然 \(f_0,f_1\) 都是偶函数,也就是说 \(x\) 的值与 \(-x\) 是相等的。因此,我们还可以表示出
\[F(-x)=f_0(x^2)-xf_1(x^2) \]所以要取的点和多项式的次数都变为了原来的一半,可以用递归处理。但对于 \(f_0,f_1\) 而言所有的点值都是正的,不存在相反数,无法递归。所以我们尝试寻找一些更特殊的数,单位根正好满足这个性质,因为所有单位根平方后依然是两两互为相反数的。
举个例子:
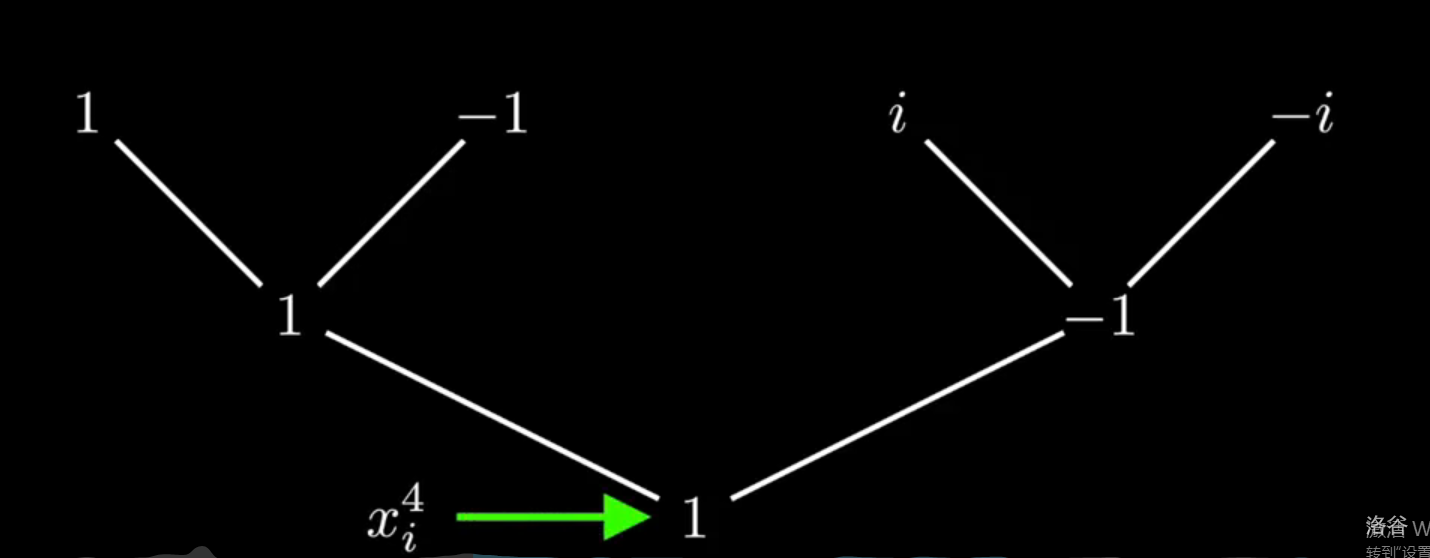
这是当 \(n=4\) 时递归的 \(x\) 值。
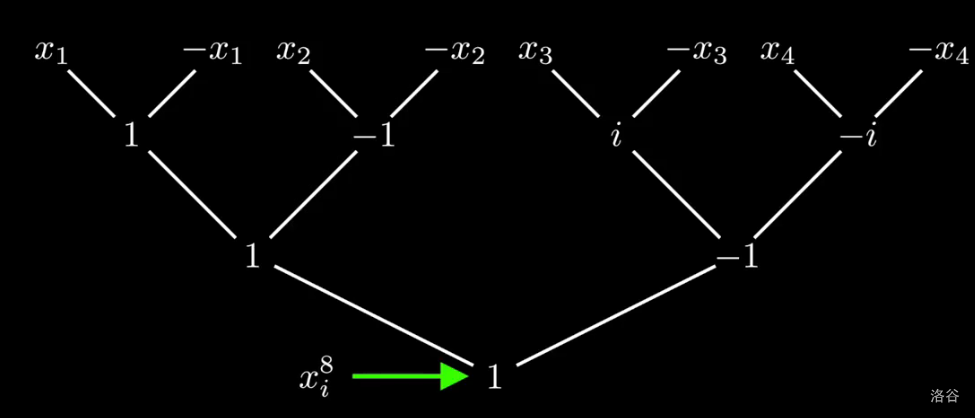
这是当 \(n=8\) 时的 \(x\) 值。
当递归到只剩一个常数项时,递归结束。
我们可以用相同的方式将另一个多项式的点值求出来。
当我们求出两个多项式点值并相乘后,如何将点值重新转化为系数呢?
我个人认为这很人类智慧。
设相乘后的多项式为 \(G(x)=\sum\limits_{i=0}^{n-1} b_ix^i\),将 \(w_n^0,w_n^{-1},\dots w_n^{1-n}\) 带入得到的多项式中进行 \(\text{FFT}\),再将所得的多项式的每一项除以 \(n\) 就是每一项对应的系数。
证明 :
设 \(c_k=\sum\limits_{i=0}^{n-1}b_i(w_n^{-k})^i\),将 \(b_i\) 用多项式表示 \(b_i=\sum\limits_{j=0}^{n-1}a_j(w_n^i)^j\),带入上式中
\[\begin{aligned} c_k&=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(w_n^i)^j)(w_n^{-k})^i\\ &=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1} a_j(w_n^i)^j(w_n^{-k})^i\\ &=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}a_j(w_n^{j-k})^i\\ &=\sum\limits_{j=0}^{n-1}a_j\sum\limits_{i=0}^{n-1}(w_n^{j-k})^i \end{aligned} \]当 \(j=k\) 时, \(c_k=na_j\)。
当 \(j \ne k\) 时
所以,\(c_k=na_j\)。\(\frac{c_k}{n}\) 就是我们要求的系数。
至此,\(\text{FFT}\) 的所有流程都已完成。
代码(递归)
bool _Start;
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define Tp template<typename T>
#define Ts template<typename T,typename... _T>
Tp il void read(T& x) {
x=0;bool f=0;char c=getchar();
for(;!isdigit(c);c=getchar()) f|=c=='-';
for(;isdigit(c);c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(f?-x:x);
}Ts il void read(T& x,_T&... y) {read(x),read(y...);}
using comp=complex<double>;
const double pi=acos(-1);
const int N=1<<21;
int n,m;
comp A[N],B[N];
void FFT(comp F[],int n,int tp) {
if(n==1) return ;
comp F0[(n>>1)+5],F1[(n>>1)+5];
for(int i=0;i<n;i+=2)
F0[i>>1]=F[i],F1[i>>1]=F[i+1];
FFT(F0,n>>1,tp),FFT(F1,n>>1,tp);
comp wn=exp(comp(0,2*pi*tp/n)),w=1;
for(int i=0;i<(n>>1);i++,w*=wn) {
F[i]=F0[i]+w*F1[i];
F[i+(n>>1)]=F0[i]-w*F1[i];
}
}
void mul(comp f[],comp g[]) {
int lim=1;
while(lim<=n+m) lim<<=1;
FFT(f,lim,1),FFT(g,lim,1);
for(int i=0;i<lim;i++) f[i]*=g[i];
FFT(f,lim,-1);
for(int i=0;i<lim;i++) f[i]/=lim;
}
bool _End;
int main() {
fprintf(stderr,"Memory: %.4lf Mib\n",abs(&_End-&_Start)/1048576.0);
read(n,m);
for(int i=0,x;i<=n;i++) read(x),A[i]=x;
for(int i=0,x;i<=m;i++) read(x),B[i]=x;
mul(A,B);
for(int i=0;i<=n+m;i++) printf("%d ",(int)(A[i].real()+0.5));
return 0;
}
优化
balabalabala.
标签:F1,limits,多项式,sum,FFT,单位根 From: https://www.cnblogs.com/kbzcz/p/18077264/FFT