记号
求和的符号有两种形式
第一种是确定界限的形式,也叫封闭形式,例如:\(\sum\limits_{k=1}^n a_k\)
第二种叫做一般形式,就是把一个或者多个条件写在 \(\sum\) 符号的下面,例如刚刚的例子可以写成 \(\sum\limits_{1\le k \le n} a_k\)
和式和递归式的转化
和式和递归式之间可以相互转化,
和式转化成递归式
\(S_n=\sum a_n\) 可以转化为 \(S_n=S_{n-1}+a_n,S_1=a_1\),后面这一项就是一个递归式子
例如:我们这里有一个递归式
\[\begin{align*} R_0=\alpha\\ R_n=R_{n-1}+\beta+\gamma n, n>0 \end{align*} \]这个可以写成通解的形式:\(R_n=A(n)\alpha+B(n)\beta+C(n)\gamma\)
由成套方法得出 \(A(n)=1,B(n)=n,C(n)=(n^2+n)/2\)
我们需要计算 \(\sum\limits_{k=0}^n(a+bk)\),只需要把 \(a=\alpha, a=\beta, b=\gamma\) 代入即可
递归式转化成和式
\[\begin{align*} T_0&=0\\ T_n&=2T_{n-1}+1, n>0 \end{align*} \]两边除以 \(2^n\) 得到
\[\begin{align*} T_0/2^0&=0\\ T_n/2^n&=T_{n-1}/2^{n-1}+1/2^n, n>0 \end{align*} \]设 \(S_n=T_n/2^n\)
\[\begin{align*} S_0&=0\\ S_n&=S_{n-1}+1/2^n, n>0 \end{align*} \]由此得到 \(S_n=\sum\limits_{k=1}^n \frac{1}{2}^k = 1-(\frac{1}{2})^n\),所以 \(T_n=2^n-1\)
和式的变换法则
经典的三条性质,注意这里的 \(K\) 是一个集合
\[\sum_{k \in K} c a_k = c \sum_{k \in K} a_k \quad \text{(分配律)} \]\[\sum_{k \in K} (a_k + b_k) = \sum_{k \in K} a_k + \sum_{k \in K} b_k \quad \text{(结合律)} \]\[\sum_{k \in K} a_k = \sum_{p(k) \in K} a_{p(k)} \quad \text{(交换律)} \]注意 \(p(k)\) 是一个双射函数,也可以理解为一个排列
例如:\(K=\{1,2,3,4\}\) 那么,\(p(k)=\{4,2,3,1\}\) 就是一个排列
当然 \(p(k)\) 可以多出几个元素例如上面那个例子 \(p(k)=\{4,2,3,1,5,6\}\) 也是可以的,\(5,6\) 不在 \(K\) 中
接下来看一个例子:\(S=\sum\limits_{0\le k \le n}(a+bk)\)
利用交换率,用 \(n-k\) 代替 \(k\),得到
\[S=\sum\limits_{0\le n-k\le n}(a+b(n-k))=\sum\limits_{0\le k \le n}(a+bn-bk) \]利用结合律,把这两个方程相加,得到
\[2S=\sum\limits_{0\le k \le n}(a+bk+a+bn-bk)=\sum\limits_{0\le k \le n}(2a+bn)=(n+1)(2a+bn) \]所以 \(S=\frac{(n+1)(2a+bn)}{2}\)
扰动法
和式中有一种非常厉害的方法叫扰动法,就是把一项从和式中去除出去,然后尝试把剩下的项变成 \(S_n\) 的形式,从而解出 \(S_n\)
例如:\(S_n=\sum\limits_{0\le k \le n}ax^k\),使用扰动法的基本套路
\[S_n+ax^{n+1}=ax^0+\sum\limits_{1\le k\le n+1} ax^{k}=ax^0+\sum\limits_{0\le k\le n}ax^{k+1}=ax^0+xS_n \]等式两边同时出现了 \(S_n\),解出 \(S_n=\frac{a-ax^{n+1}}{1-x}\)
考虑另外一个例子:\(S_n=\sum\limits_{0\le k \le n}k2^k\),考虑扰动法
\[\begin{align*} S_n+(n+1)2^{n+1}&=\sum\limits_{0\le k \le n}(k+1)2^{k+1}\\ &=2\sum\limits_{0\le k\le n}k2^k+\sum\limits_{0\le k\le n}2^{k+1}\\ &=2S_n+2^{n+2}-2 \end{align*} \]解出 \(S_n=2^{n+1}(n-1)+2\)
设未知数 \(x\),能求出 \(S_n=\sum\limits_{0\le k \le n} kx^{k}\) 的通解:
\[S_n=\frac{x-x^{n+1}(n+1)+nx^{n+2}}{(x-1)^2},x\ne 1 \]我们也可以利用求导的方法,求出 \(S_n=\sum\limits_{0\le k \le n} kx^{k}\) 的通解:
已知:\(\sum\limits_{k=0}^n x^k=\frac{1-x^{n+1}}{1-x}\),两边同时求导
\[\sum\limits_{k=0}^n kx^{k-1}=\frac{(1-x)(-(n+1)x^n)+1-x^{n+1}}{(1-x)^2}=\frac{1-(n+1)x^n+nx^{n+1}}{(1-x)^2} \]两边同时乘以 \(x\),得到
\[\sum\limits_{k=0}^n kx^k=\frac{x-x^{n+1}(n+1)+nx^{n+2}}{(x-1)^2} \]就能得到和上面扰动法一样的结果了
多重和式
多重和式对应于连续函数的积分,可以利用积分的一些思维来思考多重和式
对于自变量相互无关的情况很好理解
\[\begin{align*} \sum\limits_{1\le j,k\le 3}a_jb_k&=a_1b_1+a_1b_2+a_1b_3+a_2b_1+a_2b_2+a_2b_3+a_3b_1+a_3b_2+a_3b_3\\ &=a_1(b_1+b_2+b_3)+a_2(b_1+b_2+b_3)+a_3(b_1+b_2+b_3)\\ &=(a_1+a_2+a_3)(b_1+b_2+b_3)\\ &=\left(\sum\limits_{1\le j\le 3}a_j\right)\left(\sum\limits_{1\le k\le 3}b_k\right) \end{align*} \]一个多重和式可以转化成两个和式相乘的形式,前提是 \(J=K\),其中 \(j\in J,k\in K\),这一点在级数相乘的时候极为有效
在具体求多重和式的时候,往往是一层一层往外求,理论上来说,先固定住哪个自变量都是无所谓的,所以我们可以交换求和符号的位置
设 \(P(j,k)\) 返回的是 \(j,k\) 是否满足某种性质,那么有:
\[\sum\limits_{j\in J}\sum\limits_{k\in K}a_{j,k}[P(j,k)]=\sum\limits_{k\in K}\sum\limits_{j\in J}a_{j,k}[P(j,k)] \]讨论自变量之间有某些限制
一种比较常见的方式:\(1\le j \le k \le n\),我们可以通过画图找出需要求和的元素
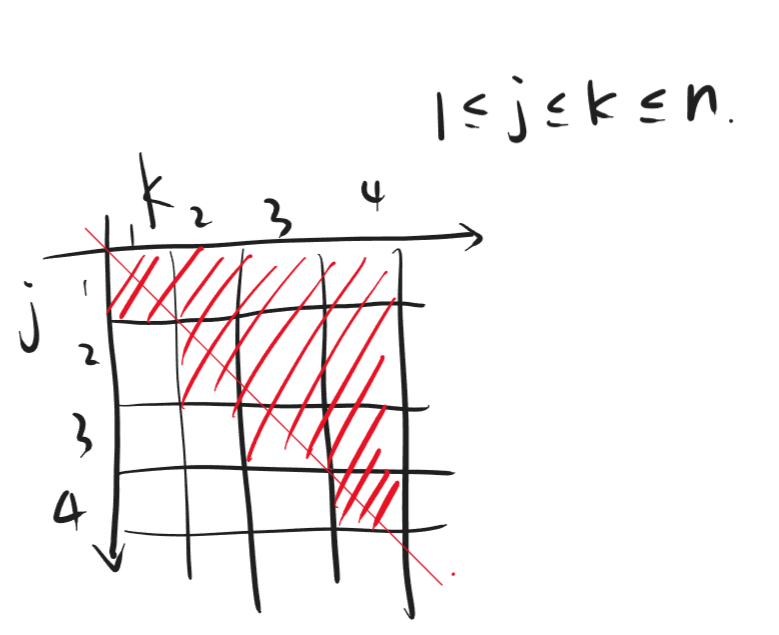
可以看到对角线以及右上角的那一块都是需要求和的
另外一种常见的方式 \(1\le j,k\le n,j+k=n\),画出图来是按对角线求和
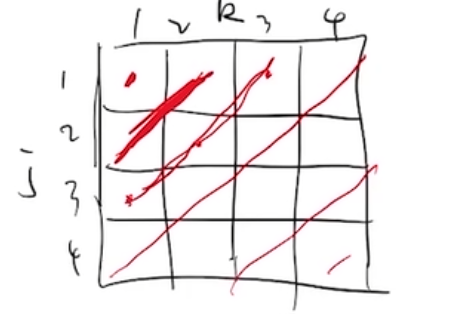
这种求和方法有一种自己的名字,叫卷积(Convolution)
例一:求 \(\sum\limits_{1\le j\le k\le n}a_ja_k\)

可以看到要求部分是右上三角形
由于图标的对称性,可以得到 \(S_{\text{左下}}=S_{\text{右上}}\)
由容斥原理:\(S_{\text{左下}}+S_{\text{右上}}=S_{\text{全部}}-S_{\text{对角线}}\)
于是就能得我们想要的答案了
\[S_{\text{右上}}=\sum\limits_{1\le j\le k\le n}a_ja_k=\frac{1}{2}\left(\left(\sum\limits_{k=1}^na_k\right)^2+\sum\limits_{k=1}^n a_k^2\right) \]例二:求 \(S=\sum\limits_{1\le j < k \le n}(a_k-a_j)(b_k-b_j)\)
交换 \(j,k\) 仍然由对称性:
\[S=\sum\limits_{1\le k< j\le n}(a_j-a_k)(b_j-b_k)=\sum\limits_{1\le k< j\le n}(a_k-a_j)(b_k-b_j) \]所以得到答案
\[2S=\sum\limits_{1\le j, k\le n}(a_j-a_k)(b_j-b_k)-\sum\limits_{1\le j=k\le n}(a_j-a_k)(b_j-b_k) \]显然,第二个和式等于 \(0\),把第一个和式展开
\[\begin{align*} 2S&=\sum\limits_{1\le j, k\le n}a_jb_j-\sum\limits_{1\le j, k\le n}a_jb_k-\sum\limits_{1\le j, k\le n}a_kb_j+\sum\limits_{1\le j, k\le n}a_kb_k\\ &=2n\sum\limits_{1\le k\le n}a_kb_k-2\left(\sum\limits_{k=1}^n a_k\right)\left(\sum\limits_{k=1}^n b_k\right) \end{align*} \]所以就得出了 \(S=n\sum\limits_{1\le k\le n}a_kb_k-\left(\sum\limits_{k=1}^n a_k\right)\left(\sum\limits_{k=1}^n b_k\right)\)
-
若 \(\{a\},\{b\}\) 都是升序的,那么显然 \(S\ge 0\),所以 \(n\sum\limits_{1\le k\le n}a_kb_k-\left(\sum\limits_{k=1}^n a_k\right)\left(\sum\limits_{k=1}^n b_k\right) \ge n\)
,可以推出不等式:\(n\sum\limits_{1\le k\le n}a_kb_k\ge \left(\sum\limits_{k=1}^n a_k\right)\left(\sum\limits_{k=1}^n b_k\right)\) -
若 \(\{a\}\) 是升序的,\(\{b\}\) 是降序的,那么显然 \(S\le 0\),所以 \(n\sum\limits_{1\le k\le n}a_kb_k-\left(\sum\limits_{k=1}^n a_k\right)\left(\sum\limits_{k=1}^n b_k\right) \le n\)
,可以推出不等式:\(n\sum\limits_{1\le k\le n}a_kb_k\le \left(\sum\limits_{k=1}^n a_k\right)\left(\sum\limits_{k=1}^n b_k\right)\)
这两个不等式叫做 切比雪夫单调不等式
例三
\[S_n=\sum\limits_{1\le j<k\le n}\frac{1}{k-j} \]我们可以用 \(k-j\) 替换 \(j\),然后固定 \(k\)
\[\begin{align*} S_n&=\sum\limits_{1\le k \le n}\sum\limits_{1\le j\le k}\frac{1}{k-j}\\ &=\sum\limits_{1\le k \le n}\sum\limits_{0\le j\le k-1}\frac{1}{j}\\ &=\sum\limits_{1\le k \le n}H_{k-1}\\ &=\sum\limits_{0\le k \le n-1}H_{k}\\ \end{align*} \]其中 \(H_k\) 是调和级数,我们对调和级数有公式,但是对于调和级数求和没有公式,说明固定 \(k\) 走不通考虑固定 \(j\)
\[\begin{align*} S_n&=\sum\limits_{1\le j < n}\ \sum\limits_{j < k\le n}\frac{1}{k-j}\\ &=\sum\limits_{1\le j \le n}\ \sum\limits_{j<k+j\le n}\frac{1}{k+j-j}\\ &=\sum\limits_{1\le j \le n}\ \sum\limits_{0<k\le n-j}\frac{1}{k}\\ &=\sum\limits_{1\le j \le n}H_{n-j}\\ &=\sum\limits_{0\le j \le n-1}H_{j}\\ \end{align*} \]还是回到了调和级数求和的问题,考虑按对角线求和
\[\begin{align*} S_n&=\sum\limits_{1\le j < n}\ \sum\limits_{j < k\le n}\frac{1}{k-j}\\ &=\sum\limits_{1\le j \le n}\ \sum\limits_{j<k+j\le n}\frac{1}{k+j-j}\\ &=\sum\limits_{1\le j \le n}\ \sum\limits_{0<k\le n-j}\frac{1}{k}\\ &=\sum\limits_{0<k<n}\ \sum\limits_{1\le j\le n-k}\frac{1}{k}\\ &=\sum\limits_{0<k<n}\frac{n-k}{k}=\sum\limits_{0<k<n}(\frac{n}{k}-1)\\ &=n\sum\limits_{1\le k\le n}\frac{1}{k}-\frac{n}{n}-(n-1)\\ &=nH_n-n \end{align*} \]我们还可以从几何的层面来理解这个式子:
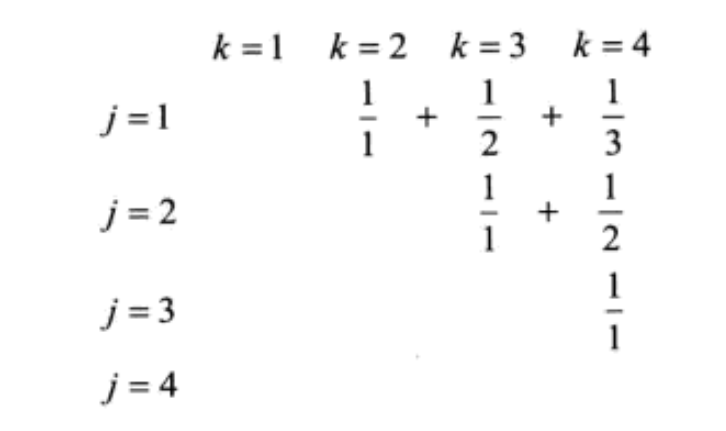
刚开始的几次我们按照行和列求和,都会得到一个调和级数求和的式子,最后一种方式是按照对角线,这里得到 \(\frac{3}{1}+\frac{2}{2}+\frac{1}{3}\)
一般性方法
这一节基本上就是总结性质的,把前面介绍的方法综合运用一下
要求一个立方和 \(S_n=\sum\limits_{k=0}^n k^2, \ n \ge 0\)
方法0:查找公式
OEIS 能帮我们很好的查找公式
得到的答案是 \(S_n=\frac{n(n+1)(2n+1)}{6}\)
方法1:数学归纳法
已知:\(S_n=\frac{n(n+\frac{1}{2})(n+1)}{3}\)
显然 \(S_0=0\) 成立,假设 \(n>0\) 时,\(S_{n-1}=\frac{(n-1)(n-\frac{1}{2})n}{3}\) 成立,有:\(S_n=S_{n-1}+S\)
\[\begin{align*} 3S_n&=(n-1)(n-\frac{1}{2})(n)+3n^2 \\ &=n^3+\frac{3}{2}n^2+\frac{1}{2}n \\ &=n(n+1)(n+\frac{1}{2}) \end{align*} \]所以 \(S_n=\frac{n(n+\frac{1}{2})(n+1)}{3}\) 对所有 \(n\ge 0\) 都成立
方法2:扰动法
\[\begin{align*} S_n+(n+1)^2&=\sum\limits_{k=0}^{n}(k+1)^2=\sum\limits_{k=0}^n(k^2+2k+1)\\ &=\sum\limits_{k=0}^{n}k^2+2\sum\limits_{k=0}^nk+\sum\limits_{k=0}^n1\\ &=S_n+2\sum\limits_{k=0}^nk+n+1 \end{align*} \]惊人的发现,我们需要求的 \(S_n\) 被消掉了,留下一个 \(\sum\limits_{k=0}^nk=\frac{(n+1)^2-(n+1)}{2}=\frac{n(n+1)}{2}\)
我们猜想能不能用立方和来把平方和求出来,设 \(T_n=\sum\limits_{k=0}^n k^3\)
\[\begin{align*} T_n+(n+1)^3&=\sum\limits_{k=0}^n(k+1)^3=\sum\limits_{k=0}^n(k^3+3k^2+3k+1)\\ &=\sum\limits_{k=0}^n k^3+3\sum\limits_{k=0}^n k^2+3\sum\limits_{k=0}^n k+\sum\limits_{k=0}^n 1\\ &=T_n+3S_n+3\frac{n(n+1)}{2}+n+1 \end{align*} \]\(T_n\) 被消掉了,留下我们需要求的 \(S_n\),这样 \(3S_n=(n+1)^3-3\frac{n(n+1)}{2}-(n+1)\)
所以 \(S_n=\frac{n(n+1)(n+\frac{1}{2})}{3}\)
方法3:建立成套方法
还是老规矩,建立成套方法,设:
\[\begin{align*} R_0&=\alpha, n=0\\ R_n&=R_{n-1}+\beta+\gamma n+\delta n^2, n>0 \end{align*} \]解的一般形式就是:\(R_n=A(n)\alpha+B(n)\beta+C(n)\gamma+D(n)\delta\)
我们已知,\(\delta=0\) 时,\(A(n)=1,B(n)=n,C(n)=(n^2+n)/2\)
现在要求 \(D(n)\) 和他们的关系,设 \(R_n=n^3\),有 \(n^3=(n-1)^3+\beta+\gamma n+\delta n^2\)
可得:\(\alpha=0\),\(\beta=1\),\(\gamma=-3\),\(\delta=3\),代入:\(3D(n)-3C(n)+B(n)=n^3\)
就把 \(D(n)\) 接出来了,\(D(n)=n^3-3\frac{n(n+1)}{2}+n=\frac{n(n+\frac{1}{2})(n+1)}{3}\)
我们需要求的和式 \(S_n\) 转化成递归式子,只需要令 \(\alpha=\beta=\gamma=0\) 以及 \(\delta=1\)
则 \(S_n=D(n)\)
方法4:用积分替换和式
我们已知 \(\int_{0}^{n}x^2dx=\frac{n^3}{3}\),显然,和式和积分之间的差距并不差,只是差一个误差
我们设这个误差为 \(E_n=S_n-\frac{n^3}{3}\),通过 \(S_n\) 的递归式,我们能得出 \(S_n=S_{n-1}+n^2\)
\[\begin{align*} E_n&=S_n-\frac{n^3}{3}=S_{n-1}+n^2-\frac{n^3}{3}\\ &=E_{n-1}+\frac{(n-1)^3}{3}+n^2-\frac{n^3}{3}\\ &=E_{n-1}+n-\frac{1}{3} \end{align*} \]于是,我们就得到了 \(E_n\) 的递推式,\(E_n=E_{n-1}+n-\frac{1}{3}\),\(E_0=0\)
很容易算出 \(E_n\) 的通项公式为 \(E_n=\frac{n(n+1)}{2}-\frac{n}{3}\),所以 \(S_n=E_n+\frac{n^3}{3}=\frac{n(n+1)(n+\frac{1}{2})}{3}\)
方法5:展开和放缩
这种方法极具技巧性,把一个一重和式转化成二重和式
\[\begin{align*} S_n&=\sum\limits_{k=0}^n k^2=\sum\limits_{1\le j \le k \le n} k \\ &=\sum\limits_{1\le j \le n}\ \sum\limits_{j\le k\le n} k\\ &=\sum\limits_{1\le j \le n} (\frac{j+n}{2})(n-j+1)\\ &=\frac{1}{2}\sum\limits_{1\le j \le n} \left(n(n+1)+j-j^2\right)\\ &=\frac{1}{2}n^2(n+1)+\frac{1}{4}n(n+1)-\frac{1}{2} S_n\\ \end{align*} \]这样等式两边都出现了 \(S_n\),解出 \(S_n=\frac{n(n+1)(2n+1)}{6}\)
有限微积分
我们类似于积分和微分的思维,在离散域上定义有限微积分,定义差分算子 \(\Delta f(x)\) 是 \((f(x+h)-f(x))/h\) 当 \(h=1\) 时的值
还需要定义两种特殊的次幂:
- 下降阶乘幂 \(x^{\underline{m}}=x(x-1)\cdots(x-m+1),\ m \ge 0\)
- 上升阶乘幂 \(x_{\overline{m}}=x(x+1)\cdots(x+m-1),\ m \ge 0\)
我们为什么要定义这样奇特的形式呢,因为这样求差分的时候会和微分有很多共同点
\[\begin{align*} \Delta x^{\underline{m}}&=(x+1)^{\underline{m}}-x^{\underline{m}}\\ &=(x+1)x(x-1)\cdots(x-m+2)-x(x-1)(x-2)\cdots(x-m+1)\\ &=(x+1-(x-m+1))x(x-1)(x-2)\cdots(x-m+2)\\ &=mx(x-1)(x-2)\cdots(x-m+2)\\ &=m x^{\underline{m-1}} \end{align*} \]有限微积分也存在类似于微积分基本定理的东西
\[g(x)=\Delta f(x)\Longleftrightarrow \sum g(x)\delta x=f(x)+C \]这里的 \(\sum g(x)\delta x\) 是 \(g(x)\) 的不定和式,这里的 \(C\) 可以是周期为 \(1\) 的任意函数
大名鼎鼎的牛顿-莱布尼茨公式在有限微积分中也有体现 \(\sum_a^b g(x) \delta x = f(x) \bigg|_a^b = f(b) - f(a)\)
思考 \(\sum_a^b g(x) \delta x = f(x) \bigg|_a^b = f(b) - f(a)\) 当,上下限相同时:
\[\sum_a^a g(x) \delta x = f(x) \bigg|_a^a = f(a) - f(a) = 0 \]当上下限差 \(1\) 时:
\[\sum_a^{a+1} g(x) \delta x = f(x) \bigg|_a^{a+1} = f(a+1) - f(a)=\Delta f(x)=g(x) \]着预示着和传统的求和符号有点不同,可以理解为 \(\sum_{a}^b g(x)\delta x=\sum\limits_{k=a}^{b-1}g(k)=\sum\limits_{a\le k<b}g(k), b\ge a\)
也就是说,如果存在能找到一个 \(f(x)\) 使得 \(f(x+1)-f(x)=g(x)\),那么理论上来说就可以求 \(\sum g(x)\) 这类的和了
我们尝试去求类似于原函数的东西 \(f(x)\)
比如:\(g(x)=x^{\underline{m}}\),\(f(x)=\frac{x^\underline{m+1}}{m+1}\)
我们用前面的例子,求 \(\sum\limits_{0\le k < n} k^2\) 已知 \(k^2=k^\underline{2}+k^\underline{1}\),所以
\[\sum\limits_{0\le k < n} k^2=\frac{n^\underline{3}}{3}+\frac{n^\underline{2}}{2}=n(n-1)\left(n-2+\frac{3}{2}\right)=\frac{1}{3}n\left(n-\frac{1}{2}\right)(n-1) \]利用 \(n+1\) 替换 \(n\) 就可以得到 \(S_n\) 了
尝试继续推广无限微积分,考虑下降次幂为负数的情况,\(x^{\underline{m}},\ m<0\)
观察:
- \(x^{\underline{3}}=x(x-1)(x-2)\),\(x^{\underline{2}}=x(x-1)\) 两个相除得出 \(x-2\)
- \(x^{\underline{2}}=x(x-1)\),\(x^{\underline{1}}=x\) 两个相除得出 \(x-1\)
- \(x^{\underline{1}}=x\),\(x^{\underline{0}}=1\) 两个相除得出 \(x\)
于是找规律得出 \(x^{\underline{-1}}=\frac{1}{x+1},x^\underline{-2}=\frac{1}{(x+1)(x+2)}\),\(x^{-m}=\frac{1}{(x+1)(x+2)\cdots(x+m)}\)
通常的幂法则:\(x^{m+n}=x^mx^n\),推广到有限微积分就变成了 \(x^\underline{m+n}=x^\underline{m}(x-m)^\underline{n}\)
现在确认下降幂的差分性质在 \(m<0\) 是否成立也就是 \(\Delta x^\underline{m}=mx^\underline{m-1}\)
如果 \(m=-2\),有
\[\begin{align*} \Delta x^\underline{-2}&=(x+1)^\underline{-2}-x^\underline{-2}\\ &=\frac{1}{(x+2)(x+3)}-\frac{1}{(x+1)(x+2)}\\ &=\frac{(x+1)-(x+3)}{(x+1)(x+2)(x+3)}\\ &=\frac{-2}{(x+1)(x+2)(x+3)}\\ &=-2x^\underline{-3} \end{align*} \]说明求和性质对 \(m<0\) 也成立,即 \(\sum_a^b x^\underline{m}\delta x=\frac{x^\underline{m+1}}{m+1}\bigg|_a^b,\ m \ne 1\)
现在考虑 \(m=1\) 的时候,对于微积分,我们又 \(\int_a^b x^{-1}dx=\ln x\bigg|_{a}^b\)
我们需要在有限微积分中找一个类似于 \(\ln x\) 的函数 ,这个函数的差分为 \(\frac{1}{x+1}\)
很显然能得到这个函数就是 \(H_x\),于是就得到了求和的完整形式
\[\sum_{a}^{b} x^{-m} \delta x = \begin{cases} \left. \frac{x^{m+1}}{m+1} \right|_{a}^{b}, & m \neq -1, \\ \left. H_{x} \right|_{a}^{b}, & m = -1. \end{cases} \]类似的,我们需要找一个 \(e^x\) 类似物,根据定义 \(d(e^x)=e^x\),所以有 \(f(x+1)-f(x)=f(x)\Longleftrightarrow f(x+1)=2f(x)\),即 \(f(x)=2^x\)
\(c^x\) 的差分也相当简单,即对任意的 \(c\) 有
\[\Delta (c^x) = c^{x+1} - c^x = (c - 1) c^x. \]那么,\(c\ne 1\) 时,\(c^x\) 的原函数就是 \(c^x/(c-1)\)
两个相乘的函数求微分:\(d(uv)=udv+vdu\),两边同时积分得到分部积分法的公式:\(\int udv=uv-\int vdu\)
有限微积分也类似
\[\begin{aligned} \Delta \left( u(x)v(x) \right) &= u(x+1)v(x+1) - u(x)v(x) \\ &= u(x+1)v(x+1) - u(x)v(x+1) + u(x)v(x+1) - u(x)v(x) \\ &= u(x)\Delta v(x) + v(x+1)\Delta u(x). \end{aligned} \]这里的 \(v(x+1)\) 看着很烦,所以定义一个位移算子 \(\text{E} f(x)=f(x+1)\)
所以乘积差分法则可以写为:
\[\Delta(uv)=u\Delta v+\text{E}v\Delta u \]两边求和得:
\[\sum u\Delta v=uv-\sum \text{E}v\Delta u \]有限微积分和无限微积分对应着离散和连续,有很多共通点,在下列表中给出

来看几个例子:
例一:
\[\begin{align*} \sum_{k=0}^{n} k 2^k &= \sum_{0}^{n+1} x 2^x \delta x \\ &= x 2^x - 2^{x+1} \bigg|_{0}^{n+1}\\ &= \left( (n+1) 2^{n+1} - 2^{n+2} \right) - (0 \times 2^0 - 2^1)\\ &= (n-1) 2^{n+1} + 2 \end{align*} \]例二: 求 \(\sum\limits_{0\le k < n} kH_k\)
先求原函数,根据分部积分法则:
\[\begin{align*} \sum xH_x\delta x&=\frac{x^\underline{2}}{2}H_x-\sum\frac{(x+1)^\underline{2}}{x}x^\underline{-1}\delta x\\ &=\frac{x^\underline{2}}{2}H_x-\frac{1}{2}\sum x^\underline{1}\delta x\\ &=\frac{x^\underline{2}}{2}H_x-\frac{x^\underline{2}}{4}+C \end{align*} \]然后把上下限代入:
\[\sum\limits_{0\le k <n} kH_k=\sum_{0}^{n}xH_x\delta x=\frac{n^\underline{2}}{2}\left(H_n-\frac{1}{2}\right) \]无限和式
引用大乌拉的一句话:
我们对无穷的东西几乎一无所知
这一章书上举了几个具体的例子,都在表达无穷和式似乎没有我们想象的这么简单
标签:le,frac,limits,sum,underline,第二章,align From: https://www.cnblogs.com/martian148/p/18286438