思路

对于每一个 7，我们都可以抽象为这样一个图形：

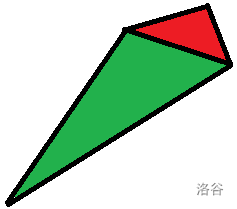
如果有两个 7，无论它是否有重合部分，红色部分是不需要判断的，只需要看绿色的部分。

因此，我们的问题就简化为了三角形，而不是四边形。

对于所有的 7，都有一个公共顶点：\((0,0)\) 点。

所以，我们可以引出一个叫斜率的概念来判断这些三角形是否有重合部分。

这里我们定义斜率为 \(y\) 坐标与 \(x\) 坐标的比值。

对于这道题，我们可以先看一下P1803 凌乱的yyy / 线段覆盖。

我们可以将这道题的三角形的斜率类比成线段，将绿色三角形的上面的那条边看做线段的左端点，下面的那条边看做线段的右端点。

然后，我们直接按照那题的贪心方法搞就行了。

我们判断两条边是否相交，我们直接判断斜率即可。

Code

#include <bits/stdc++.h>  
#define int long long  
#define re register  
  
using namespace std;  
  
const int N = 2e5 + 10;  
int n,l,ans;  
  
struct node{  
    int x;  
    int y;  
    int xx;  
    int yy;  
    bool operator <(const node &t) const{  
        return yy * t.xx < t.yy * xx;//判断斜率，原式为：yy / xx < t.yy / t.xx，这里为了避免精度问题，通过移项将除法改变为乘法   
    }  
}arr[N];  
  
inline int read(){  
    int r = 0,w = 1;  
    char c = getchar();  
    while (c < '0' || c > '9'){  
        if (c == '-') w = -1;  
        c = getchar();  
    }  
    while (c >= '0' && c <= '9'){  
        r = (r << 3) + (r << 1) + (c ^ 48);  
        c = getchar();  
    }  
    return r * w;  
}  
  
signed main(){  
    n = read();  
    for (re int i = 1;i <= n;i++){  
        int a,b;  
        a = read();  
        b = read();  
        arr[i] = {a,b - 1,a - 1,b};//存储两个点的坐标   
    }  
    sort(arr + 1,arr + 1 + n);//排序   
    for (re int i = 1;i <= n;i++){  
        if (arr[i].y * arr[l].xx >= arr[l].yy * arr[i].x){//判断两个角是否有相交   
            ans++;//更新  
            l = i;  
        }  
    }  
    printf("%lld",ans);  
    return 0;  
}