前言:之前写过两篇第七章习题解析,本篇主要是补充,将之前没有来得及写上的习题补充完整,顺便归个类。前两篇看主页吧,不指路了。
习题7.4部分
1(1).根据下列不变因子组写出有理标准型:
解:排除0次多项式,的友阵为(1),
的展开式为
,则其友阵为
可以得到有理标准型为.
2(1).求下列矩阵的有理标准型。
解:(不想写了只说思路吧,化成特征矩阵形式,然后找各阶行列式因子,然后大除以小,再写友阵)。
5.证明:n阶矩阵A的特征多项式和极小多项式相等的充分必要条件是 的行列式因子为
的行列式因子为 。
。
证明:特征多项式因子是所有不变因子的乘积
而极小多项式是最大的不变因子,
又因为
则如果两者相等,可以显而易见除了极小多项式之外的不变因子全都是1.
7.若k是满足 的最小正整数,则称A为k次幂零阵,请写出A的最后一个不变因子,并证明:所有n阶n次幂零阵彼此相似。
的最小正整数,则称A为k次幂零阵,请写出A的最后一个不变因子,并证明:所有n阶n次幂零阵彼此相似。
证明:设A的特征值是,显而易见这个
是A的极小多项式,所以A的最后一个不变因子是
,
想要证明所有n阶n次幂零阵彼此相似,假设两个n阶n次矩阵A,B。
是n阶的n次幂零阵,所以
,所以由第五题结论可以知道,他们特征矩阵的行列式因子一样,都为
,所以两个矩阵相似。
8.若n阶矩阵A有n个不同的特征值,求证:A的特征多项式等于极小多项式。
证明:n阶矩阵有n个不同的特征值,所以,
的因式全都是一次不可约因式,而极小多项式和特征多项式有相同的根,他们就会有相同的一次不可约因式,所以
.
9.设数域 上的n阶矩阵A的特征多项式
上的n阶矩阵A的特征多项式 其中
其中 是
是 上互异的首一不可约多项式,求证:A的有理标准型只有一个Frobenius块,并且A在复数域上可对角化。
上互异的首一不可约多项式,求证:A的有理标准型只有一个Frobenius块,并且A在复数域上可对角化。
证明:都是互异的首一不可约多项式,则极小多项式和特征多项式相等(这句话我已经说倦了)
A的不变因子是,所以A的有理标准型只有一个有理块(Frobenius块)。
一个多项式在复数域上一定能分解成n个一次因式的乘积。
,
又互异且首一不可约。
所以一定会有n个不同的特征值。
A在复数域上可对角化。
10.设数域 上的n阶矩阵A的不变因子是
上的n阶矩阵A的不变因子是 ,其中
,其中 是非常数的首一多项式
是非常数的首一多项式 ,求证:对A的任一特征值
,求证:对A的任一特征值 ,
, 其中记号
其中记号 表示:若a=b,取值为1;若
表示:若a=b,取值为1;若 ,取值为0。
,取值为0。
证明:易知,设A对应的某个约当块为
,
,
易知,所以
,
又,
,
又,
。
12.设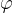 是数域
是数域 上n维线性空间V上的线性变换,其极小多项式的次数等于n,又
上n维线性空间V上的线性变换,其极小多项式的次数等于n,又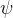 是V上的另一个线性变换,满足
是V上的另一个线性变换,满足 ,求证:
,求证: ,其中
,其中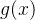 是一个
是一个 上次数不超过n-1的多项式。
上次数不超过n-1的多项式。
证明:极小多项式的次数和特征多项式的次数相等。
V恰好是由某个向量
生成的
循环空间*(说明在题末)
则存在一组基:,
则存在
*设,
则的友阵为
,
则存在一组基:,
使得
在此基下的矩阵为
的友阵。
习题7.6部分
1(2).已知矩阵的下列初等因子组: ,写出Jordan标准型。
,写出Jordan标准型。
的对应若当块为
的对应若当块为
,
的对应若当块为
,
然后写成准对角阵的形式即可。
2(1).求非异阵P,使得 为Jordan标准型。
为Jordan标准型。
思路:
先求出特征值。
判断矩阵的秩,然后判断若当块的个数。
写出若当标准型。
用,
,得到P
4.设n阶矩阵A适合 且A的秩为r,试求A的Jordan标准型。
且A的秩为r,试求A的Jordan标准型。
解:易知,是一个零化多项式,A的极小多项式要么是
要么是
,但是矩阵的特征值一定是0,再由某个特征值的约当块个数公式:
得到N=n-r
当A的极小多项式是时,A=0,约当标准型为零矩阵。
当A的极小多项式时时,易知剩下的初等因子都是
或者
。
接下来,假设有a个,b个
。
容易知道a+2b=n
a+b=n-r
解得a=n-2r,b=r.
A的Jordan标准型为.
5.设n阶矩阵A适合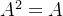 且A的秩为r,试求A的Jordan标准型。
且A的秩为r,试求A的Jordan标准型。
解:f(λ) =
− λ = λ(λ − 1) 是 A 的零化多项式,所以极小多项式 m(λ) 无重根,且 A 的特征值只能是 0 或 1。
A 可以对角化. 再根据 r(A) = r 可知 A 的 Jordan 标准型为 diag{1, . . . , 1, 0, . . . , 0},其中有 r 个 1。
6.设n(n>1)阶矩阵A的秩为1,试求A的Jordan标准型。
解:(秩为1可以写成两个n维列向量的乘积)
设,而
,
则,是A的零化多项式,由5可知,A可以对角化,A的特征值为0或
又 r(A) =1得到,A 的 Jordan 标准型为 diag{tr(A),0, . . . , 0}.
出现了一个很重要的结论:当一个矩阵可以对角化的时候,非零特征值的个数就是矩阵的秩,当一个矩阵不能够对角化的时候,上述不成立,但是非零特征值的个数小于矩阵的秩。
8.设n阶矩阵A的极小多项式的次数等于n,求证:A的Jordan标准型中各个Jordan块的主对角线元素彼此不同。
解:由题知:极小多项式的一次多项式两两互素,则一次多项式没有相同的根,A有n个不同的特征值,则各个Jordan块的主对角线元素彼此不同。
9.设A是n阶复矩阵且存在整整数K,使得 ,求证:A相似于对角阵。
,求证:A相似于对角阵。
证明:(首先一眼就能看出A是一个幂幺矩阵,一定能对角化。)
当k=1时,A是单位阵,显然能够对角化。
当k>1时,A的零化多项式为,
又A是n阶复矩阵,所以有n个n次单位根。所以A有n个不同的特征值。则A可以对角化,所以A相似于对角阵。
10.设有理数域上n阶矩阵A的特征多项式的所有不可约因式是 ,又A的极小多项式是四次多项式,求证:A在复数域上必相似于对角阵。
,又A的极小多项式是四次多项式,求证:A在复数域上必相似于对角阵。
证明:因为A的极小多项式和特征多项式有相同的不可约因式,所以A的极小多项式为
因为一个多项式在复数域上必有根,
,
而且互不相等。
所以A的极小多项式没有重根,也就意味着,A在复数域上一定相似于对角阵。
11.设n阶矩阵A的全体不同特征值为 ,令
,令 ,求证:A可对角化的充分必要条件是
,求证:A可对角化的充分必要条件是 。
。
证明:
充分性:
如果,而且
的根为A的全体特征值,A的极小多项式
的根也是A的全体特征值,所以
,
又为不同的一次因式的乘积,
则,又
是首一的,所以
,而
没有重根,所以A可对角化。
必要性:
若A可以对角化,所以A的极小多项式没有重根,易知,所以
。
12.设A是n阶复矩阵,求证:A相似于分块对角阵diag{B,C},其中B是幂零矩阵,C是非异阵。
证明:当A是可逆的时候,A没有为0的特征值,自然不会有主对角元为0的若当块。A相似于C,且C就是A的若当标准型。
所以B只有在A是不可逆的时候才存在。
将主对角元是0的若当块放在上面,组成的准对角阵记作B,而把主对角元不是0的若当块放在下面,组成的准对角阵为C。
复习题部分
23.设 是特征值为零的n阶Jordan块,求
是特征值为零的n阶Jordan块,求 的Jordan标准型。
的Jordan标准型。
解:和
的特征值式相同,都为零,
J是一个n次幂零矩阵,
所以J的极小多项式,
当n为偶数的时候,是一个
次幂零矩阵,
若n为奇数的时候,是一个
次幂零矩阵。(这里一定不能写成不是(n-1)/2!!)
24.求下列n阶矩阵的Jordan标准型:
这个矩阵的特征值为c,特征多项式是,则
,这个矩阵的秩为n-2,
所以该矩阵应该有两个若当块。
然后用公式判断有1个一阶若当块,则剩下的一定是一个n-1阶若当块。
可以得到若当标准型
29.设m阶矩阵A与n阶矩阵B没有公共的特征值,且A,B的Jordan标准型分别为 ,又C为mxn阶矩阵,求证:
,又C为mxn阶矩阵,求证: 的Jordan标准型为diag{
的Jordan标准型为diag{ }
}
(因为本题会用到35和36题的结论,所以建议先看一看这两个题)
假设你已经知道了35和36
那么存在X为非零解使得
AX-XB=C,所以有
接下来就是常规的分块矩阵相乘可以的得到Jordan标准型为mxn。
34.设A,B为n阶矩阵,满足AB=BA=0, ,求证
,求证 .
.
已知:,
下证
,
所以可知存在一个
35.设A,B分别是m,n阶矩阵,求证:矩阵方程AX=XB只有零解的充分必要条件是A,B无公共的特征值。
证:必要性:
设C是AX=XB的一个解,则
AC=CB,由数学归纳法得到,对任意的正整数k,都有,
将A和B带入任意一个相同的多项式,都有
如果这个多项式是A的特征多项式,此结论依然成立。所以可以得到,而
,所以得到了
,所以B的特征值为A的特征值。矛盾。
充分性:
反证,假设A B有公共的特征值,
(
是
的一个列向量)
则,,(
是
的列向量)(
是B的特征向量)
如果令
,又特征向量不为零,则出现了非零解,矛盾。
结语:这一篇写完让我觉得很多本来会的东西又不会了。而且我在这里致谢一下我的高等代数老师,她在休息中也依然为我解惑,得此良师,终生有幸。但是我恨期末周,没有细细检查,有错误欢迎指出呀。
