1 同余
1.
若\(a \equiv b \pmod m\),当且仅当\(m \mid (a - b)\)
2.同加性:
若\(a \equiv b \pmod m\),则\(a + c \equiv b + c \pmod m\)
3.同乘性:
若\(a \equiv b \pmod m\),则\(a * c \equiv b * c \pmod m\) 若\(a \equiv b \pmod m, c \equiv d \pmod m\),则\(a * c \equiv b * d \pmod m\)
4.
不满足同除性,但若\(gcd(c, m) = 1\),则当\(a * c \equiv b * c \pmod m\)时,有\(a \equiv b \pmod m\)
5.同幂性:
若\(a \equiv b \pmod m\),则\(a ^ n \equiv b ^ n \pmod m\)
6.推论1:
\(a * b \bmod k = (a \bmod k) * (b \bmod k) \bmod k\)
7.推论2:
若\(p, q\)互质,且\(a \bmod p = x\),\(a \bmod q = x\),则\(a \bmod (p * q) = x\)
2 素数
2.1 有关素数的定理
1.唯一分解定理:任何一个大于1的正整数都能被唯一分解为有限个素数的乘积,可写作:\(N = {p_1} ^ {c_1}{p_2} ^ {c _ 2} \cdots {p _ m} ^ {c _ m}\), 其中\({c_i}\)都是正整数,\({p _ i}\)都是素数且满足\({p_1} < {p_2} < \cdots <{p_m}\)
2.N中最多只能含有一个大于\(\sqrt{N}\)的因子
3.分解质因数:试除法:枚举\(2 \sim \sqrt{n}\),遇到质因子就除净并且记录质因子的个数。如果最后\(n > 1\),这就说明这就是大于\(\sqrt{n}\)的因子
int n, a[10001]; //质因子的个数
inline void decompose(int x) { //分解质因数
for (rg int i = 2; i * i <= x; i++) {
while (x % i == 0) {
a[i]++;
x /= i;
}
}
if (x > 1) a[x]++;
}
2.2 素数判定
1.按照素数的定义模拟
inline bool is_prime(int x) {
if (x == 0 || x == 1) return false;
for (rg int i = 2; i * i <= x; i++) {
if (x % i == 0) return false;
}
return true;
}
2.埃式筛法
int prime[N], cnt;
bool is_prime[N];
inline void Eratosthenes(int n) {
is_prime[0] = is_prime[1] = false;
for (rg int i = 2; i <= n; i++) {
is_prime[i] = true;
}
for (rg int i = 2; i <= n; i++) {
if (is_prime[i]) {
prime[++cnt] = i;
if ((long long)i * i > n) continue;
for (rg int j = i * i; j <= n; j += i) {
is_prime[j] = false;
}
}
}
}
3.线性筛法(欧拉筛法):每个合数只被它最小的质因子筛掉
int vis[N]; //划掉合数
int prime[N]; //记录质数
int cnt; //质数个数
inline void get_prime(int n) {
for (rg int i = 2; i <= n; i++) {
if (!vis[i]) prime[++cnt] = i; //如果当前数没被划掉,必定是质数,记录
for (rg int j = 1; 1ll * i * prime[j] <= n; j++) { //枚举已记录的质数,如果合数越界则中断
vis[i * prime[j]] = true; //划掉合数
if (i % prime[j] == 0) break; //控制每个合数只被它的最小素数因子筛掉一次
}
}
}
2.3 欧拉函数
1.定义:\(1 \sim n\)中与\(n\)互质的数的个数,用字母\(\varphi\)表示。
\(\varphi(n) = n \times \prod _ {i = 1} ^ {k} (1 - \frac{1}{p _ i})\),其中\(p_1, p_2, \cdots, p_k\)为n的所有质因数。
2.性质:
(1)\(\varphi(1) = 1\)。
(2)若p是素数,则\(\varphi(p) = p - 1\)。
(3)若p是素数,则\(\varphi(p ^ k) = (p - 1) \times p ^ {k - 1}\)。
(4)欧拉函数为积性函数:$\forall a, b \in N^* \(,且\)gcd(a, b) = 1\(,则\)\varphi(a \times b) = \varphi(a) \times \varphi(b)\(。特别的,对于奇数n,\)\varphi(2n) = \varphi(n)$
3.欧拉函数性质变形:
(1)p为素数,若n % p \(= 0\),则\(\varphi(n \times p) = p \times \varphi(n)\)。(\(n \times p\)的素数因子和n是一样的,所以用欧拉函数公式把\(\varphi(n \times p)\)展开)
(2)p为素数,若n % p \(\ne 0\),则\(\varphi(n \times p) = (p - 1) \times \varphi(n)\)。(n和p互质,满足积性函数)
(3)与n互质的数都是成对出现的,且每对的和为n,所以大于2的数的\(\varphi(n)\)都为偶数。
4.求欧拉函数:
(1)试除法:如果只要求一个数的欧拉函数值,那么直接根据定义,在质因数分解的同时求解
inline int euler_phi(int n) {
rg int ans = n;
for (rg int i = 2; i * i <= n; i++) {
if (n % i == 0) {
ans = ans / i * (i - 1);
while (n % i == 0) n /= i; //把这个因数除尽
}
}
if (n > 1) ans = ans / n * (n - 1);
return ans;
}
(2)筛法:在线性筛中,每一个合数都是被最小的质因子筛掉。比如设\(p_1\)是n的最小质因子,\(i = \frac{n}{p_1}\),那么线性筛的过程中n通过\(i \times p_1\)筛掉。
如果\(i \bmod p_1 = 0\),那么i包含了n的所有质因子:
\[\begin{aligned}\varphi(n) = n \times \prod_{i= 1}^s{\frac{p_i - 1}{p_i}} = p_1 \times i \times \prod_{i = 1}^s{\frac{p_i - 1}{p_i}}& = p_1 \times \varphi(i)\end{aligned} \]那如果\(i \bmod p_1 \ne 0\)呢,这时i和\(p_1\)是互质的,根据欧拉函数性质,我们有:
\(\begin{aligned}\varphi(n) & = \varphi(p_1) \times \varphi(i) = (p_1 - 1) \times \varphi(i) \end{aligned}\)
int p[N]; //存质数
int cnt;
int phi[N];
bool not_prime[N]; //存合数
inline void get_phi(int n) {
phi[1] = 1;
for (rg int i = 2; i <= n; i++) {
if (!not_prime[i]) { //是质数
p[++cnt] = i;
phi[i] = i - 1;
}
for (rg int j = 1; i * p[j] <= n; j++) {
rg int m = i * p[j];
not_prime[m] = 1; //标记为合数
if (i % p[j] == 0) {
phi[m] = p[j] * phi[i];
break;
} else {
phi[m] = (p[j] - 1) * phi[i];
}
}
}
}
2.4 线性筛求约数个数与约数和
1.约数个数:
用\(d_i\)表示i的约数个数,\(num_i\)表示i的最小质因子出现次数。
若\(n = \prod_{i = 1}^m {p_i} ^ {c_i}\),则\(d_i = \prod_ {i = 1}^m (c_i + 1)\)。
int prime[N], cnt;
bool not_prime[N];
int d[N]; //约数个数
int num[N]; //最小质因数的个数
int n;
inline void get_prime(int n) {
d[1] = 1;
for (rg int i = 2; i <= n; i++) {
if (!not_prime[i]) { //i是质数
prime[++cnt] = i;
d[i] = 2; //1和i
num[i] = 1; //i自己,共1个
}
for (rg int j = 1; i * prime[j] <= n; j++) {
rg int m = i * prime[j];
not_prime[m] = true;
if (i % prime[j] == 0) {
d[m] = d[i] / (num[i] + 1) * (num[i] + 2);
num[m] = num[i] + 1;
break;
} else {
d[m] = d[i] * 2;
num[m] = 1;
}
}
}
}
2.约数和:\(sd_i\)表示i的约数和,\(num_i\)表示最小质因子的\(p_0 + p_1 + \cdots + p_k\)。
\(sd_i = (p_1^0 + p_2^1 + \cdots + p_1^{r_1}) * (p_2^0 + p_2^1 + \cdots + p_2^{r_2}) * \cdots* (p_k^0 + p_k^1 + \cdots + p_k ^ {r _ k})= \prod_{i = 1}^k \sum_{j = 0}^{r_k} {p_i ^ j}\)
分治求等比数列的和:\(s = a^0 + a^1 + a^2 + \cdots + a^n\)
当n为奇数时:\(s = (1 + a^{\frac{n}{2} + 1}) * (a^0 + a^1 + \cdots + a^{\frac{n}{2}})\)
当n为偶数时:\(s = (1 + a^{\frac{n}{2} + 1}) * (a^0 + a^1 + \cdots + a^{\frac{n}{2} - 1}) + a^{\frac{n}{2}}\)
int prime[N], cnt;
bool not_prime[N];
int num[N];
int sd[N];
int n;
inline void get_primes(int n) {
sd[1] = 1;
for (rg int i = 2; i <= n; i++) {
if (!not_prime[i]) {
sd[i] = num[i] = i + 1;
prime[++cnt] = i;
}
for (rg int j = 1; i * prime[j] <= n; j++) {
rg int m = i * prime[j];
not_prime[m] = true;
if (i % prime[j]) {
sd[m] = sd[i] * sd[prime[j]]; //积性函数
num[m] = prime[j] + 1;
} else {
sd[m] = sd[i] / num[i] * (num[i] * prime[j] + 1);
num[m] = num[i] * prime[j] + 1;
break;
}
}
}
}
2.5 欧拉定理/费马小定理
1.费马小定理:若p为素数,\(\gcd(a, p) = 1\),则\(a^{p - 1} \equiv 1 \pmod p\)。
另:对于任意整数a,有\(a ^ p \equiv a \pmod p\)。
2.欧拉定理:若\(gcd(a, m) = 1\),则\(a^{\varphi(m)} \equiv 1 \pmod m\)。
3.扩展欧拉定理:
\(a^b \equiv \begin{cases} a^{b \bmod \varphi(m)}, &\gcd(a,m) = 1, \\ a^b, &\gcd(a,m)\ne 1, b < \varphi(m), \\ a^{(b \bmod \varphi(m)) + \varphi(m)}, &\gcd(a,m)\ne 1, b \ge \varphi(m). \end{cases} \pmod m\)
4.秦九昭算法:
\[\begin{aligned} f(x) &= a _ n x ^ n + a _ {n - 1} x ^ {n - 1} + \cdots + a _ 1 x + a_0 \\ &= (a_n x^{n - 1} + a_{n - 1} x^{n - 2} + \cdots + a_2 x + a_1)x + a_0 \\ &= ((a_n x ^ {n - 2} + a_{n - 1} x ^ {n - 3} + \cdots + a _ 3 x + a _ 2) x + a_1) x + a_0 \\ &\vdots \\ &= (\cdots((a_n x + a _ {n - 1}) x + a _ {n - 2} ) x + \cdots + a_1)x + a_0 \end{aligned} \]求多项式的值时,首先计算最内层括号内一次多项式的值,即:
\[\begin{aligned} v_0 = a_n \\ v_1 = a _ n &x + a _ {n - 1} \end{aligned} \]然后由内向外逐层计算一次多项式的值,即:
\[\begin{aligned} v_2 = v_1 x + a_{n - 1} \\ v_3 = v_2 x + a_{n - 3} \\ \vdots \\ v_n = v_{n - 1} x + a_0 \end{aligned} \]这样,求n次多项式\(f(x)\)的值就转化为求n个一次多项式的值。
3 最大公约数
3.1 欧几里得算法
1.辗转相除法:\(gcd(x, y) = gcd(y, x \% y)\)。
//递归形式
inline int gcd(int x, int y) {
return (y == 0 ? x : gcd(y, x % y));
}
//非递归形式
inline int gcd(int x, int y) {
rg int r = x % y;
while (r) {
x = y;
y = r;
r = x % y;
}
return y;
}
(速度:非递归 \(>\) 递归 \(>\) __gcd(),\(10^7\)数据下前两个差距不大,__gcd()慢0.1s左右)
2.最小公倍数:\(lcm(a, b) * gcd(a, b) = a * b\)
3.裴蜀定理(贝祖定理):设\(a, b\)为不全为0的整数,则\(\exists x, y\),使得:\(ax + by = gcd(a, b)\)。
4.裴蜀定理推广:
(1)一定存在整数x, y,满足\(ax + by = gcd(x, y) \times n\)。
(2)一定存在整数\(X_1 , X_2, \cdots , X_n\),满足\(\sum _ {i = 1} ^ n A_iX_i = gcd(A_1, A_2, \cdots , A_n)\)。
3.2 扩展欧几里得
1.作用:求\(ax + by = gcd(a, b)\)的一组整数解。
2.证明:
\(ax_1 + by_1 = gcd(a, b)\)
\(bx_2 + (a \% b)y_2 = gcd(b, a \% b)\)
\(\because gcd(a, b) = gcd(b, a \% b)\)
\(\therefore ax_1 + by_1 = bx_2 + (a \% b)y_2\)
\(\because a \% b = a - \lfloor \frac a b \rfloor \times b\)
\(\therefore ax_1 + by_1 = bx_2 + (a - \lfloor \frac a b \rfloor \times b)y_2 = ay_2 + b(x_2 - \lfloor \frac a b \rfloor y_2)\)
因为系数相同,所以我们可以让\(x_1 = y_2\),\(y_1 = x_2 - \lfloor \frac a b \rfloor y_2\)
显然,可以利用递归,先求出下一层的解\(x_2\),\(y_2\),再回到上一层,求出特解\((x_1, y_1)\),顺便求出\(gcd(a, b)\)。
//求解 ax+by = gcd(a,b)
//返回gcd(a,b)的值
inline int exgcd(int a, int b, int &x, int &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
int ret = exgcd(b, a % b, x, y);
int t = x;
x = y;
y = t - a / b * y;
return ret;
}
3.构造通解:
\[\begin{cases}x = x_0 + \frac b {gcd(a, b)} \times k \\ y = y_0 - \frac a {gcd(a, b)} \times k\end{cases} \]4.求不定方程\(ax + by = c\)的一组整数解:
若\(gcd(a, b) | c\),则有整数解。先用扩欧求得\(ax+by = gcd(a, b)\)的解,再乘以\(\frac c {gcd(a, b)}\),即原方程的特解。
若\(gcd(a, b) \nmid c\),则无整数解。
inline int exgcd(int a, int b, int &x, int &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
rg int ret = exgcd(b, a % b, x, y);
rg int t = x;
x = y;
y = t - a / b * y;
return ret;
}
int main() {
int a, b, c, x, y;
cin >> a >> b >> c;
rg int d = exgcd(a, b, x, y);
if (c % d == 0) {
cout << c / d * x << " " << c / d * y << "\n";
} else {
cout << "none" << "\n";
}
return qwq;
}
5.扩欧求解线性同余方程:
(1)把同余方程转化为不定方程:由\(ax \equiv b \pmod m\)得\(ax = -my + b\),即\(ax + my = b\),由裴蜀定理得,当\(gcd(a, m) \mid b\)时有解
(2)扩欧求\(ax + my = gcd(a, m)\)的解,之后把x乘以\(\frac b {gcd(a, m)}\),即原始方程的特解。
(3)x的最小整数解:\(x = (x \% m + m) \% m\)
4 乘法逆元
4.1 定义
如果一个线性同余方程\(ax \equiv 1 \pmod b\),则称x为a在模b意义下的乘法逆元,记作\(a^{-1}\)。
并非所有情况下都存在乘法逆元,但当\(gcd(a, b) = 1\),即a,b互质时,存在乘法逆元。
4.2 逆元的用途
因为对于除法取模不成立,即\((a \div b) \% p \ne ((a \% p) \div (b \% p)) \% p\),所以用逆元来解决这个问题。
逆元就是把除法取模运算转化为乘法取模运算。
对于\((a \div b) \% p = m\),假设存在一个数x满足\((a \times x) \% p = m\),两边同乘b得到:\(a \% p = (m \times (b \% p)) \% p\);若a和b均小于p的话,上式改为:\(a = (m \times b) \% p\),等式两边同时乘以x,联立(2)式得到:\((a \times x) \% p = (x \times m \times b) \% p = (x \times m \times b) \% p\),因此可以得到:\((b \times x) \% p = 1\)。可以看出x是b在模p意义下的逆元。
由以上过程我们看到,求\((a \div b) \% p\) 等同于求$a \times (b $ 的逆元 \() \% p\)。因此求模运算的除法问题就转化为求一个数的逆元问题了。
4.3 如何求乘法逆元
1.费马小定理(模数为素数且\(p \nmid a\))
因为 \(ax \equiv 1 \pmod p\)
所以 \(ax \equiv a^{p-1} \pmod p\)
所以 \(x \equiv a^{p-2} \pmod p\)
inline ll quickpow(ll a, ll n, ll p) { //求 a ^ n % p
ll ans = 1;
while (n) {
if (n & 1) ans = ans * a % p;
a = a * a % p;
n >>= 1;
}
return ans;
}
inline ll niyuan(ll a, ll p) { //求 a ^ (p - 2) % p
return quickpow(a, p - 2, p);
}
2.欧拉定理求逆元(a与p互质)
若 \(gcd(a, p) = 1\),则\(a^{\varphi (p)} \equiv 1 \pmod p\)。
那么\(a^{\varphi(p) - 1}\)即为a在模p意义下的逆元。
inline ll inv(ll a, ll p) {
ll phi = p, mod = p;
for (rg int i = 2; i * i <= p; i++) {
if (p % i == 0) {
phi = phi / i * (i - 1);
while (p % i == 0) p /= i;
}
}
if (p > 1) phi = phi / p * (p - 1);
phi--;
ll res = 1, t = a;
while (phi) {
if (phi & 1) res = (res * t) % mod;
t = (t * t) % mod;
phi >>= 1;
}
return res;
}
3.扩展欧几里得求逆元(a与p互质)
我们将\(ax \equiv 1 \pmod p\)转换成\(ax = p(-y) + 1\),移项得 \(ax + py = 1\),可用扩欧求解,逆元为
\((res \% p + p) \% p\)。
inline ll exgcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
rg ll res = exgcd(b, a % b, x, y);
rg ll t = x;
x = y;
y = t - a / b * y;
return res;
}
4.线性求逆元 (模数为质数)
首先,\(1^{-1} \equiv 1 \pmod p\)。设\(p = k \times i + r\),其中\(1 < i < p, r < i\),再放到模p意义下,则有:\(k \times i + r \equiv 0 \pmod p\)。两边同时乘以\(i^{-1} \times r^{-1}\),则:
\[\begin{aligned} k \times i \times i^{-1} \times r^{-1} + r \times i^{-1} \times r^{-1} \equiv 0 \pmod p \\\ k \times r^{-1} + i^{-1} \equiv 0 \pmod p \\\ i^{-1} \equiv -k \times r ^ {-1} \pmod p \\\ i^{-1} \equiv -\lfloor \frac p i \rfloor \times r^{-1} \pmod p \\\ i^{-1} \equiv -\lfloor \frac p i \rfloor \times (p \bmod i) ^ {-1} \pmod p\end{aligned} \]设\(t = \frac p i, k = p \% i\),有:\(p = i \times t + k\),即$i \times t + k \equiv 0 \pmod p \(,即\)k \equiv -i \times t \pmod p\(。两边同时除以\)i \times k\(,有\)\frac 1 i \equiv -\frac t k \pmod p\(,将k,t带入有\)inv[i] \equiv -\frac p i \times inv[p % i] \pmod p\(,为防止有负数,有\)inv[i] = (p - \frac p i) \times inv[p % i]) % p$。
ll ny[MAXN];
inline void get_inv(int n, int p) {
ny[1] = 1;
for (rg int i = 2; i <= n; i++) {
ny[i] = (ll)(p - p / i) * ny[p % i] % p;
}
}
4.4 补充
1.逆元是(完全)积性函数,所以在求\(2 ^ m x \equiv 1 \pmod b\)时可以直接求出2在\(\bmod b\)意义下的逆元,这个数的m次方\(\bmod b\)就是\(2^m\)在\(\bmod b\)意义下的逆元。
5 计数原理
1.加法原理:
完成一件事情共有n类方法,第一类方法有\(n_1\)种方案,第二类有\(n_2\)种方案\(\cdots\)那么完成这件事情共有\(n_1 + n_2 + \cdots\)种方法,注意分类需要不重不漏。
2.乘法原理:
完成一件事情需要分成n步进行,第一步有\(n_1\)种方法,第二步有\(n_2\)种方法\(\cdots\)那么完成这件事共有\(n_1 * n_2 * \cdots\)种方法。
3.排列与组合
(1)排列:从n个元素中取出m个元素进行排序,用符号\(A_n^m\)表示。
\(A(n, m)=n * (n-1) * (n-2) * \cdots * (n - m + 1) = \frac {n!} {(n-m)!}\)
(2)组合:从n个元素中仅仅取出m个元素,不考虑排序,用符号\(C_n^m\)表示。
\(C(n, m) = A(n, m) / A(m, m) = \frac {n!} {m!(n-m)!}\)
4.常用策略方法
(1)特殊元素和特殊位置优先策略
(2)相邻元素捆绑策略
(3)不相邻问题插空策略
(4)定序问题倍缩空位插入策略
例:7人排队,其中甲乙丙3人顺序一定,共有多少不同的排法?
共有\(\frac {A(7, 7)}{A(3,3)}\)。
(5)排列问题求幂策略
(6)环排问题线排策略
(7)多排问题直排策略
(8)排列组合混合问题先选后排策略
(9)平均分组问题除法策略
(10)重排列
(11)错位排序
错排问题指一个有n个元素的排列,如若一个排列使得所有的元素不在原来的位置上,则称这个排列为原排列的一个错排。
用\(D(n)\)表示n个元素的排列的错排数。
\(D(n)=(n-1)* (D(n-1)+D(n-2))\)。
特殊地,\(D(1)=0,D(2)=1\)。
6 组合数取模
6.1 求组合数
1.递推法:
有q\((q \le 10000)\)组询问,每组询问两个整数n,m\((1 \le m \le n \le 2000)\),求\(C_{n} ^ {m} \bmod (10 ^ 9 + 7)\)。
递推式:\(C_{n} ^ {m} = C_{n - 1} ^ {m} + C_{n - 1} ^ {m - 1}\)
从n个不同数中选出m个不同方案数是\(C_{n} ^ {m}\),对第1个数有选和不选两种决策:若不选,则从剩下的\(n -1\)中选m个,即\(C_{n - 1} ^ {m}\)。若选,则从剩下的\(n - 1\)中选\(m - 1\)个,即\(C_{n - 1} ^ {m - 1}\)。
const int N = 2010, mod = 1e9 + 7;
int c[N][N];
inline void init() {
for (rg int i = 0; i < N; i++) {
c[i][0] = 1;
}
for (rg int i = 1; i < N; i++) {
for (rg int j = 1; j <= i; j++) {
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
}
}

2.计算法:
有q\((q \le 10000)\)组询问,每组询问两个整数n,m\((1 \le m \le n \le 10^5)\),求\(C_{n} ^ {m} \bmod (10 ^ 9 + 7)\)。
用\(C_{n} ^ {m} = \frac {n!} {(n - m)!m!}\)直接计算。
开两个数组分别存模意义下的阶乘和阶乘的逆元。
用\(f[x]\)存\(x!\bmod p\)的值。
用\(g[x]\)存\((x!)^{-1} \bmod p\)的值
根据费马小定理\(a \times a ^ {p - 2} \equiv 1 \pmod p\),可以用快速幂求逆元:
\(C _ n ^ m \pmod p = f[n] \times g[n - m] \times g[m] \pmod p\)
ll f[N], g[N];
inline ll qpow(ll a, int b) {
rg ll res = 1;
while (b) {
if (b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
inline void init() {
f[0] = g[0] = 1;
for (rg int i = 1; i < N; i++) {
f[i] = f[i - 1] * i % mod;
g[i] = g[i - 1] * qpow(i, mod - 2) % mod;
}
}
inline ll C(ll n, ll m) {
return f[n] * g[m] % mod * g[n - m] % mod;
}
另:
计算出每一个逆元的值有些浪费时间,可以在需要时再求,因此有代码:
inline void init() {
f[0] = 1;
for (rg int i = 1; i < N; i++) {
f[i] = f[i - 1] * i % mod;
}
}
inline ll C(ll n, ll m) {
return f[n] * qpow(f[m], mod - 2) % mod * qpow(f[n - m], mod - 2) % mod;
}
对lucas也同样适用。
求逆元也可以递推:阶乘的逆元
\(\frac 1 {i!} \pmod p = \frac 1 i \times \frac 1 {(i - 1)!} \pmod p = pow(i, p - 2) \times g[i - 1] \pmod p\)
6.2 大组合数取模(Lucas定理)
1.给定整数n,m,p的值,求\(C _ n ^ m \pmod p\)的值。其中\(1 \le m \le n \le 10^{18}\),\(1 \le p \le 10 ^ 5\),保证p为素数。
2.求解:
对于质数p,有:
\(C _ n ^ m \equiv C _ {\frac n p} ^ {\frac m p} \times C _ {n \bmod p} ^ {m \bmod p} \pmod p\)
上式中,\(n \bmod p\)和\(m \bmod p\)一定小于p,可以直接求解,\(C _ {\frac n p} ^ {\frac m p}\)可以继续用Lucas定理求解。这也就要求p的范围不能够太大,一般在\(10^5\)左右。边界条件:当\(m = 0\)时,返回1。
3.引理
(1)\(C _ p ^ x \equiv 0 \pmod p\)。\((0 < x < p)\)
(2)\((1 + x)^p \equiv 1 + x ^ p \pmod p\)
//模版
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
const int N = 100010;
ll f[N], g[N];
ll p;
inline ll qpow(ll a, ll b, ll p) {
rg ll res = 1;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
inline void init() {
f[0] = g[0] = 1;
for (rg int i = 1; i <= p; i++) {
f[i] = f[i - 1] * i % p;
g[i] = g[i - 1] * qpow(i, p - 2, p) % p;
}
}
inline ll C(ll n, ll m) {
if (n < m) return 0;
return f[n] * g[m] * g[n - m] % p;
}
inline ll lucas(ll n, ll m) {
if (m == 0) return 1;
return lucas(n / p, m / p) * C(n % p, m % p) % p;
}
ll q, n, m;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> q;
while (q--) {
cin >> n >> m >> p;
init();
cout << lucas(n + m, n) << "\n";
}
return qwq;
}
7 中国剩余定理(CRT)
7.1 简介
「物不知数」问题:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
中国剩余定理可求解如下形式的一元线性同余方程组。
\[\begin{cases} x \equiv r_1 \pmod {m_1} \\ x \equiv r_2 \pmod {m_2} \\ \vdots \\ x \equiv a_k \pmod {n_k} \end{cases} \]求x的最小非负整数解。(其中模数\(m_1, m_2, \cdots m_k\)为两两互质整数)
7.2 过程
1.计算所有模数的乘积\(M = m_1 \times m_2 \times m_3 \times \cdots \times m_n\);
2.对于第i个方程:
a.计算\(c_i = \frac M {m_i}\)
b.计算\(c_i\)在模\(m_i\)意义下的逆元\(c_i ^ {-1}\)。(逆元一定存在,因为\(c_i\)中已经把\(m_i\)除掉了)
3.方程组的唯一解为:\(x = \sum _ {i = 1} ^ n r_i c_i c_i^{-1} \bmod M\)。
例:
\[\begin{cases} x \equiv 2 \pmod 3 \\ x \equiv 3 \pmod 4 \\ x \equiv 1 \pmod 5 \end{cases} \]1.\(M = 3 \times 4 \times5 = 60\)
2.\(c_1 = 20\),\(c_1 ^ {-1} = 2\)
\(c_2 = 15\),\(c_2^{-1} = 3\)
\(c_3 = 12\),\(c_3^{-1} = 3\)
3.\(x = (2 \times 20 \times 2 + 3 \times 15 \times + 1 \times 12 \times 3) \% 60 = 11\)
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
ll n, a[11], b[11];
inline ll exgcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
rg ll ret = exgcd(b, a % b, x, y);
rg ll t = x;
x = y;
y = t - a / b * y;
return ret; //x就是逆元
}
inline ll CRT(ll m[], ll r[]) {
ll M = 1, ans = 0;
for (rg int i = 1; i <= n; i++) M *= m[i];
for (rg int i = 1; i <= n; i++) {
rg ll c = M / m[i], x, y;
exgcd(c, m[i], x, y);
ans = (ans + r[i] * c * x % M) % M;
}
return (ans % M + M) % M;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for (rg int i = 1; i <= n; i++) {
cin >> a[i] >> b[i];
}
cout << CRT(a, b) << "\n";
return qwq;
}
7.3 扩展卢卡斯定理
Lucas定理中要求模数p必须为素数,那么对于p不是素数的情况,就要用到exLucas。
1.题目:(P4720 【模板】扩展卢卡斯定理/exLucas)
求 \(C _ n ^ m \bmod P\)。
2.过程:
(1)第一部分:中国剩余定理
考虑利用中国剩余定理合并答案。
根据唯一分解定理,将P质因数分解:
\(P = p_1^{a_1} \times p_2^{a_2} \times \cdots \times p_r^{a_r} = \prod_{i = 1}^{r} p_i^{a_i}\)
对于任意i,j,有 \(p_i^{a_i}\) 与 \(p_j^{a_j}\) 互质,所以可以构造出如下r个同余方程:
\[\begin{cases} a_1 \equiv C_m^n \pmod {p_1^{a_1}} \\ a_2 \equiv C_m^n \pmod {p_2^{a_2}} \\ \vdots \\ a_r \equiv C_m^n \pmod {p_r^{a_r}} \end{cases} \](2)第二部分:移除分子分母中的素数
根据同余的定义,\(a_i = C_m^n \bmod p_i^{a_i}\),问题转化成,求\(C_m^n \bmod p^a\)(p为质数)的值。
根据组合数定义,\(C_m^n \bmod p^a = \frac {n!} {m!(n-m)!} \bmod p^a\)。
由于式子是在模\(p^a\)意义下,所以分母要算乘法逆元。
同余方程\(ax \equiv 1 \pmod p\)(即乘法逆元)有解的充要条件为\(\gcd(a,p) = 1\),然而无法保证有解,发现无法直接求\(inv_{m!}\)和\(inv_{(n-m)!}\),所以将原式转化为:
\(\frac{\frac{n!}{p^x}}{\frac{m!}{p^y}\frac{(n-m)!}{p^z}}p^{x-y-z} \bmod p^a\)
x表示n!中包含多少个p因子,y,z同理。
(3)第三部分:Wilson定理的推论
问题转化成,求形如:\(\frac {n!} {q^x} \bmod q^k\)的值。这时可以利用Wilson定理的推论。
解释:
一个示例:\(22!\bmod 3^2\)
\(22! = 3^7 \times (1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7) \times (1 \times 2 \times 4 \times 5 \times 7 \times 8 \times 10 \times 11 \times 13 \times 14 \times 16 \times 17 \times 20 \times 22)\)
可以看到,式子分为三个整式的乘积:
1> 是\(q^{\lfloor \frac {n}{q} \rfloor}\);
2> 是\(\lfloor \frac n q \rfloor!\),由于阶乘中仍然有可能有q的倍数,考虑递归求解;
3> 是\(n!\)中与q互质的部分的乘积,具有如下性质:
\(1 \times 2 \times 4 \times 5 \times 7 \times 8 \equiv 10 \times 11 \times 13 \times 14 \times 16 \times 17 \pmod {3^2}\),即:
\(\displaystyle \prod_{i,\gcd(i,q)=1}^{q^k}i\equiv\prod_{i,\gcd(i,q)=1}^{q^k}(i+tq^k) \pmod{q^k}\)(t是任意正整数)。
\(\displaystyle \prod_{i,\gcd(i,q)=1}^{q^k}i\) 一共循环了\(\displaystyle \lfloor\frac{n}{q^k}\rfloor\) 次,暴力求出\(\displaystyle \prod_{i,\gcd(i,q)=1}^{q^k}i\),然后用快速幂求\(\displaystyle \lfloor\frac{n}{q^k}\rfloor\) 次幂。
最后要乘上\(\displaystyle \prod_{i,\gcd(i,q)=1}^{n \bmod q^k}i\),即 \(19\times 20\times 22\),显然长度小于 q^k,暴力乘上去。
上述三部分乘积为\(n!\)。最终要求的是\(\frac{n!}{q^x} \bmod {q^k}\)。
所以有:\(n! = q^{\lfloor \frac n q \rfloor} \times (\lfloor \frac n q \rfloor)! \times (\displaystyle \prod _ {i, \gcd(i,q) = 1} ^ {q^k}i)^{\lfloor \frac{n} {q^k} \rfloor} \times (\prod _ {i, \gcd(i,q) = 1} ^ {n \bmod q^k}i)\)
于是:
\(\frac{n!}{q^{\lfloor \frac n q \rfloor}} = (\lfloor \frac n q \rfloor)! \times (\displaystyle \prod _ {i, \gcd(i,q) = 1} ^ {q^k}i)^{\lfloor \frac{n} {q^k} \rfloor} \times (\prod _ {i, \gcd(i,q) = 1} ^ {n \bmod q^k}i)\)
\((\lfloor \frac{n}{q} \rfloor)!\)同样是一个阶乘,所以也可以分为上述三个部分,于是可以递归求解。
等式的右边两项不含素数 q。事实上,如果直接把 n 的阶乘中所有 q 的幂都拿出来,等式右边的阶乘也照做,这个等式可以直接写成:
\(\frac{n!}{q^{x}} = \frac{\left(\left\lfloor\frac{n}{q}\right\rfloor\right)!}{q^{x'}} \cdot {\left(\prod_{i,\gcd(i,q)=1}^{q^k}i\right)}^{\left\lfloor\frac{n}{q^k}\right\rfloor} \cdot \left(\prod_{i,\gcd(i,q)=1}^{n\bmod q^k}i\right)\)
式中的 x 和 x' 都表示把分子中所有的素数 q 都拿出来。改写成这样,每一项就完全不含 q 了。
递归的结果,三个部分中,左边部分随着递归结束而自然消失,中间部分可以利用 Wilson 定理的推论 0,右边部分就是推论 2 中的 \(\prod_{j\geq 0}(N_j!) _ p\)。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
inline void exgcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1;
y = 0;
return ;
}
exgcd(b, a % b, x, y);
rg ll t = x;
x = y;
y = t - a / b * y;
}
inline ll gcd(ll a, ll b) {
if (b == 0) return a;
return gcd(b, a % b);
}
inline ll inv(ll a, ll p) {
rg ll x, y;
exgcd(a, p, x, y);
return (x + p) % p;
}
inline ll lcm(ll a, ll b) {
return a / gcd(a, b) * b;
}
inline ll mabs(ll x) {
return (x > 0 ? x : -x);
}
inline ll qmul(ll a, ll b, ll p) {
rg ll ret = 0;
a %= p;
b %= p;
while (b) {
if (b & 1ll) ret = (ret + a) % p;
b >>= 1ll;
a = (a + a) % p;
}
return ret;
}
inline ll qpow(ll a, ll b, ll p) {
rg ll ret = 1;
a %= p;
while (b) {
if (b & 1ll) ret = ret * a % p;
a = a * a % p;
b >>= 1ll;
}
return ret;
}
inline ll F(ll n, ll P, ll PK) {
if (n == 0) return 1;
rg ll rou = 1; //循环节
rg ll rem = 1; //余项
for (rg ll i = 1; i <= PK; i++) {
if (i % P) rou = rou * i % PK;
}
rou = qpow(rou, n/ PK, PK);
for (rg ll i = PK * (n / PK); i <= n; i++) {
if (i % P) rem = rem * (i % PK) % PK;
}
return F(n / P, P, PK) * rou % PK * rem % PK;
}
inline ll G(ll n, ll P) {
if (n < P) return 0;
return G(n / P, P) + n / P;
}
inline ll C_PK(ll n, ll m, ll P, ll PK) {
rg ll fz = F(n, P, PK), fm1 = inv(F(m, P, PK), PK), fm2 = inv(F(n - m, P, PK), PK);
rg ll mi = qpow(P, G(n, P) - G(m, P) - G(n - m, P), PK);
return fz * fm1 % PK * fm2 % PK * mi % PK;
}
ll A[1005], B[1005];
inline ll exlucas(ll n, ll m, ll P) {
rg ll ljc = P, tot = 0;
for (rg ll i = 2; i * i <= P; i++) {
if (ljc % i == 0) {
rg ll PK = 1;
while (ljc % i == 0) {
PK *= i;
ljc /= i;
}
A[++tot] = PK;
B[tot] = C_PK(n, m, i, PK);
}
}
if (ljc != 1) {
A[++tot] = ljc;
B[tot] = C_PK(n, m, ljc, ljc);
}
rg ll ans = 0;
for (rg int i = 1; i <= tot; i++) {
rg ll M = P / A[i], T = inv(M, A[i]);
ans = (ans + B[i] * M % P * T % P) % P;
}
return ans;
}
ll n, m, P;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m >> P;
cout << exlucas(n, m, P) << "\n";
return 0;
}
7.4 扩展中国剩余定理
1.问题:求解线性同余方程组
\[\begin{cases} x \equiv r_1 \pmod {m_1} \\ x \equiv r_2 \pmod {m_2} \\ \vdots \\ x \equiv a_k \pmod {n_k} \end{cases} \]求x的最小非负整数解。(其中模数\(m_1, m_2, \cdots m_n\)为不一定两两互质的整数)
2.思路:
前两个方程:\(x \equiv r_1 \pmod m_1\),\(x \equiv r_2 \pmod m_2\)
转化为不定方程:\(x = m_1 p + r1 = m_2 q + r_2\),则:\(m_1p - m_2q = r_2 - r_1\)。
由裴蜀定理,
当\(\gcd(m_1, m_2) \nmid (r_2 - r_1)\)时,无解
当\(\gcd(m_1, m_2) \mid (r_2 - r_1)\)时,有解
由扩欧算法,
得特解 \(p = p \times \frac{r_2 - r_1} {gcd}\),\(q = q \times \frac{r_2 - r_1} {gcd}\)
其通解 \(P = p + \frac {m_2} {gcd} \times k\),\(Q = q - \frac{m_1} {gcd} \times k\)
所以\(x = m_1P + r_1 = \frac{m_1 m_2} {gcd} \times k + m_1 p + r_1\)
前两个方程等价合并为一个方程\(x \equiv r \pmod m\),其中\(r = m_1p + r_1\),\(m = lcm(m_1, m_1)\)
所以n个同余方程只要合并\(n - 1\)次,即可求解。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef __int128 ll;
const int N = 100005;
ll n, m[N], r[N];
inline ll exgcd(ll a, ll b, ll &x, ll &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
rg ll ret = exgcd(b, a % b, x, y);
rg ll t = x;
x = y;
y = t - a / b * y;
return ret;
}
inline ll EXCRT(ll m[], ll r[]) {
rg ll m1, m2, r1, r2, p, q;
m1 = m[1], r1 = r[1];
for (rg int i = 2; i <= n; i++) {
m2 = m[i];
r2 = r[i];
rg ll d = exgcd(m1, m2, p, q); //d = gcd(m1, m2)
if ((r2 - r1) % d) return -1;
p = p * (r2 - r1) / d; //特解
p = (p % (m2 / d) + m2 / d) % (m2 / d); //因为p可能小于0,变成最小正整数
r1 = m1 * p + r1;
m1 = m1 * m2 / d;
}
return (r1 % m1 + m1) % m1;
}
int main() {
scanf("%lld", &n);
for (rg int i = 1; i <= n; i++) {
scanf("%lld%lld", m + i, r + i);
}
printf("%lld\n", EXCRT(m, r));
return qwq;
}
8 容斥原理
8.1 集合的并
1.\(A_1, A_2,\cdots ,A_n\)是n个集合,则这n个集合并集的元素个数是:
\(\left| \bigcup_{i=1}^{n}A_i\right| =\sum_{i = 1} ^n |A_i|-\sum_{i<j}|A_i\cap A_j|+\sum_{i<j<k}|A_i\cap A_j\cap A_k|-\cdots +(-1)^{n-1}|A_1\cap A_2 \cap \cdots\cap A_n|\)
解析:
\(\sum _ {i = 1} ^ n |A_i|\):将每个集合中的元素个数相加,该值大于总元素数,需修正;(系数为\((-1)^0\))
\(\sum _ {i < j} |A_i \cap A_j|\):减去两两相交的元素个数,该值小于总元素数,需修正;(系数为\((-1)^1\))
\(\sum _ {i < j < k} |A_i \cap A_j \cap A_k|\):加上三个集合相交的元素个数,该值大于总元素数,需修正;(系数为\((-1)^2\))
\(\vdots\)
\((-1)^{n - 1} |A_1 \cap A_2 \cap \cdots \cap A_n|\):加上\((-1)^{n - 1}\)乘以\(n - 1\)个集合相交的元素个数;(系数为\((-1)^{n - 1}\))
上述 奇数个集合的交集的元素个数前系数是正数,偶数个集合的交集的元素个数前系数是负数。
2.例题:给定一个整数n和m个不同的质数\(p_1, p_2, \cdots , p_m\)。求:\(1 \sim n\)中能被\(p_1, p_2, \cdots , p_m\)中的至少一个数整除的整数有多少个。
(1)交集的大小等于n除以质数的乘积。即\(|S_1| = \frac n {p_1}\),\(|S_1 \cap S_2| = \frac n {p_1 \times p_2}\),\(|S_1 \cap S_2 \cap S_3| = \frac n {p_1 \times p_2 \times p_3}\)。
(2)使用的二进制位来表示每个集合选与不选的状态。
如 若有3个质数,就需要3个二进制位来表示所有状态。
\(001 \to S_1,010\to S_2, 100\to S_3\),\(011\to S_1\cap S_2,101\to S_1\cap S_3,110\to S_2\cap S_3\),\(111\to S_1 \cap S_2 \cap S_3\)
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
const int N = 20;
int n, m, prim[N];
inline int calc() {
rg int res = 0;
for (rg int i = 1; i < 1 << m; i++) {
rg int t = 1, sign = -1;
for (rg int j = 0; j < m; j++) {
if (i & 1 << j) {
if ((ll)t * prim[j] > n) {
t = 0;
break;
}
t *= prim[j];
sign = -sign;
}
}
if (t) res += n / t * sign;
}
return res;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n >> m;
for (rg int i = 0; i < m; i++) {
cin >> prim[i];
}
cout << calc();
return qwq;
}
8.2 集合的交
集合的交等于全集减去补集的并
\(| \bigcap_{i=1}^{n} S_i| = |U| - |\bigcup_{i=1}^ {n}\overline{S_i}|\)
右边的补集的并使用容斥原理求解。

9 卡特兰数
9.1 介绍
卡特兰数是组合数学中一个常出现于各种计数问题中的数列。其前几项为(从第零项开始):\(1,1,2,5,14,42,132,429,1430,4862,\cdots\)
卡特兰数\(C[n]\)满足以下递推关系:
\(C[n] = C[0]C[n-1]+C[1]C[n-2]+\cdots+C[n-1]C[0]\)。
9.2 例
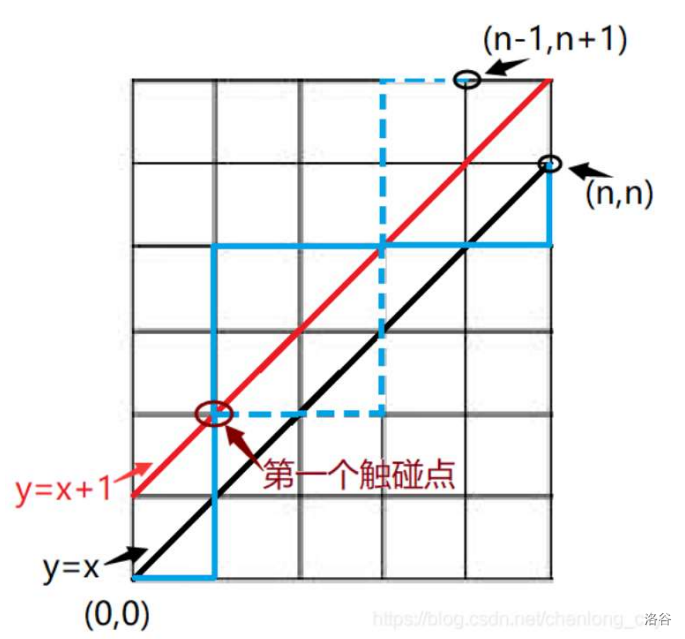
以走网格为例,从格点(0,0)走到格点(n,n),只能向右或向上走,并且不能越过对角线的路径的条数,就是卡特兰数,记为\(H_n\)。
1.通项公式:
(1)\(H_n = C_{2n}^n - C_{2n}^{n-1}\)
(2)\(H_n = \frac{1}{n+1} C_{2n}^n\)
(3)\(H_n = \frac{4n-2}{n+1}H_{n-1}\)
2.证明:
(1)证明(1)式:
先求路径总数,在2n次移动中选n次向右移动,即\(C_{2n}^n\)。
再求非法路径,即越过对角线\(y=x\)的路径。如果跨越了\(y=x\)那么一定触碰了\(y=x+1\)。
所有的非法路径与这一条线有至少一个交点,把第一个交点设为(a,a+1),把(a,a+1)之后的路径全部按照\(y=x+1\)这条线对称过去,这样,最后的终点就会变成(n-1,n+1)。
所有的非法路径对称后都唯一对应着一条到(n-1,n+1)的路径,所以非法路径数就是\(C_{2n}^{n-1}\),合法路径数就是\(C_{2n}^n - C_{2n}^{n-1}\)。
(2)证明(2)式:
\(H_n = C_{2n}^{n}-C_{2n}^{n-1} = \frac{(2n)!}{n!n!}-\frac{(2n)!}{(n+1)!(n-1)!}=\frac{(2n)!}{n!(n-1)!}(\frac{1}{n}-\frac{1}{n+1})=\frac{(2n)!}{n!n!(n+1)}=\frac{1}{n+1}C_{2n}{n}\)
9.3 应用
1.n个元素进栈序列为:\(1,2,3, \cdots ,n\),则有多少种出栈序列。
我们将进栈表示为+1,出栈表示为-1,则1 3 2的出栈序列可以表示为:+1,-1,+1,+1,-1,-1。
根据栈本身的特点,每次出栈的时候,必定之前有元素入栈,即对于每个-1前面都有一个+1相对应。因此,出栈序列的所有前缀和必然大于等于0,并且+1的数量等于-1的数量。
观察一下n=3的一种出栈序列:+1,-1,-1,+1,-1,+1。序列前三项和小于0,显然这是个非法的序列。如果将第一个前缀和小于0的前缀,即前三项元素都进行取反,就会得到:-1,+1,+1,+1,-1,+1。此时有3+1个+1以及3-1个-1。
因为这个小于0的前缀和必然是-1,且-1比+1多一个,取反后,-1比+1少一个,则+1变为n+1个,且-1变为n-1个。进一步推广,对于n元素的每种非法出栈序列,都会对应一个含有n+1个+1以及n-1个-1的序列。
假设非法序列为A,对应的序列为B。每个A只有一个“第一个前缀和小于0的前缀”,所以每个A只能产生一个B。而每个B想要还原到A,就需要找到“第一个前缀和大于0的前缀”,显然B也只能产生一个A。
每个B都有n+1个+1以及n-1个-1,因此B的数量为\(C_{2n}^{n+1}\),相当于在长度为2n的序列中找到n+1个位置存放+1。相应的,非法序列的数量也就等于\(C_{2n}^{n+1}\)。
出栈序列的总数量共有\(C_{2n}^{n}\),因此,合法的出栈序列的数量为\(C_{2n}^n-C_{2n}^{n+1}=\frac{1}{n+1}C_{2n}^n\)。
2.n对括号,则有多少种“括号匹配”的括号序列。
n对括号相当于有2n个符号,n个左括号、n个右括号,可以设问题的解为f(2n)。第0个符号肯定为左括号,与之匹配的右括号必须为1第2i+1个字符。
于是得到递推式:\(f(2n)=f(0) \times f(2n-2) + f(2) \times f(2n-4) + \cdots +f(2n-2) \times f(0)\)。
假设\(f(0)=1\),计算一下开始几项,\(f(2)=1,f(4)=2,f(6)=5\)。结合递推式,不难发现f(2n)等于h(n)。
3.n个节点构成的二叉树,共有多少种情形?
首先,根肯定会占用一个结点,那么剩余的n-1个结点可以有如下的分配方式:\((0,n-1),(1,n-2),\cdots ,(n-1,0)\),其中(i,j)表示根的左子树含i个结点,右子树含j个结点。
于是\(f(n)=f(0) \times f(n-1) + f(1) \times f(n-2)+ \cdots + f(n-1) \times f(0)\)。
假设f(0)=1,那么\(f(1)=1,f(2)=2,f(3)=5\)。结合递推式,不难发现f(n)等于h(n)。
4.求一个凸多边形区域划分成三角形区域的方法数。
以凸多边形的一边为基,设这条边的2个顶点为A和B。从剩余顶点中选1个,可以将凸多边形分成三个部分,中间是一个三角形,然后求解左右两个凸多边形。
设n个顶点的凸多边形的解为f(n),于是\(f(n)=f(2) \times f(n-1) + f(3) \times f(n-2) + \cdots + f(n-1) \times f(2)\)。
\(f(2) \times f(n-1)\)表示三个相邻的顶点构成一个三角形,那么另外两个部分的顶点数分别为2和n-1。设f(2)=1,那么\(f(3)=1,f(4)=2,f(5)=5\)。结合递推式,不难发现f(n)等于h(n-2)。
5.在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数。
以其中一个点为基点,编号为0,然后按顺时针方向将其他点依次编号。那么与编号为0相连点的编号一定为奇数,否则,这两个编号间含有奇数个点,势必会有点被孤立,即在一条线段的两侧分别有一个孤立点,从而导致两线段相交。设选中的基点为A,与它连接的点为B,那么A和B将所有点分成两部分,一部分位于AB的左边,另一部分位于右边,然后分别求解即可。
于是\(f(n)=f(0) \times f(n-2) + f(2) \times f(n-4) + \cdots + f(n-2) \times f(0)\)。
\(f(0) \times f(n-2)\)表示编号0的点与编号1的点相连,此时位于它们右边的点的个数为0,而位于它们左边的点为2n-2。以此类推,\(f(0)=1,f(2)=1,f(4)=2\)。结合递推式不难发现f(2n)等于h(n)。
10 Prüfer序列
10.1 引入
prufer序列是一种将带标号的树用一个唯一的整数序列表示的方法。
prufer序列可以将一个带标号n个节点的树用[1,n]中的n-2个整数表示。你也可以理解为完全图的生成树与数列之间的双射。常用于组合计数问题中。
10.2 对树建立prufer序列
prufer序列是这样建立的:①每次选择一个编号最小的叶结点并删掉它;②在序列中记录下它连接到的那个节点,即它的父结点;③重复n-2次后只剩下两个结点,算法结束。
例如,这是一个7个结点的树的prufer序列的构造过程:
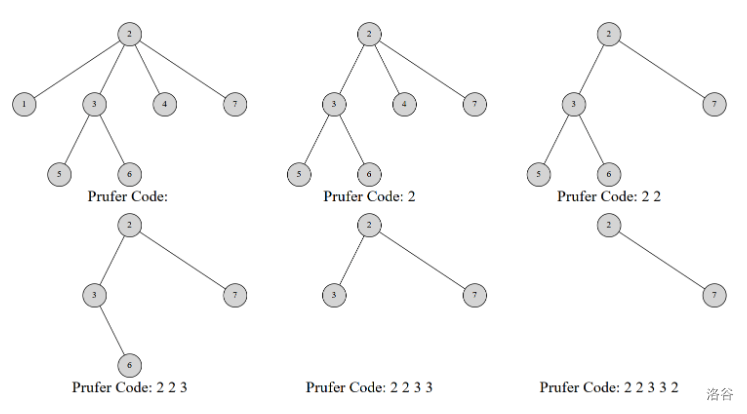
显然,维护一个小根堆,将叶子结点都丢入。每次从堆顶取出一个叶子结点,将其父结点编号加入序列,然后删去该叶子结点并减小其父结点的度。当父结点度为1时变为叶子结点,丢入小根堆。
vector<vector<int> > adj;
vector<int> pruefer_code() {
rg int n = adj.size();
set<int> leafs;
vector<int> degree(n);
vector<bool> killed(n, false);
for (rg int i = 0; i < n; i++) {
degree[i] = adj[i].size();
if (degree[i] == 1) leafs.insert(i);
}
vector<int> code(n - 2);
for (rg int i = 0; i < n - 2; i++) {
rg int leaf = *leafs.begin();
leafs.erase(leafs.begin());
killed[leaf] = true;
rg int v;
for (rg int j = 0; j < adj[leaf].size(); j++) {
rg int u = adj[leaf][j];
if (!killed[u]) v = u;
}
code[i] = v;
if (--degree[v] == 1) leafs.insert(v);
}
return code;
}
10.3 prufer序列的线性构造算法
初始时\(p\)的值为编号最小的叶子结点。
①将\(p\)的父结点\(f\)加入序列;②若删去\(p\)结点后\(f\)结点变为叶子结点,且\(f < p\),则此时可以将\(f\)作为新选择的叶子结点进行重复操作直到\(f > p\);③将\(p\)自增直到找到下一个未被删除的叶子结点。
int degree[N], fa[N], prufer[N];
int p, cnt;
inline void make_prufer() {
for (rg int i = 1; i <= n; i++) { //寻找编号最小的叶子结点
if (degree[i] == 1) {
p = i;
break;
}
}
rg int leaf = p; //leaf为当前选择要删去的叶子结点
while (cnt < n - 2) {
rg int f = fa[leaf];
prufer[++cnt] = f;
degree[f]--;
if (degree[f] == 1 && f < p) {
leaf = f;
} else {
p++;
while (degree[p] != 1) p++;
leaf = p;
}
}
}
10.4 prufer序列的性质
1.在构造完prufer序列后原树中会剩下两个结点,其中一个一定是编号最大的点n。
2.每个结点在序列中出现的次数是其度数减1(没有出现就是叶子结点)。
10.5 由prufer序列重建树
由性质2可知,每个结点的度数为prufer序列中出现次数+1。
①选择度数为1的最小的节点编号,与当前枚举到的prufer序列的点连接,然后同时减掉两个点的度。
②若度数变成1,则该结点也成为叶子结点。
③到最后剩下两个度数为1的点,其中一个是n。把他们连接。
10.6 线性时间重建树
初始时\(p\)的值为编号最小的未出现在序列中的结点。
①将\(p\)的父结点\(f\)设为prufer序列里尚未使用的第一个元素;②若删去\(p\)结点后\(f\)结点变为叶子结点且\(f < p\),则此时可以将\(f\)作为新选择的叶子结点进行重复操作直到\(f > p\)。③将\(p\)自增直到找到下一个还没删除的叶子结点。
int degree[N], fa[N], prufer[N];
int p, cnt;
inline void make_tree() {
for (rg int i = 1; i <= n; i++) degree[i] = 1;
for (rg int i = 1; i <= n - 2; i++) degree[prufer[i]]++; //度数为出现次数+1
for (rg int i = 1; i <= n; i++) { //找到编号最小的叶子结点
if (degree[i] == 1) {
p = i;
break;
}
}
rg int leaf = p; //leaf为当前选择要删去的叶子结点
while (cnt < n - 2) {
rg int f;
f = fa[leaf] = prufer[++cnt]; //当前结点的父亲为序列未使用的第一位
degree[f]--;
if (degree[f] == 1 && f < p) {
leaf = f;
} else {
p++;
while (degree[p] != 1) p++;
leaf = p;
}
}
fa[leaf] = n; //最后剩下两个结点,一个是n,把它们俩相连即可
}
10.7 prufer序列的应用
1.无向完全图的不同生成树数:
若该完全图有n个结点,则任意一个长度为n-2的prufer序列都可以重构出其一棵生成树,且各不相同。又因为prufer序列的值域在[1,n],故总数为\(n^{n-2}\)。
这就是Cayley公式。
2.n个点的无根树计数:
同上问题。
3.n个点的有根树计数:
对每棵无根树来说,每个点都可能是根,故总数为\(n^{n-2} \times n = n^{n-1}\)
4.n个点,每点度分别为\(d_i\)的无根树计数:
总排列数为\((n-2)!\),即\(A_{n-2}^{n-2}\)。
其中数字\(i\)出现了\(d_i-1\)次,故其重复的有\((d_i-1)!\)种排列,即\(A_{d_i-1}^{d_i-1}\)。
应当除去重复的,故总个数为\(\frac{(n-2)!}{\prod_{i=1}^{n}(d_i-1)!}\)。
11 BSGS
11.1 用处
求解高次同余方程
给定整数a,b,p,a、p互质,求满足\(a^x \equiv b \pmod p\)的最小非负整数x。
11.2 推导
由扩展欧拉定理:\(a^x \equiv a^{x \bmod \varphi(p)} \pmod p\),
可知\(a^x\)模p意义下的最小循环节为\(\varphi(p)\)。因为\(\varphi(p) < p\),故考虑\(x \in [0,p]\),必能找到最小整数x。
如果暴力枚举,时间是O(p)的。
令\(x=i \times m-j\),其中\(m=\lceil \sqrt p \rceil\),\(i \in [1,m]\),\(j \in [0,m-1]\),
则\(a^{i \times m - j} \equiv b \pmod p\),
即\((a^m)^i \equiv b \times a^j \pmod p\)。
①先枚举j,把\((b \times a^j, j)\)丢入哈希表,如果key重复,用更大的j替代旧的;
②再枚举i,计算\((a^m)^i\),到哈希表中查找是否有相等的key,找到第一个即结束。
则最小的\(x = i \times m - j\)
因为j与i的次数都是\(\sqrt p\)的,所以时间是\(O(\sqrt p)\)
11.3 模版
P3846 [TJOI2007] 可爱的质数/【模板】BSGS
#include<bits/stdc++.h>
#define rg register
#define qwq 0
using namespace std;
typedef long long ll;
inline ll bsgs(ll a, ll b, ll p) {
a %= p;
b %= p;
if (a == 0 && b != 0) return -1;
if (b == 1) return qwq;
rg ll m = ceil(sqrt(p)), t = b;
unordered_map<ll, ll> hash;
/*
unordered_map是一个将key和value关联起来的容器,它可以高效的根据单个key值查找对应的value。
key值应该是唯一的,key和value的数据类型可以不相同。
unordered_map存储元素时是没有顺序的,只是根据key的哈希值,将元素存在指定位置,所以根据key查找单个value时非常高效,平均可以在常数时间内完成。
unordered_map查询单个key的时候效率比map高,但是要查询某一范围内的key值时比map效率低。
可以使用[]操作符来访问key值对应的value值。
*/
hash[b] = 0;
for (rg int j = 1; j < m; j++) {
t = t * a % p; //求 b * a^j
hash[t] = j;
}
rg ll mi = 1;
for (rg int i = 1; i <= m; i++) {
mi = mi * a % p; //求 a^m
}
t = 1;
for (rg int i = 1; i <= m; i++) {
t = t * mi % p;
if (hash.count(t)) return i * m - hash[t];
}
return -1; //无解
}
int a, p, b;
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> p >> a >> b;
rg int res = bsgs(a, b, p);
if (res == -1) {
cout << "no solution\n";
} else {
cout << res << "\n";
}
return qwq;
}
例题1:[CSP-S2019] Emiya 家今天的饭
dp+容斥。
84 pts
我们发现一个方案不合法,有且只会有一个主要食材\(>\)总数的一半,所以我们不妨考虑容斥,用所有方案数量\(-\)不合法数量。
求解所有方案数量
所有方案数量很好求,做一个分组背包即可:
\(f[i][j]\)表示前i种烹饪方式,做了j道菜的方案数。
状态转移:
- 第i种烹饪方式不做菜:\(f[i][j] += f[i-1][j]\)
- 第i种烹饪方法做1道主要食材是k的菜:\(f[i][j] += f[i-1][j-1]\times a_{i,k}\)
所有方案数量\(=\displaystyle\sum_{j=1}^{n}f[n][j]\)
优化:我们可以\(O(nm)\)预处理\(s_i=a_{i,1}+a_{i,2}+\cdots+a_{i,m}\)。每个状态即可\(O(1)\)转移。
求解不合法数量
由于性质:所有不合法方案中有且只会有一个主要食材\(>\)总数的一半,我们称那个主要食材为越界食材,我们设越界食材为c。
所以我们不妨先用\(O(m)\)枚举c。那么我们可以把其他食材归结为符合条件的食材,我们便可以用一个维度来记录它选了多少。
设\(dp[i][j][k]\)为前i种烹饪方式,第c种(越界食材)选了j道,其他食材选了k道的方案数。
状态转移:
- 第i种烹饪方法不做菜:\(dp[i][j][k] += dp[i - 1][j][k]\),\(O(1)\)转移
- 选第c种(越界食材):\(dp[i][j][k] += dp[i - 1][j - 1][k]\times a_{i,c}(j>0)\),\(O(1)\)转移
- 选其他食材:\(dp[i][j][k] += \displaystyle\sum_{u=1,u!=c}^{m}dp[i-1][j][k-1]\times a_{i,u}\),\(O(m)\)转移
对答案的贡献:\(\sum dp[n][j][k](j>k)\)
优化:可以滚掉第一维。第三种转移最耗时,考虑用求解所有方案数量优化的思想:\(\displaystyle\sum_{u=1,u!=c}^{m}dp[i-1][j][k-1]\times a_{i,u}=dp[i-1][j][k-1]\times\displaystyle\sum_{u=1,u!=c}^{m}a_{i,u}=dp[i-1][j][k-1]\times(s_i-a_{i,c})\),我们就做到了\(O(1)\)转移。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 103, M = 2003, mod = 998244353;
int n, m;
int a[N][M];
int ans, res, ret;
int f[N][M], dp[N][N][N];
int s[N];
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m;
for (rg int i = 1; i <= n; i++) {
for (rg int j = 1; j <= m; j++) {
cin >> a[i][j];
s[i] = (s[i] + a[i][j]) % mod;
}
}
//求解合法数量
ans = 1;
for (rg int i = 1; i <= n; i++) {
ans = ans * (s[i] + 1) % mod;
}
ans--;
//求解不合法数量
for (rg int c = 1; c <= m; c++) {
memset(dp, 0, sizeof(dp));
ret = 0;
dp[0][0][0] = 1;
for (rg int i = 1; i <= n; i++) {
for (rg int j = 0; j <= i; j++) {
for (rg int k = 0; k <= i - j; k++) {
dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k]) % mod;
if (j > 0) dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j - 1][k] * a[i][c] % mod) % mod;
if (k > 0) dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k - 1] * (s[i] - a[i][c]) % mod) % mod;
}
}
}
for (rg int i = 1; i <= n; i++) {
for (rg int j = 0; j <= n - i; j++) {
if(i > j) res = (res + dp[n][i][j]) % mod;
}
}
}
cout << ((ans - res) % mod + mod) % mod << "\n";
return qwq;
}
100 pts
延续84pts的思想,求解不合法数量的\(O(n^3m)\)拖累了我们,我们考虑优化。
我们不关系具体越界食材与其他食材选了多少,只用保证越界食材数\(>\)其他食材数即为不合法状态,不妨把这两个的差作为一个维度,这样既可让dp状态降一维:
\(dp[i][j]\)表示前i种烹饪方法,越界食材数\(-\)其他食材数为j的方案数。
状态转移:
- 第i种烹饪方法不选:\(dp[i][j] += dp[i-1][j]\)
- 选越界食材:\(dp[i][j] += dp[i - 1][j-1]\times a_{i,c}\)
- 选其他食材:\(dp[i][j] += dp[i - 1][j+1]\times(s_i-a_{i,c})\)
答案贡献:\(\sum dp[n][j](j>0)\)
总时间复杂度\(O(n^2m)\)。
注意:做差可能为负数,我们把所有状态加一个n就可以了。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 103, M = 2003, mod = 998244353;
int n, m;
int a[N][M];
int ans, res, ret;
int f[N][M], dp[N][N + N];
int s[N];
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> n >> m;
for (rg int i = 1; i <= n; i++) {
for (rg int j = 1; j <= m; j++) {
cin >> a[i][j];
s[i] = (s[i] + a[i][j]) % mod;
}
}
//求解合法数量
ans = 1;
for (rg int i = 1; i <= n; i++) {
ans = ans * (s[i] + 1) % mod;
}
ans--;
//求解不合法数量
for (rg int c = 1; c <= m; c++) {
memset(dp, 0, sizeof(dp));
//dp[0][0] = 1;
dp[0][n] = 1;
for (rg int i = 1; i <= n; i++) {
for (rg int j = 0; j <= 2 * n; j++) {
dp[i][j] = (dp[i][j] + dp[i - 1][j]) % mod;
dp[i][j] = (dp[i][j] + dp[i - 1][j - 1] * a[i][c]) % mod;
dp[i][j] = (dp[i][j] + dp[i - 1][j + 1] * (s[i] - a[i][c]) % mod) % mod;
}
}
for (rg int i = n + 1; i <= 2 * n; i++) {
res = (res + dp[n][i]) % mod;
}
}
cout << ((ans - res) % mod + mod) % mod << "\n";
return qwq;
}
例题2:[cf869C] The Intriguing Obsession
因为两个同色小岛的距离要大于3,所以:
- 1.同色岛之间不能相连。
- 2.一个岛不能同时和两个颜色相同的岛相连。
那么只有三种连法:\(A-B,B-C,A-C\),而且这三种方法都是独立的,所以最终的答案就是这三种方法数相乘。
比如求A色岛与B色岛之间的方法数:
因为一个A色岛只能连一个B色岛,所以它的方法数就是:从a个岛里选0个的方法数\(\times\)从b个岛里选0个的方法数 \(\times\) 0个数的总排列数 \(+\) 从a个岛里选1个的方法数 \(\times\) 从b个岛里选1个的方法数 \(\times\) 1个数的总排列数 \(+\cdots +\) 从a个岛里选a个的方法数 \(\times\) 从b个岛里选a个的方法数 \(\times\) a个数的总排列数。( \(a \le b\) ),
也就是\(\displaystyle\sum_{i=0}^{a}C_a^i\times C_b^i \times i!\)。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 5003, mod = 998244353;
int f[N], g[N];
inline int qpow(int a, int b) {
rg int res = 1;
while (b) {
if (b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
inline void init() {
f[0] = g[0] = 1;
for (rg int i = 1; i < N; i++) {
f[i] = f[i - 1] * i % mod;
g[i] = g[i - 1] * qpow(i, mod - 2) % mod;
}
}
inline int C(int n, int m) {
return f[n] * g[m] % mod * g[n - m] % mod;
}
inline int solve(int a, int b) {
rg int res = 0;
for (rg int i = 0; i <= min(a, b); i++) {
res = (res + C(a, i) * C(b, i) % mod * f[i] % mod) % mod;
}
return res % mod;
}
int a, b, c;
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
init();
cin >> a >> b >> c;
cout << solve(a, b) * solve(a, c) % mod * solve(b, c) % mod << "\n";
return qwq;
}
例题3:Lengthening Sticks
首先计算出所有情况数,然后减去不合法的情况数即可。
对于总情况数:
枚举可发现规律:\(tot=\displaystyle\sum_{i=1}^{l+1}\frac{(i + 1)\cdot i}{2}\)。
对于不合法情况:
依次枚举三条边作为最长边的不合法情况,即最长边\(\ge\)其余两边之和。
注意特判即使加上全部l也比最长边小的情况,直接输出0。
#include<bits/stdc++.h>
#define rg register
#define qwq 0
#define int long long
using namespace std;
const int N = 3e5 + 3;
int a, b, c, l;
int tot;
inline int solve(int a, int b, int c) { //最长边为a
rg int d = b + c - a, nl = l, res = 0;
if (d > 0) {
nl -= d;
a += d;
}
for (rg int i = 0; i <= nl; i++) { //分给a的长度
/*for (rg int j = 0; j <= nl - i && b + c + j <= a + i; j++) {
res += j + 1;
}*/
rg int maxx = min(nl - i, a + i - b - c);
res += (maxx + 2) * (maxx + 1) / 2;
}
return res;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin >> a >> b >> c >> l;
rg int maxx = max(a, max(b, c));
if (maxx >= a + b + c - maxx + l) {
cout << 0 << "\n";
return qwq;
}
for (rg int i = 1; i <= l + 1; i++) {
tot += (i + 1) * i / 2;
}
cout << tot - solve(a, b, c) - solve(b, a, c) - solve(c, a, b) << "\n";
return qwq;
}