你觉得一个算法难,是因为你的大脑对未知世界的恐惧。——yxc
简单讲讲二分
- 二分是什么?
顾名思义:就是一分为二 (✓)
它是一种在有序数组中查找某一特定元素的搜索算法
- 怎么搜索呢?
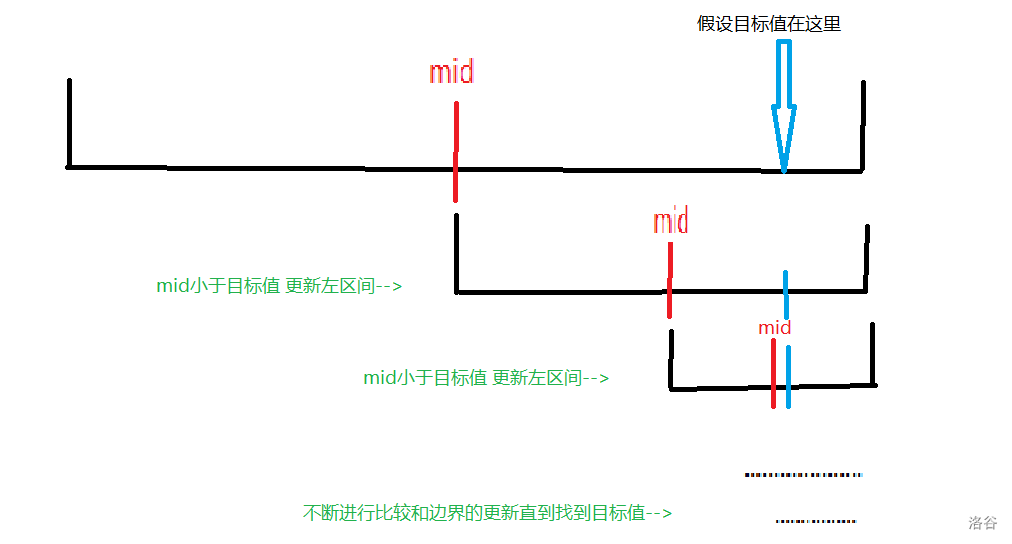
其实就是不断取中间位置的值(简称中间值) 和目标值v比较
如果中间值大于v 那么v肯定在中间值的左区间 那就更新右边界 继续取中间值进行比较
如果中间值小于v 那么v肯定在中间值的右区间 那就更新左边界 继续取中间值进行比较
然后一直如此循环直到找到目标值(目标值存在的前提下)
- 那么为什么要二分呢?
先举个例子:
在一组有序数列 2 3 4 5 6 7 8 9 23 34 45 56 67 中 找到56的位置
朴素做法:
从第一个依次向后枚举 判断是否为目标值 那么我们需要查询12次
二分大法:
第一次取第(1+13)/2=7个数即8 8<56
第二次取第(8+13)/2=10个数即34 34<56
第三次取第(10+13)/2=11个数即56 56==56
由上可见 二分需要比较的次数仅仅只有朴素做法的四分之一
这还仅仅是只有13个数的数列
那么当数据很大时 有成千上万个数时 二分查找的效率完虐朴素做法
这就是使用二分的原因
那么当数列中有多个重复目标值元素时 我们想找到第一个出现或者最后应该出现的位置时 该怎么办呢
我们只要对 mid的取值和边界的更新方式 稍微处理一下就能轻松应对啦!
这点很重要哦 下面给出模板
模板1、2都能用于查找无重复目标值
模板1:
查找上界
int max_vis(int l, int r, int v)
{
int mid;
while(l<r)
{
mid=(l+r+1)>>1;
if(b[mid]<=v) l=mid; //找到目标值时 左边界不断向右偏移
else r=mid-1; //
}
if(b[l]!=v) return -1; //如果不存在目标值返回-1
return l;
}
模板2:
查找下界
int min_vis(int l, int r, int v)
{
int mid;
while(l<r)
{
mid=(l+r)>>1;
if(b[mid]>=v) r=mid;//找到目标值时 右边界不断向左偏移
else l=mid+1;
}
if(b[l]!=v) return -1;//如果不存在目标值返回-1
return l;
}
注意:
-
mid取(l+r)>>1时 对应的边界处理:l=mid+1;r=mid;
-
mid取(l+r+1)>>1时 对应的边界处理:l=mid;r=mid-1;
(l+r)>>1取值靠向左边界 (l+r+1)>>1取值靠向右边界
mid取值要多加注意,否则会导致漏答案或死循环的结果。
自己可以试着模拟一下
可简记为:
在查找上界时,左边界不断向右偏移 寻找目标值的最大位置(l=mid),
到达最大位置时,右边界撞向左边界(r=mid-1),直到重合退出循环。
-->左偏移右撞
在查找下界时,右边界不断向左偏移 寻找目标值的最小位置(r=mid),
到达最小位置时,左边界撞向右边界(l=mid+1),直到重合退出循环。