1.题目

题目地址(419. 甲板上的战舰 - 力扣（LeetCode）)

https://leetcode.cn/problems/battleships-in-a-board/

题目描述

给你一个大小为 m x n 的矩阵 board 表示甲板，其中，每个单元格可以是一艘战舰 'X' 或者是一个空位 '.' ，返回在甲板 board 上放置的 战舰 的数量。

战舰 只能水平或者垂直放置在 board 上。换句话说，战舰只能按 1 x k（1 行，k 列）或 k x 1（k 行，1 列）的形状建造，其中 k 可以是任意大小。两艘战舰之间至少有一个水平或垂直的空位分隔 （即没有相邻的战舰）。

示例 1：

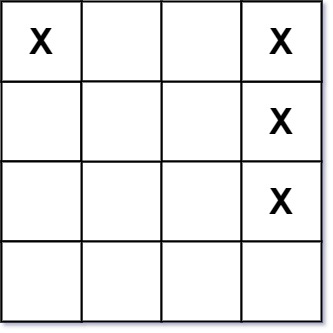
输入：board = [["X",".",".","X"],[".",".",".","X"],[".",".",".","X"]]
输出：2

示例 2：

输入：board = [["."]]
输出：0

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 是 '.' 或 'X'

进阶：你可以实现一次扫描算法，并只使用 O(1) 额外空间，并且不修改 board 的值来解决这个问题吗？

2.题解

2.1 遍历扫描(枚举-标记)

思路

由于已知战舰必然是在一行或者一列上, 且相邻两艘必定隔开一个空格, 我们找到一个X时,
就可以顺着row或者col往后进行遍历, 将所有相邻的X均变为'.'(进行标记),代表是一艘战舰, 这样之后就不会重复寻找了.

两种思路,没有本质区别
1.允许扫描多次，但空间只能 O(1)：每次遇到 X 的格子，则将 X 所在的战舰修改为 .，统计完答案后，再扫描一次，将 . 恢复为 X 即可；
2.扫描一次，但空间允许 O(m∗n)：使用一个与矩阵同等大小的辅助数组 vis 记录访问过的位置即可

代码

• 语言支持：C++

C++ Code:

class Solution {
public:
    int countBattleships(vector<vector<char>>& board) {
        int row = board.size(), col = board[0].size();
        int ans = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (board[i][j] == 'X') {
                    for (int k = i + 1; k < row && board[k][j] == 'X'; k++) {
                        board[k][j] = '.';
                    }
                    for (int k = j + 1; k < col && board[i][k] == 'X'; k++) {
                        board[i][k] = '.';
                    }
                    ans++;
                }
            }
        }
        return ans;
    }
};

复杂度分析

令 n 为数组长度。

• 时间复杂度：\(O(m × n × max(m,n))\)
• 空间复杂度：\(O(1))\)

2.2 去重判断

思路

思考上述两种做法，我们本质 都是在战舰的首个格子进行计数，并将该战舰的所有格子进行处理，同时使用去重手段（原数组标记 或 使用辅助数组）来防止该战舰在后面遍历中被重复计数。
如果我们能够找到某种规律，直接判断出某个 X 格子是否为战舰开头，则不再需要其他去重手段。

我们对于一个战舰开头, 其左方和上方必然不可能是'X', 如果是则不为战舰开头(注意位于i == 0 和 j == 0 的特殊情况, 这是没有左方和上方的, 判断一下即可)

代码

class Solution {
public:
    int countBattleships(vector<vector<char>>& board) {
        int row = board.size(), col = board[0].size();
        int ans = 0;
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if(i > 0 && board[i-1][j] == 'X') continue;
                if(j > 0 && board[i][j-1] == 'X') continue;
                if(board[i][j] == 'X') ans++;
            }
        }
        return ans;
    }
};

复杂度分析

令 n 为数组长度。

• 时间复杂度：\(O(m × n)\)
• 空间复杂度：\(O(1))\)